Contoh soal kesebangunan dan kekongruenan segitiga – Menjelajahi dunia geometri, kita akan menemukan konsep menarik tentang kesebangunan dan kekongruenan segitiga. Kedua konsep ini sangat penting dalam memahami bentuk dan ukuran objek di sekitar kita. Kesebangunan dan kekongruenan segitiga memiliki aplikasi luas dalam berbagai bidang, mulai dari arsitektur hingga teknik sipil. Dalam artikel ini, kita akan mempelajari contoh soal yang akan membantu Anda memahami dan menguasai konsep-konsep penting ini.
Melalui contoh soal yang disajikan, Anda akan diajak untuk menganalisis sifat-sifat segitiga, mengidentifikasi syarat kesebangunan dan kekongruenan, serta menerapkan konsep tersebut dalam menyelesaikan berbagai permasalahan geometri. Dengan memahami konsep ini, Anda akan lebih mudah dalam memecahkan soal-soal yang terkait dengan bentuk dan ukuran segitiga.
Pengertian Kesebangunan dan Kekongruenan Segitiga
Dalam geometri, kita mengenal dua konsep penting yang berkaitan dengan bentuk dan ukuran, yaitu kesebangunan dan kekongruenan. Kedua konsep ini sangat berguna untuk menganalisis dan membandingkan bentuk geometri, khususnya segitiga.
Kesebangunan Segitiga
Kesebangunan segitiga adalah konsep yang menggambarkan dua segitiga memiliki bentuk yang sama, namun ukurannya berbeda. Dua segitiga dikatakan sebangun jika memenuhi syarat-syarat berikut:
- Sudut-sudut yang bersesuaian sama besar.
- Sisi-sisi yang bersesuaian sebanding.
Contoh ilustrasi: Bayangkan dua segitiga, satu besar dan satu kecil. Kedua segitiga ini memiliki sudut-sudut yang sama besar, tetapi sisi-sisi segitiga besar lebih panjang daripada sisi-sisi segitiga kecil. Kedua segitiga ini dikatakan sebangun.
Kekongruenan Segitiga
Kekongruenan segitiga adalah konsep yang menggambarkan dua segitiga memiliki bentuk dan ukuran yang sama. Dua segitiga dikatakan kongruen jika memenuhi syarat-syarat berikut:
- Sudut-sudut yang bersesuaian sama besar.
- Sisi-sisi yang bersesuaian sama panjang.
Contoh ilustrasi: Bayangkan dua segitiga yang memiliki bentuk dan ukuran yang sama persis. Kedua segitiga ini dikatakan kongruen. Kita dapat memindahkan salah satu segitiga dan menumpangkannya tepat di atas segitiga lainnya, sehingga kedua segitiga tersebut akan saling menutupi sempurna.
Perbandingan Kesebangunan dan Kekongruenan Segitiga
| Ciri | Kesebangunan | Kekongruenan |
|---|---|---|
| Bentuk | Sama | Sama |
| Ukuran | Berbeda | Sama |
| Syarat | Sudut-sudut yang bersesuaian sama besar, sisi-sisi yang bersesuaian sebanding | Sudut-sudut yang bersesuaian sama besar, sisi-sisi yang bersesuaian sama panjang |
| Contoh | Dua segitiga dengan bentuk yang sama, tetapi satu lebih besar dari yang lain | Dua segitiga yang memiliki bentuk dan ukuran yang sama persis |
Syarat Kesebangunan Segitiga
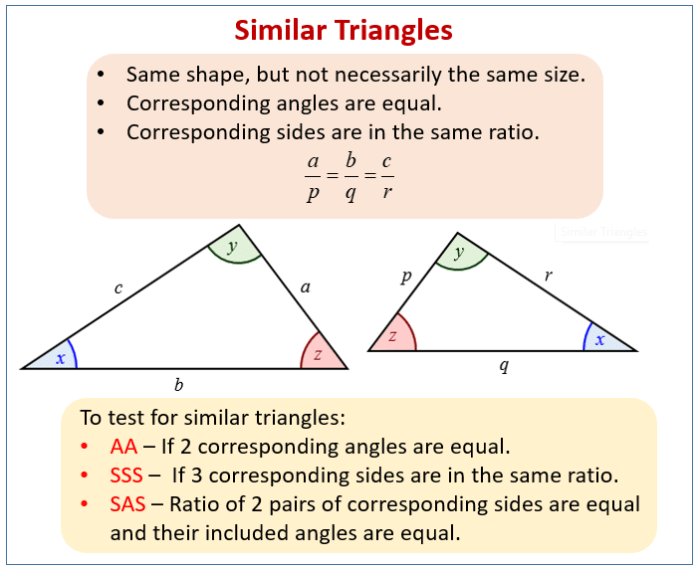
Kesebangunan merupakan konsep penting dalam geometri yang berkaitan dengan bentuk dan ukuran. Dua bangun geometri dikatakan sebangun jika bentuknya sama tetapi ukurannya berbeda. Dalam segitiga, terdapat beberapa syarat yang harus dipenuhi agar dua segitiga dapat dikatakan sebangun. Syarat-syarat tersebut memudahkan kita dalam menentukan apakah dua segitiga memiliki bentuk yang sama, meskipun ukurannya berbeda.
Syarat Kesebangunan Segitiga Berdasarkan Perbandingan Sisi
Dua segitiga dikatakan sebangun jika perbandingan sisi-sisi yang bersesuaian sama.
- Sisi-sisi yang bersesuaian adalah sisi-sisi yang berada pada posisi yang sama pada kedua segitiga. Misalnya, sisi terpanjang pada segitiga pertama akan bersesuaian dengan sisi terpanjang pada segitiga kedua.
- Perbandingan sisi-sisi yang bersesuaian harus sama untuk semua sisi.
Contoh Soal dan Penyelesaian Kesebangunan Segitiga Berdasarkan Perbandingan Sisi
Misalkan terdapat dua segitiga, yaitu segitiga ABC dan segitiga DEF. Diketahui bahwa panjang sisi AB = 6 cm, BC = 8 cm, dan AC = 10 cm. Panjang sisi DE = 9 cm, EF = 12 cm, dan DF = 15 cm. Apakah segitiga ABC dan segitiga DEF sebangun?
Untuk membuktikan kesebangunan, kita perlu memeriksa perbandingan sisi-sisi yang bersesuaian.
Perbandingan sisi AB dan DE: AB/DE = 6/9 = 2/3.
Perbandingan sisi BC dan EF: BC/EF = 8/12 = 2/3.
Perbandingan sisi AC dan DF: AC/DF = 10/15 = 2/3.
Terlihat bahwa perbandingan sisi-sisi yang bersesuaian sama, yaitu 2/3. Oleh karena itu, segitiga ABC dan segitiga DEF sebangun.
Syarat Kesebangunan Segitiga Berdasarkan Kesamaan Sudut
Dua segitiga dikatakan sebangun jika sudut-sudut yang bersesuaian sama besar.
- Sudut-sudut yang bersesuaian adalah sudut-sudut yang berada pada posisi yang sama pada kedua segitiga. Misalnya, sudut A pada segitiga pertama akan bersesuaian dengan sudut D pada segitiga kedua.
- Semua sudut yang bersesuaian harus sama besar.
Contoh Soal dan Penyelesaian Kesebangunan Segitiga Berdasarkan Kesamaan Sudut, Contoh soal kesebangunan dan kekongruenan segitiga
Misalkan terdapat dua segitiga, yaitu segitiga PQR dan segitiga XYZ. Diketahui bahwa besar sudut P = 60 derajat, sudut Q = 80 derajat, dan sudut R = 40 derajat. Besar sudut X = 60 derajat, sudut Y = 80 derajat, dan sudut Z = 40 derajat. Apakah segitiga PQR dan segitiga XYZ sebangun?
Untuk membuktikan kesebangunan, kita perlu memeriksa kesamaan sudut-sudut yang bersesuaian.
Sudut P = sudut X = 60 derajat.
Sudut Q = sudut Y = 80 derajat.
Sudut R = sudut Z = 40 derajat.
Terlihat bahwa semua sudut yang bersesuaian sama besar. Oleh karena itu, segitiga PQR dan segitiga XYZ sebangun.
Syarat Kekongruenan Segitiga: Contoh Soal Kesebangunan Dan Kekongruenan Segitiga
Dalam geometri, dua bangun dikatakan kongruen jika keduanya memiliki bentuk dan ukuran yang sama. Untuk segitiga, ada beberapa syarat yang harus dipenuhi agar dua segitiga dikatakan kongruen. Syarat-syarat ini membantu kita untuk menentukan apakah dua segitiga memiliki bentuk dan ukuran yang sama tanpa harus mengukur semua sisi dan sudutnya.
Syarat Kekongruenan Segitiga Berdasarkan Sisi-Sisi-Sisi (SSS)
Dua segitiga dikatakan kongruen berdasarkan SSS jika ketiga sisi pada segitiga pertama sama panjang dengan ketiga sisi pada segitiga kedua.
- Jika segitiga ABC memiliki sisi AB, BC, dan AC yang sama panjang dengan sisi DE, EF, dan DF pada segitiga DEF, maka segitiga ABC kongruen dengan segitiga DEF.
Syarat Kekongruenan Segitiga Berdasarkan Sisi-Sudut-Sisi (SAS)
Dua segitiga dikatakan kongruen berdasarkan SAS jika dua sisi dan sudut yang diapit oleh kedua sisi tersebut pada segitiga pertama sama panjang dan besar dengan dua sisi dan sudut yang diapit oleh kedua sisi tersebut pada segitiga kedua.
- Jika segitiga ABC memiliki sisi AB dan BC yang sama panjang dengan sisi DE dan EF pada segitiga DEF, serta sudut ABC sama besar dengan sudut DEF, maka segitiga ABC kongruen dengan segitiga DEF.
Syarat Kekongruenan Segitiga Berdasarkan Sudut-Sisi-Sudut (ASA)
Dua segitiga dikatakan kongruen berdasarkan ASA jika dua sudut dan sisi yang diapit oleh kedua sudut tersebut pada segitiga pertama sama besar dan panjang dengan dua sudut dan sisi yang diapit oleh kedua sudut tersebut pada segitiga kedua.
- Jika segitiga ABC memiliki sudut A dan sudut B yang sama besar dengan sudut D dan sudut E pada segitiga DEF, serta sisi AB sama panjang dengan sisi DE, maka segitiga ABC kongruen dengan segitiga DEF.
Contoh Soal dan Penyelesaian Kekongruenan Segitiga Berdasarkan SSS
Perhatikan segitiga ABC dan segitiga DEF berikut.
Diketahui: AB = DE, BC = EF, dan AC = DF.
Buktikan: Segitiga ABC kongruen dengan segitiga DEF.
Penyelesaian:
Karena AB = DE, BC = EF, dan AC = DF, maka berdasarkan syarat SSS, segitiga ABC kongruen dengan segitiga DEF.
Contoh Soal dan Penyelesaian Kekongruenan Segitiga Berdasarkan SAS
Perhatikan segitiga ABC dan segitiga DEF berikut.
Diketahui: AB = DE, BC = EF, dan sudut ABC = sudut DEF.
Buktikan: Segitiga ABC kongruen dengan segitiga DEF.
Penyelesaian:
Karena AB = DE, BC = EF, dan sudut ABC = sudut DEF, maka berdasarkan syarat SAS, segitiga ABC kongruen dengan segitiga DEF.
Contoh Soal dan Penyelesaian Kekongruenan Segitiga Berdasarkan ASA
Perhatikan segitiga ABC dan segitiga DEF berikut.
Diketahui: sudut A = sudut D, sudut B = sudut E, dan AB = DE.
Buktikan: Segitiga ABC kongruen dengan segitiga DEF.
Penyelesaian:
Karena sudut A = sudut D, sudut B = sudut E, dan AB = DE, maka berdasarkan syarat ASA, segitiga ABC kongruen dengan segitiga DEF.
Penerapan Kesebangunan dan Kekongruenan Segitiga
Konsep kesebangunan dan kekongruenan segitiga ternyata punya peran penting dalam berbagai bidang kehidupan, lho. Mulai dari arsitektur hingga seni, kedua konsep ini berperan dalam menciptakan desain yang estetis dan fungsional. Yuk, kita telusuri lebih dalam!
Penerapan Kesebangunan Segitiga dalam Kehidupan Sehari-hari
Kesebangunan segitiga membantu kita dalam menentukan ukuran dan bentuk suatu objek tanpa harus mengukur langsung. Contohnya, saat kamu ingin mengetahui tinggi pohon tanpa harus memanjatnya, kamu bisa menggunakan konsep kesebangunan segitiga. Bayangkan, kamu berdiri di dekat pohon, lalu kamu ukur panjang bayanganmu dan panjang bayangan pohon. Karena matahari bersinar dengan sudut yang sama, maka segitiga yang dibentuk oleh kamu, bayanganmu, dan pohon dengan bayangannya akan sebangun. Dengan menggunakan perbandingan sisi yang bersesuaian, kamu bisa menghitung tinggi pohon dengan mudah.
Penerapan Kekongruenan Segitiga dalam Kehidupan Sehari-hari
Kekongruenan segitiga, di sisi lain, membantu kita dalam memastikan bahwa dua objek memiliki bentuk dan ukuran yang sama persis. Contohnya, dalam pembuatan puzzle, setiap potongan puzzle harus memiliki bentuk dan ukuran yang sama persis agar dapat disusun dengan tepat. Konsep kekongruenan segitiga memastikan bahwa setiap potongan puzzle memiliki bentuk dan ukuran yang identik, sehingga dapat disusun dengan sempurna.
Penerapan Kesebangunan dan Kekongruenan Segitiga dalam Berbagai Bidang
| Bidang | Penerapan Kesebangunan | Penerapan Kekongruenan | |
|---|---|---|---|
| Arsitektur | – Perencanaan desain bangunan dengan skala yang sesuai. – Menghitung ukuran dan bentuk atap bangunan dengan akurat. |
– Pembuatan struktur bangunan dengan bentuk dan ukuran yang sama persis. – Pemasangan jendela dan pintu dengan ukuran yang sama. |
|
| Teknik Sipil | – Perencanaan pembangunan jembatan dan gedung bertingkat dengan skala yang sesuai. – Menghitung ukuran dan bentuk struktur penyangga bangunan dengan akurat. |
– Pembuatan beton cor dengan bentuk dan ukuran yang sama. | – Pemasangan balok penyangga dengan ukuran yang sama. |
| Seni | – Pembuatan lukisan dengan perspektif yang tepat. – Menghitung ukuran dan bentuk objek dalam karya seni. |
– Pembuatan patung dengan bentuk dan ukuran yang sama. – Pembuatan mozaik dengan bentuk dan ukuran yang sama. |
Soal Latihan Kesebangunan dan Kekongruenan Segitiga
Pada materi geometri, kita mengenal konsep kesebangunan dan kekongruenan pada bangun datar, khususnya segitiga. Kedua konsep ini memiliki perbedaan yang mendasar. Kesebangunan menunjukkan dua bangun memiliki bentuk yang sama tetapi ukuran yang berbeda, sedangkan kekongruenan menunjukkan dua bangun memiliki bentuk dan ukuran yang sama. Untuk memahami konsep ini lebih dalam, berikut beberapa soal latihan yang dapat kamu kerjakan.
Soal Latihan Kesebangunan Segitiga
Berikut adalah 5 soal latihan kesebangunan segitiga dengan berbagai tingkat kesulitan. Soal-soal ini dirancang untuk menguji pemahamanmu tentang konsep kesebangunan, kriteria kesebangunan, dan cara menentukan panjang sisi yang belum diketahui.
-
Perhatikan gambar dua segitiga berikut:
Segitiga ABC dan segitiga DEF memiliki sudut-sudut yang sama besar. Sudut A = sudut D, sudut B = sudut E, dan sudut C = sudut F. Jika diketahui panjang AB = 6 cm, BC = 8 cm, dan DE = 9 cm, tentukan panjang EF.
Pembahasan: Karena kedua segitiga memiliki sudut-sudut yang sama besar, maka segitiga ABC dan segitiga DEF sebangun. Perbandingan sisi-sisi yang bersesuaian pada segitiga sebangun selalu sama. Oleh karena itu, kita dapat menentukan panjang EF dengan perbandingan berikut:
AB/DE = BC/EF
6/9 = 8/EF
EF = 9 * 8 / 6 = 12 cm
Jadi, panjang EF adalah 12 cm.
-
Perhatikan gambar dua segitiga berikut:
Segitiga PQR dan segitiga STU memiliki sisi-sisi yang sebanding. Panjang PQ = 4 cm, QR = 6 cm, PR = 8 cm, ST = 6 cm, dan SU = 9 cm. Apakah kedua segitiga tersebut sebangun? Jelaskan jawabanmu.
Pembahasan: Untuk menentukan apakah kedua segitiga sebangun, kita perlu memeriksa perbandingan sisi-sisi yang bersesuaian. Perbandingan sisi PQ/ST = 4/6 = 2/3. Perbandingan sisi QR/SU = 6/9 = 2/3. Perbandingan sisi PR/TU = 8/12 = 2/3. Karena semua perbandingan sisi-sisi yang bersesuaian sama, maka segitiga PQR dan segitiga STU sebangun.
-
Perhatikan gambar segitiga ABC berikut:
Garis DE sejajar dengan sisi BC. Panjang AD = 4 cm, DB = 6 cm, dan AC = 10 cm. Tentukan panjang AE.
Pembahasan: Karena DE sejajar dengan BC, maka segitiga ADE dan segitiga ABC sebangun. Perbandingan sisi-sisi yang bersesuaian pada segitiga sebangun selalu sama. Oleh karena itu, kita dapat menentukan panjang AE dengan perbandingan berikut:
AD/AB = AE/AC
4/10 = AE/10
AE = 4 cm
Contoh soal kesebangunan dan kekongruenan segitiga memang sering muncul di ujian. Soal-soal ini biasanya melibatkan perbandingan sisi dan sudut, serta pemahaman tentang sifat-sifat kedua konsep tersebut. Tapi, tahukah kamu kalau ada topik lain yang juga melibatkan konsep perbandingan, yaitu hereditas?
Contoh soal hereditas menguji pemahaman kita tentang pewarisan sifat dari orang tua ke anak, yang juga melibatkan perbandingan rasio gen dan fenotip. Kembali ke topik kesebangunan dan kekongruenan segitiga, soal-soal ini biasanya melibatkan rumus dan aplikasi langsung dari teorema, seperti teorema Pythagoras dan teorema kesebangunan.
Jadi, panjang AE adalah 4 cm.
-
Perhatikan gambar dua segitiga berikut:
Segitiga KLM dan segitiga XYZ memiliki sudut-sudut yang sama besar. Sudut K = sudut X, sudut L = sudut Y, dan sudut M = sudut Z. Jika diketahui panjang KL = 5 cm, LM = 7 cm, dan XY = 10 cm, tentukan keliling segitiga XYZ.
Pembahasan: Karena kedua segitiga memiliki sudut-sudut yang sama besar, maka segitiga KLM dan segitiga XYZ sebangun. Perbandingan sisi-sisi yang bersesuaian pada segitiga sebangun selalu sama. Oleh karena itu, kita dapat menentukan panjang sisi-sisi segitiga XYZ dengan perbandingan berikut:
KL/XY = LM/YZ = KM/XZ
5/10 = 7/YZ = KM/XZ
YZ = 14 cm dan XZ = 10 cm
Keliling segitiga XYZ = XY + YZ + XZ = 10 + 14 + 10 = 34 cm.
-
Perhatikan gambar dua segitiga berikut:
Segitiga ABC dan segitiga DEF memiliki dua sudut yang sama besar. Sudut A = sudut D dan sudut B = sudut E. Jika diketahui panjang AB = 8 cm, BC = 10 cm, dan DE = 12 cm, tentukan panjang EF.
Pembahasan: Karena kedua segitiga memiliki dua sudut yang sama besar, maka segitiga ABC dan segitiga DEF sebangun berdasarkan kriteria sudut-sudut yang sama besar. Perbandingan sisi-sisi yang bersesuaian pada segitiga sebangun selalu sama. Oleh karena itu, kita dapat menentukan panjang EF dengan perbandingan berikut:
AB/DE = BC/EF
8/12 = 10/EF
EF = 12 * 10 / 8 = 15 cm
Jadi, panjang EF adalah 15 cm.
Soal Latihan Kekongruenan Segitiga
Berikut adalah 5 soal latihan kekongruenan segitiga dengan berbagai tingkat kesulitan. Soal-soal ini dirancang untuk menguji pemahamanmu tentang konsep kekongruenan, kriteria kekongruenan, dan cara menentukan apakah dua segitiga kongruen.
-
Perhatikan gambar dua segitiga berikut:
Segitiga ABC dan segitiga DEF memiliki ketiga sisi yang sama panjang. Panjang AB = DE, BC = EF, dan AC = DF. Apakah kedua segitiga tersebut kongruen? Jelaskan jawabanmu.
Pembahasan: Ya, kedua segitiga tersebut kongruen. Karena ketiga sisi pada kedua segitiga memiliki panjang yang sama, maka kedua segitiga tersebut kongruen berdasarkan kriteria sisi-sisi-sisi (SSS).
-
Perhatikan gambar dua segitiga berikut:
Segitiga PQR dan segitiga STU memiliki dua sisi dan sudut apit yang sama besar. Panjang PQ = ST, QR = SU, dan sudut Q = sudut S. Apakah kedua segitiga tersebut kongruen? Jelaskan jawabanmu.
Pembahasan: Ya, kedua segitiga tersebut kongruen. Karena kedua segitiga memiliki dua sisi dan sudut apit yang sama besar, maka kedua segitiga tersebut kongruen berdasarkan kriteria sisi-sudut-sisi (SAS).
-
Perhatikan gambar dua segitiga berikut:
Segitiga KLM dan segitiga XYZ memiliki dua sudut dan sisi yang bersesuaian sama besar. Sudut K = sudut X, sudut L = sudut Y, dan panjang KL = XY. Apakah kedua segitiga tersebut kongruen? Jelaskan jawabanmu.
Pembahasan: Ya, kedua segitiga tersebut kongruen. Karena kedua segitiga memiliki dua sudut dan sisi yang bersesuaian sama besar, maka kedua segitiga tersebut kongruen berdasarkan kriteria sudut-sisi-sudut (SAS).
-
Perhatikan gambar dua segitiga berikut:
Segitiga ABC dan segitiga DEF memiliki sudut siku-siku di sudut B dan sudut E. Panjang AB = DE dan BC = EF. Apakah kedua segitiga tersebut kongruen? Jelaskan jawabanmu.
Pembahasan: Ya, kedua segitiga tersebut kongruen. Karena kedua segitiga memiliki sudut siku-siku, satu sisi yang bersesuaian sama panjang, dan sisi miring yang bersesuaian sama panjang, maka kedua segitiga tersebut kongruen berdasarkan kriteria sisi-miring-sisi (SMS).
-
Perhatikan gambar dua segitiga berikut:
Segitiga PQR dan segitiga STU memiliki tiga sudut yang sama besar. Sudut P = sudut S, sudut Q = sudut T, dan sudut R = sudut U. Apakah kedua segitiga tersebut kongruen? Jelaskan jawabanmu.
Pembahasan: Tidak, kedua segitiga tersebut tidak selalu kongruen. Karena ketiga sudut pada kedua segitiga memiliki besar yang sama, maka kedua segitiga tersebut sebangun, tetapi tidak selalu kongruen. Untuk menentukan kekongruenan, dibutuhkan informasi tambahan seperti panjang sisi yang bersesuaian.
Rumus dan Teorema Kesebangunan dan Kekongruenan Segitiga
Dalam geometri, kesebangunan dan kekongruenan merupakan konsep penting untuk memahami hubungan antar bangun geometri, khususnya segitiga. Kesebangunan merujuk pada bentuk yang sama, sedangkan kekongruenan mengacu pada bentuk dan ukuran yang sama. Artikel ini akan membahas rumus dan teorema yang berkaitan dengan kedua konsep ini.
Kesebangunan Segitiga
Dua segitiga dikatakan sebangun jika sudut-sudut yang bersesuaian sama besar dan sisi-sisi yang bersesuaian sebanding. Berikut adalah rumus dan teorema yang terkait dengan kesebangunan segitiga:
- Sudut-Sudut-Sudut (SSS): Jika dua sudut dari satu segitiga sama besar dengan dua sudut dari segitiga lainnya, maka kedua segitiga tersebut sebangun.
- Sisi-Sisi-Sisi (SSS): Jika ketiga sisi dari satu segitiga sebanding dengan ketiga sisi dari segitiga lainnya, maka kedua segitiga tersebut sebangun.
- Sisi-Sudut-Sisi (SAS): Jika dua sisi dari satu segitiga sebanding dengan dua sisi dari segitiga lainnya, dan sudut yang diapit oleh kedua sisi tersebut sama besar, maka kedua segitiga tersebut sebangun.
Kekongruenan Segitiga
Dua segitiga dikatakan kongruen jika ketiga sisinya sama panjang dan ketiga sudutnya sama besar. Berikut adalah rumus dan teorema yang terkait dengan kekongruenan segitiga:
- Sisi-Sisi-Sisi (SSS): Jika ketiga sisi dari satu segitiga sama panjang dengan ketiga sisi dari segitiga lainnya, maka kedua segitiga tersebut kongruen.
- Sisi-Sudut-Sisi (SAS): Jika dua sisi dari satu segitiga sama panjang dengan dua sisi dari segitiga lainnya, dan sudut yang diapit oleh kedua sisi tersebut sama besar, maka kedua segitiga tersebut kongruen.
- Sudut-Sisi-Sudut (ASA): Jika dua sudut dari satu segitiga sama besar dengan dua sudut dari segitiga lainnya, dan sisi yang diapit oleh kedua sudut tersebut sama panjang, maka kedua segitiga tersebut kongruen.
- Sudut-Sudut-Sisi (AAS): Jika dua sudut dari satu segitiga sama besar dengan dua sudut dari segitiga lainnya, dan sisi yang tidak diapit oleh kedua sudut tersebut sama panjang, maka kedua segitiga tersebut kongruen.
Contoh Soal dan Penyelesaian
Berikut adalah contoh soal dan penyelesaian yang menggunakan rumus dan teorema kesebangunan dan kekongruenan segitiga:
Soal: Diketahui segitiga ABC dan segitiga DEF dengan ∠A = ∠D, ∠B = ∠E, dan AB = 2DE. Apakah segitiga ABC dan segitiga DEF sebangun? Jika ya, tentukan perbandingan sisi-sisi yang bersesuaian.
Penyelesaian: Karena ∠A = ∠D dan ∠B = ∠E, maka segitiga ABC dan segitiga DEF sebangun berdasarkan teorema sudut-sudut-sudut (SSS). Perbandingan sisi-sisi yang bersesuaian adalah AB:DE = BC:EF = AC:DF. Karena AB = 2DE, maka perbandingan sisi-sisi yang bersesuaian adalah 2:1.
Perbedaan Kesebangunan dan Kekongruenan Segitiga
Dalam geometri, kita mengenal dua konsep penting yang berkaitan dengan bentuk dan ukuran segitiga: kesebangunan dan kekongruenan. Meskipun keduanya berhubungan dengan kesamaan bentuk, terdapat perbedaan mendasar yang perlu dipahami.
Perbedaan Utama Kesebangunan dan Kekongruenan
Perbedaan utama antara kesebangunan dan kekongruenan terletak pada aspek ukuran. Segitiga yang sebangun memiliki bentuk yang sama tetapi ukurannya berbeda, sedangkan segitiga yang kongruen memiliki bentuk dan ukuran yang sama.
Tabel Perbedaan Kesebangunan dan Kekongruenan
| Kriteria | Kesebangunan | Kekongruenan |
|---|---|---|
| Bentuk | Sama | Sama |
| Ukuran | Berbeda | Sama |
| Sudut | Sama besar | Sama besar |
| Sisi | Sebanding | Sama panjang |
| Syarat | Sudut-sudut yang bersesuaian sama besar, sisi-sisi yang bersesuaian sebanding | Sisi-sisi yang bersesuaian sama panjang, sudut-sudut yang bersesuaian sama besar |
Contoh Ilustrasi
Bayangkan sebuah segitiga kecil dan segitiga besar. Kedua segitiga memiliki bentuk yang sama, tetapi ukurannya berbeda. Segitiga kecil adalah versi yang diperkecil dari segitiga besar. Dalam hal ini, kedua segitiga tersebut sebangun.
Sekarang, bayangkan dua segitiga yang memiliki bentuk dan ukuran yang sama persis. Kedua segitiga tersebut dapat saling tumpang tindih dengan sempurna. Dalam hal ini, kedua segitiga tersebut kongruen.
Contoh Soal Kesebangunan dan Kekongruenan Segitiga
Kesebangunan dan kekongruenan merupakan konsep penting dalam geometri yang mempelajari hubungan antara bentuk dan ukuran dua atau lebih bangun geometri. Dua bangun dikatakan sebangun jika memiliki bentuk yang sama tetapi ukuran yang berbeda, sedangkan dua bangun dikatakan kongruen jika memiliki bentuk dan ukuran yang sama. Dalam artikel ini, kita akan membahas contoh soal kesebangunan dan kekongruenan segitiga dengan tingkat kesulitan yang berbeda.
Contoh Soal Kesebangunan Segitiga
Berikut adalah beberapa contoh soal kesebangunan segitiga:
-
Soal 1 (Tingkat Kesulitan: Mudah)
Perhatikan gambar segitiga ABC dan segitiga DEF di bawah ini:
Gambarlah ilustrasi segitiga ABC dan segitiga DEF dengan sudut-sudut yang sama, dan perbandingan sisi-sisi yang sama.
Jika diketahui bahwa ∠A = ∠D, ∠B = ∠E, dan ∠C = ∠F, serta AB = 4 cm, BC = 6 cm, dan DE = 2 cm, tentukan panjang sisi DF dan EF!
Penyelesaian:
Karena ∠A = ∠D, ∠B = ∠E, dan ∠C = ∠F, maka segitiga ABC dan segitiga DEF sebangun. Perbandingan sisi-sisi yang bersesuaian pada segitiga sebangun adalah sama. Oleh karena itu, kita dapat menentukan panjang sisi DF dan EF sebagai berikut:
AB/DE = BC/EF = AC/DF
4/2 = 6/EF = AC/DF
EF = 3 cm
AC/DF = 4/2
AC = 2DF
Jadi, panjang sisi DF adalah 2 cm dan panjang sisi EF adalah 3 cm.
-
Soal 2 (Tingkat Kesulitan: Sedang)
Perhatikan gambar segitiga PQR dan segitiga STU di bawah ini:
Gambarlah ilustrasi segitiga PQR dan segitiga STU dengan sudut-sudut yang sama, dan perbandingan sisi-sisi yang sama.
Jika diketahui bahwa PQ = 8 cm, QR = 12 cm, dan ST = 4 cm, serta ∠P = ∠S dan ∠Q = ∠T, tentukan panjang sisi TU dan SU!
Penyelesaian:
Karena ∠P = ∠S dan ∠Q = ∠T, maka segitiga PQR dan segitiga STU sebangun. Perbandingan sisi-sisi yang bersesuaian pada segitiga sebangun adalah sama. Oleh karena itu, kita dapat menentukan panjang sisi TU dan SU sebagai berikut:
PQ/ST = QR/TU = PR/SU
8/4 = 12/TU = PR/SU
TU = 6 cm
PR/SU = 8/4
PR = 2SU
Jadi, panjang sisi TU adalah 6 cm dan panjang sisi SU adalah setengah dari panjang sisi PR.
-
Soal 3 (Tingkat Kesulitan: Sulit)
Perhatikan gambar trapesium ABCD di bawah ini:
Gambarlah ilustrasi trapesium ABCD dengan garis yang membagi trapesium menjadi dua segitiga, yaitu segitiga ABE dan segitiga CDE. Pastikan gambar menunjukkan bahwa garis tersebut sejajar dengan sisi AB dan CD.
Jika diketahui bahwa AB = 10 cm, CD = 6 cm, dan AE = 8 cm, tentukan panjang sisi DE dan BC!
Penyelesaian:
Karena garis BE sejajar dengan sisi AB dan CD, maka segitiga ABE dan segitiga CDE sebangun. Perbandingan sisi-sisi yang bersesuaian pada segitiga sebangun adalah sama. Oleh karena itu, kita dapat menentukan panjang sisi DE dan BC sebagai berikut:
AB/CD = AE/DE = BE/CE
10/6 = 8/DE = BE/CE
DE = 4,8 cm
BE/CE = 10/6
BE = (5/3)CE
BC = BE + CE = (5/3)CE + CE = (8/3)CE
Jadi, panjang sisi DE adalah 4,8 cm dan panjang sisi BC adalah (8/3) kali panjang sisi CE.
Contoh Soal Kekongruenan Segitiga
Berikut adalah beberapa contoh soal kekongruenan segitiga:
-
Soal 1 (Tingkat Kesulitan: Mudah)
Perhatikan gambar segitiga ABC dan segitiga DEF di bawah ini:
Gambarlah ilustrasi segitiga ABC dan segitiga DEF dengan sisi-sisi yang sama panjang, dan sudut-sudut yang sama besar.
Jika diketahui bahwa AB = DE, BC = EF, dan AC = DF, tentukan apakah segitiga ABC dan segitiga DEF kongruen!
Penyelesaian:
Karena AB = DE, BC = EF, dan AC = DF, maka segitiga ABC dan segitiga DEF kongruen berdasarkan kriteria sisi-sisi-sisi (SSS).
-
Soal 2 (Tingkat Kesulitan: Sedang)
Perhatikan gambar segitiga PQR dan segitiga STU di bawah ini:
Gambarlah ilustrasi segitiga PQR dan segitiga STU dengan dua sisi yang sama panjang, dan sudut apit yang sama besar.
Jika diketahui bahwa PQ = ST, QR = TU, dan ∠Q = ∠T, tentukan apakah segitiga PQR dan segitiga STU kongruen!
Penyelesaian:
Karena PQ = ST, QR = TU, dan ∠Q = ∠T, maka segitiga PQR dan segitiga STU kongruen berdasarkan kriteria sisi-sisi-sudut (SAS).
-
Soal 3 (Tingkat Kesulitan: Sulit)
Perhatikan gambar segitiga KLM dan segitiga XYZ di bawah ini:
Gambarlah ilustrasi segitiga KLM dan segitiga XYZ dengan dua sudut yang sama besar, dan sisi yang berhadapan dengan sudut yang sama besar juga sama panjang.
Jika diketahui bahwa ∠K = ∠X, ∠L = ∠Y, dan KL = XY, tentukan apakah segitiga KLM dan segitiga XYZ kongruen!
Penyelesaian:
Karena ∠K = ∠X, ∠L = ∠Y, dan KL = XY, maka segitiga KLM dan segitiga XYZ kongruen berdasarkan kriteria sudut-sudut-sisi (SAS).
Tips Mengerjakan Soal Kesebangunan dan Kekongruenan Segitiga
Materi kesebangunan dan kekongruenan segitiga merupakan materi penting dalam geometri yang sering muncul dalam ujian. Untuk menyelesaikan soal-soal terkait materi ini dengan mudah dan tepat, diperlukan pemahaman yang baik tentang konsep-konsep dasar dan penerapannya. Berikut ini beberapa tips yang dapat membantu kamu dalam mengerjakan soal kesebangunan dan kekongruenan segitiga:
Tips Mengerjakan Soal Kesebangunan Segitiga
Kesebangunan segitiga terjadi ketika dua segitiga memiliki bentuk yang sama, namun ukurannya berbeda. Untuk menentukan apakah dua segitiga sebangun, kamu dapat menggunakan beberapa kriteria, seperti perbandingan sisi-sisi, perbandingan sudut-sudut, atau kombinasi keduanya.
- Pahami konsep perbandingan sisi-sisi: Dua segitiga sebangun jika perbandingan sisi-sisi yang bersesuaian sama. Misalnya, jika sisi-sisi segitiga A adalah 3, 4, dan 5, dan sisi-sisi segitiga B adalah 6, 8, dan 10, maka kedua segitiga tersebut sebangun karena perbandingan sisi-sisi yang bersesuaian sama, yaitu 1:2.
- Pahami konsep perbandingan sudut-sudut: Dua segitiga sebangun jika sudut-sudut yang bersesuaian sama. Misalnya, jika sudut-sudut segitiga A adalah 60°, 80°, dan 40°, dan sudut-sudut segitiga B adalah 60°, 80°, dan 40°, maka kedua segitiga tersebut sebangun karena sudut-sudut yang bersesuaian sama.
- Gunakan teorema kesebangunan segitiga: Terdapat beberapa teorema kesebangunan segitiga, seperti teorema SSS (sisi-sisi-sisi), SAS (sisi-sudut-sisi), dan AA (sudut-sudut).
- Perhatikan skala: Perbandingan sisi-sisi yang bersesuaian pada segitiga sebangun disebut skala. Skala ini dapat digunakan untuk menentukan panjang sisi yang belum diketahui pada segitiga sebangun.
- Latih dengan contoh soal: Mengerjakan soal-soal latihan adalah cara terbaik untuk memahami konsep kesebangunan segitiga.
Tips Mengerjakan Soal Kekongruenan Segitiga
Kekongruenan segitiga terjadi ketika dua segitiga memiliki bentuk dan ukuran yang sama. Untuk menentukan apakah dua segitiga kongruen, kamu dapat menggunakan beberapa kriteria, seperti perbandingan sisi-sisi, perbandingan sudut-sudut, atau kombinasi keduanya.
- Pahami konsep sisi-sisi-sisi (SSS): Dua segitiga kongruen jika ketiga sisi pada segitiga pertama sama dengan ketiga sisi pada segitiga kedua.
- Pahami konsep sisi-sudut-sisi (SAS): Dua segitiga kongruen jika dua sisi dan sudut yang diapit oleh kedua sisi tersebut pada segitiga pertama sama dengan dua sisi dan sudut yang diapit oleh kedua sisi tersebut pada segitiga kedua.
- Pahami konsep sudut-sisi-sudut (ASA): Dua segitiga kongruen jika dua sudut dan sisi yang diapit oleh kedua sudut tersebut pada segitiga pertama sama dengan dua sudut dan sisi yang diapit oleh kedua sudut tersebut pada segitiga kedua.
- Pahami konsep sudut-sudut-sisi (AAS): Dua segitiga kongruen jika dua sudut dan sisi yang berhadapan dengan salah satu sudut tersebut pada segitiga pertama sama dengan dua sudut dan sisi yang berhadapan dengan salah satu sudut tersebut pada segitiga kedua.
- Perhatikan informasi yang diberikan: Perhatikan informasi yang diberikan dalam soal dan tentukan kriteria kekongruenan yang paling sesuai untuk menyelesaikan soal tersebut.
- Latih dengan contoh soal: Mengerjakan soal-soal latihan adalah cara terbaik untuk memahami konsep kekongruenan segitiga.
Kesimpulan Akhir
Dengan memahami contoh soal kesebangunan dan kekongruenan segitiga, Anda akan memiliki pemahaman yang lebih mendalam tentang konsep-konsep geometri yang penting. Penerapan konsep ini tidak hanya terbatas pada bidang matematika, tetapi juga memiliki peran penting dalam berbagai bidang kehidupan. Semoga contoh soal yang disajikan dapat membantu Anda dalam menguasai konsep ini dan membuka cakrawala pemahaman Anda tentang geometri.






