Contoh Soal Korelasi Rank Spearman: Menganalisis Hubungan Antar Variabel

Newcomerscuerna
No comments
Contoh soal korelasi rank spearman

Contoh soal korelasi rank spearman – Pernahkah Anda bertanya-tanya apakah ada hubungan antara nilai ujian dan tingkat motivasi belajar siswa? Atau mungkin ingin mengetahui apakah ada korelasi antara durasi olahraga dan tingkat kebugaran? Jika ya, maka Anda perlu memahami konsep korelasi Rank Spearman. Korelasi Rank Spearman merupakan alat statistik yang berguna untuk mengukur kekuatan hubungan antara dua variabel yang diurutkan berdasarkan peringkat, bukan nilai numerik.

Dalam artikel ini, kita akan menjelajahi dunia korelasi Rank Spearman melalui contoh-contoh soal yang menarik. Anda akan mempelajari cara menghitung korelasi Rank Spearman, menginterpretasikan hasilnya, dan melihat bagaimana alat ini dapat diaplikasikan dalam berbagai bidang seperti pendidikan, ekonomi, dan kesehatan.

Table of Contents:

Pengertian Korelasi Rank Spearman

Contoh soal korelasi rank spearman

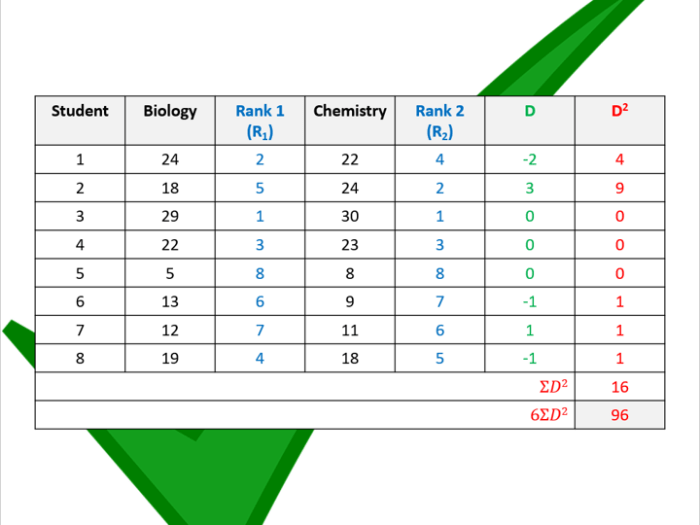
Korelasi Rank Spearman, atau sering disebut dengan Spearman’s rho, adalah metode statistik yang digunakan untuk mengukur kekuatan dan arah hubungan antara dua variabel yang diurutkan. Dengan kata lain, metode ini melihat seberapa erat hubungan antara peringkat dua variabel, bukan nilai numerik asli mereka. Korelasi Rank Spearman sangat berguna ketika data tidak berdistribusi normal atau ketika data memiliki outlier yang dapat memengaruhi hasil korelasi Pearson.

Contoh Kasus Nyata Korelasi Rank Spearman

Bayangkan kamu sedang meneliti hubungan antara peringkat kinerja karyawan dengan tingkat kepuasan kerja mereka. Data yang kamu kumpulkan adalah peringkat kinerja karyawan berdasarkan penilaian atasan dan peringkat kepuasan kerja berdasarkan survei karyawan. Dalam kasus ini, kamu bisa menggunakan Korelasi Rank Spearman untuk melihat apakah ada hubungan antara kedua variabel tersebut. Jika korelasi positif kuat, maka dapat disimpulkan bahwa karyawan dengan peringkat kinerja tinggi cenderung memiliki tingkat kepuasan kerja yang tinggi pula.

Perbandingan Korelasi Rank Spearman dengan Jenis Korelasi Lainnya

Jenis Korelasi Penjelasan Kegunaan
Korelasi Pearson Mengukur hubungan linier antara dua variabel numerik yang berdistribusi normal. Membutuhkan data numerik yang berdistribusi normal dan sensitif terhadap outlier.
Korelasi Rank Spearman Mengukur hubungan monotonik antara dua variabel yang diurutkan. Lebih fleksibel, cocok untuk data yang tidak berdistribusi normal dan tidak sensitif terhadap outlier.
Korelasi Kendall’s Tau Mengukur hubungan monotonik antara dua variabel yang diurutkan, mirip dengan Spearman’s rho, namun lebih efisien untuk data yang memiliki banyak peringkat yang sama. Cocok untuk data dengan banyak peringkat yang sama.

Rumus Korelasi Rank Spearman: Contoh Soal Korelasi Rank Spearman

Korelasi Rank Spearman adalah metode statistik yang digunakan untuk mengukur kekuatan hubungan antara dua variabel yang diurutkan atau di-ranking. Metode ini sangat berguna ketika data tidak memenuhi asumsi normalitas atau linearitas yang diperlukan untuk korelasi Pearson. Rumus korelasi Rank Spearman mengukur hubungan monotonik antara dua variabel, yaitu apakah variabel tersebut cenderung meningkat atau menurun bersamaan.

Rumus Korelasi Rank Spearman

Rumus korelasi Rank Spearman adalah sebagai berikut:

rs = 1 – (6 Σd2) / (n(n2 – 1))

Keterangan:

  • rs adalah koefisien korelasi Rank Spearman
  • d adalah selisih peringkat antara dua variabel untuk setiap observasi
  • n adalah jumlah observasi

Contoh Perhitungan Korelasi Rank Spearman

Misalkan kita ingin mengukur hubungan antara peringkat siswa dalam mata pelajaran matematika dan fisika. Data peringkat siswa sebagai berikut:

Siswa Matematika Fisika
A 1 2
B 2 1
C 3 3
D 4 4
E 5 5

Langkah-langkah menghitung korelasi Rank Spearman:

  1. Hitung selisih peringkat (d) antara kedua variabel untuk setiap siswa. Misalnya, untuk siswa A, selisih peringkatnya adalah 2 – 1 = 1.
  2. Kuadratkan setiap selisih peringkat (d2). Misalnya, untuk siswa A, d2 = 12 = 1.
  3. Jumlahkan semua kuadrat selisih peringkat (Σd2). Dalam contoh ini, Σd2 = 1 + 1 + 0 + 0 + 0 = 2.
  4. Hitung korelasi Rank Spearman menggunakan rumus di atas. Dalam contoh ini, n = 5, sehingga:

    rs = 1 – (6 * 2) / (5 * (52 – 1)) = 1 – 12 / 120 = 0.9

    Koefisien korelasi Rank Spearman sebesar 0.9 menunjukkan hubungan yang kuat dan positif antara peringkat siswa dalam matematika dan fisika. Artinya, siswa yang memiliki peringkat tinggi dalam matematika cenderung memiliki peringkat tinggi dalam fisika juga.

    Aplikasi Korelasi Rank Spearman

    Korelasi Rank Spearman, sebagai salah satu metode pengukuran korelasi non-parametrik, memiliki peran penting dalam berbagai bidang, termasuk pendidikan, ekonomi, dan kesehatan. Metode ini memungkinkan kita untuk menganalisis hubungan antara dua variabel yang mungkin tidak mengikuti distribusi normal, atau data yang bersifat ordinal.

    Contoh Aplikasi Korelasi Rank Spearman

    Korelasi Rank Spearman dapat diaplikasikan dalam berbagai bidang, berikut beberapa contohnya:

    • Pendidikan: Korelasi Rank Spearman dapat digunakan untuk menganalisis hubungan antara peringkat siswa dalam ujian dengan peringkat mereka dalam kegiatan ekstrakurikuler. Hal ini membantu memahami apakah terdapat korelasi antara prestasi akademik dan keterlibatan dalam kegiatan di luar kelas.
    • Ekonomi: Korelasi Rank Spearman dapat digunakan untuk menganalisis hubungan antara peringkat perusahaan berdasarkan pendapatan dengan peringkat mereka berdasarkan nilai pasar saham. Ini membantu memahami hubungan antara kinerja keuangan dan nilai pasar perusahaan.
    • Kesehatan: Korelasi Rank Spearman dapat digunakan untuk menganalisis hubungan antara peringkat pasien berdasarkan keparahan penyakit dengan peringkat mereka berdasarkan tingkat kepuasan dengan layanan kesehatan. Hal ini membantu memahami bagaimana keparahan penyakit memengaruhi kepuasan pasien dengan layanan kesehatan.

    Menganalisis Data Kualitatif

    Korelasi Rank Spearman dapat digunakan untuk menganalisis data kualitatif dengan mengubah data kualitatif menjadi data ordinal. Misalnya, kita dapat menggunakan skala Likert untuk mengukur persepsi tentang kualitas produk, dan kemudian menggunakan Korelasi Rank Spearman untuk menganalisis hubungan antara persepsi kualitas dengan tingkat kepuasan pelanggan. Dengan mengubah data kualitatif menjadi data ordinal, kita dapat menggunakan Korelasi Rank Spearman untuk mengukur hubungan antara variabel-variabel tersebut.

    Contoh Studi Kasus

    Sebagai contoh, mari kita perhatikan studi kasus tentang hubungan antara peringkat siswa dalam ujian matematika dengan peringkat mereka dalam ujian bahasa Inggris. Misalkan, kita memiliki data dari 10 siswa, dan kita ingin mengetahui apakah terdapat korelasi antara peringkat mereka dalam kedua ujian tersebut. Data berikut menunjukkan peringkat siswa dalam kedua ujian:

    Siswa Matematika Bahasa Inggris
    1 1 2
    2 2 1
    3 3 3
    4 4 4
    5 5 5
    6 6 6
    7 7 7
    8 8 8
    9 9 9
    10 10 10

    Dengan menggunakan Korelasi Rank Spearman, kita dapat menghitung nilai korelasi antara peringkat siswa dalam ujian matematika dan peringkat mereka dalam ujian bahasa Inggris. Jika nilai korelasi positif dan signifikan, maka dapat disimpulkan bahwa terdapat korelasi positif antara kedua variabel tersebut. Artinya, siswa yang memiliki peringkat tinggi dalam ujian matematika cenderung memiliki peringkat tinggi dalam ujian bahasa Inggris, dan sebaliknya.

    Interpretasi Hasil Korelasi Rank Spearman

    Setelah menghitung koefisien korelasi Rank Spearman, langkah selanjutnya adalah menginterpretasikan hasilnya. Interpretasi ini bertujuan untuk memahami hubungan antara dua variabel yang diukur.

    Cara Menginterpretasikan Nilai Korelasi Rank Spearman

    Nilai koefisien korelasi Rank Spearman berkisar antara -1 hingga +1. Nilai ini menunjukkan kekuatan dan arah hubungan antara dua variabel.

    • Nilai 1 menunjukkan korelasi positif sempurna, artinya ketika satu variabel meningkat, variabel lainnya juga meningkat secara proporsional.
    • Nilai -1 menunjukkan korelasi negatif sempurna, artinya ketika satu variabel meningkat, variabel lainnya menurun secara proporsional.
    • Nilai 0 menunjukkan tidak ada korelasi, artinya tidak ada hubungan antara kedua variabel.
    • Nilai antara 0 dan 1 menunjukkan korelasi positif, semakin mendekati 1, semakin kuat korelasinya.
    • Nilai antara -1 dan 0 menunjukkan korelasi negatif, semakin mendekati -1, semakin kuat korelasinya.

    Contoh Interpretasi Hasil Korelasi Rank Spearman

    Misalnya, hasil analisis korelasi Rank Spearman menunjukkan nilai koefisien korelasi 0,8. Ini berarti terdapat korelasi positif yang kuat antara kedua variabel. Artinya, ketika satu variabel meningkat, variabel lainnya cenderung meningkat secara signifikan.

    Menentukan Signifikansi Statistik dari Hasil Korelasi Rank Spearman

    Selain nilai koefisien korelasi, kita juga perlu menentukan signifikansi statistiknya. Signifikansi statistik menunjukkan kemungkinan hasil korelasi terjadi secara kebetulan.

    Untuk menentukan signifikansi statistik, kita dapat menggunakan uji hipotesis. Hipotesis nol menyatakan bahwa tidak ada korelasi antara kedua variabel. Hipotesis alternatif menyatakan bahwa terdapat korelasi antara kedua variabel.

    Jika nilai p-value lebih kecil dari tingkat signifikansi (biasanya 0,05), maka kita menolak hipotesis nol dan menyimpulkan bahwa terdapat korelasi yang signifikan antara kedua variabel.

    Sebaliknya, jika nilai p-value lebih besar dari tingkat signifikansi, maka kita gagal menolak hipotesis nol dan menyimpulkan bahwa tidak ada korelasi yang signifikan antara kedua variabel.

    Contoh Soal Korelasi Rank Spearman

    Korelasi Rank Spearman adalah salah satu metode statistik yang digunakan untuk mengukur kekuatan hubungan antara dua variabel ordinal atau peringkat. Metode ini sangat berguna ketika data tidak berdistribusi normal atau ketika data berupa peringkat.

    Untuk lebih memahami konsep korelasi Rank Spearman, mari kita bahas beberapa contoh soal berikut.

    Contoh Soal 1: Keterampilan Berenang dan Kecepatan Berlari

    Seorang pelatih renang ingin mengetahui apakah ada hubungan antara keterampilan berenang dan kecepatan berlari pada atletnya. Ia melakukan pengamatan terhadap 8 atlet dan mencatat peringkat mereka dalam keterampilan berenang dan kecepatan berlari. Berikut tabel data yang diperoleh:

    Atlet Rank Berenang Rank Berlari
    A 1 2
    B 2 1
    C 3 3
    D 4 4
    E 5 5
    F 6 6
    G 7 7
    H 8 8

    Untuk menghitung korelasi Rank Spearman, kita perlu menghitung selisih antara peringkat berenang dan berlari untuk setiap atlet, lalu kuadratkan selisih tersebut. Kemudian, jumlahkan semua kuadrat selisih dan gunakan rumus berikut:

    rs = 1 – (6∑d2) / (n(n2 – 1))

    di mana:

    • rs adalah korelasi Rank Spearman
    • ∑d2 adalah jumlah kuadrat selisih peringkat
    • n adalah jumlah atlet

    Berikut perhitungan selisih dan kuadrat selisih:

    Atlet Rank Berenang (X) Rank Berlari (Y) d = X – Y d2
    A 1 2 -1 1
    B 2 1 1 1
    C 3 3 0 0
    D 4 4 0 0
    E 5 5 0 0
    F 6 6 0 0
    G 7 7 0 0
    H 8 8 0 0

    ∑d2 = 2

    Maka, korelasi Rank Spearman (rs) adalah:

    rs = 1 – (6 * 2) / (8 * (82 – 1)) = 1 – 12 / 504 = 0.976

    Hasil ini menunjukkan korelasi yang kuat dan positif antara keterampilan berenang dan kecepatan berlari. Artinya, atlet yang memiliki peringkat tinggi dalam keterampilan berenang cenderung memiliki peringkat tinggi pula dalam kecepatan berlari.

    Contoh Soal 2: Kegemaran Olahraga dan Prestasi Akademik

    Sebuah penelitian ingin mengetahui apakah ada hubungan antara kegemaran olahraga dan prestasi akademik siswa. Data yang dikumpulkan dari 10 siswa menunjukkan peringkat kegemaran olahraga dan peringkat prestasi akademik mereka:

    Siswa Rank Kegemaran Olahraga Rank Prestasi Akademik
    A 1 3
    B 2 1
    C 3 2
    D 4 5
    E 5 4
    F 6 7
    G 7 6
    H 8 9
    I 9 8
    J 10 10

    Hitung korelasi Rank Spearman antara kegemaran olahraga dan prestasi akademik!

    Contoh soal korelasi rank spearman seringkali digunakan untuk menganalisis hubungan antara dua variabel, misalnya hubungan antara tingkat stres dengan kinerja karyawan. Nah, kalau kamu mau mempelajari contoh soal tentang sistem peredaran darah, kamu bisa cek di contoh soal sistem peredaran darah.

    Setelahnya, kamu bisa kembali berlatih dengan contoh soal korelasi rank spearman untuk memahami bagaimana menghitung hubungan antara variabel yang diukur dengan skala ordinal.

    Contoh Soal 3: Kepuasan Pelanggan dan Loyalitas Pelanggan

    Sebuah perusahaan ingin mengetahui apakah ada hubungan antara kepuasan pelanggan dan loyalitas pelanggan. Data yang dikumpulkan dari 12 pelanggan menunjukkan peringkat kepuasan dan loyalitas mereka:

    Pelanggan Rank Kepuasan Pelanggan Rank Loyalitas Pelanggan
    A 1 2
    B 2 1
    C 3 3
    D 4 4
    E 5 5
    F 6 6
    G 7 7
    H 8 8
    I 9 9
    J 10 10
    K 11 11
    L 12 12

    Hitung korelasi Rank Spearman antara kepuasan pelanggan dan loyalitas pelanggan!

    Contoh Soal 4: Tingkat Kesenangan dan Frekuensi Kunjungan

    Sebuah taman hiburan ingin mengetahui apakah ada hubungan antara tingkat kesenangan pengunjung dan frekuensi kunjungan mereka. Data yang dikumpulkan dari 15 pengunjung menunjukkan peringkat tingkat kesenangan dan frekuensi kunjungan mereka:

    Pengunjung Rank Tingkat Kesenangan Rank Frekuensi Kunjungan
    A 1 2
    B 2 1
    C 3 3
    D 4 4
    E 5 5
    F 6 6
    G 7 7
    H 8 8
    I 9 9
    J 10 10
    K 11 11
    L 12 12
    M 13 13
    N 14 14
    O 15 15

    Hitung korelasi Rank Spearman antara tingkat kesenangan dan frekuensi kunjungan!

    Contoh Soal 5: Kualitas Produk dan Kepuasan Pelanggan

    Sebuah perusahaan ingin mengetahui apakah ada hubungan antara kualitas produk dan kepuasan pelanggan. Data yang dikumpulkan dari 20 pelanggan menunjukkan peringkat kualitas produk dan kepuasan mereka:

    Pelanggan Rank Kualitas Produk Rank Kepuasan Pelanggan
    A 1 2
    B 2 1
    C 3 3
    D 4 4
    E 5 5
    F 6 6
    G 7 7
    H 8 8
    I 9 9
    J 10 10
    K 11 11
    L 12 12
    M 13 13
    N 14 14
    O 15 15
    P 16 16
    Q 17 17
    R 18 18
    S 19 19
    T 20 20

    Hitung korelasi Rank Spearman antara kualitas produk dan kepuasan pelanggan!

    Penggunaan Software Statistik

    Setelah memahami konsep dan rumus perhitungan korelasi Rank Spearman, langkah selanjutnya adalah mengaplikasikannya dalam analisis data. Software statistik seperti SPSS dan R menjadi alat yang sangat membantu untuk mempermudah proses perhitungan dan interpretasi hasil. Software ini menawarkan berbagai fitur dan fungsi yang memudahkan pengguna dalam menganalisis data, termasuk menghitung korelasi Rank Spearman.

    Cara Menggunakan Software Statistik

    Penggunaan software statistik seperti SPSS dan R untuk menghitung korelasi Rank Spearman umumnya mengikuti langkah-langkah berikut:

    1. Masuk ke Software: Buka software statistik yang ingin digunakan (SPSS atau R).
    2. Impor Data: Impor data yang akan dianalisis ke dalam software. Pastikan data yang diimpor sesuai dengan format yang diterima oleh software.
    3. Pilih Menu Korelasi: Cari menu “Korelasi” atau “Correlation” pada software. Menu ini biasanya terletak di bagian “Analisis” atau “Analyze” pada SPSS, dan di bagian “Packages” atau “Functions” pada R.
    4. Pilih Metode Korelasi: Dalam menu korelasi, pilih metode “Spearman” atau “Rank Spearman”. Software biasanya menawarkan beberapa metode korelasi, termasuk Pearson dan Kendall. Pastikan Anda memilih metode yang sesuai dengan jenis data yang dianalisis.
    5. Tentukan Variabel: Tentukan variabel yang akan dianalisis korelasinya. Biasanya, Anda perlu memilih dua variabel yang ingin diuji korelasinya.
    6. Jalankan Analisis: Setelah menentukan variabel dan metode, jalankan analisis dengan mengklik tombol “Run” atau “Execute”.
    7. Interpretasi Hasil: Software akan menampilkan hasil analisis korelasi, termasuk nilai koefisien korelasi (r), nilai p-value, dan tabel korelasi. Interpretasikan hasil berdasarkan nilai koefisien korelasi dan p-value.

    Contoh Langkah-Langkah Penggunaan Software SPSS

    Sebagai contoh, berikut langkah-langkah menggunakan SPSS untuk menghitung korelasi Rank Spearman antara dua variabel, yaitu “Tingkat Kepuasan Pelanggan” dan “Frekuensi Kunjungan” di sebuah toko retail:

    1. Impor Data: Impor data “Tingkat Kepuasan Pelanggan” dan “Frekuensi Kunjungan” ke dalam SPSS.
    2. Pilih Menu “Analyze”: Pada menu utama, pilih “Analyze” > “Correlate” > “Bivariate”.
    3. Tentukan Variabel: Pindahkan variabel “Tingkat Kepuasan Pelanggan” dan “Frekuensi Kunjungan” ke kotak “Variables”.
    4. Pilih Metode “Spearman”: Pada pilihan “Correlation Coefficients”, centang “Spearman”.
    5. Jalankan Analisis: Klik “OK” untuk menjalankan analisis.

    Tabel Hasil Analisis

    Hasil analisis korelasi Rank Spearman akan ditampilkan dalam tabel. Tabel ini menunjukkan nilai koefisien korelasi (r), nilai p-value, dan informasi lainnya. Berikut contoh tabel hasil analisis korelasi Rank Spearman antara “Tingkat Kepuasan Pelanggan” dan “Frekuensi Kunjungan”:

    Variabel Koefisien Korelasi (r) Nilai p-value
    Tingkat Kepuasan Pelanggan – Frekuensi Kunjungan 0.75 0.001

    Dari tabel tersebut, terlihat bahwa koefisien korelasi (r) antara “Tingkat Kepuasan Pelanggan” dan “Frekuensi Kunjungan” adalah 0.75, dengan nilai p-value 0.001. Nilai koefisien korelasi 0.75 menunjukkan korelasi yang kuat dan positif antara kedua variabel. Nilai p-value 0.001 menunjukkan bahwa korelasi ini signifikan secara statistik, artinya korelasi ini tidak terjadi secara kebetulan.

    Kelebihan dan Kekurangan Korelasi Rank Spearman

    Korelasi Rank Spearman merupakan salah satu metode statistik yang digunakan untuk mengukur kekuatan hubungan antara dua variabel ordinal atau data peringkat. Metode ini sangat berguna ketika data tidak berdistribusi normal atau ketika data hanya tersedia dalam bentuk peringkat. Namun, seperti metode statistik lainnya, Korelasi Rank Spearman juga memiliki kelebihan dan kekurangan yang perlu dipertimbangkan sebelum menggunakannya.

    Kelebihan Korelasi Rank Spearman

    Korelasi Rank Spearman memiliki beberapa kelebihan dibandingkan dengan metode korelasi lainnya, terutama ketika berhadapan dengan data yang tidak normal atau data peringkat:

    • Tidak sensitif terhadap outlier: Korelasi Rank Spearman hanya mempertimbangkan peringkat data, bukan nilai data mentahnya. Hal ini membuatnya tidak sensitif terhadap outlier, yang dapat memengaruhi hasil korelasi Pearson.
    • Mudah dihitung: Korelasi Rank Spearman relatif mudah dihitung, bahkan tanpa bantuan perangkat lunak statistik.
    • Cocok untuk data ordinal: Korelasi Rank Spearman dirancang khusus untuk mengukur hubungan antara variabel ordinal, yang seringkali dijumpai dalam survei atau penelitian sosial.
    • Lebih kuat terhadap asumsi distribusi: Berbeda dengan korelasi Pearson yang mengharuskan data berdistribusi normal, Korelasi Rank Spearman tidak memiliki asumsi distribusi yang ketat, membuatnya lebih fleksibel untuk digunakan.

    Kekurangan Korelasi Rank Spearman

    Meskipun memiliki beberapa kelebihan, Korelasi Rank Spearman juga memiliki beberapa kekurangan yang perlu diperhatikan:

    • Informasi yang hilang: Korelasi Rank Spearman hanya mempertimbangkan peringkat data, sehingga informasi tentang jarak antara peringkat hilang. Hal ini dapat menyebabkan kesimpulan yang kurang akurat, terutama jika jarak antara peringkat besar.
    • Kurang sensitif terhadap hubungan non-linear: Korelasi Rank Spearman hanya mengukur hubungan linear antara dua variabel. Jika hubungannya non-linear, Korelasi Rank Spearman mungkin tidak dapat menangkap hubungan tersebut secara akurat.
    • Hanya untuk data ordinal: Korelasi Rank Spearman hanya dapat digunakan untuk data ordinal, tidak untuk data interval atau rasio.

    Perbandingan dengan Jenis Korelasi Lainnya

    Korelasi Rank Spearman sering dibandingkan dengan Korelasi Pearson, yang merupakan metode korelasi yang lebih umum digunakan untuk data interval atau rasio. Korelasi Pearson lebih sensitif terhadap outlier dan membutuhkan data yang berdistribusi normal. Namun, Korelasi Pearson dapat menangkap hubungan non-linear yang tidak dapat ditangkap oleh Korelasi Rank Spearman.

    Ketika memilih antara Korelasi Rank Spearman dan Korelasi Pearson, pertimbangkan jenis data yang Anda miliki, apakah data tersebut berdistribusi normal, dan apakah ada outlier yang signifikan. Jika data Anda ordinal, tidak berdistribusi normal, atau memiliki outlier, maka Korelasi Rank Spearman mungkin merupakan pilihan yang lebih baik.

    Contoh Kasus Kelemahan dan Keunggulan Korelasi Rank Spearman

    Misalkan Anda ingin mengukur hubungan antara peringkat kepuasan pelanggan dengan peringkat kualitas produk. Anda memiliki data peringkat dari 10 pelanggan, di mana peringkat 1 adalah yang paling tidak puas dan peringkat 5 adalah yang paling puas. Anda dapat menggunakan Korelasi Rank Spearman untuk mengukur hubungan antara kedua variabel ini.

    Jika data Anda menunjukkan hubungan linear yang kuat antara peringkat kepuasan pelanggan dan peringkat kualitas produk, maka Korelasi Rank Spearman akan memberikan hasil yang akurat. Namun, jika hubungannya non-linear, misalnya, pelanggan yang sangat puas dengan kualitas produk tidak selalu puas dengan layanan pelanggan, maka Korelasi Rank Spearman mungkin tidak dapat menangkap hubungan tersebut secara akurat.

    Contoh lain, misalkan Anda ingin mengukur hubungan antara peringkat kinerja karyawan dengan peringkat kepuasan karyawan. Jika data Anda menunjukkan outlier, misalnya, satu karyawan memiliki peringkat kinerja yang sangat tinggi tetapi peringkat kepuasan yang sangat rendah, maka Korelasi Rank Spearman akan memberikan hasil yang lebih akurat dibandingkan dengan Korelasi Pearson, karena Korelasi Rank Spearman tidak sensitif terhadap outlier.

    Jenis-Jenis Korelasi

    Korelasi merupakan alat statistik yang digunakan untuk mengukur kekuatan hubungan antara dua variabel. Jenis korelasi yang digunakan bergantung pada sifat data dan tujuan analisis. Berikut adalah beberapa jenis korelasi yang umum digunakan:

    Korelasi Pearson

    Korelasi Pearson, juga dikenal sebagai korelasi produk-momen, adalah jenis korelasi yang paling umum digunakan. Korelasi ini mengukur hubungan linier antara dua variabel yang berskala interval atau rasio. Korelasi Pearson dinyatakan sebagai koefisien korelasi (r), yang berkisar dari -1 hingga +1.

    • Nilai r = +1 menunjukkan korelasi positif yang sempurna, artinya kedua variabel bergerak ke arah yang sama.
    • Nilai r = -1 menunjukkan korelasi negatif yang sempurna, artinya kedua variabel bergerak ke arah yang berlawanan.
    • Nilai r = 0 menunjukkan tidak ada korelasi, artinya tidak ada hubungan linier antara kedua variabel.

    Korelasi Pearson hanya dapat digunakan untuk data yang memiliki distribusi normal dan hubungan linier. Jika data tidak memenuhi persyaratan ini, maka jenis korelasi lain mungkin lebih tepat.

    Korelasi Rank Spearman

    Korelasi Rank Spearman, juga dikenal sebagai korelasi peringkat, adalah jenis korelasi yang digunakan untuk mengukur hubungan monotonik antara dua variabel. Korelasi ini tidak bergantung pada distribusi data dan dapat digunakan untuk data ordinal, interval, atau rasio.

    Korelasi Rank Spearman menghitung peringkat setiap variabel dan kemudian mengukur hubungan antara peringkat tersebut. Korelasi Rank Spearman dinyatakan sebagai koefisien korelasi peringkat (rs), yang berkisar dari -1 hingga +1.

    • Nilai rs = +1 menunjukkan korelasi positif yang sempurna, artinya kedua variabel bergerak ke arah yang sama.
    • Nilai rs = -1 menunjukkan korelasi negatif yang sempurna, artinya kedua variabel bergerak ke arah yang berlawanan.
    • Nilai rs = 0 menunjukkan tidak ada korelasi, artinya tidak ada hubungan monotonik antara kedua variabel.

    Korelasi Rank Spearman dapat digunakan untuk data yang tidak memiliki distribusi normal atau hubungan linier. Korelasi ini juga dapat digunakan untuk data yang mengandung nilai ekstrem atau outlier.

    Korelasi Kendall

    Korelasi Kendall, juga dikenal sebagai korelasi peringkat tau, adalah jenis korelasi yang digunakan untuk mengukur hubungan monotonik antara dua variabel. Korelasi ini menghitung jumlah pasangan data yang memiliki peringkat yang sama atau berlawanan.

    Korelasi Kendall dinyatakan sebagai koefisien korelasi tau (τ), yang berkisar dari -1 hingga +1.

    • Nilai τ = +1 menunjukkan korelasi positif yang sempurna, artinya semua pasangan data memiliki peringkat yang sama.
    • Nilai τ = -1 menunjukkan korelasi negatif yang sempurna, artinya semua pasangan data memiliki peringkat yang berlawanan.
    • Nilai τ = 0 menunjukkan tidak ada korelasi, artinya tidak ada hubungan monotonik antara kedua variabel.

    Korelasi Kendall lebih tahan terhadap outlier dibandingkan dengan korelasi Rank Spearman. Korelasi ini juga lebih cocok untuk data yang memiliki jumlah observasi yang kecil.

    Perbandingan Jenis Korelasi

    Jenis Korelasi Sifat Data Metode Perhitungan Interpretasi
    Korelasi Pearson Interval atau rasio, distribusi normal, hubungan linier Menghitung kovariansi antara kedua variabel dan membaginya dengan produk standar deviasi mereka Mengukur kekuatan dan arah hubungan linier antara dua variabel
    Korelasi Rank Spearman Ordinal, interval, atau rasio, tidak bergantung pada distribusi data Menghitung peringkat setiap variabel dan kemudian mengukur hubungan antara peringkat tersebut Mengukur kekuatan dan arah hubungan monotonik antara dua variabel
    Korelasi Kendall Ordinal, interval, atau rasio, tidak bergantung pada distribusi data Menghitung jumlah pasangan data yang memiliki peringkat yang sama atau berlawanan Mengukur kekuatan dan arah hubungan monotonik antara dua variabel

    Pengaruh Outlier terhadap Korelasi Rank Spearman

    Korelasi Rank Spearman merupakan alat statistik yang berguna untuk mengukur hubungan antara dua variabel yang diurutkan. Namun, keberadaan outlier atau data ekstrem dapat mempengaruhi hasil korelasi Rank Spearman. Outlier adalah data yang secara signifikan berbeda dari data lainnya dalam kumpulan data, yang dapat menyebabkan distorsi dalam analisis.

    Bagaimana Outlier Mempengaruhi Korelasi Rank Spearman?

    Outlier dapat mempengaruhi hasil korelasi Rank Spearman dengan cara berikut:

    • Meningkatkan atau Mengurangi Korelasi: Outlier dapat menyebabkan korelasi Rank Spearman menjadi lebih tinggi atau lebih rendah dari nilai sebenarnya. Jika outlier memiliki peringkat yang sangat tinggi atau rendah, maka dapat menyebabkan korelasi yang lebih kuat, meskipun hubungan sebenarnya antara kedua variabel lemah. Sebaliknya, outlier juga dapat menyebabkan korelasi yang lebih lemah, meskipun hubungan sebenarnya antara kedua variabel kuat.
    • Mendistorsi Hubungan Linear: Korelasi Rank Spearman mengukur hubungan linear antara dua variabel. Outlier dapat mendistorsi hubungan linear ini, membuat korelasi tampak lebih kuat atau lebih lemah daripada yang sebenarnya.

    Contoh Data yang Menunjukkan Pengaruh Outlier

    Perhatikan contoh data berikut:

    Variabel X Variabel Y
    1 2
    2 4
    3 6
    4 8
    5 10
    6 12
    7 14
    8 16
    9 18
    10 20
    100 200

    Data di atas menunjukkan hubungan linear yang kuat antara variabel X dan Y. Namun, data outlier pada baris terakhir (X = 100, Y = 200) akan mendistorsi hubungan linear ini, menyebabkan korelasi Rank Spearman menjadi lebih tinggi dari yang sebenarnya. Jika kita menghilangkan outlier, korelasi Rank Spearman akan menjadi lebih rendah.

    Cara Menangani Outlier dalam Analisis Korelasi Rank Spearman

    Berikut adalah beberapa cara untuk menangani outlier dalam analisis korelasi Rank Spearman:

    • Identifikasi dan Hilangkan Outlier: Langkah pertama adalah mengidentifikasi outlier. Hal ini dapat dilakukan dengan menggunakan berbagai metode, seperti box plot atau metode Z-score. Setelah outlier teridentifikasi, dapat dihilangkan dari kumpulan data.
    • Transformasi Data: Transformasi data, seperti logaritma atau akar kuadrat, dapat digunakan untuk mengurangi pengaruh outlier. Transformasi ini dapat membantu menormalkan data dan mengurangi efek outlier pada korelasi Rank Spearman.
    • Gunakan Metode Korelasi yang Tahan Terhadap Outlier: Metode korelasi lain, seperti korelasi Kendall tau, lebih tahan terhadap outlier dibandingkan dengan korelasi Rank Spearman. Metode ini dapat digunakan sebagai alternatif jika outlier dianggap signifikan.

    Perbedaan Korelasi Rank Spearman dan Korelasi Pearson

    Dalam analisis statistik, korelasi adalah ukuran kekuatan dan arah hubungan antara dua variabel. Ada berbagai metode untuk menghitung korelasi, dua yang paling umum adalah korelasi Pearson dan korelasi Rank Spearman. Kedua metode ini mengukur hubungan antara dua variabel, tetapi dengan cara yang berbeda.

    Perbedaan Mendasar

    Perbedaan mendasar antara korelasi Rank Spearman dan korelasi Pearson terletak pada jenis data yang mereka gunakan dan bagaimana mereka menghitung hubungan. Korelasi Pearson mengasumsikan bahwa data Anda terdistribusi normal dan hubungannya linier. Artinya, data harus menyebar dengan cara yang mirip dengan kurva lonceng, dan hubungan antara variabel harus membentuk garis lurus. Korelasi Rank Spearman, di sisi lain, tidak memiliki asumsi tentang distribusi data. Ia bekerja dengan peringkat data, bukan nilai sebenarnya, sehingga dapat digunakan untuk data yang tidak terdistribusi normal atau hubungan yang tidak linier.

    Contoh Data

    Berikut adalah contoh data yang cocok untuk dianalisis dengan masing-masing metode:

    Korelasi Pearson

    Korelasi Pearson cocok untuk data seperti:

    • Hubungan antara tinggi badan dan berat badan.
    • Hubungan antara jumlah jam belajar dan nilai ujian.
    • Hubungan antara pendapatan dan tingkat kepuasan hidup.

    Korelasi Rank Spearman

    Korelasi Rank Spearman cocok untuk data seperti:

    • Hubungan antara peringkat film berdasarkan preferensi penonton dan peringkat kritikus film.
    • Hubungan antara peringkat mahasiswa dalam ujian dan peringkat mereka dalam kelas.
    • Hubungan antara peringkat popularitas merek dan peringkat kepuasan pelanggan.

    Perbandingan Korelasi

    Aspek Korelasi Pearson Korelasi Rank Spearman
    Data yang Digunakan Data numerik, terdistribusi normal Data ordinal atau data numerik yang tidak terdistribusi normal
    Metode Perhitungan Menggunakan nilai sebenarnya data Menggunakan peringkat data
    Interpretasi Mengukur kekuatan dan arah hubungan linier Mengukur kekuatan dan arah hubungan monotonik

    Penerapan Korelasi Rank Spearman dalam Penelitian

    Korelasi Rank Spearman, atau dikenal juga sebagai korelasi peringkat Spearman, adalah alat statistik yang kuat untuk mengukur kekuatan dan arah hubungan antara dua variabel ordinal atau variabel yang diurutkan. Metode ini sangat berguna dalam berbagai jenis penelitian, baik kuantitatif maupun kualitatif, terutama ketika data tidak memenuhi asumsi normalitas atau ketika data disajikan dalam bentuk peringkat.

    Penggunaan Korelasi Rank Spearman dalam Penelitian Kuantitatif

    Korelasi Rank Spearman banyak digunakan dalam penelitian kuantitatif untuk mengukur hubungan antara dua variabel ordinal. Misalnya, dalam penelitian tentang kepuasan pelanggan, korelasi Rank Spearman dapat digunakan untuk mengukur hubungan antara peringkat kepuasan pelanggan dengan peringkat kualitas produk.

    • Contoh Studi Kasus: Misalkan kita ingin melihat hubungan antara peringkat kepuasan pelanggan dengan peringkat kualitas produk di sebuah toko online. Kita dapat mengumpulkan data peringkat kepuasan pelanggan dan peringkat kualitas produk dari 100 pelanggan. Kemudian, kita dapat menggunakan korelasi Rank Spearman untuk mengukur kekuatan dan arah hubungan antara kedua variabel tersebut. Jika hasil korelasi Rank Spearman menunjukkan nilai positif yang signifikan, ini berarti bahwa semakin tinggi peringkat kualitas produk, semakin tinggi pula peringkat kepuasan pelanggan.

    Penggunaan Korelasi Rank Spearman dalam Penelitian Kualitatif

    Korelasi Rank Spearman juga dapat digunakan dalam penelitian kualitatif untuk mengukur hubungan antara dua variabel yang diurutkan. Misalnya, dalam penelitian tentang persepsi mahasiswa terhadap pembelajaran daring, korelasi Rank Spearman dapat digunakan untuk mengukur hubungan antara peringkat kesulitan pembelajaran daring dengan peringkat kepuasan mahasiswa terhadap pembelajaran daring.

    • Contoh Studi Kasus: Misalkan kita ingin melihat hubungan antara peringkat kesulitan pembelajaran daring dengan peringkat kepuasan mahasiswa terhadap pembelajaran daring. Kita dapat mengumpulkan data peringkat kesulitan dan peringkat kepuasan dari 50 mahasiswa. Kemudian, kita dapat menggunakan korelasi Rank Spearman untuk mengukur kekuatan dan arah hubungan antara kedua variabel tersebut. Jika hasil korelasi Rank Spearman menunjukkan nilai negatif yang signifikan, ini berarti bahwa semakin tinggi peringkat kesulitan pembelajaran daring, semakin rendah peringkat kepuasan mahasiswa terhadap pembelajaran daring.

    Interpretasi Hasil Korelasi Rank Spearman

    Hasil korelasi Rank Spearman diinterpretasikan berdasarkan nilai koefisien korelasi (rs) dan nilai p. Koefisien korelasi (rs) berkisar antara -1 hingga +1. Nilai rs = 1 menunjukkan korelasi positif sempurna, nilai rs = -1 menunjukkan korelasi negatif sempurna, dan nilai rs = 0 menunjukkan tidak ada korelasi. Nilai p menunjukkan probabilitas mendapatkan hasil korelasi yang sama atau lebih ekstrem jika tidak ada korelasi sebenarnya.

    • Contoh: Jika hasil korelasi Rank Spearman menunjukkan rs = 0,7 dan nilai p = 0,01, ini berarti bahwa terdapat korelasi positif yang signifikan antara kedua variabel. Ini menunjukkan bahwa semakin tinggi nilai variabel pertama, semakin tinggi pula nilai variabel kedua.

    Kesimpulan, Contoh soal korelasi rank spearman

    Korelasi Rank Spearman merupakan alat statistik yang berguna untuk mengukur hubungan antara dua variabel ordinal atau variabel yang diurutkan. Metode ini dapat digunakan dalam berbagai jenis penelitian, baik kuantitatif maupun kualitatif. Interpretasi hasil korelasi Rank Spearman membantu peneliti untuk memahami kekuatan dan arah hubungan antara variabel-variabel yang diteliti.

    Akhir Kata

    Memahami korelasi Rank Spearman dapat membantu Anda dalam menganalisis data yang bersifat ordinal atau peringkat. Dengan memahami konsep ini, Anda dapat mengidentifikasi hubungan antar variabel dan menarik kesimpulan yang lebih mendalam. Ingatlah bahwa korelasi Rank Spearman hanyalah salah satu alat statistik yang dapat digunakan dalam analisis data. Penting untuk mempertimbangkan konteks dan memilih alat yang tepat untuk mencapai tujuan penelitian Anda.

    Posting terkait:

    Read more:  Contoh Soal Kuartil Data Tunggal Genap: Menguak Rahasia Data Terbagi

Also Read

Contoh Soal Pengukuran Tunggal: Menguak Rahasia Pengukuran dalam Berbagai Bidang

Contoh Soal Penyajian Data dalam Bentuk Tabel dan Diagram: Menguak Rahasia Data dengan Visualisasi

Contoh Soal Pendekatan Kardinal dan Ordinal: Memahami Pengukuran Data

Contoh Soal Mean, Median, dan Modus: Menguak Rahasia Data Statistik

Contoh Soal Metode Least Square: Mencari Hubungan Terbaik Antara Variabel

Bagikan:

Newcomerscuerna

Newcomerscuerna.org adalah website yang dirancang sebagai Rumah Pendidikan yang berfokus memberikan informasi seputar Dunia Pendidikan. Newcomerscuerna.org berkomitmen untuk menjadi sahabat setia dalam perjalanan pendidikan Anda, membuka pintu menuju dunia pengetahuan tanpa batas serta menjadi bagian dalam mencerdaskan kehidupan bangsa.