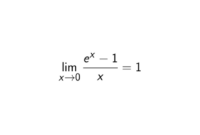Contoh soal limit tak hingga fungsi aljabar – Limit tak hingga fungsi aljabar adalah konsep yang menarik dalam matematika. Bayangkan sebuah fungsi yang terus-menerus naik atau turun tanpa batas. Limit tak hingga membantu kita memahami bagaimana fungsi tersebut berperilaku saat variabelnya menuju nilai tak terhingga. Konsep ini memiliki aplikasi yang luas, mulai dari menghitung kecepatan objek yang bergerak sangat cepat hingga memahami perilaku pasar saham.
Dalam artikel ini, kita akan menjelajahi konsep limit tak hingga fungsi aljabar dengan lebih detail. Kita akan membahas definisi, sifat-sifat, metode penghitungan, dan contoh-contoh soal yang akan membantu Anda memahami topik ini secara lebih mendalam.
Pengertian Limit Tak Hingga Fungsi Aljabar
Limit tak hingga fungsi aljabar adalah konsep yang mengkaji perilaku fungsi saat variabel bebasnya mendekati nilai tak hingga. Dalam konteks ini, tak hingga diartikan sebagai nilai yang sangat besar, baik positif maupun negatif. Limit tak hingga fungsi aljabar membantu kita memahami bagaimana fungsi tersebut berperilaku dalam jangka panjang.
Contoh Fungsi Aljabar yang Memiliki Limit Tak Hingga
Contoh fungsi aljabar yang memiliki limit tak hingga adalah fungsi rasional, yaitu fungsi yang berbentuk pecahan dengan variabel bebas di pembilang dan penyebut. Misalnya, fungsi f(x) = (x^2 + 1) / (x – 1) memiliki limit tak hingga saat x mendekati 1. Hal ini karena saat x mendekati 1, penyebutnya mendekati 0, sementara pembilangnya mendekati 2. Oleh karena itu, nilai fungsi akan semakin besar dan mendekati tak hingga.
Perbedaan Limit Tak Hingga Fungsi Aljabar dan Limit Biasa, Contoh soal limit tak hingga fungsi aljabar
Perbedaan utama antara limit tak hingga fungsi aljabar dan limit biasa terletak pada nilai yang didekati oleh variabel bebas. Pada limit biasa, variabel bebas mendekati suatu nilai tertentu, sementara pada limit tak hingga, variabel bebas mendekati tak hingga. Berikut tabel yang menunjukkan perbedaan keduanya:
| Aspek | Limit Biasa | Limit Tak Hingga |
|---|---|---|
| Nilai yang didekati oleh variabel bebas | Nilai tertentu | Tak hingga |
| Tujuan analisis | Mencari nilai fungsi saat variabel bebas mendekati nilai tertentu | Mencari perilaku fungsi saat variabel bebas mendekati tak hingga |
| Contoh | Limit x mendekati 2 dari fungsi f(x) = x^2 + 1 | Limit x mendekati tak hingga dari fungsi f(x) = (x^2 + 1) / (x – 1) |
Sifat-Sifat Limit Tak Hingga Fungsi Aljabar
Limit tak hingga pada fungsi aljabar adalah konsep yang menarik. Ini membantu kita memahami bagaimana fungsi berperilaku saat variabel inputnya mendekati nilai yang sangat besar atau sangat kecil. Dalam memahami konsep ini, terdapat beberapa sifat yang perlu kita pahami agar kita dapat dengan mudah menyelesaikan soal limit tak hingga fungsi aljabar.
Sifat-Sifat Limit Tak Hingga Fungsi Aljabar
Berikut adalah beberapa sifat limit tak hingga fungsi aljabar yang perlu Anda ketahui:
-
Sifat 1: Limit Fungsi Konstan
Limit dari fungsi konstan c saat x mendekati tak hingga sama dengan konstanta itu sendiri.
limx→∞ c = c
Contoh: limx→∞ 5 = 5
-
Sifat 2: Limit Fungsi Linear
Limit dari fungsi linear ax + b saat x mendekati tak hingga sama dengan tak hingga jika a positif, dan sama dengan negatif tak hingga jika a negatif.
limx→∞ (ax + b) = ∞ jika a > 0
limx→∞ (ax + b) = -∞ jika a < 0
Contoh: limx→∞ (2x + 3) = ∞ dan limx→∞ (-3x + 1) = -∞
-
Sifat 3: Limit Fungsi Polinomial
Limit dari fungsi polinomial anxn + an-1xn-1 + … + a1x + a0 saat x mendekati tak hingga sama dengan tak hingga jika koefisien suku dengan pangkat tertinggi (an) positif, dan sama dengan negatif tak hingga jika an negatif.
limx→∞ (anxn + an-1xn-1 + … + a1x + a0) = ∞ jika an > 0
limx→∞ (anxn + an-1xn-1 + … + a1x + a0) = -∞ jika an < 0
Contoh: limx→∞ (x3 – 2x2 + 5) = ∞ dan limx→∞ (-2x4 + 3x2 – 1) = -∞
-
Sifat 4: Limit Fungsi Rasional
Limit dari fungsi rasional f(x) / g(x) saat x mendekati tak hingga dapat ditentukan dengan membagi pembilang dan penyebut dengan xn, di mana n adalah pangkat tertinggi dari x di pembilang atau penyebut.
limx→∞ [f(x) / g(x)] = limx→∞ [(anxn + an-1xn-1 + … + a1x + a0) / (bmxm + bm-1xm-1 + … + b1x + b0)]
= limx→∞ [(an + an-1/x + … + a1/xn-1 + a0/xn) / (bm + bm-1/x + … + b1/xm-1 + b0/xm)]
Jika n > m, maka limitnya sama dengan tak hingga atau negatif tak hingga, tergantung pada tanda an dan bm. Jika n = m, maka limitnya sama dengan an / bm. Jika n < m, maka limitnya sama dengan 0.
Contoh: limx→∞ [(2x2 + 3x – 1) / (x3 – 2x + 5)] = limx→∞ [(2 + 3/x – 1/x2) / (1 – 2/x2 + 5/x3)] = 0
Contoh Penerapan Sifat Limit Tak Hingga
Misalnya, kita ingin mencari limit dari fungsi f(x) = (3x2 + 2x – 1) / (x2 – 4) saat x mendekati tak hingga.
Berdasarkan sifat limit fungsi rasional, kita dapat membagi pembilang dan penyebut dengan x2:
limx→∞ [(3x2 + 2x – 1) / (x2 – 4)] = limx→∞ [(3 + 2/x – 1/x2) / (1 – 4/x2)]
Ketika x mendekati tak hingga, suku-suku yang mengandung 1/x dan 1/x2 akan mendekati 0. Sehingga:
limx→∞ [(3 + 2/x – 1/x2) / (1 – 4/x2)] = (3 + 0 – 0) / (1 – 0) = 3
Jadi, limit dari fungsi f(x) = (3x2 + 2x – 1) / (x2 – 4) saat x mendekati tak hingga adalah 3.
Tabel Sifat-Sifat Limit Tak Hingga Fungsi Aljabar
| Sifat | Rumus | Contoh |
|---|---|---|
| Limit Fungsi Konstan | limx→∞ c = c | limx→∞ 5 = 5 |
| Limit Fungsi Linear | limx→∞ (ax + b) = ∞ jika a > 0 limx→∞ (ax + b) = -∞ jika a < 0 |
limx→∞ (2x + 3) = ∞ limx→∞ (-3x + 1) = -∞ |
| Limit Fungsi Polinomial | limx→∞ (anxn + an-1xn-1 + … + a1x + a0) = ∞ jika an > 0 limx→∞ (anxn + an-1xn-1 + … + a1x + a0) = -∞ jika an < 0 |
limx→∞ (x3 – 2x2 + 5) = ∞ limx→∞ (-2x4 + 3x2 – 1) = -∞ |
| Limit Fungsi Rasional | limx→∞ [f(x) / g(x)] = limx→∞ [(anxn + an-1xn-1 + … + a1x + a0) / (bmxm + bm-1xm-1 + … + b1x + b0)] = limx→∞ [(an + an-1/x + … + a1/xn-1 + a0/xn) / (bm + bm-1/x + … + b1/xm-1 + b0/xm)] |
limx→∞ [(2x2 + 3x – 1) / (x3 – 2x + 5)] = limx→∞ [(2 + 3/x – 1/x2) / (1 – 2/x2 + 5/x3)] = 0 |
Metode Penghitungan Limit Tak Hingga Fungsi Aljabar
Limit tak hingga pada fungsi aljabar adalah konsep yang menggambarkan perilaku fungsi ketika variabel bebas mendekati tak hingga. Penghitungan limit tak hingga ini penting untuk memahami bagaimana fungsi berperilaku pada nilai-nilai ekstrem, seperti pada grafik fungsi. Ada beberapa metode yang dapat digunakan untuk menghitung limit tak hingga fungsi aljabar, dan kita akan membahas beberapa di antaranya.
Metode Faktorisasi
Metode faktorisasi adalah salah satu metode yang umum digunakan untuk menghitung limit tak hingga fungsi aljabar. Metode ini didasarkan pada prinsip bahwa jika kita dapat memfaktorkan fungsi tersebut, kita dapat menyederhanakan fungsi dan kemudian menghitung limitnya. Metode ini efektif untuk fungsi rasional, yaitu fungsi yang merupakan hasil bagi dua polinomial.
- Faktorkan pembilang dan penyebut fungsi.
- Sederhanakan fungsi dengan membagi pembilang dan penyebut dengan faktor yang sama.
- Hitung limit fungsi yang sudah disederhanakan dengan mensubstitusikan nilai tak hingga ke dalam fungsi.
Sebagai contoh, mari kita hitung limit tak hingga fungsi f(x) = (x^2 + 2x – 3) / (x^2 – 1).
limx→∞ (x^2 + 2x – 3) / (x^2 – 1)
Pertama, kita faktorkan pembilang dan penyebut:
limx→∞ [(x + 3)(x – 1)] / [(x + 1)(x – 1)]
Kemudian, kita sederhanakan fungsi dengan membagi pembilang dan penyebut dengan (x – 1):
limx→∞ (x + 3) / (x + 1)
Terakhir, kita hitung limit fungsi yang sudah disederhanakan dengan mensubstitusikan nilai tak hingga ke dalam fungsi:
limx→∞ (x + 3) / (x + 1) = ∞ / ∞ = 1
Jadi, limit tak hingga fungsi f(x) = (x^2 + 2x – 3) / (x^2 – 1) adalah 1.
Metode Pembagian dengan Pangkat Tertinggi
Metode pembagian dengan pangkat tertinggi digunakan untuk menghitung limit tak hingga fungsi rasional dengan membagi pembilang dan penyebut dengan pangkat tertinggi dari variabel bebas. Metode ini efektif ketika fungsi rasional memiliki pangkat tertinggi yang sama pada pembilang dan penyebut.
- Bagilah pembilang dan penyebut dengan pangkat tertinggi dari variabel bebas.
- Hitung limit fungsi yang sudah disederhanakan dengan mensubstitusikan nilai tak hingga ke dalam fungsi.
Sebagai contoh, mari kita hitung limit tak hingga fungsi f(x) = (3x^3 + 2x^2 – 1) / (2x^3 – x + 5).
limx→∞ (3x^3 + 2x^2 – 1) / (2x^3 – x + 5)
Pangkat tertinggi dari variabel bebas adalah x^3. Kita bagi pembilang dan penyebut dengan x^3:
limx→∞ [(3x^3 + 2x^2 – 1) / x^3] / [(2x^3 – x + 5) / x^3]
Kemudian, kita sederhanakan fungsi:
limx→∞ (3 + 2/x – 1/x^3) / (2 – 1/x^2 + 5/x^3)
Terakhir, kita hitung limit fungsi yang sudah disederhanakan dengan mensubstitusikan nilai tak hingga ke dalam fungsi:
limx→∞ (3 + 2/x – 1/x^3) / (2 – 1/x^2 + 5/x^3) = (3 + 0 – 0) / (2 – 0 + 0) = 3/2
Jadi, limit tak hingga fungsi f(x) = (3x^3 + 2x^2 – 1) / (2x^3 – x + 5) adalah 3/2.
Metode L’Hopital
Metode L’Hopital digunakan untuk menghitung limit tak hingga fungsi yang menghasilkan bentuk tak tentu seperti ∞/∞ atau 0/0. Metode ini melibatkan turunan dari pembilang dan penyebut fungsi.
- Hitung turunan dari pembilang dan penyebut fungsi.
- Hitung limit fungsi yang sudah diturunkan dengan mensubstitusikan nilai tak hingga ke dalam fungsi.
Sebagai contoh, mari kita hitung limit tak hingga fungsi f(x) = (e^x – 1) / x.
Nah, kalau kamu lagi belajar tentang contoh soal limit tak hingga fungsi aljabar, pasti kamu juga pengin tahu cara ngerjain soal-soal yang lebih menantang, kan? Misalnya, soal tentang efek Doppler. Efek Doppler ini, seperti yang dibahas di contoh soal un efek doppler , berhubungan dengan perubahan frekuensi gelombang akibat gerak relatif antara sumber gelombang dan pengamat.
Nah, konsep efek Doppler ini bisa dipadukan dengan limit tak hingga fungsi aljabar untuk ngerjain soal-soal yang lebih kompleks, lho!
limx→∞ (e^x – 1) / x
Jika kita substitusikan nilai tak hingga ke dalam fungsi, kita mendapatkan bentuk tak tentu ∞/∞. Kita gunakan metode L’Hopital dengan menghitung turunan dari pembilang dan penyebut:
limx→∞ (e^x – 1) / x = limx→∞ e^x / 1
Kemudian, kita hitung limit fungsi yang sudah diturunkan dengan mensubstitusikan nilai tak hingga ke dalam fungsi:
limx→∞ e^x / 1 = ∞
Jadi, limit tak hingga fungsi f(x) = (e^x – 1) / x adalah ∞.
Aplikasi Limit Tak Hingga Fungsi Aljabar
Limit tak hingga fungsi aljabar, yang membahas perilaku fungsi saat variabel mendekati nilai tak hingga, memiliki aplikasi yang luas dalam berbagai bidang, baik dalam ilmu pengetahuan, teknologi, maupun kehidupan sehari-hari. Konsep ini membantu kita memahami perilaku jangka panjang suatu fungsi, tren, atau pola, dan dapat digunakan untuk membuat prediksi dan mengambil keputusan yang tepat.
Aplikasi Limit Tak Hingga Fungsi Aljabar dalam Kehidupan Sehari-hari
Konsep limit tak hingga fungsi aljabar memiliki aplikasi yang nyata dalam kehidupan sehari-hari, meskipun mungkin tidak selalu tampak langsung. Beberapa contohnya adalah:
- Pertumbuhan Populasi: Model matematika yang digunakan untuk memprediksi pertumbuhan populasi sering kali melibatkan fungsi aljabar. Limit tak hingga dapat digunakan untuk menentukan populasi maksimum yang dapat ditampung oleh suatu wilayah atau sumber daya, memberikan informasi penting untuk perencanaan dan manajemen sumber daya.
- Analisis Ekonomi: Dalam ekonomi, limit tak hingga dapat digunakan untuk menganalisis perilaku jangka panjang dari suatu sistem ekonomi, seperti pertumbuhan ekonomi, inflasi, dan pengangguran. Misalnya, dengan menggunakan limit tak hingga, ekonom dapat memprediksi bagaimana suatu kebijakan ekonomi akan memengaruhi ekonomi dalam jangka panjang.
- Pembuatan Grafik: Dalam pembuatan grafik, limit tak hingga membantu dalam memahami perilaku fungsi saat variabel mendekati nilai tak hingga. Hal ini berguna untuk menentukan asimtot, yaitu garis yang didekati oleh grafik fungsi saat variabel mendekati nilai tak hingga.
Contoh Kasus Penggunaan Limit Tak Hingga Fungsi Aljabar
Berikut adalah contoh kasus yang menunjukkan penggunaan limit tak hingga fungsi aljabar dalam kehidupan sehari-hari:
Misalkan, Anda memiliki perusahaan yang menjual produk tertentu. Anda ingin mengetahui berapa banyak produk yang perlu Anda produksi agar dapat mencapai keuntungan maksimum. Anda memiliki fungsi yang menggambarkan keuntungan perusahaan sebagai fungsi dari jumlah produk yang diproduksi. Dengan menggunakan limit tak hingga, Anda dapat menentukan jumlah produk yang harus diproduksi agar keuntungan perusahaan mendekati nilai maksimum.
Contoh Aplikasi Limit Tak Hingga Fungsi Aljabar di Berbagai Bidang
| Bidang | Contoh Aplikasi |
|---|---|
| Matematika | Menentukan asimtot horizontal dan vertikal pada grafik fungsi |
| Fisika | Menganalisis perilaku benda yang bergerak dengan kecepatan tinggi, seperti roket |
| Kimia | Mempelajari reaksi kimia yang berlangsung dalam waktu lama |
| Biologi | Menganalisis pertumbuhan populasi makhluk hidup |
| Ekonomi | Menganalisis perilaku jangka panjang dari suatu sistem ekonomi |
Contoh Soal Limit Tak Hingga Fungsi Aljabar

Limit tak hingga pada fungsi aljabar adalah konsep yang menarik dalam kalkulus. Konsep ini memungkinkan kita untuk menyelidiki perilaku fungsi saat variabel inputnya mendekati nilai tak hingga. Pada dasarnya, kita ingin mengetahui apa yang terjadi pada nilai fungsi ketika variabel inputnya semakin besar atau semakin kecil tanpa batas.
Fungsi Polinomial
Fungsi polinomial merupakan fungsi yang terdiri dari suku-suku yang melibatkan variabel pangkat bulat non-negatif. Contoh soal limit tak hingga fungsi aljabar yang melibatkan fungsi polinomial:
- Tentukan nilai limit dari fungsi f(x) = 2x3 + 5x2 – 3x + 1 saat x mendekati tak hingga.
Untuk menyelesaikan soal ini, kita dapat melihat bahwa suku dengan pangkat tertinggi pada fungsi tersebut adalah 2x3. Ketika x mendekati tak hingga, suku ini akan mendominasi fungsi dan nilai limitnya akan sama dengan nilai limit dari suku tersebut. Dengan demikian, limit dari f(x) saat x mendekati tak hingga adalah tak hingga.
Fungsi Rasional
Fungsi rasional adalah fungsi yang dibentuk oleh pembagian dua fungsi polinomial. Contoh soal limit tak hingga fungsi aljabar yang melibatkan fungsi rasional:
- Tentukan nilai limit dari fungsi f(x) = (3x2 + 2x – 1) / (x2 – 4) saat x mendekati tak hingga.
Dalam fungsi rasional, untuk menentukan nilai limit saat x mendekati tak hingga, kita dapat membagi pembilang dan penyebut dengan suku dengan pangkat tertinggi pada penyebut. Pada contoh ini, pangkat tertinggi pada penyebut adalah x2. Maka, kita bagi pembilang dan penyebut dengan x2:
f(x) = (3x2 + 2x – 1) / (x2 – 4) = (3 + 2/x – 1/x2) / (1 – 4/x2)
Ketika x mendekati tak hingga, suku-suku yang mengandung x di penyebut akan mendekati nol. Oleh karena itu, limit dari f(x) saat x mendekati tak hingga adalah 3/1 = 3.
Fungsi Trigonometri
Fungsi trigonometri adalah fungsi yang melibatkan sudut-sudut dan sisi-sisi segitiga. Contoh soal limit tak hingga fungsi aljabar yang melibatkan fungsi trigonometri:
- Tentukan nilai limit dari fungsi f(x) = sin(x) / x saat x mendekati tak hingga.
Fungsi sin(x) memiliki nilai yang berosilasi antara -1 dan 1. Ketika x mendekati tak hingga, nilai sin(x) akan tetap berosilasi, tetapi nilai x akan semakin besar. Oleh karena itu, nilai limit dari f(x) saat x mendekati tak hingga adalah 0.
Penyelesaian Soal Limit Tak Hingga Fungsi Aljabar
Limit tak hingga fungsi aljabar adalah konsep yang penting dalam matematika, terutama dalam kalkulus. Konsep ini membahas bagaimana nilai fungsi mendekati suatu nilai tertentu ketika variabel bebasnya mendekati tak hingga. Untuk menyelesaikan soal limit tak hingga fungsi aljabar, kita perlu memahami langkah-langkah yang tepat dan menerapkannya secara sistematis.
Langkah-langkah Menyelesaikan Soal Limit Tak Hingga Fungsi Aljabar
Berikut adalah langkah-langkah umum yang dapat digunakan untuk menyelesaikan soal limit tak hingga fungsi aljabar:
- Faktorkan fungsi aljabar tersebut.
- Sederhanakan fungsi aljabar tersebut dengan membagi setiap suku dengan pangkat tertinggi dari variabel bebasnya.
- Tentukan nilai limit dari fungsi aljabar yang telah disederhanakan ketika variabel bebasnya mendekati tak hingga.
Contoh Soal Limit Tak Hingga Fungsi Aljabar
Misalnya, kita ingin mencari limit dari fungsi berikut ketika x mendekati tak hingga:
limx->∞ (3x2 + 2x – 1) / (x2 – 5)
Berikut adalah langkah-langkah penyelesaiannya:
- Fungsi aljabar tersebut sudah difaktorkan, sehingga kita dapat langsung ke langkah selanjutnya.
- Bagi setiap suku dengan pangkat tertinggi dari variabel bebasnya, yaitu x2:
limx->∞ (3x2/x2 + 2x/x2 – 1/x2) / (x2/x2 – 5/x2)
Sederhanakan:
limx->∞ (3 + 2/x – 1/x2) / (1 – 5/x2)
- Ketika x mendekati tak hingga, nilai 2/x, 1/x2, dan 5/x2 mendekati nol. Sehingga:
limx->∞ (3 + 2/x – 1/x2) / (1 – 5/x2) = (3 + 0 – 0) / (1 – 0) = 3
Jadi, limit dari fungsi (3x2 + 2x – 1) / (x2 – 5) ketika x mendekati tak hingga adalah 3.
Tabel Langkah-langkah Penyelesaian Soal Limit Tak Hingga Fungsi Aljabar
| Langkah | Penjelasan |
|---|---|
| 1. Faktorkan fungsi aljabar tersebut. | Jika fungsi aljabar tersebut dapat difaktorkan, faktorkanlah terlebih dahulu. |
| 2. Sederhanakan fungsi aljabar tersebut dengan membagi setiap suku dengan pangkat tertinggi dari variabel bebasnya. | Tujuannya adalah untuk menghilangkan faktor-faktor yang menyebabkan nilai limit tak hingga. |
| 3. Tentukan nilai limit dari fungsi aljabar yang telah disederhanakan ketika variabel bebasnya mendekati tak hingga. | Setelah fungsi aljabar disederhanakan, substitusikan nilai tak hingga ke dalam fungsi tersebut dan hitung nilainya. |
Penerapan Limit Tak Hingga Fungsi Aljabar dalam Kalkulus: Contoh Soal Limit Tak Hingga Fungsi Aljabar
Limit tak hingga fungsi aljabar merupakan konsep penting dalam kalkulus yang memungkinkan kita untuk menganalisis perilaku fungsi ketika variabel bebasnya mendekati tak hingga. Penerapan limit tak hingga ini meluas ke berbagai konsep kalkulus, khususnya dalam turunan dan integral, serta memberikan pemahaman yang lebih dalam tentang kontinuitas suatu fungsi.
Penerapan Limit Tak Hingga dalam Konsep Turunan
Konsep turunan dalam kalkulus berkaitan dengan laju perubahan suatu fungsi terhadap perubahan variabel bebasnya. Limit tak hingga fungsi aljabar berperan penting dalam menentukan turunan suatu fungsi, terutama dalam kasus-kasus yang melibatkan fungsi polinomial atau fungsi rasional. Misalnya, dalam mencari turunan fungsi polinomial dengan derajat tinggi, limit tak hingga digunakan untuk menentukan perilaku fungsi ketika variabel bebasnya mendekati tak hingga.
- Dalam mencari turunan fungsi polinomial dengan derajat tinggi, limit tak hingga digunakan untuk menentukan perilaku fungsi ketika variabel bebasnya mendekati tak hingga.
- Limit tak hingga juga digunakan dalam menentukan turunan fungsi rasional, di mana limit digunakan untuk menentukan perilaku fungsi ketika variabel bebasnya mendekati tak hingga atau mendekati titik-titik singular.
Penerapan Limit Tak Hingga dalam Konsep Integral
Integral dalam kalkulus digunakan untuk menghitung luas daerah yang dibatasi oleh kurva, sumbu x, dan garis vertikal. Limit tak hingga fungsi aljabar memiliki peran penting dalam menghitung integral tertentu, terutama dalam kasus-kasus yang melibatkan fungsi yang tidak terdefinisi pada titik tertentu atau memiliki perilaku yang tidak teratur pada titik tertentu.
- Limit tak hingga digunakan untuk menghitung integral tertentu, terutama dalam kasus-kasus yang melibatkan fungsi yang tidak terdefinisi pada titik tertentu atau memiliki perilaku yang tidak teratur pada titik tertentu.
- Dalam menghitung integral tak tentu, limit tak hingga digunakan untuk menentukan nilai integral pada batas tak hingga, sehingga kita dapat memahami perilaku fungsi pada batas tak hingga.
Hubungan Limit Tak Hingga Fungsi Aljabar dengan Konsep Kontinuitas
Kontinuitas suatu fungsi berkaitan dengan kelancaran grafik fungsi tersebut. Limit tak hingga fungsi aljabar dapat digunakan untuk menentukan kontinuitas suatu fungsi pada titik tertentu atau pada batas tak hingga.
- Jika limit tak hingga fungsi aljabar pada suatu titik sama dengan nilai fungsi pada titik tersebut, maka fungsi tersebut dikatakan kontinu pada titik tersebut.
- Jika limit tak hingga fungsi aljabar pada batas tak hingga ada, maka fungsi tersebut dikatakan kontinu pada batas tak hingga.
Kesulitan dalam Memahami Limit Tak Hingga Fungsi Aljabar
Konsep limit tak hingga fungsi aljabar merupakan konsep yang penting dalam matematika, khususnya dalam kalkulus. Konsep ini membantu kita memahami perilaku fungsi ketika nilai inputnya mendekati tak hingga. Namun, bagi sebagian siswa, memahami konsep ini bisa menjadi tantangan.
Identifikasi Kesulitan Siswa dalam Memahami Limit Tak Hingga Fungsi Aljabar
Siswa seringkali mengalami kesulitan dalam memahami konsep limit tak hingga fungsi aljabar karena beberapa faktor, antara lain:
- Kesulitan dalam memahami konsep tak hingga itu sendiri. Konsep tak hingga merupakan konsep abstrak yang sulit dibayangkan. Siswa mungkin kesulitan membayangkan nilai yang terus bertambah tanpa batas.
- Kesulitan dalam menghubungkan konsep limit dengan grafik fungsi. Siswa mungkin kesulitan melihat bagaimana limit fungsi dihubungkan dengan perilaku grafik fungsi ketika nilai input mendekati tak hingga.
- Kesulitan dalam memahami konsep limit kiri dan limit kanan. Siswa mungkin kesulitan memahami bagaimana limit fungsi berbeda ketika nilai input mendekati tak hingga dari arah kiri dan kanan.
- Kesulitan dalam menyelesaikan soal-soal limit tak hingga. Siswa mungkin kesulitan dalam menerapkan konsep limit tak hingga dalam menyelesaikan soal-soal yang melibatkan fungsi aljabar.
Strategi Mengatasi Kesulitan Memahami Limit Tak Hingga Fungsi Aljabar
Ada beberapa strategi yang dapat digunakan untuk membantu siswa mengatasi kesulitan dalam memahami konsep limit tak hingga fungsi aljabar:
- Gunakan visualisasi. Visualisasi dapat membantu siswa memahami konsep tak hingga dan menghubungkan konsep limit dengan grafik fungsi. Misalnya, gunakan grafik fungsi untuk menunjukkan bagaimana nilai fungsi mendekati suatu nilai tertentu ketika nilai input mendekati tak hingga.
- Gunakan contoh konkret. Gunakan contoh konkret untuk menjelaskan konsep limit tak hingga. Misalnya, gunakan contoh kecepatan mobil yang semakin cepat ketika mobil melaju di jalan raya.
- Gunakan manipulasi aljabar. Manipulasi aljabar dapat membantu siswa memahami bagaimana limit fungsi dapat dihitung. Misalnya, gunakan manipulasi aljabar untuk menyederhanakan fungsi sebelum menghitung limitnya.
- Gunakan latihan soal. Latihan soal dapat membantu siswa mengasah pemahaman mereka tentang konsep limit tak hingga. Berikan soal-soal yang beragam, mulai dari soal-soal dasar hingga soal-soal yang lebih menantang.
Contoh Soal yang Sering Menimbulkan Kesulitan
Berikut adalah contoh soal yang sering menimbulkan kesulitan bagi siswa:
Tentukan limit dari fungsi f(x) = (x^2 + 2x) / (x – 1) ketika x mendekati tak hingga.
Untuk menyelesaikan soal ini, siswa perlu memahami bahwa ketika x mendekati tak hingga, nilai x^2 akan jauh lebih besar dibandingkan dengan nilai 2x. Oleh karena itu, kita dapat menyederhanakan fungsi f(x) dengan membagi kedua ruas dengan x^2.
f(x) = (x^2 + 2x) / (x – 1) = (1 + 2/x) / (1/x – 1/x^2)
Ketika x mendekati tak hingga, nilai 1/x dan 1/x^2 akan mendekati 0. Oleh karena itu, limit dari fungsi f(x) ketika x mendekati tak hingga adalah:
lim x->∞ f(x) = lim x->∞ (1 + 2/x) / (1/x – 1/x^2) = (1 + 0) / (0 – 0) = 1/0 = ∞
Jadi, limit dari fungsi f(x) = (x^2 + 2x) / (x – 1) ketika x mendekati tak hingga adalah tak hingga.
Aplikasi Limit Tak Hingga Fungsi Aljabar dalam Bidang Lain
Limit tak hingga fungsi aljabar memiliki aplikasi yang luas dalam berbagai bidang, seperti fisika, ekonomi, dan teknik. Penerapannya dalam bidang-bidang ini memungkinkan kita untuk menganalisis dan memahami perilaku sistem atau fenomena yang kompleks.
Aplikasi dalam Fisika
Dalam fisika, limit tak hingga fungsi aljabar digunakan untuk memahami perilaku objek yang bergerak dengan kecepatan tinggi atau pada skala yang sangat kecil. Contohnya, dalam mekanika kuantum, limit tak hingga digunakan untuk menghitung probabilitas keberadaan partikel dalam suatu ruang tertentu.
- Limit tak hingga digunakan untuk menentukan energi kinetik suatu objek yang bergerak dengan kecepatan mendekati kecepatan cahaya.
- Dalam teori relativitas, limit tak hingga digunakan untuk menghitung energi dan momentum partikel yang bergerak dengan kecepatan mendekati kecepatan cahaya.
- Limit tak hingga juga digunakan dalam teori gravitasi untuk memahami perilaku medan gravitasi pada jarak yang sangat jauh.
Aplikasi dalam Ekonomi
Dalam ekonomi, limit tak hingga fungsi aljabar digunakan untuk menganalisis perilaku pasar dan pertumbuhan ekonomi. Contohnya, limit tak hingga digunakan untuk menghitung pertumbuhan ekonomi jangka panjang.
- Limit tak hingga digunakan untuk menganalisis perilaku pasar saham, seperti menghitung harga saham yang akan dicapai dalam jangka waktu yang sangat lama.
- Limit tak hingga digunakan untuk menghitung pertumbuhan ekonomi jangka panjang, dengan mengasumsikan bahwa faktor-faktor yang memengaruhi pertumbuhan ekonomi akan terus berlanjut dalam jangka waktu yang sangat lama.
- Limit tak hingga juga digunakan untuk menganalisis perilaku konsumen dan perusahaan dalam jangka waktu yang sangat lama.
Aplikasi dalam Teknik
Dalam teknik, limit tak hingga fungsi aljabar digunakan untuk merancang dan menganalisis sistem yang kompleks, seperti struktur bangunan, jaringan listrik, dan sistem kontrol. Contohnya, limit tak hingga digunakan untuk menghitung kekuatan struktur bangunan.
- Limit tak hingga digunakan untuk menghitung kekuatan struktur bangunan, seperti jembatan dan gedung tinggi, dengan mengasumsikan bahwa beban yang bekerja pada struktur akan terus meningkat dalam jangka waktu yang sangat lama.
- Limit tak hingga digunakan untuk menganalisis perilaku sistem kontrol, seperti sistem kontrol suhu dan sistem kontrol kecepatan, dengan mengasumsikan bahwa sistem tersebut akan terus beroperasi dalam jangka waktu yang sangat lama.
- Limit tak hingga juga digunakan untuk merancang sistem komunikasi, seperti jaringan nirkabel dan jaringan kabel, dengan mengasumsikan bahwa jumlah pengguna akan terus meningkat dalam jangka waktu yang sangat lama.
| Bidang | Contoh Aplikasi Limit Tak Hingga Fungsi Aljabar |
|---|---|
| Fisika | Menghitung energi kinetik objek yang bergerak dengan kecepatan mendekati kecepatan cahaya, menghitung energi dan momentum partikel dalam teori relativitas, memahami perilaku medan gravitasi pada jarak yang sangat jauh. |
| Ekonomi | Menganalisis perilaku pasar saham, menghitung pertumbuhan ekonomi jangka panjang, menganalisis perilaku konsumen dan perusahaan dalam jangka waktu yang sangat lama. |
| Teknik | Menghitung kekuatan struktur bangunan, menganalisis perilaku sistem kontrol, merancang sistem komunikasi. |
Pengembangan Soal Limit Tak Hingga Fungsi Aljabar
Membuat soal limit tak hingga fungsi aljabar yang menantang dan kreatif adalah kunci untuk meningkatkan pemahaman siswa dan mendorong mereka berpikir kritis. Soal yang baik tidak hanya menguji kemampuan menghitung, tetapi juga mendorong siswa untuk memahami konsep limit tak hingga dalam konteks yang lebih luas.
Soal Menantang dan Kreatif
Untuk menciptakan soal limit tak hingga fungsi aljabar yang menantang dan kreatif, pertimbangkan beberapa aspek berikut:
- Tingkat Kesulitan: Soal dapat dirancang dengan tingkat kesulitan yang bervariasi, mulai dari soal dasar hingga soal yang lebih kompleks. Untuk soal yang lebih menantang, pertimbangkan penggunaan fungsi-fungsi yang lebih rumit, manipulasi aljabar yang lebih kompleks, atau kombinasi dari keduanya.
- Konteks Soal: Buatlah soal yang relevan dengan kehidupan nyata atau bidang studi lainnya. Misalnya, soal tentang pertumbuhan populasi, laju reaksi kimia, atau pergerakan benda dapat membuat siswa lebih tertarik dan termotivasi.
- Strategi Penyelesaian: Soal dapat dirancang agar siswa menggunakan berbagai strategi penyelesaian, seperti manipulasi aljabar, pemfaktoran, atau teorema limit. Ini membantu siswa mengembangkan pemahaman yang lebih komprehensif tentang konsep limit tak hingga.
Aplikasi dalam Kehidupan Nyata
Limit tak hingga fungsi aljabar memiliki aplikasi yang luas dalam kehidupan nyata, seperti:
- Pertumbuhan Populasi: Model matematika untuk pertumbuhan populasi sering kali melibatkan fungsi eksponensial yang memiliki limit tak hingga.
- Laju Reaksi Kimia: Laju reaksi kimia dapat dimodelkan dengan fungsi yang memiliki limit tak hingga, yang menunjukkan bahwa reaksi akan berlanjut hingga semua reaktan habis.
- Pergerakan Benda: Gerakan benda seperti peluru atau roket dapat dimodelkan dengan fungsi yang memiliki limit tak hingga, yang menunjukkan kecepatan maksimum yang dapat dicapai benda tersebut.
Strategi untuk Membuat Soal yang Lebih Menarik dan Bermakna
Berikut adalah beberapa strategi untuk membuat soal limit tak hingga fungsi aljabar yang lebih menarik dan bermakna:
- Gunakan Gambar dan Diagram: Gambar dan diagram dapat membantu siswa memvisualisasikan konsep limit tak hingga dan membuat soal lebih menarik.
- Tawarkan Pilihan Ganda: Soal pilihan ganda dapat mendorong siswa untuk berpikir kritis dan memilih jawaban yang tepat.
- Buat Soal Bersifat Investigatif: Soal investigatif mendorong siswa untuk mengeksplorasi konsep limit tak hingga secara lebih mendalam dan menemukan jawabannya sendiri.
Akhir Kata
Memahami limit tak hingga fungsi aljabar membuka pintu bagi pemahaman yang lebih dalam tentang matematika dan aplikasinya dalam kehidupan nyata. Dari dunia fisika hingga ekonomi, konsep ini menjadi dasar bagi banyak teori dan model. Dengan mempelajari contoh soal dan memahami langkah-langkah penyelesaiannya, Anda akan dapat menguasai konsep ini dan mengaplikasikannya dalam berbagai bidang.