Contoh soal luas permukaan bangun ruang – Pernahkah kamu membayangkan bagaimana cara menghitung luas permukaan kotak kado atau kaleng minuman? Nah, dalam dunia matematika, hal ini dipelajari dalam konsep luas permukaan bangun ruang. Luas permukaan bangun ruang adalah jumlah luas semua sisi yang membentuk bangun ruang tersebut. Misalnya, luas permukaan kubus adalah jumlah luas keenam sisinya yang berbentuk persegi.
Mempelajari luas permukaan bangun ruang tidak hanya penting untuk memahami konsep matematika, tetapi juga bermanfaat dalam kehidupan sehari-hari. Bayangkan, kamu ingin mengecat dinding rumah, kamu perlu menghitung luas permukaan dindingnya terlebih dahulu. Atau, kamu ingin membuat kerangka model pesawat terbang, kamu perlu mengetahui luas permukaan setiap bagiannya. Jadi, siap untuk menjelajahi dunia luas permukaan bangun ruang?
Pengertian Luas Permukaan Bangun Ruang
Luas permukaan bangun ruang adalah total luas seluruh sisi atau permukaan yang membatasi bangun ruang tersebut. Bayangkan kamu memiliki sebuah kotak kado, luas permukaan kotak kado itu adalah penjumlahan dari luas semua sisi kotak, termasuk bagian atas, bawah, depan, belakang, kanan, dan kiri.
Jenis-Jenis Bangun Ruang dan Rumus Luas Permukaan
Ada berbagai jenis bangun ruang dengan rumus luas permukaan yang berbeda-beda. Berikut adalah beberapa jenis bangun ruang dan rumus luas permukaannya:
| Jenis Bangun Ruang | Rumus Luas Permukaan |
|---|---|
| Kubus | 6 x s2 |
| Balok | 2 x (p x l + p x t + l x t) |
| Prisma Segitiga | 2 x (luas alas) + (keliling alas x tinggi prisma) |
| Limas Segitiga | (luas alas) + (1/2 x keliling alas x tinggi limas) |
| Bola | 4 x π x r2 |
| Tabung | 2 x π x r x (r + t) |
| Kerucut | π x r x (r + s) |
Rumus Luas Permukaan Bangun Ruang
Luas permukaan bangun ruang adalah jumlah luas semua sisi atau permukaan yang membatasi bangun ruang tersebut. Menghitung luas permukaan bangun ruang sangat penting dalam berbagai bidang, seperti arsitektur, desain interior, dan manufaktur. Dengan memahami cara menghitung luas permukaan, kita dapat menentukan jumlah bahan yang dibutuhkan untuk membangun suatu objek, menghitung biaya produksi, atau bahkan mendesain objek yang efisien dan optimal.
Kubus
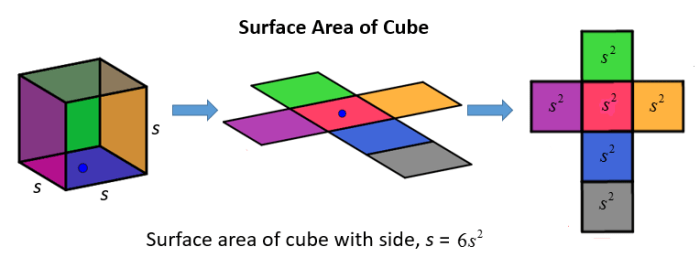
Kubus adalah bangun ruang yang memiliki enam sisi berbentuk persegi dengan ukuran yang sama. Luas permukaan kubus dapat dihitung dengan rumus:
Luas Permukaan Kubus = 6 x sisi x sisi
Contoh soal:
Hitunglah luas permukaan kubus dengan panjang sisi 5 cm.
Penyelesaian:
Luas Permukaan Kubus = 6 x sisi x sisi
Luas Permukaan Kubus = 6 x 5 cm x 5 cm
Luas Permukaan Kubus = 150 cm2
Balok
Balok adalah bangun ruang yang memiliki enam sisi berbentuk persegi panjang dengan ukuran yang berbeda. Luas permukaan balok dapat dihitung dengan rumus:
Luas Permukaan Balok = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
Contoh soal:
Hitunglah luas permukaan balok dengan panjang 10 cm, lebar 5 cm, dan tinggi 3 cm.
Penyelesaian:
Luas Permukaan Balok = 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi)
Luas Permukaan Balok = 2 x (10 cm x 5 cm + 10 cm x 3 cm + 5 cm x 3 cm)
Luas Permukaan Balok = 2 x (50 cm2 + 30 cm2 + 15 cm2)
Luas Permukaan Balok = 2 x 95 cm2
Luas Permukaan Balok = 190 cm2
Prisma
Prisma adalah bangun ruang yang memiliki dua sisi sejajar yang kongruen dan berbentuk poligon, serta sisi-sisi lainnya berbentuk persegi panjang. Luas permukaan prisma dapat dihitung dengan rumus:
Luas Permukaan Prisma = 2 x Luas Alas + Luas Sisi Tegak
Contoh soal:
Hitunglah luas permukaan prisma segitiga dengan alas segitiga siku-siku dengan panjang sisi 3 cm, 4 cm, dan 5 cm, serta tinggi prisma 8 cm.
Penyelesaian:
Luas Alas = 1/2 x alas x tinggi = 1/2 x 3 cm x 4 cm = 6 cm2
Luas Sisi Tegak = keliling alas x tinggi prisma = (3 cm + 4 cm + 5 cm) x 8 cm = 96 cm2
Luas Permukaan Prisma = 2 x Luas Alas + Luas Sisi Tegak
Luas Permukaan Prisma = 2 x 6 cm2 + 96 cm2
Luas Permukaan Prisma = 12 cm2 + 96 cm2
Luas Permukaan Prisma = 108 cm2
Limas
Limas adalah bangun ruang yang memiliki alas berbentuk poligon dan sisi-sisi lainnya berbentuk segitiga yang bertemu pada satu titik puncak. Luas permukaan limas dapat dihitung dengan rumus:
Luas Permukaan Limas = Luas Alas + Jumlah Luas Sisi Tegak
Contoh soal:
Hitunglah luas permukaan limas segiempat beraturan dengan panjang sisi alas 6 cm dan tinggi limas 4 cm.
Penyelesaian:
Luas Alas = sisi x sisi = 6 cm x 6 cm = 36 cm2
Tinggi Sisi Tegak = √(tinggi limas2 + (1/2 x sisi alas)2) = √(4 cm2 + (1/2 x 6 cm)2) = √(4 cm2 + 9 cm2) = √13 cm
Luas Sisi Tegak = 1/2 x alas x tinggi = 1/2 x 6 cm x √13 cm = 3√13 cm2
Luas Permukaan Limas = Luas Alas + Jumlah Luas Sisi Tegak
Luas Permukaan Limas = 36 cm2 + 4 x 3√13 cm2
Luas Permukaan Limas = 36 cm2 + 12√13 cm2
Tabung
Tabung adalah bangun ruang yang memiliki dua sisi sejajar berbentuk lingkaran dan sisi lainnya berbentuk persegi panjang yang melingkar. Luas permukaan tabung dapat dihitung dengan rumus:
Luas Permukaan Tabung = 2 x Luas Alas + Luas Sisi Tegak
Contoh soal:
Hitunglah luas permukaan tabung dengan jari-jari alas 7 cm dan tinggi tabung 10 cm.
Penyelesaian:
Luas Alas = π x jari-jari2 = π x 7 cm x 7 cm = 49π cm2
Luas Sisi Tegak = keliling alas x tinggi tabung = 2π x jari-jari x tinggi tabung = 2π x 7 cm x 10 cm = 140π cm2
Luas Permukaan Tabung = 2 x Luas Alas + Luas Sisi Tegak
Luas Permukaan Tabung = 2 x 49π cm2 + 140π cm2
Luas Permukaan Tabung = 98π cm2 + 140π cm2
Luas Permukaan Tabung = 238π cm2
Kerucut
Kerucut adalah bangun ruang yang memiliki alas berbentuk lingkaran dan sisi lainnya berbentuk segitiga yang melingkar. Luas permukaan kerucut dapat dihitung dengan rumus:
Luas Permukaan Kerucut = Luas Alas + Luas Sisi Tegak
Contoh soal:
Hitunglah luas permukaan kerucut dengan jari-jari alas 5 cm dan garis pelukis 13 cm.
Penyelesaian:
Luas Alas = π x jari-jari2 = π x 5 cm x 5 cm = 25π cm2
Luas Sisi Tegak = π x jari-jari x garis pelukis = π x 5 cm x 13 cm = 65π cm2
Luas Permukaan Kerucut = Luas Alas + Luas Sisi Tegak
Luas Permukaan Kerucut = 25π cm2 + 65π cm2
Luas Permukaan Kerucut = 90π cm2
Bola
Bola adalah bangun ruang yang berbentuk bulat sempurna. Luas permukaan bola dapat dihitung dengan rumus:
Luas Permukaan Bola = 4 x π x jari-jari2
Contoh soal:
Hitunglah luas permukaan bola dengan jari-jari 6 cm.
Penyelesaian:
Luas Permukaan Bola = 4 x π x jari-jari2
Luas Permukaan Bola = 4 x π x 6 cm x 6 cm
Luas Permukaan Bola = 144π cm2
Penerapan Luas Permukaan Bangun Ruang dalam Kehidupan Sehari-hari
Luas permukaan bangun ruang merupakan konsep yang sering kita jumpai dalam kehidupan sehari-hari. Konsep ini membantu kita dalam menghitung luas bidang yang menutupi suatu bangun ruang, seperti dinding rumah, kaleng, dan lain sebagainya.
Contoh Penggunaan Luas Permukaan Bangun Ruang
Penerapan luas permukaan bangun ruang sangat luas dan membantu kita dalam berbagai aktivitas. Berikut beberapa contohnya:
- Menghitung luas permukaan dinding rumah: Saat ingin mengecat rumah, kita perlu mengetahui luas permukaan dinding untuk menghitung kebutuhan cat. Rumus yang digunakan adalah luas permukaan persegi panjang (panjang x lebar) untuk dinding yang berbentuk persegi panjang dan luas permukaan segitiga (1/2 x alas x tinggi) untuk dinding yang berbentuk segitiga.
- Menghitung luas permukaan kaleng: Dalam industri makanan dan minuman, luas permukaan kaleng penting untuk menghitung kebutuhan bahan baku dan desain kemasan. Rumus yang digunakan adalah luas permukaan tabung (2πr² + 2πrt) di mana r adalah jari-jari alas dan t adalah tinggi tabung.
- Menghitung luas permukaan bola: Bola digunakan dalam berbagai bidang seperti olahraga, mainan, dan industri. Rumus yang digunakan adalah luas permukaan bola (4πr²) di mana r adalah jari-jari bola.
- Menghitung luas permukaan kerucut: Kerucut sering digunakan dalam berbagai desain seperti topi, corong, dan wadah. Rumus yang digunakan adalah luas permukaan kerucut (πr² + πrs) di mana r adalah jari-jari alas, s adalah garis pelukis kerucut.
Tabel Contoh Penggunaan Luas Permukaan Bangun Ruang
| Contoh Penggunaan | Bangun Ruang | Rumus |
|---|---|---|
| Menghitung luas permukaan dinding rumah | Kubus, Balok | Luas Permukaan Kubus = 6s² (s = sisi kubus) Luas Permukaan Balok = 2(pl + pt + lt) (p = panjang, l = lebar, t = tinggi) |
| Menghitung luas permukaan kaleng | Tabung | Luas Permukaan Tabung = 2πr² + 2πrt (r = jari-jari alas, t = tinggi tabung) |
| Menghitung luas permukaan bola | Bola | Luas Permukaan Bola = 4πr² (r = jari-jari bola) |
| Menghitung luas permukaan kerucut | Kerucut | Luas Permukaan Kerucut = πr² + πrs (r = jari-jari alas, s = garis pelukis kerucut) |
Ilustrasi Penggunaan Luas Permukaan Bangun Ruang
Bayangkan sebuah kotak kado berbentuk kubus. Untuk membungkus kotak kado tersebut, kita perlu menghitung luas permukaannya agar kertas kado yang kita gunakan cukup. Luas permukaan kubus dihitung dengan rumus 6s², di mana s adalah panjang sisi kubus. Dengan mengetahui luas permukaannya, kita dapat membeli kertas kado yang sesuai dan membungkus kotak kado dengan rapi.
Soal Latihan Luas Permukaan Bangun Ruang
Setelah memahami rumus dan contoh perhitungan luas permukaan bangun ruang, saatnya untuk menguji pemahamanmu dengan mengerjakan soal latihan. Soal-soal berikut ini akan membantumu mengasah kemampuan dalam menghitung luas permukaan berbagai bangun ruang.
Soal Latihan Tingkat Kesulitan Sedang
Berikut ini adalah 5 soal latihan luas permukaan bangun ruang dengan tingkat kesulitan sedang:
- Sebuah kubus memiliki panjang rusuk 8 cm. Hitunglah luas permukaan kubus tersebut!
- Sebuah balok memiliki panjang 12 cm, lebar 8 cm, dan tinggi 6 cm. Hitunglah luas permukaan balok tersebut!
- Sebuah limas segitiga memiliki panjang alas 10 cm, tinggi alas 6 cm, dan tinggi limas 8 cm. Hitunglah luas permukaan limas segitiga tersebut!
- Sebuah kerucut memiliki jari-jari alas 7 cm dan tinggi 10 cm. Hitunglah luas permukaan kerucut tersebut!
- Sebuah tabung memiliki jari-jari alas 5 cm dan tinggi 12 cm. Hitunglah luas permukaan tabung tersebut!
Jawaban dan Pembahasan Soal Latihan Tingkat Kesulitan Sedang
Berikut adalah jawaban dan pembahasan untuk setiap soal latihan tingkat kesulitan sedang:
-
Diketahui:
- Panjang rusuk kubus = 8 cm
Ditanya:
- Luas permukaan kubus = …?
Jawab:
- Luas permukaan kubus = 6 x (sisi x sisi) = 6 x (8 cm x 8 cm) = 6 x 64 cm2 = 384 cm2
Jadi, luas permukaan kubus tersebut adalah 384 cm2.
-
Diketahui:
- Panjang balok = 12 cm
- Lebar balok = 8 cm
- Tinggi balok = 6 cm
Ditanya:
- Luas permukaan balok = …?
Jawab:
- Luas permukaan balok = 2 x ((panjang x lebar) + (panjang x tinggi) + (lebar x tinggi))
- Luas permukaan balok = 2 x ((12 cm x 8 cm) + (12 cm x 6 cm) + (8 cm x 6 cm))
- Luas permukaan balok = 2 x (96 cm2 + 72 cm2 + 48 cm2)
- Luas permukaan balok = 2 x 216 cm2 = 432 cm2
Jadi, luas permukaan balok tersebut adalah 432 cm2.
Latihan soal luas permukaan bangun ruang bisa jadi seru, lho! Kayak menghitung luas permukaan kubus, misalnya. Tapi, kalau kamu ingin tantangan yang lebih menantang, coba deh cari tahu tentang teori Irving Fisher! Teori ini membahas tentang hubungan antara tingkat bunga dan nilai uang.
Nah, buat kamu yang ingin mendalami teori ini, bisa cek contoh soalnya di contoh soal teori irving fisher. Setelah memahami teori ini, kamu pasti lebih siap menghadapi soal-soal luas permukaan bangun ruang, kan?
-
Diketahui:
- Panjang alas limas segitiga = 10 cm
- Tinggi alas limas segitiga = 6 cm
- Tinggi limas = 8 cm
Ditanya:
- Luas permukaan limas segitiga = …?
Jawab:
- Luas alas limas segitiga = 1/2 x alas x tinggi = 1/2 x 10 cm x 6 cm = 30 cm2
- Luas segitiga tegak limas = 1/2 x alas x tinggi = 1/2 x 10 cm x √(82 + 32) cm = 1/2 x 10 cm x √(73) cm = 5√(73) cm2
- Luas permukaan limas segitiga = Luas alas + 3 x Luas segitiga tegak = 30 cm2 + 3 x 5√(73) cm2 = (30 + 15√(73)) cm2
Jadi, luas permukaan limas segitiga tersebut adalah (30 + 15√(73)) cm2.
-
Diketahui:
- Jari-jari alas kerucut = 7 cm
- Tinggi kerucut = 10 cm
Ditanya:
- Luas permukaan kerucut = …?
Jawab:
- Garis pelukis kerucut = √(jari-jari2 + tinggi2) = √(72 + 102) cm = √(149) cm
- Luas permukaan kerucut = π x jari-jari x (jari-jari + garis pelukis) = π x 7 cm x (7 cm + √(149) cm) = 7π(7 + √(149)) cm2
Jadi, luas permukaan kerucut tersebut adalah 7π(7 + √(149)) cm2.
-
Diketahui:
- Jari-jari alas tabung = 5 cm
- Tinggi tabung = 12 cm
Ditanya:
- Luas permukaan tabung = …?
Jawab:
- Luas permukaan tabung = 2 x π x jari-jari x (jari-jari + tinggi) = 2 x π x 5 cm x (5 cm + 12 cm) = 10π x 17 cm2 = 170π cm2
Jadi, luas permukaan tabung tersebut adalah 170π cm2.
Soal Latihan Tingkat Kesulitan Tinggi
Berikut ini adalah 2 soal latihan luas permukaan bangun ruang dengan tingkat kesulitan tinggi:
- Sebuah limas segi empat beraturan memiliki panjang sisi alas 10 cm dan tinggi limas 12 cm. Hitunglah luas permukaan limas segi empat beraturan tersebut!
- Sebuah bola memiliki diameter 14 cm. Hitunglah luas permukaan bola tersebut!
Jawaban dan Pembahasan Soal Latihan Tingkat Kesulitan Tinggi
Berikut adalah jawaban dan pembahasan untuk setiap soal latihan tingkat kesulitan tinggi:
-
Diketahui:
- Panjang sisi alas limas segi empat beraturan = 10 cm
- Tinggi limas = 12 cm
Ditanya:
- Luas permukaan limas segi empat beraturan = …?
Jawab:
- Luas alas limas segi empat beraturan = sisi x sisi = 10 cm x 10 cm = 100 cm2
- Tinggi segitiga tegak limas = √(tinggi limas2 + (1/2 x sisi alas)2) = √(122 + (1/2 x 10)2) cm = √(169) cm = 13 cm
- Luas segitiga tegak limas = 1/2 x alas x tinggi = 1/2 x 10 cm x 13 cm = 65 cm2
- Luas permukaan limas segi empat beraturan = Luas alas + 4 x Luas segitiga tegak = 100 cm2 + 4 x 65 cm2 = 360 cm2
Jadi, luas permukaan limas segi empat beraturan tersebut adalah 360 cm2.
-
Diketahui:
- Diameter bola = 14 cm
Ditanya:
- Luas permukaan bola = …?
Jawab:
- Jari-jari bola = diameter / 2 = 14 cm / 2 = 7 cm
- Luas permukaan bola = 4 x π x jari-jari2 = 4 x π x 7 cm2 = 196π cm2
Jadi, luas permukaan bola tersebut adalah 196π cm2.
Tips dan Trik Menghitung Luas Permukaan Bangun Ruang
Menghitung luas permukaan bangun ruang memang terlihat rumit, tapi sebenarnya bisa dipecah menjadi langkah-langkah sederhana. Dengan memahami konsep dasar dan beberapa tips dan trik, kamu bisa menghitung luas permukaan bangun ruang dengan lebih mudah dan cepat.
Membagi Bangun Ruang Menjadi Bentuk Sederhana
Salah satu cara untuk mempermudah perhitungan luas permukaan adalah dengan membagi bangun ruang menjadi bentuk-bentuk sederhana yang sudah kamu kenal. Misalnya, kubus dapat dibagi menjadi 6 persegi, balok menjadi 6 persegi panjang, dan limas menjadi segitiga dan persegi.
Memahami Rumus Luas Permukaan, Contoh soal luas permukaan bangun ruang
Pastikan kamu memahami rumus luas permukaan setiap bangun ruang. Misalnya, luas permukaan kubus adalah 6 kali luas sisi perseginya, sedangkan luas permukaan balok adalah 2 kali (panjang x lebar + panjang x tinggi + lebar x tinggi).
Menggunakan Tabel Rumus
Membuat tabel rumus luas permukaan setiap bangun ruang dapat membantu kamu mengingat dan mengakses rumus dengan cepat. Berikut contoh tabel rumus luas permukaan bangun ruang:
| Bangun Ruang | Rumus Luas Permukaan |
|---|---|
| Kubus | 6 x sisi² |
| Balok | 2 x (panjang x lebar + panjang x tinggi + lebar x tinggi) |
| Prisma Segitiga | 2 x (luas alas + luas sisi tegak) |
| Limas Segi Empat | (luas alas + luas sisi tegak) |
Memanfaatkan Sisi-Sisi yang Sama
Perhatikan dengan cermat bentuk bangun ruang. Kadang, beberapa sisi bangun ruang memiliki luas yang sama. Misalnya, pada kubus, keenam sisinya memiliki luas yang sama. Manfaatkan hal ini untuk mempercepat perhitungan luas permukaan.
Contoh Soal dan Penyelesaian
Misalnya, kita ingin menghitung luas permukaan sebuah kubus dengan panjang sisi 5 cm.
1. Kita tahu bahwa luas permukaan kubus adalah 6 x sisi².
2. Kita substitusikan nilai sisi dengan 5 cm, sehingga luas permukaan kubus = 6 x 5² = 6 x 25 = 150 cm².
Jadi, luas permukaan kubus tersebut adalah 150 cm².
Aplikasi Luas Permukaan Bangun Ruang dalam Bidang Lain
Luas permukaan bangun ruang memiliki aplikasi yang luas dalam berbagai bidang, tidak hanya dalam matematika tetapi juga dalam kehidupan sehari-hari. Pengetahuan tentang luas permukaan bangun ruang dapat membantu dalam menyelesaikan masalah praktis dan memecahkan tantangan di berbagai bidang, seperti arsitektur, teknik, dan seni.
Arsitektur
Dalam arsitektur, luas permukaan bangun ruang sangat penting dalam perencanaan dan desain bangunan. Menghitung luas permukaan atap, dinding, dan lantai sangat penting untuk menentukan kebutuhan material, seperti atap, cat, dan keramik, serta untuk memperkirakan biaya konstruksi.
- Menghitung luas permukaan atap: Arsitek perlu menghitung luas permukaan atap untuk menentukan jumlah material yang dibutuhkan untuk membangun atap, seperti genteng, kayu, dan asbes. Informasi ini juga berguna untuk menghitung biaya pemasangan atap dan memperkirakan waktu yang dibutuhkan untuk menyelesaikannya.
- Menghitung luas permukaan dinding: Menghitung luas permukaan dinding penting untuk menentukan jumlah cat, wallpaper, atau material pelapis dinding yang dibutuhkan. Informasi ini juga dapat membantu dalam menentukan jumlah tenaga kerja yang dibutuhkan untuk mengecat atau melapisi dinding.
- Menghitung luas permukaan lantai: Arsitek perlu menghitung luas permukaan lantai untuk menentukan jumlah material yang dibutuhkan untuk membangun lantai, seperti keramik, kayu, atau marmer. Informasi ini juga berguna untuk menghitung biaya pemasangan lantai dan memperkirakan waktu yang dibutuhkan untuk menyelesaikannya.
Teknik
Dalam teknik, luas permukaan bangun ruang digunakan dalam berbagai aplikasi, termasuk dalam konstruksi, desain mesin, dan manufaktur. Menghitung luas permukaan benda-benda yang digunakan dalam konstruksi, seperti balok, kolom, dan plat, penting untuk menentukan kekuatan dan stabilitas struktur. Luas permukaan mesin juga penting untuk menghitung efisiensi perpindahan panas dan untuk menentukan jumlah pelumas yang dibutuhkan.
- Menghitung luas permukaan benda-benda konstruksi: Insinyur sipil menggunakan luas permukaan untuk menghitung beban yang dapat ditanggung oleh struktur, seperti jembatan, gedung, dan bendungan. Informasi ini penting untuk memastikan keamanan dan stabilitas struktur.
- Menghitung luas permukaan mesin: Insinyur mekanik menggunakan luas permukaan untuk menghitung perpindahan panas pada mesin, seperti mesin mobil dan mesin industri. Informasi ini penting untuk memastikan efisiensi dan kinerja mesin.
- Menghitung luas permukaan dalam manufaktur: Luas permukaan digunakan dalam proses manufaktur, seperti pengecatan, pelapisan, dan pencetakan. Informasi ini penting untuk menentukan jumlah material yang dibutuhkan dan untuk memastikan kualitas produk akhir.
Seni
Dalam seni, luas permukaan bangun ruang dapat digunakan untuk menghitung luas permukaan objek seni, seperti patung, lukisan, dan instalasi. Informasi ini dapat membantu seniman dalam menentukan jumlah material yang dibutuhkan, seperti cat, tanah liat, atau kayu, serta untuk memperkirakan biaya produksi.
- Menghitung luas permukaan objek seni: Seniman patung dapat menggunakan luas permukaan untuk menghitung jumlah tanah liat, kayu, atau logam yang dibutuhkan untuk membuat patung. Informasi ini juga dapat membantu dalam menentukan biaya produksi patung.
- Menghitung luas permukaan lukisan: Pelukis dapat menggunakan luas permukaan untuk menentukan jumlah cat yang dibutuhkan untuk melukis kanvas. Informasi ini juga dapat membantu dalam menentukan biaya produksi lukisan.
- Menghitung luas permukaan instalasi: Seniman instalasi dapat menggunakan luas permukaan untuk menghitung jumlah material yang dibutuhkan untuk membuat instalasi. Informasi ini juga dapat membantu dalam menentukan biaya produksi instalasi.
Simpulan Akhir: Contoh Soal Luas Permukaan Bangun Ruang
Memahami konsep luas permukaan bangun ruang membuka pintu untuk menyelesaikan berbagai permasalahan di kehidupan nyata. Mulai dari menghitung luas permukaan rumah hingga menghitung luas permukaan benda-benda di sekitar kita. Dengan latihan yang cukup, kamu akan semakin mahir dalam menguasai konsep ini dan dapat menerapkannya dalam berbagai situasi.