Contoh Soal Matematika dan Jawabannya: Latihan Menaklukkan Dunia Angka

Contoh soal matematika dan jawabannya – Matematika, pelajaran yang seringkali dianggap menakutkan, ternyata bisa menjadi teman setia dalam memahami dunia. Dari menghitung jumlah apel di keranjang hingga merancang pesawat luar angkasa, matematika hadir dalam berbagai aspek kehidupan. Nah, untuk membantu Anda menaklukkan dunia angka, berikut adalah kumpulan contoh soal matematika beserta jawabannya yang disusun berdasarkan jenis, tingkat kesulitan, dan formatnya.

Siap-siap untuk berpetualang dalam dunia angka! Di sini, Anda akan menemukan contoh soal matematika yang menarik dan menantang, mulai dari soal dasar hingga soal yang lebih kompleks. Dengan mempelajari contoh-contoh soal ini, Anda akan memahami konsep matematika dengan lebih baik dan mengasah kemampuan berpikir logis Anda.

Jenis Soal Matematika

Matematika merupakan ilmu yang mempelajari tentang angka, struktur, ruang, dan perubahan. Bidang ini memiliki cakupan yang luas dan dibagi menjadi berbagai cabang, seperti aljabar, geometri, kalkulus, dan statistika. Setiap cabang memiliki konsep dan metode penyelesaian yang berbeda. Artikel ini akan membahas contoh soal matematika untuk setiap cabang tersebut, disertai jawabannya.

Aljabar

Aljabar adalah cabang matematika yang mempelajari tentang variabel, persamaan, dan fungsi. Dalam aljabar, simbol digunakan untuk mewakili bilangan yang tidak diketahui. Berikut adalah contoh soal aljabar dan jawabannya:

1. Selesaikan persamaan berikut: 2x + 5 = 11
2. Tentukan nilai x yang memenuhi persamaan berikut: x² – 4x + 3 = 0

Selesaikan persamaan berikut: 2x + 5 = 11

Untuk menyelesaikan persamaan tersebut, kita perlu mengisolasi x di satu sisi persamaan. Berikut langkah-langkahnya:

1. Kurangi 5 dari kedua sisi persamaan:
2. 2x + 5 – 5 = 11 – 5
3. 2x = 6
4. Bagi kedua sisi persamaan dengan 2:
5. 2x/2 = 6/2
6. x = 3

Jadi, nilai x yang memenuhi persamaan 2x + 5 = 11 adalah x = 3.

Tentukan nilai x yang memenuhi persamaan berikut: x² – 4x + 3 = 0

Persamaan ini merupakan persamaan kuadrat, yang dapat diselesaikan dengan menggunakan rumus kuadrat. Berikut rumus kuadrat:

x = (-b ± √(b² – 4ac)) / 2a

Dimana a, b, dan c adalah koefisien dari persamaan kuadrat ax² + bx + c = 0. Dalam persamaan x² – 4x + 3 = 0, a = 1, b = -4, dan c = 3. Substitusikan nilai-nilai tersebut ke dalam rumus kuadrat:

1. x = (4 ± √((-4)² – 4 * 1 * 3)) / (2 * 1)
2. x = (4 ± √(16 – 12)) / 2
3. x = (4 ± √4) / 2
4. x = (4 ± 2) / 2
5. x = 3 atau x = 1

Jadi, nilai x yang memenuhi persamaan x² – 4x + 3 = 0 adalah x = 3 atau x = 1.

Geometri

Geometri adalah cabang matematika yang mempelajari tentang bentuk, ukuran, posisi, dan sifat ruang. Berikut adalah contoh soal geometri dan jawabannya:

1. Hitunglah luas segitiga dengan alas 10 cm dan tinggi 8 cm.
2. Tentukan keliling lingkaran dengan diameter 14 cm.

Hitunglah luas segitiga dengan alas 10 cm dan tinggi 8 cm.

Rumus luas segitiga adalah:

Luas = (1/2) * alas * tinggi

Substitusikan nilai alas dan tinggi ke dalam rumus:

1. Luas = (1/2) * 10 cm * 8 cm
2. Luas = 40 cm²

Jadi, luas segitiga tersebut adalah 40 cm².

Tentukan keliling lingkaran dengan diameter 14 cm.

Rumus keliling lingkaran adalah:

Keliling = π * diameter

Dimana π (pi) adalah konstanta matematika yang nilainya sekitar 3.14. Substitusikan nilai diameter ke dalam rumus:

1. Keliling = 3.14 * 14 cm
2. Keliling = 43.96 cm

Jadi, keliling lingkaran tersebut adalah 43.96 cm.

Kalkulus

Kalkulus adalah cabang matematika yang mempelajari tentang perubahan. Kalkulus memiliki dua cabang utama, yaitu kalkulus diferensial dan kalkulus integral. Kalkulus diferensial mempelajari tentang laju perubahan, sedangkan kalkulus integral mempelajari tentang penjumlahan. Berikut adalah contoh soal kalkulus dan jawabannya:

1. Tentukan turunan dari fungsi f(x) = x² + 2x + 1.
2. Hitunglah integral dari fungsi f(x) = 2x + 1.

Tentukan turunan dari fungsi f(x) = x² + 2x + 1.

Turunan dari fungsi f(x) = x² + 2x + 1 adalah f'(x) = 2x + 2. Berikut langkah-langkahnya:

1. Turunan dari x² adalah 2x.
2. Turunan dari 2x adalah 2.
3. Turunan dari 1 adalah 0.

Jadi, turunan dari fungsi f(x) = x² + 2x + 1 adalah f'(x) = 2x + 2.

Hitunglah integral dari fungsi f(x) = 2x + 1.

Integral dari fungsi f(x) = 2x + 1 adalah F(x) = x² + x + C. Berikut langkah-langkahnya:

1. Integral dari 2x adalah x².
2. Integral dari 1 adalah x.
3. C adalah konstanta integrasi.

Jadi, integral dari fungsi f(x) = 2x + 1 adalah F(x) = x² + x + C.

Statistika

Statistika adalah cabang matematika yang mempelajari tentang pengumpulan, analisis, interpretasi, presentasi, dan organisasi data. Berikut adalah contoh soal statistika dan jawabannya:

1. Hitunglah rata-rata, median, dan modus dari data berikut: 2, 4, 5, 6, 6, 7, 8.
2. Tentukan varians dan standar deviasi dari data berikut: 2, 4, 5, 6, 6, 7, 8.

Hitunglah rata-rata, median, dan modus dari data berikut: 2, 4, 5, 6, 6, 7, 8.

Berikut langkah-langkah menghitung rata-rata, median, dan modus:

1. Rata-rata: Jumlahkan semua data dan bagi dengan jumlah data.
2. Median: Urutkan data dari yang terkecil hingga terbesar. Median adalah data yang berada di tengah. Jika jumlah data genap, median adalah rata-rata dari dua data tengah.
3. Modus: Data yang paling sering muncul.

Berikut perhitungannya:

1. Rata-rata = (2 + 4 + 5 + 6 + 6 + 7 + 8) / 7 = 5.43
2. Median = 6
3. Modus = 6

Jadi, rata-rata data tersebut adalah 5.43, mediannya adalah 6, dan modusnya adalah 6.

Tentukan varians dan standar deviasi dari data berikut: 2, 4, 5, 6, 6, 7, 8.

Varians adalah ukuran sebaran data terhadap rata-rata. Standar deviasi adalah akar kuadrat dari varians. Berikut langkah-langkah menghitung varians dan standar deviasi:

1. Hitung rata-rata data.
2. Hitung selisih setiap data dengan rata-rata.
3. Kuadratkan setiap selisih.
4. Jumlahkan semua kuadrat selisih.
5. Bagi jumlah kuadrat selisih dengan jumlah data dikurangi 1.
6. Akar kuadratkan hasil langkah 5 untuk mendapatkan standar deviasi.

Berikut perhitungannya:

1. Rata-rata = 5.43
2. Selisih data dengan rata-rata: -3.43, -1.43, -0.43, 0.57, 0.57, 1.57, 2.57
3. Kuadrat selisih: 11.76, 2.04, 0.18, 0.33, 0.33, 2.46, 6.60
4. Jumlah kuadrat selisih = 23.69
5. Varians = 23.69 / (7 – 1) = 3.95
6. Standar deviasi = √3.95 = 1.99

Jadi, varians data tersebut adalah 3.95 dan standar deviasinya adalah 1.99.

Tingkat Kesulitan Soal

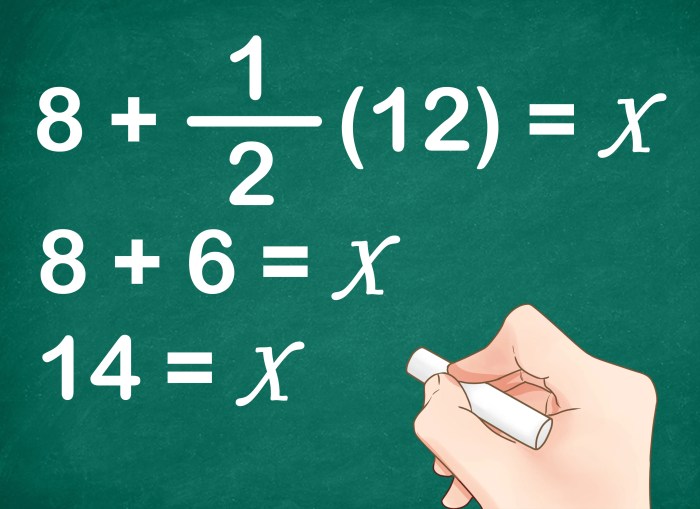
Tingkat kesulitan soal matematika dapat bervariasi, tergantung pada jenjang pendidikan. Soal matematika tingkat SD cenderung lebih sederhana dibandingkan dengan soal matematika tingkat SMA atau perguruan tinggi. Soal-soal ini dirancang untuk menguji pemahaman dasar tentang konsep matematika dan kemampuan siswa dalam menyelesaikan masalah sederhana. Berikut adalah contoh soal matematika dari berbagai tingkat pendidikan:

Soal Matematika Tingkat SD

Soal matematika tingkat SD biasanya berfokus pada konsep dasar seperti penjumlahan, pengurangan, perkalian, pembagian, geometri sederhana, dan pengukuran.

• Contoh soal: Andi memiliki 5 buah apel, kemudian dia diberi 3 buah apel lagi. Berapa total apel yang dimiliki Andi sekarang?
• Jawaban: 5 + 3 = 8. Jadi, Andi memiliki 8 buah apel.

Soal Matematika Tingkat SMP

Soal matematika tingkat SMP mulai memperkenalkan konsep-konsep yang lebih kompleks, seperti aljabar, persamaan linear, geometri, dan trigonometri.

• Contoh soal: Tentukan nilai x yang memenuhi persamaan 2x + 5 = 11.
• Jawaban: 2x = 11 – 5. 2x = 6. x = 6/2. x = 3.

Soal Matematika Tingkat SMA

Soal matematika tingkat SMA mencakup topik-topik yang lebih lanjut, seperti kalkulus, statistika, dan peluang.

• Contoh soal: Tentukan turunan pertama dari fungsi f(x) = x^2 + 3x – 2.
• Jawaban: f'(x) = 2x + 3.

Soal Matematika Tingkat Perguruan Tinggi

Soal matematika tingkat perguruan tinggi biasanya melibatkan konsep-konsep yang lebih abstrak dan kompleks, seperti aljabar linear, kalkulus multivariabel, dan topologi.

• Contoh soal: Tentukan nilai eigen dari matriks A = [[2, 1], [1, 2]].
• Jawaban: Untuk mencari nilai eigen, kita perlu menyelesaikan persamaan det(A – λI) = 0, di mana λ adalah nilai eigen dan I adalah matriks identitas. Dalam kasus ini, kita mendapatkan persamaan (2 – λ)^2 – 1 = 0. Menyelesaikan persamaan ini, kita mendapatkan nilai eigen λ = 1 dan λ = 3.

Format Soal Matematika

Soal matematika dapat disusun dalam berbagai format, disesuaikan dengan tujuan dan tingkat kesulitan yang ingin dicapai. Format soal yang umum digunakan antara lain pilihan ganda, essay, uraian, dan isian singkat. Masing-masing format memiliki karakteristik dan keunggulannya sendiri.

Soal Pilihan Ganda

Soal pilihan ganda merupakan format soal yang paling umum digunakan dalam penilaian matematika. Format ini terdiri dari pertanyaan atau pernyataan yang diikuti oleh beberapa pilihan jawaban, di mana hanya satu jawaban yang benar. Soal pilihan ganda dinilai lebih mudah dan cepat dalam proses penilaian, namun format ini juga memiliki kekurangan, yaitu memungkinkan siswa untuk menebak jawaban.

• Contoh soal:

Hasil dari 2³ + 3² adalah …

1. 11
2. 17
3. 23
4. 29

• Jawaban: (B) 17

Pembahasan:

2³ + 3² = 8 + 9 = 17

Soal Essay

Soal essay merupakan format soal yang mengharuskan siswa untuk menuliskan jawaban secara lengkap dan terstruktur. Format ini dinilai lebih efektif dalam mengukur kemampuan berpikir kritis, kemampuan menganalisis, dan kemampuan menyusun argumentasi. Soal essay biasanya membutuhkan waktu yang lebih lama untuk dikerjakan dan dinilai.

• Contoh soal:

Jelaskan bagaimana cara menyelesaikan persamaan linear satu variabel dengan metode eliminasi!

• Jawaban:

Metode eliminasi merupakan salah satu metode untuk menyelesaikan persamaan linear satu variabel. Metode ini dilakukan dengan cara menghilangkan salah satu variabel dari kedua persamaan dengan cara menjumlahkan atau mengurangkan kedua persamaan tersebut. Berikut langkah-langkah menyelesaikan persamaan linear satu variabel dengan metode eliminasi:

1. Selesaikan persamaan linear satu variabel dengan cara menghilangkan salah satu variabel dari kedua persamaan dengan cara menjumlahkan atau mengurangkan kedua persamaan tersebut. Berikut langkah-langkah menyelesaikan persamaan linear satu variabel dengan metode eliminasi:
2. Tentukan variabel yang akan dihilangkan.
3. Kalikan kedua persamaan dengan konstanta tertentu agar koefisien variabel yang akan dihilangkan sama besar.
4. Jumlahkan atau kurangkan kedua persamaan tersebut.
5. Selesaikan persamaan yang dihasilkan untuk mendapatkan nilai variabel yang tidak dihilangkan.
6. Substitusikan nilai variabel yang telah diperoleh ke salah satu persamaan awal untuk mendapatkan nilai variabel yang dihilangkan.

Contoh:

Selesaikan sistem persamaan linear berikut dengan metode eliminasi!

2x + 3y = 11

x – 2y = -5

Penyelesaian:

Langkah 1: Tentukan variabel yang akan dihilangkan. Dalam contoh ini, kita akan menghilangkan variabel x.

Langkah 2: Kalikan kedua persamaan dengan konstanta tertentu agar koefisien variabel x sama besar. Kalikan persamaan kedua dengan 2, sehingga diperoleh:

2x + 3y = 11

2x – 4y = -10

Langkah 3: Kurangkan kedua persamaan tersebut, sehingga diperoleh:

7y = 21

Langkah 4: Selesaikan persamaan yang dihasilkan untuk mendapatkan nilai y. y = 21/7 = 3.

Langkah 5: Substitusikan nilai y = 3 ke salah satu persamaan awal untuk mendapatkan nilai x. Misalkan kita substitusikan ke persamaan pertama:

2x + 3(3) = 11

Nggak cuma matematika, fisika juga punya banyak contoh soal dan jawabannya, lho! Buat kamu yang lagi belajar tentang gelombang cahaya di kelas 11, bisa nih cobain beberapa soal latihan di contoh soal dan pembahasan gelombang cahaya fisika kelas 11.

Soal-soal ini bisa bantu kamu memahami konsep dasar gelombang cahaya dan melatih kemampuan analisis kamu. Nah, setelah latihan soal fisika, kamu bisa kembali ke soal-soal matematika untuk mengasah logika dan kemampuan berpikir matematismu.

2x + 9 = 11

2x = 2

x = 1

Jadi, solusi dari sistem persamaan linear tersebut adalah x = 1 dan y = 3.

Soal Uraian

Soal uraian merupakan format soal yang mengharuskan siswa untuk menuliskan jawaban secara lengkap dan detail. Format ini dinilai lebih efektif dalam mengukur kemampuan berpikir kritis, kemampuan menganalisis, dan kemampuan menyusun argumentasi. Soal uraian biasanya membutuhkan waktu yang lebih lama untuk dikerjakan dan dinilai.

• Contoh soal:

Jelaskan perbedaan antara segitiga siku-siku, segitiga sama kaki, dan segitiga sama sisi!

• Jawaban:

Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Berikut perbedaan antara segitiga siku-siku, segitiga sama kaki, dan segitiga sama sisi:

1. Segitiga siku-siku adalah segitiga yang memiliki satu sudut siku-siku (90 derajat). Sisi di hadapan sudut siku-siku disebut hipotenusa, sedangkan dua sisi lainnya disebut kaki.
2. Segitiga sama kaki adalah segitiga yang memiliki dua sisi yang sama panjang. Kedua sudut yang berhadapan dengan sisi yang sama panjang juga sama besar.
3. Segitiga sama sisi adalah segitiga yang memiliki ketiga sisi yang sama panjang. Ketiga sudutnya juga sama besar, yaitu 60 derajat.

Soal Isian Singkat

Soal isian singkat merupakan format soal yang mengharuskan siswa untuk mengisi jawaban yang singkat dan tepat. Format ini dinilai lebih efektif dalam mengukur pemahaman konsep dan kemampuan mengingat. Soal isian singkat biasanya lebih mudah dan cepat untuk dikerjakan dan dinilai.

• Contoh soal:

Tuliskan rumus luas lingkaran!

• Jawaban:

L = πr²

Keterangan:

L = luas lingkaran

π = 3,14

r = jari-jari lingkaran

Contoh Soal dengan Gambar

Soal matematika yang menggunakan gambar dapat membantu siswa dalam memahami konsep matematika dengan lebih mudah. Gambar dapat memberikan representasi visual dari konsep abstrak, sehingga siswa dapat lebih mudah membayangkan dan menyelesaikan masalah.

Contoh Soal

Berikut adalah contoh soal matematika yang menggunakan gambar:

Soal: Hitunglah luas persegi panjang pada gambar di atas.

Jawaban:
Luas persegi panjang = panjang x lebar
Luas persegi panjang = 10 cm x 5 cm
Luas persegi panjang = 50 cm²

Langkah-langkah Penyelesaian Soal Matematika yang Menggunakan Gambar

Berikut adalah langkah-langkah penyelesaian soal matematika yang menggunakan gambar:

1. Pahami gambar: Perhatikan gambar dengan seksama dan identifikasi informasi yang diberikan dalam gambar.
2. Tentukan konsep matematika yang terkait: Tentukan konsep matematika apa yang terkait dengan gambar tersebut, misalnya luas, keliling, volume, sudut, dan lain-lain.
3. Terapkan rumus: Gunakan rumus matematika yang sesuai untuk menyelesaikan soal.
4. Hitung jawaban: Hitung jawaban dengan menggunakan informasi yang diberikan dalam gambar dan rumus yang telah dipilih.

Hubungan antara Jenis Soal Matematika dan Jenis Gambar yang Digunakan

Berikut adalah tabel yang menunjukkan hubungan antara jenis soal matematika dan jenis gambar yang digunakan:

Jenis Soal Matematika	Jenis Gambar
Luas	Persegi, persegi panjang, lingkaran, segitiga
Keliling	Persegi, persegi panjang, lingkaran, segitiga
Volume	Kubus, balok, tabung, kerucut, bola
Sudut	Sudut lancip, sudut tumpul, sudut siku-siku
Persentase	Diagram lingkaran, diagram batang, diagram garis

Contoh Soal dengan Konteks Nyata

Mempelajari matematika tidak hanya sebatas menghafal rumus dan menyelesaikan soal-soal abstrak. Matematika hadir dalam kehidupan sehari-hari dan membantu kita memahami berbagai fenomena yang terjadi di sekitar kita. Dengan menghubungkan konsep matematika dengan konteks nyata, pembelajaran menjadi lebih menarik dan bermakna. Berikut beberapa contoh soal matematika yang dikaitkan dengan kehidupan sehari-hari, masalah sosial, dan ekonomi.

Contoh Soal dalam Kehidupan Sehari-hari

Matematika seringkali digunakan dalam kegiatan sehari-hari, seperti menghitung kebutuhan bahan makanan, menentukan jarak tempuh, atau menghitung biaya perjalanan. Berikut contohnya:

• Ibu membutuhkan 2 kg gula untuk membuat kue. Jika harga gula Rp15.000 per kg, berapa total biaya yang harus dibayarkan Ibu?
• Andi bersepeda ke rumah nenek dengan kecepatan 15 km/jam. Jarak rumah Andi ke rumah nenek 10 km. Berapa lama waktu yang dibutuhkan Andi untuk sampai ke rumah nenek?

Contoh Soal dalam Masalah Sosial

Matematika juga dapat digunakan untuk menganalisis masalah sosial, seperti distribusi penduduk, tingkat kemiskinan, atau angka kriminalitas. Berikut contohnya:

• Sebuah desa memiliki penduduk 1.000 jiwa. Jika 20% penduduknya miskin, berapa jumlah penduduk miskin di desa tersebut?
• Berdasarkan data, angka kriminalitas di suatu kota meningkat 10% setiap tahun. Jika tahun ini angka kriminalitas mencapai 500 kasus, berapa perkiraan angka kriminalitas tahun depan?

Contoh Soal dalam Masalah Ekonomi

Dalam dunia ekonomi, matematika digunakan untuk menganalisis data pasar, menghitung keuntungan, dan mengelola keuangan. Berikut contohnya:

• Sebuah toko menjual baju dengan harga Rp100.000 per potong. Jika toko tersebut mendapatkan keuntungan 20% dari setiap penjualan, berapa harga beli baju tersebut?
• Seorang pengusaha menabung Rp10.000.000 di bank dengan bunga 5% per tahun. Berapa total uang yang dimiliki pengusaha tersebut setelah 2 tahun?

Contoh Soal dengan Aplikasi: Contoh Soal Matematika Dan Jawabannya

Matematika tidak hanya hadir di bangku sekolah, tetapi juga memiliki peran penting dalam kehidupan sehari-hari. Matematika menjadi dasar dari berbagai bidang, termasuk teknologi, kesehatan, dan lingkungan. Dalam contoh-contoh soal berikut, kita akan melihat bagaimana matematika diterapkan dalam bidang-bidang tersebut.

Teknologi, Contoh soal matematika dan jawabannya

Matematika berperan penting dalam pengembangan teknologi, khususnya dalam bidang komputasi, pemrograman, dan desain.

• Sebuah perusahaan teknologi sedang mengembangkan algoritma baru untuk memprediksi cuaca. Algoritma tersebut menggunakan data historis suhu, kelembaban, dan kecepatan angin selama 10 tahun terakhir. Jika data tersebut diwakili oleh matriks A dengan dimensi 3650 x 10 (365 hari x 10 tahun), berapa banyak elemen yang terdapat dalam matriks A?

Jawaban: Jumlah elemen dalam matriks A adalah 3650 x 10 = 36.500 elemen.

Kesehatan

Matematika memiliki peran vital dalam bidang kesehatan, khususnya dalam analisis data medis, pengembangan obat, dan pemodelan penyakit.

• Sebuah rumah sakit ingin mengetahui rata-rata lama rawat inap pasien dengan penyakit jantung. Data yang diperoleh dari 100 pasien menunjukkan bahwa lama rawat inap mereka berkisar antara 3 hingga 10 hari. Jika rata-rata lama rawat inap adalah 6 hari, bagaimana cara menghitung standar deviasi dari data tersebut?

Jawaban: Standar deviasi dapat dihitung dengan menggunakan rumus standar deviasi populasi atau sampel, tergantung pada apakah data yang diperoleh mewakili seluruh populasi pasien dengan penyakit jantung atau hanya sampel dari populasi tersebut.

Lingkungan

Matematika digunakan untuk menganalisis data lingkungan, memodelkan perubahan iklim, dan merancang solusi untuk masalah lingkungan.

• Sebuah perusahaan ingin membangun pembangkit listrik tenaga surya. Mereka ingin menghitung luas lahan yang dibutuhkan untuk menghasilkan energi listrik sebesar 100 kilowatt. Jika efisiensi panel surya adalah 15% dan intensitas sinar matahari rata-rata adalah 1 kilowatt per meter persegi, berapa luas lahan yang dibutuhkan?

Jawaban: Luas lahan yang dibutuhkan dapat dihitung dengan rumus: Luas = Daya / (Efisiensi x Intensitas). Dalam kasus ini, Luas = 100 kilowatt / (0,15 x 1 kilowatt per meter persegi) = 666,67 meter persegi.

Contoh Soal dengan Rumus

Contoh soal matematika yang menggunakan rumus tertentu dapat membantu kita memahami penerapan rumus tersebut dalam situasi nyata. Selain itu, melalui contoh soal, kita bisa melatih kemampuan menyelesaikan masalah matematika dengan lebih efektif.

Rumus Luas Persegi Panjang

Luas persegi panjang dihitung dengan rumus:

Luas = panjang x lebar

Sebagai contoh, kita akan menghitung luas sebuah persegi panjang dengan panjang 10 cm dan lebar 5 cm.

Diketahui:

• Panjang = 10 cm
• Lebar = 5 cm

Maka, luas persegi panjang tersebut adalah:

Luas = 10 cm x 5 cm = 50 cm²

Jadi, luas persegi panjang tersebut adalah 50 cm².

Rumus Keliling Lingkaran

Keliling lingkaran dihitung dengan rumus:

Keliling = 2 x π x jari-jari

Dimana π (pi) adalah konstanta dengan nilai sekitar 3.14.

Sebagai contoh, kita akan menghitung keliling sebuah lingkaran dengan jari-jari 7 cm.

Diketahui:

• Jari-jari = 7 cm

Maka, keliling lingkaran tersebut adalah:

Keliling = 2 x 3.14 x 7 cm = 43.96 cm

Jadi, keliling lingkaran tersebut adalah 43.96 cm.

Hubungan Jenis Soal Matematika dan Rumus

Berikut adalah tabel yang menunjukkan hubungan antara jenis soal matematika dan rumus yang digunakan:

Jenis Soal	Rumus
Luas Persegi Panjang	Luas = panjang x lebar
Keliling Persegi Panjang	Keliling = 2 x (panjang + lebar)
Luas Segitiga	Luas = 1/2 x alas x tinggi
Keliling Segitiga	Keliling = sisi 1 + sisi 2 + sisi 3
Luas Lingkaran	Luas = π x jari-jari2
Keliling Lingkaran	Keliling = 2 x π x jari-jari

Contoh Soal dengan Strategi Penyelesaian

Dalam memecahkan soal matematika, terkadang kita dihadapkan pada beragam cara penyelesaian yang bisa diterapkan. Memahami berbagai strategi ini dapat membantu kita memilih pendekatan yang paling efisien dan mudah dipahami untuk menyelesaikan masalah tertentu. Artikel ini akan membahas contoh soal matematika yang dapat diselesaikan dengan berbagai strategi, serta langkah-langkah penyelesaiannya.

Contoh Soal dan Strategi Penyelesaian

Misalnya, perhatikan soal berikut:

Sebuah toko menjual 2 jenis baju. Baju jenis A dijual dengan harga Rp. 100.000,- per potong, sedangkan baju jenis B dijual dengan harga Rp. 150.000,- per potong. Jika toko tersebut menjual 50 potong baju dan memperoleh total pendapatan Rp. 6.000.000,- , berapa banyak baju jenis A dan jenis B yang terjual?

Soal ini dapat diselesaikan dengan beberapa strategi, seperti:

• Strategi Aljabar

Misalkan x adalah jumlah baju jenis A yang terjual dan y adalah jumlah baju jenis B yang terjual. Maka, kita dapat membuat sistem persamaan linear:

x + y = 50
100.000x + 150.000y = 6.000.000

Selanjutnya, kita dapat menyelesaikan sistem persamaan ini dengan metode substitusi atau eliminasi. Misalnya, dengan metode substitusi, kita dapat menyelesaikan persamaan pertama untuk x: x = 50 – y. Kemudian, kita substitusikan nilai x ke dalam persamaan kedua, sehingga diperoleh:

100.000(50 – y) + 150.000y = 6.000.000

Selesaikan persamaan tersebut untuk mendapatkan nilai y. Setelah mendapatkan nilai y, substitusikan kembali ke persamaan pertama untuk mendapatkan nilai x.

• Strategi Persamaan Linear

Strategi ini mirip dengan strategi aljabar, namun lebih fokus pada manipulasi persamaan linear untuk menemukan solusi. Misalnya, kita dapat mengubah persamaan kedua menjadi:

2x + 3y = 120

Kemudian, kita dapat menyelesaikan persamaan ini bersamaan dengan persamaan pertama (x + y = 50) dengan metode eliminasi atau substitusi.

• Strategi Menebak dan Memeriksa

Strategi ini melibatkan menebak nilai x dan y yang memenuhi persamaan. Kita dapat mulai dengan menebak nilai x dan y yang relatif mudah, seperti x = 20 dan y = 30. Kemudian, kita periksa apakah nilai tersebut memenuhi persamaan. Jika tidak, kita dapat mengubah nilai x dan y dan mengulangi proses ini hingga menemukan solusi yang tepat.

Hubungan Jenis Soal dan Strategi Penyelesaian

Jenis Soal	Strategi Penyelesaian
Soal yang melibatkan persamaan linear	Strategi Aljabar, Strategi Persamaan Linear
Soal yang melibatkan persentase atau proporsi	Strategi Perbandingan, Strategi Persentase
Soal yang melibatkan pola atau urutan	Strategi Menemukan Pola, Strategi Induksi Matematika
Soal yang melibatkan geometri	Strategi Geometri, Strategi Trigonometri

Contoh Soal dengan Penjelasan Lengkap

Salah satu cara terbaik untuk memahami konsep matematika adalah dengan mengerjakan soal latihan. Artikel ini akan memberikan contoh soal matematika yang disertai dengan penjelasan langkah-langkah penyelesaian secara detail, disertai jawabannya. Selain itu, kita akan membahas konsep matematika yang dipelajari dalam contoh soal tersebut.

Persamaan Linear Satu Variabel

Persamaan linear satu variabel merupakan persamaan yang hanya memiliki satu variabel dengan pangkat tertinggi 1. Bentuk umum persamaan linear satu variabel adalah ax + b = c, dengan a, b, dan c adalah konstanta dan a ≠ 0.

Untuk menyelesaikan persamaan linear satu variabel, kita perlu mencari nilai variabel yang memenuhi persamaan tersebut. Ada beberapa cara untuk menyelesaikan persamaan linear satu variabel, seperti:

• Metode eliminasi
• Metode substitusi
• Metode grafik

Berikut adalah contoh soal persamaan linear satu variabel:

Contoh Soal

Tentukan nilai x yang memenuhi persamaan 2x + 5 = 11.

Langkah-langkah Penyelesaian

1. Kurangi kedua ruas persamaan dengan 5:
2. 2x + 5 – 5 = 11 – 5
3. 2x = 6
4. Bagi kedua ruas persamaan dengan 2:
5. 2x / 2 = 6 / 2
6. x = 3

Jawaban

Nilai x yang memenuhi persamaan 2x + 5 = 11 adalah x = 3.

Dalam menyelesaikan persamaan linear satu variabel, kita harus melakukan operasi matematika yang sama pada kedua ruas persamaan agar persamaan tetap berlaku.

Penutupan

Melalui contoh soal matematika dan jawabannya yang beragam ini, Anda telah menjelajahi berbagai aspek penting dalam matematika. Dari aljabar hingga kalkulus, dari soal dasar hingga soal tingkat lanjut, Anda telah mendapatkan pemahaman yang lebih luas tentang dunia angka. Ingat, kunci untuk menguasai matematika adalah latihan dan ketekunan. Jadi, teruslah berlatih, jangan takut untuk mencoba, dan nikmati perjalanan menaklukkan dunia angka!

Sebarkan ini:

Posting terkait:

• Contoh Soal Bahasa Indonesia Kelas 3 SD Tema 1: Asyik Belajar Bahasa!

• Contoh Laporan Sementara Praktikum: Panduan Lengkap untuk Mahasiswa

• Contoh Soal Bahasa Indonesia Kelas 2 SD Semester 2: Uji Kemampuan Berbahasa Si Kecil