Contoh Soal Matematika Diskrit dan Penyelesaiannya: Memahami Konsep dan Penerapannya

Matematika diskrit, sebuah cabang matematika yang mempelajari objek-objek diskrit, seperti bilangan bulat, himpunan, dan graf, memiliki peran penting dalam berbagai bidang, termasuk komputer, ekonomi, dan statistika. Contoh Soal Matematika Diskrit dan Penyelesaiannya akan menjadi panduan yang menarik untuk memahami konsep-konsep dasar dan bagaimana matematika diskrit diterapkan dalam kehidupan nyata.

Melalui contoh-contoh soal yang disertai penyelesaian langkah demi langkah, Anda akan diajak menjelajahi dunia matematika diskrit, mulai dari logika proposisional hingga algoritma pengurutan. Anda akan menemukan bagaimana konsep-konsep ini saling terkait dan bagaimana mereka dapat digunakan untuk memecahkan masalah-masalah yang kompleks.

Pengertian Matematika Diskrit

Matematika diskrit adalah cabang matematika yang mempelajari objek-objek diskrit, yaitu objek yang dapat dihitung atau dipisahkan. Objek-objek diskrit ini dapat berupa bilangan bulat, titik-titik pada suatu grafik, atau elemen-elemen dalam suatu himpunan. Matematika diskrit berbeda dengan matematika kontinu yang mempelajari objek-objek yang dapat dibagi secara tak terhingga, seperti bilangan real atau fungsi kontinu.

Contoh Matematika Diskrit dalam Kehidupan Sehari-hari

Matematika diskrit memiliki banyak aplikasi dalam kehidupan sehari-hari, beberapa contohnya:

• Komputer: Matematika diskrit merupakan dasar dari ilmu komputer, terutama dalam pemrograman, algoritma, struktur data, dan keamanan komputer. Contohnya, penggunaan algoritma sorting dalam mengurutkan data, algoritma searching dalam mencari data, dan algoritma enkripsi dalam mengamankan data.
• Jaringan: Matematika diskrit digunakan untuk menganalisis dan mendesain jaringan, seperti jaringan komputer, jaringan komunikasi, dan jaringan transportasi. Contohnya, penggunaan teori graf untuk memodelkan jaringan dan menemukan jalur terpendek atau aliran maksimum.
• Logika: Matematika diskrit digunakan dalam logika, terutama dalam pembuktian teorema dan penalaran deduktif. Contohnya, penggunaan logika proposisional dan logika predikat untuk membangun argumen yang valid.
• Kriptografi: Matematika diskrit digunakan dalam kriptografi untuk mengamankan komunikasi dan data. Contohnya, penggunaan teori bilangan untuk membangun sistem enkripsi dan algoritma hashing.
• Game: Matematika diskrit digunakan dalam pengembangan game untuk membuat level, menentukan aturan, dan menghasilkan gerakan AI. Contohnya, penggunaan teori probabilitas untuk menentukan peluang dalam permainan.

Konsep Dasar Matematika Diskrit

Matematika diskrit adalah cabang matematika yang mempelajari objek-objek diskrit, yaitu objek yang terhitung dan terpisah. Matematika diskrit memiliki banyak aplikasi di berbagai bidang, seperti ilmu komputer, teknik, ekonomi, dan ilmu sosial.

Konsep dasar matematika diskrit meliputi logika, himpunan, relasi dan fungsi, graf, kombinatorika, dan algoritma. Berikut penjelasan singkat tentang setiap konsep tersebut.

Logika, Contoh soal matematika diskrit dan penyelesaiannya

Logika adalah studi tentang penalaran dan argumen yang valid. Dalam matematika diskrit, logika digunakan untuk menyatakan proposisi dan inferensi, serta untuk membuktikan teorema. Proposisi adalah pernyataan yang dapat bernilai benar atau salah. Inferensi adalah proses menarik kesimpulan dari proposisi yang diketahui.

• Contoh proposisi: “2 + 2 = 4” (benar) dan “Bumi berbentuk persegi” (salah).
• Contoh inferensi: “Jika hari hujan, maka saya membawa payung. Hari ini hujan. Oleh karena itu, saya membawa payung.”

Himpunan

Himpunan adalah koleksi objek yang terdefinisi dengan baik. Objek dalam suatu himpunan disebut elemen. Himpunan dapat didefinisikan dengan cara mencantumkan elemennya atau dengan cara memberikan aturan yang menentukan elemennya.

• Contoh himpunan: Himpunan bilangan bulat …, -2, -1, 0, 1, 2, …, himpunan huruf vokal a, i, u, e, o, himpunan warna pelangi merah, jingga, kuning, hijau, biru, nila, ungu.

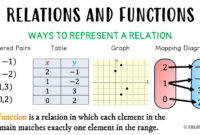
Relasi dan Fungsi

Relasi adalah hubungan antara elemen-elemen dari dua atau lebih himpunan. Fungsi adalah relasi khusus yang menghubungkan setiap elemen dalam satu himpunan (domain) dengan tepat satu elemen dalam himpunan lainnya (kodomain).

• Contoh relasi: Relasi “lebih besar dari” antara himpunan bilangan bulat. Misalnya, 5 lebih besar dari 3.
• Contoh fungsi: Fungsi kuadrat f(x) = x², yang menghubungkan setiap bilangan real x dengan kuadratnya.

Graf

Graf adalah struktur data yang terdiri dari simpul (vertex) dan sisi (edge). Simpul merepresentasikan objek, dan sisi merepresentasikan hubungan antara objek tersebut. Graf digunakan untuk memodelkan berbagai fenomena, seperti jaringan komputer, peta jalan, dan hubungan sosial.

• Contoh graf: Graf yang menggambarkan hubungan persahabatan antara beberapa orang. Simpul merepresentasikan orang, dan sisi merepresentasikan persahabatan.

Kombinatorika

Kombinatorika adalah studi tentang penataan, pemilihan, dan pengelompokan objek. Kombinatorika digunakan untuk menghitung jumlah kemungkinan cara untuk melakukan sesuatu, seperti memilih anggota tim atau menyusun kata sandi.

• Contoh kombinatorika: Menghitung jumlah cara untuk memilih 3 bola dari 5 bola yang berbeda.

Algoritma

Algoritma adalah sekumpulan instruksi yang terdefinisi dengan baik yang digunakan untuk menyelesaikan suatu masalah. Algoritma digunakan dalam berbagai bidang, seperti pemrograman komputer, ilmu komputer, dan matematika.

• Contoh algoritma: Algoritma penjumlahan dua bilangan bulat, algoritma pencarian data dalam suatu daftar, algoritma pengurutan data.

Contoh Soal Matematika Diskrit

Matematika diskrit merupakan cabang matematika yang mempelajari objek-objek diskrit, seperti bilangan bulat, himpunan, dan grafik. Matematika diskrit memiliki aplikasi yang luas di berbagai bidang, seperti ilmu komputer, teknik, dan ekonomi. Berikut adalah beberapa contoh soal matematika diskrit yang berkaitan dengan logika, himpunan, relasi, dan fungsi.

Logika, Contoh soal matematika diskrit dan penyelesaiannya

Logika merupakan cabang matematika yang mempelajari penalaran dan argumen yang valid. Logika digunakan untuk menguji kebenaran suatu pernyataan dan membangun sistem deduksi.

• Tentukan nilai kebenaran dari pernyataan berikut:
  • Jika hari ini hujan, maka saya akan membawa payung.
  • Hari ini hujan dan saya tidak membawa payung.

  Penyelesaian:

  Pernyataan pertama adalah implikasi. Implikasi hanya salah jika hipotesisnya benar dan konsekuensinya salah. Karena hari ini hujan dan saya tidak membawa payung, maka pernyataan pertama adalah salah. Pernyataan kedua adalah konjungsi. Konjungsi hanya benar jika kedua pernyataan yang dihubungkan oleh “dan” benar. Karena hari ini hujan dan saya tidak membawa payung, maka pernyataan kedua adalah benar.

  Contoh soal matematika diskrit dan penyelesaiannya bisa kamu temukan di berbagai sumber, mulai dari buku teks hingga website. Nah, buat kamu yang sedang mencari contoh soal tentang konsep dasar matematika diskrit, kamu bisa coba cek contoh soal c1 sampai c6 yang membahas tentang logika, himpunan, relasi, dan fungsi.

  Soal-soal tersebut bisa menjadi latihan yang bagus untuk menguji pemahaman kamu tentang konsep-konsep dasar matematika diskrit.

• Tentukan bentuk normal konjungtif (CNF) dari pernyataan berikut:

  Jika saya lulus ujian, maka saya akan pergi ke pesta.

  Penyelesaian:

  Misalkan p menyatakan “Saya lulus ujian” dan q menyatakan “Saya akan pergi ke pesta”. Pernyataan tersebut dapat ditulis dalam bentuk implikasi: p → q. Untuk mendapatkan bentuk normal konjungtif, kita dapat menggunakan hukum logika berikut:

  p → q ≡ ¬p ∨ q

  Dengan demikian, bentuk normal konjungtif dari pernyataan tersebut adalah ¬p ∨ q.

Himpunan

Himpunan adalah kumpulan objek yang berbeda. Himpunan dapat didefinisikan dengan menggunakan notasi pembentuk himpunan atau dengan mendaftar semua elemennya.

• Tentukan himpunan bagian dari himpunan 1, 2, 3.

  Penyelesaian:

  Himpunan bagian dari himpunan 1, 2, 3 adalah:

  • (himpunan kosong)
  • 1
  • 2
  • 3
  • 1, 2
  • 1, 3
  • 2, 3
  • 1, 2, 3
• Tentukan operasi himpunan berikut:
  • A ∪ B, jika A = 1, 2, 3 dan B = 2, 3, 4
  • A ∩ B, jika A = 1, 2, 3 dan B = 2, 3, 4
  • A – B, jika A = 1, 2, 3 dan B = 2, 3, 4

  Penyelesaian:

  A ∪ B adalah gabungan dari A dan B, yaitu himpunan yang berisi semua elemen A dan B. Jadi, A ∪ B = 1, 2, 3, 4.

  A ∩ B adalah irisan dari A dan B, yaitu himpunan yang berisi semua elemen yang terdapat di A dan B. Jadi, A ∩ B = 2, 3.

  A – B adalah selisih dari A dan B, yaitu himpunan yang berisi semua elemen A yang tidak terdapat di B. Jadi, A – B = 1.

Relasi dan Fungsi

Relasi adalah hubungan antara dua himpunan. Fungsi adalah relasi khusus yang memasangkan setiap elemen di domain dengan tepat satu elemen di kodomain.

• Tentukan apakah relasi R = (1, 2), (2, 3), (3, 1) pada himpunan 1, 2, 3 adalah relasi ekuivalen.

  Penyelesaian:

  Relasi ekuivalen harus memenuhi tiga sifat:

  • Reflektif: Untuk setiap elemen a di himpunan, (a, a) harus berada di R. Relasi R tidak reflektif karena (1, 1), (2, 2), dan (3, 3) tidak berada di R.
  • Simetris: Untuk setiap elemen a dan b di himpunan, jika (a, b) berada di R, maka (b, a) juga harus berada di R. Relasi R simetris karena jika (a, b) berada di R, maka (b, a) juga berada di R. Misalnya, (1, 2) berada di R dan (2, 1) juga berada di R.
  • Transitif: Untuk setiap elemen a, b, dan c di himpunan, jika (a, b) dan (b, c) berada di R, maka (a, c) juga harus berada di R. Relasi R tidak transitif karena (1, 2) dan (2, 3) berada di R, tetapi (1, 3) tidak berada di R.

  Karena relasi R tidak memenuhi semua sifat relasi ekuivalen, maka relasi R bukan relasi ekuivalen.

• Tentukan apakah fungsi f: R → R, f(x) = x^2 adalah fungsi surjektif.

  Penyelesaian:

  Fungsi surjektif adalah fungsi yang memetakan setiap elemen di kodomain dengan setidaknya satu elemen di domain. Fungsi f(x) = x^2 tidak surjektif karena tidak ada bilangan real x yang dapat dipetakan ke bilangan real negatif. Misalnya, tidak ada bilangan real x yang dapat dipetakan ke -1. Jadi, fungsi f(x) = x^2 bukan fungsi surjektif.

Penyelesaian Soal Matematika Diskrit

Matematika diskrit merupakan cabang matematika yang mempelajari objek-objek diskrit, seperti bilangan bulat, graf, dan himpunan. Soal-soal matematika diskrit seringkali melibatkan logika, kombinatorik, dan teori himpunan. Untuk menyelesaikan soal-soal tersebut, diperlukan pemahaman yang mendalam tentang konsep-konsep dasar matematika diskrit dan penguasaan metode penyelesaian yang tepat.

Langkah-Langkah Umum dalam Menyelesaikan Soal Matematika Diskrit

Secara umum, menyelesaikan soal matematika diskrit dapat dilakukan dengan mengikuti langkah-langkah berikut:

• Memahami Soal: Langkah pertama adalah memahami dengan baik apa yang ditanyakan dalam soal. Identifikasi informasi yang diberikan dan apa yang ingin dicari.
• Menentukan Konsep dan Metode: Setelah memahami soal, tentukan konsep matematika diskrit yang relevan dengan soal tersebut. Misalnya, jika soal berkaitan dengan kombinatorik, maka Anda perlu memahami konsep faktorial, kombinasi, dan permutasi.
• Menerapkan Metode: Setelah menentukan konsep dan metode yang tepat, terapkan metode tersebut untuk menyelesaikan soal. Pastikan langkah-langkah yang Anda ambil sesuai dengan metode yang dipilih.
• Memeriksa Jawaban: Setelah mendapatkan jawaban, periksa kembali jawaban tersebut untuk memastikan keakuratannya. Pastikan jawaban Anda masuk akal dan konsisten dengan informasi yang diberikan dalam soal.

Cara Mengidentifikasi Jenis Soal Matematika Diskrit dan Menentukan Metode Penyelesaian yang Tepat

Untuk menentukan jenis soal matematika diskrit dan metode penyelesaian yang tepat, perhatikan beberapa hal berikut:

• Jenis Objek: Perhatikan jenis objek yang dibahas dalam soal. Apakah soal membahas tentang bilangan bulat, graf, himpunan, atau objek diskrit lainnya?
• Konsep yang Diharapkan: Perhatikan konsep matematika diskrit yang mungkin digunakan dalam soal. Misalnya, jika soal membahas tentang bilangan bulat, maka konsep yang mungkin digunakan adalah induksi matematika, rekursi, atau teori bilangan.
• Tujuan Soal: Perhatikan tujuan soal. Apakah soal ingin menghitung, membuktikan, atau mencari solusi untuk suatu masalah?

Contoh Ilustrasi Penyelesaian Soal Matematika Diskrit

Misalnya, kita ingin menyelesaikan soal berikut:

Buktikan bahwa jumlah n bilangan bulat ganjil pertama sama dengan n².

• Memahami Soal: Soal ini meminta kita untuk membuktikan suatu pernyataan matematika. Pernyataan tersebut menyatakan bahwa jumlah n bilangan bulat ganjil pertama sama dengan n².
• Menentukan Konsep dan Metode: Untuk membuktikan pernyataan ini, kita dapat menggunakan induksi matematika. Induksi matematika adalah metode pembuktian yang digunakan untuk membuktikan pernyataan yang berlaku untuk semua bilangan bulat positif.
• Menerapkan Metode:
  • Langkah dasar: Untuk n = 1, pernyataan tersebut benar karena jumlah 1 bilangan bulat ganjil pertama (yaitu 1) sama dengan 1².
  • Langkah induktif: Asumsikan bahwa pernyataan tersebut benar untuk n = k, yaitu jumlah k bilangan bulat ganjil pertama sama dengan k². Kita perlu menunjukkan bahwa pernyataan tersebut juga benar untuk n = k + 1.
  • Langkah induktif: Jumlah (k + 1) bilangan bulat ganjil pertama sama dengan jumlah k bilangan bulat ganjil pertama ditambah (2k + 1). Berdasarkan asumsi induktif, jumlah k bilangan bulat ganjil pertama sama dengan k², sehingga jumlah (k + 1) bilangan bulat ganjil pertama sama dengan k² + (2k + 1) = (k + 1)².
• Memeriksa Jawaban: Kita telah menunjukkan bahwa pernyataan tersebut benar untuk n = 1 dan bahwa jika pernyataan tersebut benar untuk n = k, maka pernyataan tersebut juga benar untuk n = k + 1. Oleh karena itu, berdasarkan prinsip induksi matematika, pernyataan tersebut benar untuk semua bilangan bulat positif n.

Aplikasi Matematika Diskrit

Matematika diskrit adalah cabang matematika yang mempelajari objek-objek diskrit, seperti bilangan bulat, graf, dan logika. Cabang ini memiliki aplikasi yang luas dalam berbagai bidang, termasuk komputer, ekonomi, statistika, dan riset operasi.

Aplikasi dalam Komputer

Matematika diskrit memiliki peran penting dalam berbagai aspek dunia komputer. Beberapa contohnya adalah:

• Pemrograman: Konsep matematika diskrit seperti struktur data, algoritma, dan logika digunakan dalam pengembangan perangkat lunak. Contohnya, algoritma pencarian dan pengurutan, yang merupakan konsep dasar dalam pemrograman, berasal dari matematika diskrit.
• Keamanan Data: Kriptografi, yang berkaitan dengan keamanan data, bergantung pada konsep matematika diskrit seperti teori bilangan dan aljabar abstrak. Misalnya, algoritma enkripsi modern seperti RSA menggunakan bilangan prima dan teori modular untuk mengamankan data.
• Algoritma Pencarian: Algoritma pencarian seperti algoritma pencarian terurut (binary search) dan algoritma pencarian terarah (breadth-first search) adalah contoh aplikasi matematika diskrit dalam pengembangan sistem pencarian yang efisien.

Aplikasi dalam Ekonomi

Matematika diskrit membantu dalam memahami dan memodelkan fenomena ekonomi. Berikut contohnya:

• Teori Permainan: Matematika diskrit digunakan untuk menganalisis strategi optimal dalam situasi di mana beberapa pemain terlibat. Contohnya, dalam teori lelang, matematika diskrit membantu memahami strategi penawaran optimal untuk memaksimalkan keuntungan.
• Teori Pilihan: Matematika diskrit membantu dalam memahami bagaimana individu membuat pilihan dalam kondisi terbatas. Contohnya, model matematika diskrit dapat digunakan untuk menganalisis bagaimana konsumen memilih barang dan jasa dengan anggaran terbatas.
• Ekonometri: Matematika diskrit digunakan dalam pengembangan model ekonometri untuk menganalisis data ekonomi. Contohnya, model regresi linier, yang merupakan alat penting dalam ekonometri, menggunakan konsep matematika diskrit untuk memperkirakan hubungan antara variabel ekonomi.

Aplikasi dalam Statistika

Matematika diskrit memainkan peran penting dalam berbagai aspek statistika. Contohnya:

• Probabilitas: Teori probabilitas, yang merupakan cabang matematika diskrit, merupakan dasar dari statistika. Konsep probabilitas digunakan untuk menganalisis dan memprediksi hasil dari kejadian acak.
• Statistika Inferensial: Matematika diskrit digunakan untuk mengembangkan metode inferensial statistik, seperti pengujian hipotesis dan interval kepercayaan. Metode ini memungkinkan kita untuk menarik kesimpulan tentang populasi berdasarkan sampel data.
• Statistika Deskriptif: Matematika diskrit digunakan dalam statistika deskriptif untuk meringkas dan menyajikan data. Contohnya, konsep kombinatorika digunakan untuk menghitung jumlah kemungkinan dalam sampel data.

Aplikasi dalam Riset Operasi

Matematika diskrit memiliki aplikasi yang luas dalam riset operasi, yang berkaitan dengan optimasi sistem dan pengambilan keputusan. Berikut contohnya:

• Optimasi: Matematika diskrit digunakan untuk mengembangkan algoritma optimasi, yang bertujuan untuk menemukan solusi terbaik untuk masalah yang diberikan. Contohnya, algoritma pemrograman linear digunakan untuk menyelesaikan masalah optimasi dalam berbagai bidang, seperti manajemen produksi dan logistik.
• Teori Antrian: Matematika diskrit digunakan untuk menganalisis dan memodelkan sistem antrian, seperti antrian di supermarket atau pusat panggilan. Model matematika diskrit membantu dalam meminimalkan waktu tunggu dan meningkatkan efisiensi sistem antrian.
• Teori Graf: Teori graf, yang merupakan cabang matematika diskrit, digunakan untuk memodelkan dan menganalisis jaringan. Contohnya, teori graf digunakan untuk memodelkan jaringan jalan, jaringan komputer, dan jaringan sosial.

Contoh Soal Logika

Logika merupakan cabang filsafat yang mempelajari penalaran yang valid. Logika membahas tentang cara berpikir secara benar dan sistematis, dengan fokus pada bentuk dan struktur argumen. Di dalam matematika diskrit, logika memiliki peran penting dalam membangun pernyataan, menguji kebenaran, dan menyusun bukti.

Logika terbagi menjadi beberapa jenis, di antaranya:

Logika Proposisional

Logika proposisional adalah sistem logika yang mempelajari proposisi dan hubungan antar proposisi. Proposisi adalah pernyataan yang bernilai benar atau salah. Hubungan antar proposisi dapat dibentuk dengan menggunakan konektor logika, seperti negasi, konjungsi, disjungsi, implikasi, dan biimplikasi.

Contoh soal logika proposisional:

Diketahui proposisi:

• p: “Hari ini hujan”
• q: “Saya membawa payung”

Buatlah tabel kebenaran untuk pernyataan “Jika hari ini hujan, maka saya membawa payung”.

Penyelesaian:

Pernyataan “Jika hari ini hujan, maka saya membawa payung” dapat ditulis dalam bentuk logika proposisional sebagai “p → q”. Tabel kebenaran untuk pernyataan ini adalah:

p	q	p → q
T	T	T
T	F	F
F	T	T
F	F	T

Dari tabel kebenaran, dapat disimpulkan bahwa pernyataan “Jika hari ini hujan, maka saya membawa payung” bernilai benar jika hari ini hujan dan saya membawa payung, atau jika hari ini tidak hujan. Pernyataan ini bernilai salah jika hari ini hujan tetapi saya tidak membawa payung.

Logika Predikat

Logika predikat adalah sistem logika yang mempelajari predikat, variabel, dan kuantor. Predikat adalah pernyataan yang mengandung variabel, seperti “x adalah bilangan genap”. Variabel adalah simbol yang mewakili objek, seperti “x”. Kuantor adalah simbol yang menunjukkan jumlah objek yang memenuhi predikat, seperti “semua” dan “ada”.

Contoh soal logika predikat:

Buktikan dengan metode deduksi bahwa “Jika semua bilangan bulat adalah genap, maka 3 adalah bilangan genap”.

Penyelesaian:

* Premis 1: Semua bilangan bulat adalah genap.
* Premis 2: 3 adalah bilangan bulat.
* Kesimpulan: 3 adalah bilangan genap.

Metode deduksi dapat digunakan untuk membuktikan kesimpulan dari premis-premis yang diberikan. Dalam contoh ini, kita dapat menggunakan modus ponens untuk membuktikan kesimpulan. Modus ponens adalah aturan inferensi yang menyatakan bahwa jika p → q dan p benar, maka q juga benar.

* Dari premis 1, kita dapat menyimpulkan bahwa “Jika x adalah bilangan bulat, maka x adalah bilangan genap”.
* Dari premis 2, kita tahu bahwa 3 adalah bilangan bulat.
* Dengan menggunakan modus ponens, kita dapat menyimpulkan bahwa 3 adalah bilangan genap.

Logika Modal

Logika modal adalah sistem logika yang mempelajari modalitas, seperti kemungkinan, kewajiban, dan keperluan. Modalitas adalah sifat dari suatu proposisi yang menunjukkan bagaimana proposisi tersebut berhubungan dengan kenyataan.

Contoh soal logika modal:

Diketahui proposisi:

• p: “Saya akan pergi ke kampus”

Tentukan kemungkinan dunia yang memenuhi pernyataan “Mungkin saya akan pergi ke kampus”.

Penyelesaian:

Pernyataan “Mungkin saya akan pergi ke kampus” dapat ditulis dalam bentuk logika modal sebagai “◊p”. ◊ adalah operator modal yang menunjukkan kemungkinan.

Kemungkinan dunia yang memenuhi pernyataan “◊p” adalah semua dunia di mana saya pergi ke kampus. Misalnya, dalam satu kemungkinan dunia, saya mungkin pergi ke kampus karena saya merasa sehat. Dalam kemungkinan dunia lainnya, saya mungkin tidak pergi ke kampus karena saya sakit.

Metode kemungkinan dunia dapat digunakan untuk menganalisis pernyataan modal dengan melihat semua kemungkinan dunia yang memenuhi pernyataan tersebut.

Contoh Soal Himpunan: Contoh Soal Matematika Diskrit Dan Penyelesaiannya

Himpunan merupakan konsep dasar dalam matematika diskrit yang membahas tentang kumpulan objek yang terdefinisi dengan baik. Objek-objek dalam himpunan disebut sebagai elemen. Dalam matematika diskrit, kita seringkali bekerja dengan operasi himpunan seperti gabungan, irisan, dan selisih. Selain itu, konsep himpunan kuasa dan diagram Venn juga penting untuk memahami hubungan antar himpunan.

Operasi Himpunan

Operasi himpunan memungkinkan kita untuk menggabungkan, memotong, atau mengurangi himpunan. Berikut adalah beberapa contoh soal operasi himpunan beserta penyelesaiannya:

• Gabungan: Gabungan dua himpunan adalah himpunan yang berisi semua elemen dari kedua himpunan tersebut. Misalnya, jika A = 1, 2, 3 dan B = 3, 4, 5, maka gabungan A dan B adalah A ∪ B = 1, 2, 3, 4, 5.
• Irisan: Irisan dua himpunan adalah himpunan yang berisi semua elemen yang terdapat di kedua himpunan tersebut. Misalnya, jika A = 1, 2, 3 dan B = 3, 4, 5, maka irisan A dan B adalah A ∩ B = 3.
• Selisih: Selisih dua himpunan adalah himpunan yang berisi semua elemen yang terdapat di himpunan pertama tetapi tidak terdapat di himpunan kedua. Misalnya, jika A = 1, 2, 3 dan B = 3, 4, 5, maka selisih A dan B adalah A – B = 1, 2.

Himpunan Kuasa

Himpunan kuasa dari suatu himpunan adalah himpunan yang berisi semua himpunan bagian dari himpunan tersebut, termasuk himpunan kosong. Misalnya, himpunan kuasa dari himpunan A = 1, 2 adalah P(A) = , 1, 2, 1, 2.

Contoh soal:

1. Tentukan himpunan kuasa dari himpunan B = a, b, c.

Penyelesaian:

Himpunan bagian dari B adalah: , a, b, c, a, b, a, c, b, c, a, b, c.
Maka, himpunan kuasa dari B adalah P(B) = , a, b, c, a, b, a, c, b, c, a, b, c.

Diagram Venn

Diagram Venn adalah diagram yang digunakan untuk menggambarkan hubungan antar himpunan. Diagram Venn menggunakan lingkaran untuk mewakili himpunan, dan daerah yang tumpang tindih menunjukkan irisan antar himpunan.

Contoh soal:

1. Misalkan A = 1, 2, 3, 4 dan B = 3, 4, 5, 6. Gambarlah diagram Venn untuk menunjukkan hubungan antar himpunan A dan B.

Penyelesaian:

Diagram Venn untuk A dan B akan memiliki dua lingkaran yang saling tumpang tindih. Lingkaran pertama mewakili himpunan A, dan lingkaran kedua mewakili himpunan B. Daerah yang tumpang tindih menunjukkan irisan A dan B, yaitu 3, 4.

Berikut adalah contoh ilustrasi diagram Venn untuk soal tersebut:

Gambarlah dua lingkaran yang saling tumpang tindih. Beri label A pada lingkaran pertama dan B pada lingkaran kedua. Di dalam lingkaran A, tuliskan elemen-elemennya, yaitu 1, 2, 3, dan 4. Di dalam lingkaran B, tuliskan elemen-elemennya, yaitu 3, 4, 5, dan 6. Di daerah tumpang tindih, tuliskan elemen-elemen yang terdapat di kedua himpunan, yaitu 3 dan 4.

Contoh Soal Graf

Graf merupakan salah satu konsep penting dalam matematika diskrit. Graf digunakan untuk merepresentasikan hubungan antar objek. Dalam graf, objek direpresentasikan sebagai titik yang disebut simpul (vertex) dan hubungan antar objek direpresentasikan sebagai garis yang disebut sisi (edge). Graf memiliki banyak aplikasi di berbagai bidang seperti ilmu komputer, jaringan sosial, dan kimia.

Contoh Soal Graf dan Penyelesaiannya

Berikut ini beberapa contoh soal graf beserta penyelesaiannya.

• Soal: Gambarlah graf yang merepresentasikan hubungan persahabatan di antara lima orang teman: A, B, C, D, dan E. Diketahui bahwa A berteman dengan B, C, dan D. B berteman dengan A, C, dan E. C berteman dengan A, B, dan D. D berteman dengan A dan C. E berteman dengan B.
  Penyelesaian:
  
  Diagram graf yang merepresentasikan hubungan persahabatan di antara lima orang teman tersebut adalah sebagai berikut:
  
  [Gambar ilustrasi graf yang menunjukkan simpul A, B, C, D, dan E, serta sisi yang menghubungkan simpul yang berteman. Misalnya, simpul A terhubung dengan simpul B, C, dan D, sedangkan simpul B terhubung dengan simpul A, C, dan E.]
• Soal: Tentukan derajat dari setiap simpul pada graf berikut:
  
  [Gambar ilustrasi graf dengan beberapa simpul dan sisi.]
  Penyelesaian:
  
  Derajat dari sebuah simpul adalah jumlah sisi yang terhubung dengan simpul tersebut.
  
  [Gambar ilustrasi graf dengan derajat setiap simpul ditandai. Misalnya, simpul A memiliki derajat 3 karena terhubung dengan 3 sisi.]

Contoh Soal Jalur dan Siklus dalam Graf

Jalur dalam graf adalah urutan simpul yang terhubung oleh sisi. Siklus adalah jalur tertutup, yaitu jalur yang dimulai dan berakhir pada simpul yang sama. Berikut ini contoh soal jalur dan siklus dalam graf.

• Soal: Tentukan jalur terpendek dari simpul A ke simpul E pada graf berikut:
  
  [Gambar ilustrasi graf dengan simpul A, B, C, D, dan E, serta sisi yang menghubungkan simpul-simpul tersebut.]
  Penyelesaian:
  
  Jalur terpendek dari simpul A ke simpul E adalah A-B-E.
• Soal: Tentukan siklus pada graf berikut:
  
  [Gambar ilustrasi graf dengan simpul A, B, C, D, dan E, serta sisi yang menghubungkan simpul-simpul tersebut.]
  Penyelesaian:
  
  Salah satu siklus pada graf tersebut adalah A-B-C-D-A.

Contoh Soal Pohon dalam Graf

Pohon adalah graf yang terhubung dan tidak memiliki siklus. Berikut ini contoh soal pohon dalam graf.

• Soal: Tentukan apakah graf berikut merupakan pohon:
  
  [Gambar ilustrasi graf dengan beberapa simpul dan sisi.]
  Penyelesaian:
  
  Graf tersebut bukan pohon karena memiliki siklus.
• Soal: Gambarlah pohon yang merepresentasikan struktur organisasi perusahaan dengan 5 karyawan.
  Penyelesaian:
  
  [Gambar ilustrasi pohon yang menunjukkan simpul-simpul yang merepresentasikan karyawan, dengan garis yang menghubungkan simpul yang menunjukkan hubungan hierarki di dalam perusahaan. Misalnya, simpul A (direktur) berada di puncak, dan simpul B, C, D, dan E (karyawan) berada di bawah simpul A.]

Contoh Soal Kombinatorika

Kombinatorika merupakan cabang matematika yang mempelajari tentang cara menghitung jumlah kemungkinan pengaturan atau susunan dari objek-objek tertentu. Dalam kombinatorika, kita akan mempelajari tentang permutasi, kombinasi, dan peluang. Permutasi dan kombinasi merupakan konsep dasar yang penting dalam memahami peluang.

Permutasi

Permutasi adalah pengaturan objek-objek yang urutannya diperhatikan. Rumus permutasi untuk memilih r objek dari n objek adalah:

_nP_r = n! / (n-r)!

dengan n! (faktorial n) = n x (n-1) x (n-2) x … x 2 x 1.

Contohnya, jika kita ingin menyusun 3 buku dari 5 buku yang berbeda, maka kita dapat menggunakan rumus permutasi.

• n = 5 (jumlah total buku)
• r = 3 (jumlah buku yang disusun)

Maka, jumlah cara menyusun 3 buku dari 5 buku yang berbeda adalah:

₅P₃ = 5! / (5-3)! = 5! / 2! = 5 x 4 x 3 = 60

Jadi, ada 60 cara berbeda untuk menyusun 3 buku dari 5 buku yang berbeda.

Kombinasi

Kombinasi adalah pemilihan objek-objek yang urutannya tidak diperhatikan. Rumus kombinasi untuk memilih r objek dari n objek adalah:

_nC_r = n! / (r! x (n-r)!)

Contohnya, jika kita ingin memilih 3 orang dari 5 orang untuk menjadi panitia, maka kita dapat menggunakan rumus kombinasi.

• n = 5 (jumlah total orang)
• r = 3 (jumlah orang yang dipilih)

Maka, jumlah cara memilih 3 orang dari 5 orang adalah:

₅C₃ = 5! / (3! x (5-3)!) = 5! / (3! x 2!) = 10

Jadi, ada 10 cara berbeda untuk memilih 3 orang dari 5 orang.

Peluang

Peluang adalah ukuran kemungkinan terjadinya suatu peristiwa. Rumus peluang adalah:

Peluang = Jumlah Kejadian yang Diinginkan / Jumlah Total Kejadian

Contohnya, jika kita melempar sebuah dadu, peluang munculnya mata dadu 6 adalah 1/6.

• Jumlah Kejadian yang Diinginkan = 1 (muncul mata dadu 6)
• Jumlah Total Kejadian = 6 (total mata dadu)

Maka, peluang munculnya mata dadu 6 adalah:

Peluang = 1 / 6

Jadi, peluang munculnya mata dadu 6 adalah 1/6.

Contoh Soal Algoritma

Algoritma merupakan serangkaian instruksi yang terstruktur dan logis yang digunakan untuk menyelesaikan suatu masalah. Dalam matematika diskrit, algoritma memiliki peran penting dalam berbagai bidang seperti pencarian, pengurutan, dan pemrosesan data.

Contoh Soal Algoritma Pencarian

Algoritma pencarian digunakan untuk menemukan elemen tertentu dalam suatu kumpulan data. Ada berbagai jenis algoritma pencarian, termasuk pencarian linier dan pencarian biner.

• Pencarian Linier: Pencarian linier merupakan algoritma pencarian yang sederhana. Algoritma ini memeriksa setiap elemen dalam kumpulan data secara berurutan hingga menemukan elemen yang dicari atau mencapai akhir kumpulan data.
• Pencarian Biner: Pencarian biner merupakan algoritma pencarian yang lebih efisien daripada pencarian linier. Algoritma ini hanya dapat digunakan pada kumpulan data yang telah diurutkan. Pencarian biner bekerja dengan membagi kumpulan data menjadi dua bagian secara berulang dan membandingkan elemen tengah dengan elemen yang dicari. Jika elemen tengah sama dengan elemen yang dicari, maka pencarian selesai. Jika elemen tengah lebih besar dari elemen yang dicari, maka pencarian dilanjutkan pada bagian kiri kumpulan data. Jika elemen tengah lebih kecil dari elemen yang dicari, maka pencarian dilanjutkan pada bagian kanan kumpulan data.

Contoh Soal:
Carilah angka 10 dalam kumpulan data berikut: [2, 5, 8, 10, 12, 15, 18].

Penyelesaian:
Pencarian Linier:
– Mulai dari elemen pertama (2).
– Bandingkan 2 dengan 10. Karena 2 tidak sama dengan 10, lanjutkan ke elemen berikutnya.
– Bandingkan 5 dengan 10. Karena 5 tidak sama dengan 10, lanjutkan ke elemen berikutnya.
– Bandingkan 8 dengan 10. Karena 8 tidak sama dengan 10, lanjutkan ke elemen berikutnya.
– Bandingkan 10 dengan 10. Karena 10 sama dengan 10, maka pencarian selesai.

Pencarian Biner:
– Karena kumpulan data telah diurutkan, kita dapat menggunakan pencarian biner.
– Elemen tengah dari kumpulan data adalah 10.
– Bandingkan 10 dengan 10. Karena 10 sama dengan 10, maka pencarian selesai.

Contoh Soal Algoritma Pengurutan

Algoritma pengurutan digunakan untuk mengurutkan elemen dalam suatu kumpulan data berdasarkan urutan tertentu, seperti urutan menaik atau menurun. Ada berbagai jenis algoritma pengurutan, termasuk bubble sort dan insertion sort.

• Bubble Sort: Bubble sort merupakan algoritma pengurutan yang sederhana. Algoritma ini bekerja dengan membandingkan setiap pasangan elemen yang berdekatan dan menukar elemen jika urutannya salah. Proses ini diulang hingga semua elemen terurut.
• Insertion Sort: Insertion sort merupakan algoritma pengurutan yang lebih efisien daripada bubble sort. Algoritma ini bekerja dengan membangun urutan yang terurut satu per satu. Algoritma ini mengambil elemen pertama dari kumpulan data yang tidak terurut dan menempatkannya di posisi yang benar dalam urutan yang terurut. Proses ini diulang hingga semua elemen terurut.

Contoh Soal:
Urutkan kumpulan data berikut menggunakan bubble sort dan insertion sort: [5, 2, 8, 1, 9].

Penyelesaian:
Bubble Sort:
– Mulai dari elemen pertama (5).
– Bandingkan 5 dengan 2. Karena 5 lebih besar dari 2, tukar kedua elemen tersebut. Kumpulan data sekarang menjadi [2, 5, 8, 1, 9].
– Bandingkan 5 dengan 8. Karena 5 lebih kecil dari 8, tidak perlu dilakukan penukaran.
– Bandingkan 8 dengan 1. Karena 8 lebih besar dari 1, tukar kedua elemen tersebut. Kumpulan data sekarang menjadi [2, 5, 1, 8, 9].
– Bandingkan 8 dengan 9. Karena 8 lebih kecil dari 9, tidak perlu dilakukan penukaran.
– Ulangi proses ini untuk semua elemen yang tersisa hingga semua elemen terurut. Kumpulan data yang terurut adalah [1, 2, 5, 8, 9].

Insertion Sort:
– Mulai dari elemen pertama (5).
– Ambil elemen kedua (2) dan tempatkan di posisi yang benar dalam urutan yang terurut. Kumpulan data sekarang menjadi [2, 5, 8, 1, 9].
– Ambil elemen ketiga (8) dan tempatkan di posisi yang benar dalam urutan yang terurut. Kumpulan data sekarang menjadi [2, 5, 8, 1, 9].
– Ambil elemen keempat (1) dan tempatkan di posisi yang benar dalam urutan yang terurut. Kumpulan data sekarang menjadi [1, 2, 5, 8, 9].
– Ambil elemen kelima (9) dan tempatkan di posisi yang benar dalam urutan yang terurut. Kumpulan data sekarang menjadi [1, 2, 5, 8, 9].

Contoh Soal Algoritma Rekursi

Algoritma rekursi merupakan algoritma yang memanggil dirinya sendiri. Algoritma rekursi sering digunakan untuk menyelesaikan masalah yang dapat dipecah menjadi sub-masalah yang lebih kecil.

• Faktorial: Faktorial dari suatu bilangan bulat positif adalah perkalian dari semua bilangan bulat positif dari 1 hingga bilangan bulat tersebut. Contohnya, faktorial dari 5 adalah 5! = 5 * 4 * 3 * 2 * 1 = 120.
• Fibonacci: Deret Fibonacci adalah deret bilangan bulat di mana setiap bilangan adalah jumlah dari dua bilangan sebelumnya. Deret Fibonacci dimulai dengan 0 dan 1. Contohnya, deret Fibonacci adalah 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …

Contoh Soal:
Hitunglah faktorial dari 5 dan carilah bilangan ke-10 dalam deret Fibonacci.

Penyelesaian:
Faktorial:
– Fungsi rekursi untuk menghitung faktorial:
“`
def factorial(n):
if n == 0:
return 1
else:
return n * factorial(n-1)
“`
– Panggil fungsi rekursi dengan n = 5:
“`
factorial(5)
“`
– Output: 120

Fibonacci:
– Fungsi rekursi untuk mencari bilangan ke-n dalam deret Fibonacci:
“`
def fibonacci(n):
if n <= 1:
return n
else:
return fibonacci(n-1) + fibonacci(n-2)
“`
– Panggil fungsi rekursi dengan n = 10:
“`
fibonacci(10)
“`
– Output: 55

Simpulan Akhir

Dengan memahami konsep-konsep matematika diskrit dan mempelajari contoh soal serta penyelesaiannya, Anda akan memiliki dasar yang kuat untuk mengaplikasikannya dalam berbagai bidang. Mulai dari pemrograman komputer hingga analisis data, matematika diskrit membuka peluang untuk memecahkan masalah-masalah yang menantang dan menciptakan solusi inovatif.