Contoh soal matematika teknik – Dunia teknik identik dengan perhitungan dan rumus yang rumit. Matematika teknik, cabang ilmu yang memadukan konsep matematika dengan aplikasi praktis dalam bidang teknik, menjadi kunci untuk memecahkan masalah kompleks di berbagai disiplin ilmu. Dari perencanaan struktur bangunan hingga merancang sistem elektronik, matematika teknik menjadi alat yang tak tergantikan.
Contoh Soal Matematika Teknik merupakan jembatan penghubung antara teori dan praktik, membantu mahasiswa teknik memahami bagaimana konsep-konsep matematika diaplikasikan dalam dunia nyata.
Pengertian Soal Matematika Teknik
Matematika teknik adalah cabang matematika yang mempelajari penerapan prinsip-prinsip matematika dalam memecahkan masalah teknik. Soal matematika teknik merupakan representasi dari masalah-masalah nyata yang dihadapi para insinyur dalam berbagai bidang teknik.
Pengertian Soal Matematika Teknik dalam Konteks Ilmu Teknik
Soal matematika teknik dirancang untuk membantu mahasiswa teknik memahami dan mengaplikasikan konsep matematika dalam konteks ilmu teknik. Soal-soal ini membantu mahasiswa mengembangkan kemampuan berpikir logis, analitis, dan sistematis dalam memecahkan masalah teknik. Selain itu, soal matematika teknik juga melatih mahasiswa untuk menafsirkan hasil perhitungan dalam konteks nyata dan mengambil keputusan yang tepat berdasarkan hasil analisis.
Perbedaan Soal Matematika Teknik dan Soal Matematika Umum
Soal matematika teknik memiliki beberapa perbedaan dengan soal matematika umum, yaitu:
- Soal matematika teknik berfokus pada aplikasi matematika dalam memecahkan masalah teknik, sedangkan soal matematika umum lebih bersifat teoritis dan abstrak.
- Soal matematika teknik biasanya melibatkan data nyata dan konteks yang spesifik, sedangkan soal matematika umum lebih sering menggunakan data dan konteks yang umum.
- Soal matematika teknik membutuhkan pemahaman tentang prinsip-prinsip teknik dan konsep-konsep matematika yang relevan, sedangkan soal matematika umum hanya membutuhkan pemahaman tentang konsep matematika.
Contoh Soal Matematika Teknik dalam Dunia Teknik
Berikut adalah contoh soal matematika teknik yang dijumpai dalam dunia teknik:
- Soal tentang Mekanika: Menghitung gaya yang dibutuhkan untuk mengangkat beban tertentu dengan menggunakan crane. Soal ini melibatkan konsep-konsep mekanika, seperti gaya, momen, dan keseimbangan.
- Soal tentang Kelistrikan: Menghitung arus listrik yang mengalir dalam suatu rangkaian listrik. Soal ini melibatkan konsep-konsep kelistrikan, seperti tegangan, arus, dan resistansi.
- Soal tentang Struktur: Menghitung beban maksimum yang dapat ditahan oleh suatu struktur jembatan. Soal ini melibatkan konsep-konsep mekanika material, seperti tegangan, regangan, dan modulus elastisitas.
Jenis-jenis Soal Matematika Teknik
Matematika teknik merupakan fondasi penting dalam berbagai bidang teknik. Memahami konsep-konsep matematika teknik sangatlah krusial untuk memecahkan masalah teknik yang kompleks. Soal-soal matematika teknik dirancang untuk menguji kemampuan mahasiswa dalam menerapkan prinsip-prinsip matematika untuk menyelesaikan masalah praktis di dunia teknik. Soal-soal ini biasanya menggabungkan konsep-konsep matematika dengan aplikasi teknik yang spesifik.
Jenis-jenis soal matematika teknik dapat diklasifikasikan berdasarkan bidang tekniknya. Setiap bidang teknik memiliki karakteristik dan tantangan tersendiri yang memerlukan pendekatan matematika yang spesifik.
Jenis-jenis Soal Matematika Teknik Berdasarkan Bidang Teknik
Berikut adalah tabel yang merangkum jenis-jenis soal matematika teknik dan contoh masing-masing jenis:
| Bidang Teknik | Jenis Soal | Contoh Soal |
|---|---|---|
| Teknik Sipil | Kalkulus, Aljabar Linear, Statistika | Menghitung momen inersia penampang balok beton, menganalisis tegangan dan regangan pada struktur, menentukan probabilitas kegagalan struktur |
| Teknik Elektro | Kalkulus, Persamaan Diferensial, Aljabar Linear | Menganalisis rangkaian listrik, menghitung medan elektromagnetik, merancang sistem kontrol elektronik |
| Teknik Mesin | Kalkulus, Persamaan Diferensial, Mekanika | Menghitung gaya dan momen pada sistem mekanik, menganalisis getaran dan stabilitas sistem, merancang mesin dan komponennya |
| Teknik Kimia | Kalkulus, Persamaan Diferensial, Kimia Fisika | Menghitung laju reaksi kimia, menganalisis kesetimbangan kimia, merancang proses kimia |
| Teknik Informatika | Algoritma dan Struktur Data, Probabilitas dan Statistika, Logika Matematika | Mendesain algoritma pencarian dan pengurutan data, menganalisis efisiensi algoritma, merancang sistem jaringan komputer |
Karakteristik dan Tingkat Kesulitan Soal Matematika Teknik, Contoh soal matematika teknik
Setiap jenis soal matematika teknik memiliki karakteristik dan tingkat kesulitan yang berbeda. Berikut adalah beberapa karakteristik umum:
- Kalkulus: Soal-soal kalkulus biasanya melibatkan konsep-konsep seperti turunan, integral, dan limit. Soal-soal ini seringkali digunakan untuk menganalisis perubahan dan perilaku sistem secara kontinu. Tingkat kesulitan soal kalkulus bervariasi, dari soal-soal dasar yang melibatkan operasi kalkulus sederhana hingga soal-soal yang lebih kompleks yang memerlukan pemahaman mendalam tentang konsep-konsep kalkulus.
- Aljabar Linear: Soal-soal aljabar linear biasanya melibatkan konsep-konsep seperti vektor, matriks, dan sistem persamaan linear. Soal-soal ini seringkali digunakan untuk menyelesaikan masalah-masalah geometri, menganalisis data, dan merancang sistem linear. Tingkat kesulitan soal aljabar linear bervariasi, dari soal-soal dasar yang melibatkan operasi matriks sederhana hingga soal-soal yang lebih kompleks yang memerlukan pemahaman mendalam tentang konsep-konsep aljabar linear.
- Persamaan Diferensial: Soal-soal persamaan diferensial biasanya melibatkan konsep-konsep seperti persamaan diferensial biasa dan persamaan diferensial parsial. Soal-soal ini seringkali digunakan untuk menganalisis sistem dinamis, menentukan solusi numerik, dan merancang model matematika untuk berbagai fenomena. Tingkat kesulitan soal persamaan diferensial bervariasi, dari soal-soal dasar yang melibatkan persamaan diferensial sederhana hingga soal-soal yang lebih kompleks yang memerlukan pemahaman mendalam tentang metode solusi numerik dan analitik.
- Statistika: Soal-soal statistika biasanya melibatkan konsep-konsep seperti probabilitas, distribusi probabilitas, uji hipotesis, dan regresi. Soal-soal ini seringkali digunakan untuk menganalisis data, menentukan probabilitas kejadian, dan merancang eksperimen. Tingkat kesulitan soal statistika bervariasi, dari soal-soal dasar yang melibatkan perhitungan probabilitas sederhana hingga soal-soal yang lebih kompleks yang memerlukan pemahaman mendalam tentang metode statistik.
Tingkat kesulitan soal matematika teknik juga dipengaruhi oleh faktor-faktor lain seperti:
- Kompleksitas masalah: Soal-soal yang melibatkan masalah-masalah kompleks dengan banyak variabel dan parameter cenderung lebih sulit.
- Tingkat abstraksi: Soal-soal yang melibatkan konsep-konsep abstrak yang sulit dipahami cenderung lebih sulit.
- Penggunaan software: Soal-soal yang memerlukan penggunaan software khusus untuk menyelesaikan masalah cenderung lebih sulit.
Contoh Soal Matematika Teknik
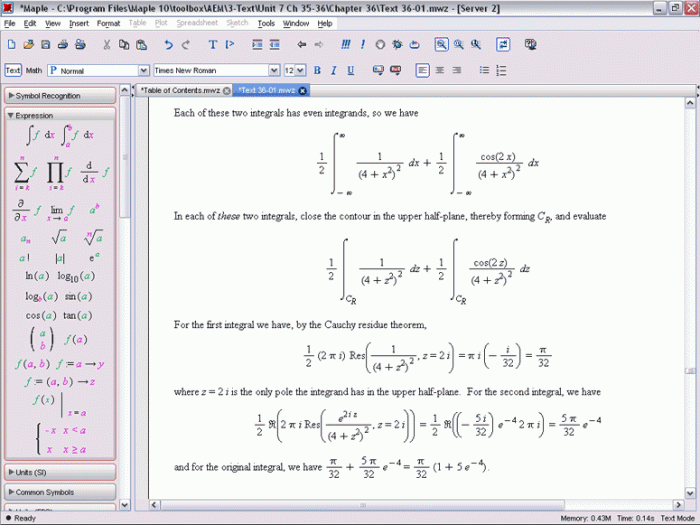
Matematika teknik merupakan bidang penting yang mendasari berbagai disiplin ilmu teknik. Pemahaman konsep matematika seperti kalkulus, aljabar linear, dan persamaan diferensial sangat krusial dalam memecahkan masalah-masalah teknik yang kompleks. Berikut ini beberapa contoh soal matematika teknik yang menunjukkan penerapan konsep-konsep tersebut dalam berbagai bidang teknik.
Kalkulus
Kalkulus adalah cabang matematika yang mempelajari tentang perubahan dan akumulasi. Dalam teknik, kalkulus digunakan untuk menganalisis gerakan, perubahan suhu, dan berbagai fenomena dinamis lainnya.
- Contoh soal: Sebuah benda bergerak dengan kecepatan v(t) = 2t^2 + 3t meter per detik. Tentukan jarak yang ditempuh benda selama 5 detik pertama.
- Penyelesaian: Jarak yang ditempuh benda sama dengan integral dari kecepatan terhadap waktu.
Jarak = ∫v(t) dt = ∫(2t^2 + 3t) dt = (2/3)t^3 + (3/2)t^2 + C
Karena benda mulai bergerak dari titik nol, maka C = 0. Jarak yang ditempuh selama 5 detik pertama adalah:
Jarak = (2/3)(5)^3 + (3/2)(5)^2 = 166,67 meter
Aljabar Linear
Aljabar linear merupakan cabang matematika yang mempelajari tentang vektor, matriks, dan sistem persamaan linear. Dalam teknik, aljabar linear digunakan untuk menganalisis struktur, transformasi, dan sistem persamaan linear yang sering muncul dalam berbagai bidang teknik.
- Contoh soal: Sebuah perusahaan memproduksi dua jenis produk, A dan B. Setiap produk membutuhkan bahan baku X dan Y. Untuk memproduksi satu unit produk A dibutuhkan 2 unit bahan baku X dan 3 unit bahan baku Y. Untuk memproduksi satu unit produk B dibutuhkan 4 unit bahan baku X dan 1 unit bahan baku Y. Jika perusahaan memiliki 100 unit bahan baku X dan 80 unit bahan baku Y, tentukan jumlah maksimum produk A dan B yang dapat diproduksi.
- Penyelesaian: Soal ini dapat diselesaikan dengan menggunakan konsep sistem persamaan linear.
2A + 4B ≤ 100 (persamaan bahan baku X)
3A + B ≤ 80 (persamaan bahan baku Y)
A ≥ 0, B ≥ 0 (kendala non-negatif)Untuk mencari solusi optimal, dapat digunakan metode grafik atau metode Simplex. Solusi optimal adalah A = 20 dan B = 15. Artinya, perusahaan dapat memproduksi maksimal 20 unit produk A dan 15 unit produk B.
Persamaan Diferensial
Persamaan diferensial adalah persamaan yang melibatkan turunan fungsi. Dalam teknik, persamaan diferensial digunakan untuk memodelkan berbagai fenomena dinamis seperti aliran fluida, getaran, dan rangkaian listrik.
- Contoh soal: Sebuah benda bermassa 1 kg digantungkan pada pegas dengan konstanta pegas k = 10 N/m. Benda ditarik ke bawah sejauh 0,1 meter dari posisi setimbangnya dan kemudian dilepaskan. Tentukan persamaan gerak benda.
- Penyelesaian: Persamaan gerak benda dapat dimodelkan dengan persamaan diferensial berikut:
m d^2x/dt^2 + kx = 0
Dimana m adalah massa benda, k adalah konstanta pegas, dan x adalah perpindahan benda dari posisi setimbangnya. Substitusikan nilai m dan k, diperoleh:
d^2x/dt^2 + 10x = 0
Solusi umum persamaan diferensial ini adalah:
x(t) = A cos(ωt) + B sin(ωt)
Dimana A dan B adalah konstanta integrasi, dan ω = √(k/m) adalah frekuensi sudut. Dari kondisi awal, diperoleh A = 0,1 dan B = 0. Jadi, persamaan gerak benda adalah:
x(t) = 0,1 cos(√10t)
Manfaat Soal Matematika Teknik: Contoh Soal Matematika Teknik
Soal matematika teknik merupakan bagian penting dalam pembelajaran teknik. Selain menguji pemahaman konsep, soal-soal ini memiliki peran vital dalam mengembangkan kemampuan yang dibutuhkan para calon insinyur untuk menghadapi tantangan dunia nyata.
Manfaat Belajar Soal Matematika Teknik
Berikut beberapa manfaat mempelajari soal matematika teknik bagi mahasiswa teknik:
- Meningkatkan Kemampuan Pemecahan Masalah: Soal matematika teknik dirancang untuk melatih kemampuan berpikir logis dan analitis dalam memecahkan masalah. Melalui latihan soal, mahasiswa dibekali dengan strategi dan teknik untuk mengidentifikasi masalah, merumuskan solusi, dan mengevaluasi hasil.
- Memperkuat Fondasi Matematika: Soal matematika teknik membantu mahasiswa untuk mengaplikasikan konsep matematika dasar dalam konteks teknik. Dengan demikian, pemahaman mereka terhadap materi matematika menjadi lebih kuat dan tertanam.
- Mengembangkan Keterampilan Berpikir Kritis: Soal matematika teknik seringkali menuntut mahasiswa untuk berpikir kritis dan mencari solusi yang optimal. Mereka harus mampu menganalisis informasi, mengevaluasi berbagai pilihan, dan mengambil keputusan yang tepat.
- Meningkatkan Kemampuan Komunikasi Teknik: Soal matematika teknik seringkali mengharuskan mahasiswa untuk menjelaskan solusi dan proses berpikir mereka secara logis dan sistematis. Hal ini membantu mereka mengembangkan kemampuan komunikasi teknik yang penting dalam dunia kerja.
Soal Matematika Teknik dan Kemampuan Berpikir Logis dan Analitis
Soal matematika teknik berperan penting dalam mengembangkan kemampuan berpikir logis dan analitis. Melalui latihan soal, mahasiswa dilatih untuk:
- Mengidentifikasi Pola dan Hubungan: Soal matematika teknik seringkali melibatkan pola dan hubungan matematis yang kompleks. Dengan menyelesaikan soal, mahasiswa belajar untuk mengenali pola dan hubungan tersebut, yang penting dalam memahami dan menganalisis data teknik.
- Membangun Argumentasi Logis: Soal matematika teknik mengharuskan mahasiswa untuk membangun argumentasi logis dan sistematis dalam memecahkan masalah. Mereka harus mampu menjelaskan langkah-langkah yang mereka ambil dan alasan di baliknya.
- Menerapkan Prinsip Logika: Soal matematika teknik melibatkan penerapan prinsip-prinsip logika dalam menyelesaikan masalah. Mahasiswa belajar untuk berpikir secara deduktif dan induktif, serta memahami hubungan sebab-akibat.
Contoh Penerapan Soal Matematika Teknik dalam Masalah Teknik
Soal matematika teknik memiliki aplikasi yang luas dalam berbagai bidang teknik. Berikut contoh konkret bagaimana soal matematika teknik membantu dalam memecahkan masalah teknik di dunia nyata:
- Teknik Sipil: Soal matematika teknik digunakan untuk merancang struktur bangunan yang aman dan efisien. Misalnya, soal tentang tegangan dan regangan membantu insinyur sipil untuk menentukan kekuatan dan stabilitas jembatan atau gedung.
- Teknik Elektro: Soal matematika teknik digunakan untuk menganalisis dan merancang sistem kelistrikan. Misalnya, soal tentang arus dan tegangan membantu insinyur elektro untuk memahami dan merancang sirkuit listrik yang aman dan efisien.
- Teknik Mesin: Soal matematika teknik digunakan untuk merancang dan menganalisis mesin. Misalnya, soal tentang dinamika membantu insinyur mesin untuk memahami gerakan dan perilaku mesin, sehingga dapat merancang mesin yang optimal dan efisien.
Tips Mengerjakan Soal Matematika Teknik
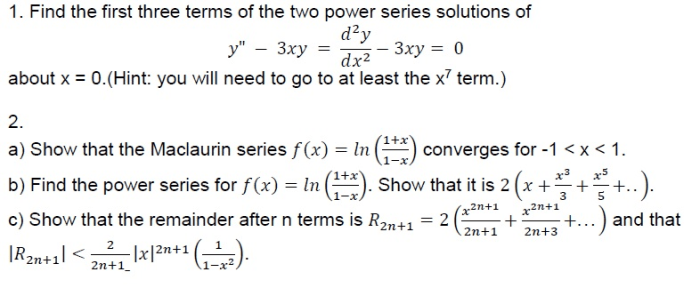
Matematika teknik adalah salah satu mata kuliah yang cukup menantang bagi mahasiswa teknik. Untuk sukses dalam mata kuliah ini, diperlukan pemahaman konsep yang kuat dan strategi efektif dalam menyelesaikan soal. Artikel ini akan membahas beberapa tips dan strategi yang dapat membantu Anda dalam menghadapi soal-soal matematika teknik.
Memahami Konsep Dasar Matematika
Sebelum Anda mulai mengerjakan soal matematika teknik, penting untuk memahami konsep dasar matematika yang mendasari topik tersebut. Konsep dasar ini meliputi aljabar, kalkulus, trigonometri, dan geometri. Pastikan Anda memiliki pemahaman yang kuat tentang konsep-konsep ini sebelum Anda mencoba untuk menyelesaikan soal yang lebih kompleks.
Langkah-Langkah Sistematis dalam Menyelesaikan Soal Matematika Teknik
Untuk menyelesaikan soal matematika teknik dengan tepat, penting untuk mengikuti langkah-langkah sistematis yang terstruktur. Berikut adalah langkah-langkah yang dapat Anda ikuti:
- Pahami Soal: Baca soal dengan cermat dan pahami apa yang ditanyakan. Identifikasi variabel yang diketahui dan yang tidak diketahui.
- Buat Diagram: Jika memungkinkan, buatlah diagram atau sketsa untuk membantu Anda memvisualisasikan masalah. Diagram dapat membantu Anda memahami hubungan antara variabel yang terlibat.
- Tentukan Rumus yang Tepat: Pilih rumus yang tepat untuk menyelesaikan masalah berdasarkan konsep matematika yang terlibat.
- Selesaikan Persamaan: Substitusikan nilai yang diketahui ke dalam rumus dan selesaikan persamaan untuk menemukan nilai yang tidak diketahui.
- Verifikasi Jawaban: Setelah Anda mendapatkan jawaban, verifikasi jawaban Anda untuk memastikan bahwa jawaban tersebut masuk akal dan sesuai dengan konteks soal.
Strategi Efektif untuk Menyelesaikan Soal Matematika Teknik
Berikut adalah beberapa strategi efektif yang dapat membantu Anda dalam menyelesaikan soal matematika teknik:
- Latihan Terus-Menerus: Latihan adalah kunci untuk menguasai matematika teknik. Semakin banyak Anda berlatih, semakin baik Anda akan memahami konsep dan strategi yang terlibat.
- Cari Bantuan Jika Dibutuhkan: Jangan ragu untuk meminta bantuan dari dosen, asisten dosen, atau teman sekelas jika Anda mengalami kesulitan dalam memahami konsep atau menyelesaikan soal.
- Manfaatkan Sumber Daya yang Tersedia: Manfaatkan sumber daya yang tersedia, seperti buku teks, buku latihan, dan situs web pendidikan, untuk membantu Anda belajar dan memahami konsep matematika teknik.
- Kerjakan Soal dengan Metode yang Berbeda: Cobalah untuk menyelesaikan soal dengan metode yang berbeda untuk memastikan bahwa Anda memahami konsep dari berbagai sudut pandang.
Tips Tambahan untuk Mengerjakan Soal Matematika Teknik
Berikut adalah beberapa tips tambahan yang dapat membantu Anda dalam mengerjakan soal matematika teknik:
- Manfaatkan Kalkulator: Kalkulator dapat membantu Anda menyelesaikan soal dengan lebih cepat dan akurat, terutama untuk soal yang melibatkan perhitungan yang kompleks.
- Perhatikan Satuan: Pastikan Anda menggunakan satuan yang tepat dalam semua perhitungan Anda. Kesalahan dalam penggunaan satuan dapat menyebabkan kesalahan dalam jawaban Anda.
- Organisir Pekerjaan Anda: Organisir pekerjaan Anda dengan rapi dan terstruktur. Ini akan membantu Anda untuk menghindari kesalahan dan memudahkan Anda untuk memeriksa kembali pekerjaan Anda.
- Manajemen Waktu: Alokasikan waktu yang cukup untuk menyelesaikan setiap soal. Jangan terburu-buru dan pastikan Anda memiliki cukup waktu untuk memeriksa kembali pekerjaan Anda.
Ringkasan Terakhir

Memahami contoh soal matematika teknik tidak hanya membantu mahasiswa teknik dalam menyelesaikan tugas kuliah, tetapi juga membekali mereka dengan kemampuan berpikir logis dan analitis yang penting dalam mengatasi tantangan di dunia profesional. Dengan kemampuan memahami dan mengaplikasikan matematika teknik, para insinyur dapat menciptakan inovasi yang bermanfaat bagi manusia dan lingkungan.






