Contoh soal matriks beserta jawabannya – Matriks, sebuah susunan bilangan yang tersusun dalam baris dan kolom, mungkin terdengar menakutkan bagi sebagian orang. Tapi, jangan khawatir! Matriks sebenarnya adalah alat yang sangat berguna dalam matematika dan memiliki banyak aplikasi di berbagai bidang, seperti ekonomi, fisika, dan komputer. Dalam artikel ini, kita akan menjelajahi dunia matriks dengan membahas pengertian, operasi, dan contoh soal yang disertai jawabannya. Siap untuk menguasai konsep matriks?
Melalui contoh soal matriks beserta jawabannya, Anda akan memahami bagaimana operasi-operasi matriks seperti penjumlahan, pengurangan, perkalian, dan determinan dilakukan. Selain itu, Anda juga akan mempelajari bagaimana matriks dapat digunakan untuk menyelesaikan sistem persamaan linear dan berbagai permasalahan di dunia nyata.
Pengertian Matriks: Contoh Soal Matriks Beserta Jawabannya
Matriks dalam matematika adalah kumpulan bilangan yang disusun dalam bentuk baris dan kolom. Bayangkan matriks seperti tabel, tetapi dengan aturan khusus untuk operasi matematika. Matriks memiliki peran penting dalam berbagai bidang, seperti aljabar linear, persamaan linear, dan bahkan ilmu komputer.
Contoh Matriks
Berikut beberapa contoh matriks dengan berbagai jenis dan ukuran:
- Matriks 2×2:
1 2 3 4 - Matriks 3×3:
1 2 3 4 5 6 7 8 9 - Matriks 2×3:
1 2 3 4 5 6
Perbedaan Matriks Baris, Matriks Kolom, dan Matriks Persegi
Ada beberapa jenis matriks yang perlu kita ketahui:
- Matriks Baris: Matriks dengan hanya satu baris, seperti:
1 2 3 4 - Matriks Kolom: Matriks dengan hanya satu kolom, seperti:
1 2 3 4 - Matriks Persegi: Matriks dengan jumlah baris dan kolom yang sama, seperti contoh matriks 2×2 dan 3×3 di atas.
Invers Matriks
Invers matriks merupakan konsep penting dalam aljabar linear. Invers matriks, dilambangkan dengan A⁻¹, adalah matriks yang ketika dikalikan dengan matriks aslinya (A), menghasilkan matriks identitas (I). Matriks identitas adalah matriks persegi dengan diagonal utama berisi 1 dan elemen lainnya 0.
Menghitung Invers Matriks 2×2
Invers matriks 2×2 dapat dihitung dengan rumus berikut:
A⁻¹ = 1 / det(A) * [d -b]
[-c a]
Dimana:
* A = matriks 2×2 dengan elemen [a b]
[c d]
* det(A) = determinan matriks A, dihitung dengan rumus ad – bc.
* A⁻¹ = invers matriks A.
Jika det(A) = 0, maka matriks A tidak memiliki invers.
Menghitung Invers Matriks 3×3
Menghitung invers matriks 3×3 lebih rumit dan melibatkan beberapa langkah. Berikut adalah langkah-langkahnya:
1. Hitung determinan matriks A.
2. Tulis matriks kofaktor dari A. Kofaktor dari elemen aij adalah (-1)i+j kali determinan matriks minor yang didapat dengan menghapus baris i dan kolom j dari A.
3. Transpose matriks kofaktor untuk mendapatkan matriks adjoin dari A.
4. Bagi matriks adjoin dengan determinan A untuk mendapatkan invers matriks A.
Contoh Soal Invers Matriks
Soal:
Tentukan invers dari matriks berikut:
A = [2 1]
[4 3]
Jawaban:
1. Hitung determinan A: det(A) = (2 * 3) – (1 * 4) = 2.
2. Tulis matriks kofaktor dari A:
[3 -1]
[-4 2]
3. Transpose matriks kofaktor:
[3 -4]
[-1 2]
4. Bagi matriks adjoin dengan determinan A:
A⁻¹ = 1/2 * [3 -4]
[-1 2]
A⁻¹ = [3/2 -2]
[-1/2 1]
Jadi, invers dari matriks A adalah [3/2 -2]
[-1/2 1]
Sistem Persamaan Linear
Sistem persamaan linear adalah kumpulan persamaan linear yang memiliki variabel yang sama. Matriks dapat digunakan untuk menyelesaikan sistem persamaan linear dengan cara yang lebih terstruktur dan efisien.
Representasi Matriks
Sistem persamaan linear dapat direpresentasikan dalam bentuk matriks. Matriks koefisien berisi koefisien dari setiap variabel dalam setiap persamaan, sedangkan vektor konstanta berisi konstanta pada setiap persamaan. Vektor variabel berisi variabel-variabel yang tidak diketahui.
Contoh Soal Sistem Persamaan Linear
Sistem Persamaan Linear dengan 2 Variabel
Misalkan kita memiliki sistem persamaan linear berikut:
“`
2x + 3y = 7
x – y = 1
“`
Sistem persamaan linear ini dapat direpresentasikan dalam bentuk matriks sebagai berikut:
“`
[ 2 3 ] [ x ] = [ 7 ]
[ 1 -1 ] [ y ] = [ 1 ]
“`
Sistem Persamaan Linear dengan 3 Variabel
Misalkan kita memiliki sistem persamaan linear berikut:
“`
x + 2y – z = 3
2x – y + 3z = 1
3x + y + 2z = 4
“`
Sistem persamaan linear ini dapat direpresentasikan dalam bentuk matriks sebagai berikut:
“`
[ 1 2 -1 ] [ x ] = [ 3 ]
[ 2 -1 3 ] [ y ] = [ 1 ]
[ 3 1 2 ] [ z ] = [ 4 ]
“`
Metode Matriks untuk Menyelesaikan Sistem Persamaan Linear
Ada beberapa metode matriks yang dapat digunakan untuk menyelesaikan sistem persamaan linear, antara lain:
- Metode Eliminasi Gauss
- Metode Eliminasi Gauss-Jordan
- Metode Invers Matriks
- Metode Cramer
Metode Eliminasi Gauss
Metode eliminasi Gauss adalah metode yang digunakan untuk menyelesaikan sistem persamaan linear dengan mengubah matriks koefisien menjadi bentuk eselon baris. Bentuk eselon baris adalah bentuk matriks di mana elemen pertama pada setiap baris adalah 1, dan elemen di bawah elemen pertama pada setiap baris adalah 0.
Langkah-langkah Metode Eliminasi Gauss
1. Tulis sistem persamaan linear dalam bentuk matriks.
2. Lakukan operasi baris elementer pada matriks koefisien untuk mengubahnya menjadi bentuk eselon baris.
3. Setelah matriks koefisien dalam bentuk eselon baris, selesaikan sistem persamaan linear dengan menggunakan substitusi mundur.
Contoh Soal
Selesaikan sistem persamaan linear berikut dengan menggunakan metode eliminasi Gauss:
“`
2x + 3y = 7
x – y = 1
“`
1. Tulis sistem persamaan linear dalam bentuk matriks:
“`
[ 2 3 ] [ x ] = [ 7 ]
[ 1 -1 ] [ y ] = [ 1 ]
“`
2. Lakukan operasi baris elementer pada matriks koefisien untuk mengubahnya menjadi bentuk eselon baris:
“`
[ 1 -1 ] [ x ] = [ 1 ]
[ 0 5 ] [ y ] = [ 5 ]
“`
3. Selesaikan sistem persamaan linear dengan menggunakan substitusi mundur:
“`
y = 1
x = 2
“`
Jadi, solusi dari sistem persamaan linear adalah x = 2 dan y = 1.
Metode Eliminasi Gauss-Jordan
Metode eliminasi Gauss-Jordan adalah metode yang digunakan untuk menyelesaikan sistem persamaan linear dengan mengubah matriks koefisien menjadi bentuk eselon baris tereduksi. Bentuk eselon baris tereduksi adalah bentuk matriks di mana elemen pertama pada setiap baris adalah 1, elemen di bawah elemen pertama pada setiap baris adalah 0, dan elemen di atas elemen pertama pada setiap baris juga adalah 0.
Langkah-langkah Metode Eliminasi Gauss-Jordan
1. Tulis sistem persamaan linear dalam bentuk matriks.
2. Lakukan operasi baris elementer pada matriks koefisien untuk mengubahnya menjadi bentuk eselon baris tereduksi.
3. Setelah matriks koefisien dalam bentuk eselon baris tereduksi, solusi dari sistem persamaan linear dapat langsung dibaca dari matriks.
Contoh Soal
Selesaikan sistem persamaan linear berikut dengan menggunakan metode eliminasi Gauss-Jordan:
“`
2x + 3y = 7
x – y = 1
“`
1. Tulis sistem persamaan linear dalam bentuk matriks:
“`
[ 2 3 ] [ x ] = [ 7 ]
[ 1 -1 ] [ y ] = [ 1 ]
“`
2. Lakukan operasi baris elementer pada matriks koefisien untuk mengubahnya menjadi bentuk eselon baris tereduksi:
“`
[ 1 0 ] [ x ] = [ 2 ]
[ 0 1 ] [ y ] = [ 1 ]
“`
3. Solusi dari sistem persamaan linear dapat langsung dibaca dari matriks:
“`
x = 2
y = 1
“`
Jadi, solusi dari sistem persamaan linear adalah x = 2 dan y = 1.
Metode Invers Matriks
Metode invers matriks adalah metode yang digunakan untuk menyelesaikan sistem persamaan linear dengan menggunakan invers dari matriks koefisien. Invers dari matriks A adalah matriks A-1 yang memenuhi persamaan A A-1 = I, di mana I adalah matriks identitas.
Langkah-langkah Metode Invers Matriks
1. Tulis sistem persamaan linear dalam bentuk matriks.
2. Hitung invers dari matriks koefisien.
3. Kalikan invers dari matriks koefisien dengan vektor konstanta untuk mendapatkan solusi dari sistem persamaan linear.
Contoh Soal
Selesaikan sistem persamaan linear berikut dengan menggunakan metode invers matriks:
“`
2x + 3y = 7
x – y = 1
“`
1. Tulis sistem persamaan linear dalam bentuk matriks:
“`
[ 2 3 ] [ x ] = [ 7 ]
[ 1 -1 ] [ y ] = [ 1 ]
“`
2. Hitung invers dari matriks koefisien:
“`
[ 2 3 ]-1 = [ -1/5 3/5 ]
[ 1 -1 ] [ 1/5 2/5 ]
“`
3. Kalikan invers dari matriks koefisien dengan vektor konstanta:
“`
[ -1/5 3/5 ] [ 7 ] = [ 2 ]
[ 1/5 2/5 ] [ 1 ] = [ 1 ]
“`
Jadi, solusi dari sistem persamaan linear adalah x = 2 dan y = 1.
Metode Cramer, Contoh soal matriks beserta jawabannya
Metode Cramer adalah metode yang digunakan untuk menyelesaikan sistem persamaan linear dengan menggunakan determinan matriks. Determinan dari matriks A adalah nilai skalar yang dihitung dari elemen-elemen matriks A.
Langkah-langkah Metode Cramer
1. Tulis sistem persamaan linear dalam bentuk matriks.
2. Hitung determinan dari matriks koefisien.
3. Hitung determinan dari matriks yang diperoleh dengan mengganti kolom ke-i dari matriks koefisien dengan vektor konstanta.
4. Solusi dari sistem persamaan linear adalah xi = det(Ai)/det(A), di mana Ai adalah matriks yang diperoleh dengan mengganti kolom ke-i dari matriks koefisien dengan vektor konstanta.
Contoh Soal
Selesaikan sistem persamaan linear berikut dengan menggunakan metode Cramer:
“`
2x + 3y = 7
x – y = 1
“`
1. Tulis sistem persamaan linear dalam bentuk matriks:
“`
[ 2 3 ] [ x ] = [ 7 ]
[ 1 -1 ] [ y ] = [ 1 ]
“`
2. Hitung determinan dari matriks koefisien:
“`
det(A) = (2)(-1) – (3)(1) = -5
“`
3. Hitung determinan dari matriks yang diperoleh dengan mengganti kolom ke-1 dari matriks koefisien dengan vektor konstanta:
“`
det(A1) = (7)(-1) – (3)(1) = -10
“`
4. Hitung determinan dari matriks yang diperoleh dengan mengganti kolom ke-2 dari matriks koefisien dengan vektor konstanta:
“`
det(A2) = (2)(1) – (7)(1) = -5
“`
5. Solusi dari sistem persamaan linear adalah:
“`
x = det(A1)/det(A) = -10/-5 = 2
y = det(A2)/det(A) = -5/-5 = 1
“`
Jadi, solusi dari sistem persamaan linear adalah x = 2 dan y = 1.
Penerapan Matriks dalam Kehidupan Sehari-hari
Matriks, dalam matematika, adalah susunan bilangan yang disusun dalam baris dan kolom. Meskipun mungkin terlihat abstrak, matriks memiliki banyak aplikasi praktis dalam berbagai bidang kehidupan sehari-hari. Dari bidang ekonomi hingga fisika dan komputer, matriks menjadi alat penting dalam memecahkan masalah dan menganalisis data.
Penerapan Matriks dalam Ekonomi
Dalam bidang ekonomi, matriks digunakan untuk menganalisis data pasar dan membuat prediksi. Salah satu contohnya adalah dalam analisis input-output, yang digunakan untuk mempelajari hubungan antar sektor ekonomi. Matriks input-output menunjukkan berapa banyak output dari satu sektor yang digunakan sebagai input oleh sektor lainnya. Dengan menggunakan matriks ini, para ekonom dapat menganalisis dampak perubahan pada satu sektor terhadap sektor lainnya.
Mencari contoh soal matriks beserta jawabannya? Nah, selain materi matriks, kamu juga bisa belajar tentang kalimat perintah atau imperative sentence. Contoh soal imperative sentence bisa membantumu memahami struktur kalimat yang digunakan untuk memberikan instruksi atau permintaan. Setelah mempelajari soal imperative sentence, kamu bisa kembali fokus pada contoh soal matriks dan mengasah kemampuanmu dalam menyelesaikannya.
- Contohnya, dalam analisis input-output, matriks dapat menunjukkan berapa banyak kayu yang dibutuhkan untuk membuat meja, berapa banyak meja yang dibutuhkan untuk membuat rumah, dan berapa banyak rumah yang dibutuhkan untuk membangun kota. Dengan menggunakan matriks ini, para ekonom dapat mempelajari bagaimana perubahan dalam produksi kayu akan berdampak pada produksi meja, rumah, dan akhirnya, pertumbuhan kota.
Penerapan Matriks dalam Fisika
Matriks juga memiliki aplikasi yang luas dalam fisika, terutama dalam menyelesaikan masalah gerak dan mekanika kuantum. Matriks digunakan untuk merepresentasikan transformasi linear, yang memungkinkan kita untuk menggambarkan bagaimana suatu objek bergerak dalam ruang. Matriks juga digunakan dalam mekanika kuantum untuk merepresentasikan operator kuantum, yang menggambarkan sifat-sifat partikel.
- Misalnya, dalam mekanika klasik, matriks dapat digunakan untuk menggambarkan rotasi objek di sekitar sumbu tertentu. Dengan menggunakan matriks rotasi, kita dapat menentukan posisi objek setelah rotasi. Dalam mekanika kuantum, matriks digunakan untuk menggambarkan operator momentum, yang mengukur momentum suatu partikel.
Penerapan Matriks dalam Komputer
Dalam bidang komputer, matriks digunakan dalam berbagai algoritma pemrosesan gambar, seperti transformasi gambar, kompresi gambar, dan pengenalan pola. Matriks digunakan untuk merepresentasikan gambar sebagai kumpulan piksel, dan operasi matriks digunakan untuk memanipulasi gambar.
- Contohnya, dalam transformasi gambar, matriks digunakan untuk mengubah ukuran, memutar, atau memiringkan gambar. Dalam kompresi gambar, matriks digunakan untuk mengurangi ukuran file gambar tanpa mengurangi kualitas gambar secara signifikan. Dalam pengenalan pola, matriks digunakan untuk mengidentifikasi pola dalam gambar, seperti wajah manusia atau objek tertentu.
Soal Latihan Matriks
Materi matriks merupakan salah satu materi matematika yang cukup penting. Matriks merupakan susunan bilangan yang disusun dalam baris dan kolom. Operasi matriks meliputi penjumlahan, pengurangan, perkalian, dan determinan. Untuk memahami materi matriks dengan baik, kamu bisa berlatih mengerjakan soal-soal latihan.
Soal Latihan Operasi Matriks
Berikut beberapa contoh soal latihan operasi matriks:
| No | Soal | Jawaban |
|---|---|---|
| 1 | Tentukan hasil penjumlahan matriks A + B, jika: A = '[ 1 2 ]' '[ 3 4 ]' B = '[ 5 6 ]' '[ 7 8 ]' |
'[ 6 8 ]' '[ 10 12 ]' |
| 2 | Tentukan hasil pengurangan matriks C – D, jika: C = '[ 9 10 ]' '[ 11 12 ]' D = '[ 1 2 ]' '[ 3 4 ]' |
'[ 8 8 ]' '[ 8 8 ]' |
| 3 | Tentukan hasil perkalian matriks E x F, jika: E = '[ 2 3 ]' '[ 4 5 ]' F = '[ 6 7 ]' '[ 8 9 ]' |
'[ 36 41 ]' '[ 62 71 ]' |
| 4 | Tentukan hasil perkalian skalar 2 x G, jika: G = '[ 1 2 ]' '[ 3 4 ]' |
'[ 2 4 ]' '[ 6 8 ]' |
| 5 | Tentukan hasil penjumlahan matriks H + I, jika: H = '[ 1 2 3 ]' '[ 4 5 6 ]' I = '[ 7 8 9 ]' '[ 10 11 12 ]' |
'[ 8 10 12 ]' '[ 14 16 18 ]' |
Soal Latihan Determinan Matriks
Determinan matriks adalah suatu nilai skalar yang dapat dihitung dari matriks persegi. Berikut beberapa contoh soal latihan determinan matriks:
| No | Soal | Jawaban |
|---|---|---|
| 1 | Tentukan determinan matriks J, jika: J = '[ 2 3 ]' '[ 4 5 ]' |
Det (J) = (2 x 5) – (3 x 4) = -2 |
| 2 | Tentukan determinan matriks K, jika: K = '[ 1 2 3 ]' '[ 4 5 6 ]' '[ 7 8 9 ]' |
Det (K) = 1((5 x 9) – (6 x 8)) – 2((4 x 9) – (6 x 7)) + 3((4 x 8) – (5 x 7)) = 0 |
| 3 | Tentukan determinan matriks L, jika: L = '[ 1 2 ]' '[ 3 4 ]' |
Det (L) = (1 x 4) – (2 x 3) = -2 |
| 4 | Tentukan determinan matriks M, jika: M = '[ 1 0 0 ]' '[ 0 1 0 ]' '[ 0 0 1 ]' |
Det (M) = 1((1 x 1) – (0 x 0)) – 0((0 x 1) – (0 x 0)) + 0((0 x 0) – (1 x 0)) = 1 |
| 5 | Tentukan determinan matriks N, jika: N = '[ 2 1 ]' '[ 4 3 ]' |
Det (N) = (2 x 3) – (1 x 4) = 2 |
Soal Latihan Invers Matriks
Invers matriks adalah matriks yang jika dikalikan dengan matriks aslinya akan menghasilkan matriks identitas. Berikut beberapa contoh soal latihan invers matriks:
| No | Soal | Jawaban |
|---|---|---|
| 1 | Tentukan invers matriks O, jika: O = '[ 2 3 ]' '[ 4 5 ]' |
O-1 = '[ 5 -3 ]' '[ -4 2 ]' |
| 2 | Tentukan invers matriks P, jika: P = '[ 1 2 ]' '[ 3 4 ]' |
P-1 = '[ -2 1 ]' '[ 1.5 -0.5 ]' |
| 3 | Tentukan invers matriks Q, jika: Q = '[ 1 0 0 ]' '[ 0 1 0 ]' '[ 0 0 1 ]' |
Q-1 = '[ 1 0 0 ]' '[ 0 1 0 ]' '[ 0 0 1 ]' |
| 4 | Tentukan invers matriks R, jika: R = '[ 2 1 ]' '[ 4 3 ]' |
R-1 = '[ 1.5 -0.5 ]' '[ -2 1 ]' |
| 5 | Tentukan invers matriks S, jika: S = '[ 1 2 3 ]' '[ 4 5 6 ]' '[ 7 8 9 ]' |
Matriks S tidak memiliki invers karena determinannya sama dengan 0. |
Contoh Soal Matriks dan Jawaban
Matriks adalah kumpulan bilangan yang disusun dalam baris dan kolom. Setiap bilangan dalam matriks disebut elemen matriks. Matriks banyak digunakan dalam berbagai bidang, seperti matematika, fisika, ekonomi, dan komputer.
Dalam artikel ini, kita akan membahas beberapa contoh soal matriks dan jawabannya.
Penjumlahan Matriks
Penjumlahan matriks adalah operasi penjumlahan elemen-elemen yang bersesuaian dari dua matriks dengan ukuran yang sama.
Contoh:
“`
A = [1 2]
[3 4]
B = [5 6]
[7 8]
A + B = [1+5 2+6]
[3+7 4+8]
= [6 8]
[10 12]
“`
Perkalian Matriks
Perkalian matriks adalah operasi perkalian elemen-elemen dari dua matriks dengan aturan tertentu.
Contoh:
“`
A = [1 2]
[3 4]
B = [5 6]
[7 8]
A x B = [1*5+2*7 1*6+2*8]
[3*5+4*7 3*6+4*8]
= [19 22]
[43 50]
“`
Determinan Matriks
Determinan matriks adalah nilai skalar yang dapat dihitung dari matriks persegi. Determinan matriks dapat digunakan untuk menyelesaikan sistem persamaan linear, menghitung luas segitiga, dan lain sebagainya.
Contoh:
“`
A = [2 3]
[4 5]
Det(A) = 2*5 – 3*4
= 10 – 12
= -2
“`
Tips Mengerjakan Soal Matriks
Matriks merupakan salah satu konsep penting dalam matematika yang memiliki banyak aplikasi dalam berbagai bidang, seperti fisika, ekonomi, dan ilmu komputer. Untuk menguasai materi ini, kamu perlu memahami konsep dasar matriks dan bagaimana menyelesaikan berbagai jenis soal yang berhubungan dengannya. Artikel ini akan membahas beberapa tips yang dapat membantu kamu dalam memahami konsep matriks dan menyelesaikan soal-soal matriks dengan cepat dan tepat.
Memahami Konsep Matriks
Sebelum kamu mulai mengerjakan soal matriks, pastikan kamu memahami konsep dasar matriks dengan baik. Hal ini akan membantu kamu dalam menyelesaikan soal-soal dengan lebih mudah dan cepat. Berikut beberapa tips untuk memahami konsep matriks:
- Pahami definisi matriks. Matriks adalah susunan bilangan yang disusun dalam baris dan kolom. Setiap bilangan dalam matriks disebut elemen matriks.
- Pelajari jenis-jenis matriks. Ada berbagai jenis matriks, seperti matriks persegi, matriks identitas, matriks nol, dan matriks transpose. Ketahui karakteristik dari masing-masing jenis matriks.
- Pahami operasi matriks. Operasi matriks meliputi penjumlahan, pengurangan, perkalian, dan determinan. Pastikan kamu memahami cara melakukan operasi-operasi tersebut dengan benar.
- Latih dengan contoh soal. Kerjakan contoh soal yang diberikan di buku teks atau di internet. Hal ini akan membantu kamu memahami konsep matriks dan melatih kemampuanmu dalam menyelesaikan soal.
Strategi Menyelesaikan Soal Matriks
Setelah memahami konsep dasar matriks, kamu dapat mempelajari strategi untuk menyelesaikan soal matriks dengan cepat dan tepat. Berikut beberapa tips yang dapat membantu kamu:
- Baca soal dengan cermat. Pastikan kamu memahami apa yang diminta dalam soal.
- Tentukan operasi matriks yang diperlukan. Identifikasi operasi matriks yang perlu dilakukan untuk menyelesaikan soal, seperti penjumlahan, pengurangan, perkalian, atau determinan.
- Selesaikan operasi matriks dengan benar. Gunakan rumus dan aturan yang benar untuk menyelesaikan operasi matriks.
- Periksa kembali jawaban. Setelah menyelesaikan soal, periksa kembali jawabanmu untuk memastikan bahwa jawabanmu benar.
Langkah Sistematis dalam Mengerjakan Soal Matriks
Berikut adalah langkah-langkah sistematis yang dapat kamu ikuti untuk menyelesaikan soal matriks:
- Pahami soal. Baca soal dengan cermat dan pastikan kamu memahami apa yang diminta.
- Tuliskan informasi yang diberikan. Catat semua informasi yang diberikan dalam soal, seperti matriks yang terlibat, operasi yang diminta, dan hasil yang diharapkan.
- Selesaikan operasi matriks. Gunakan rumus dan aturan yang benar untuk menyelesaikan operasi matriks yang diperlukan.
- Tuliskan jawaban. Tuliskan jawabanmu dengan jelas dan rapi.
- Periksa kembali jawaban. Pastikan jawabanmu benar dan sesuai dengan apa yang diminta dalam soal.
Referensi Pembelajaran Matriks
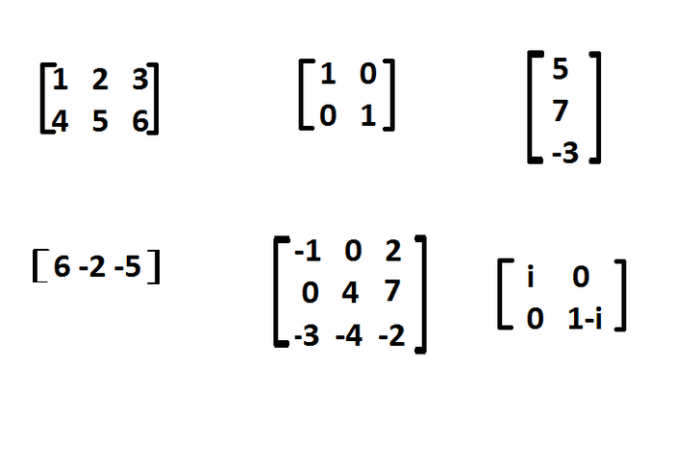
Materi matriks merupakan bagian penting dalam aljabar linear yang memiliki banyak aplikasi dalam berbagai bidang, seperti ilmu komputer, fisika, ekonomi, dan teknik. Untuk mempelajari matriks dengan lebih mendalam, Anda dapat memanfaatkan berbagai sumber belajar yang tersedia. Berikut adalah beberapa rekomendasi buku teks, website, dan video tutorial yang dapat membantu Anda dalam memahami konsep matriks.
Buku Teks Matematika tentang Matriks
Buku teks matematika tentang matriks memberikan penjelasan yang komprehensif dan sistematis mengenai konsep matriks, mulai dari definisi dasar hingga aplikasi dalam berbagai bidang. Berikut adalah beberapa buku teks yang direkomendasikan:
- Linear Algebra and Its Applications oleh David C. Lay: Buku ini dikenal karena penjelasannya yang jelas dan contoh-contohnya yang mudah dipahami. Buku ini juga membahas berbagai aplikasi matriks dalam bidang sains dan teknik.
- Introduction to Linear Algebra oleh Gilbert Strang: Buku ini membahas aljabar linear secara menyeluruh, dengan penekanan pada konsep-konsep kunci seperti ruang vektor, transformasi linear, dan nilai eigen. Buku ini juga dilengkapi dengan banyak contoh dan latihan.
- Elementary Linear Algebra oleh Howard Anton dan Chris Rorres: Buku ini merupakan pilihan yang baik untuk mempelajari dasar-dasar aljabar linear, termasuk konsep matriks, sistem persamaan linear, dan ruang vektor. Buku ini juga menyediakan banyak latihan dan solusi untuk membantu Anda memahami materi.
Website dan Platform Pembelajaran Online tentang Matriks
Website dan platform pembelajaran online menawarkan cara yang fleksibel dan interaktif untuk mempelajari matriks. Anda dapat mengakses materi pembelajaran, mengikuti kuis, dan berinteraksi dengan tutor online. Berikut adalah beberapa website dan platform yang direkomendasikan:
- Khan Academy: Platform ini menyediakan materi pembelajaran gratis tentang aljabar linear, termasuk topik tentang matriks, dengan video tutorial, latihan, dan kuis interaktif. Anda dapat belajar dengan kecepatan Anda sendiri dan mengakses materi yang Anda butuhkan.
- Coursera: Platform ini menawarkan berbagai kursus online tentang aljabar linear, termasuk kursus yang membahas konsep matriks secara mendalam. Anda dapat belajar dari profesor terkemuka di berbagai universitas ternama di dunia.
- MIT OpenCourseware: Website ini menyediakan akses gratis ke materi pembelajaran dari berbagai mata kuliah di MIT, termasuk aljabar linear. Anda dapat mengunduh catatan kuliah, video tutorial, dan tugas-tugas yang diberikan dalam mata kuliah tersebut.
Video Tutorial tentang Matriks
Video tutorial merupakan cara yang efektif untuk mempelajari matriks dengan visualisasi dan penjelasan yang mudah dipahami. Berikut adalah beberapa video tutorial yang direkomendasikan:
- 3Blue1Brown: Saluran YouTube ini menawarkan video tutorial yang kreatif dan menarik tentang berbagai topik matematika, termasuk aljabar linear dan matriks. Video-video ini menggunakan animasi dan visualisasi untuk menjelaskan konsep-konsep yang kompleks dengan cara yang mudah dipahami.
- Khan Academy: Platform ini juga menyediakan video tutorial tentang aljabar linear, termasuk topik tentang matriks, dengan penjelasan yang jelas dan mudah dipahami. Video-video ini cocok untuk pemula yang baru mempelajari konsep matriks.
- Professor Leonard: Saluran YouTube ini menyediakan video tutorial tentang berbagai topik matematika, termasuk aljabar linear dan matriks. Video-video ini membahas konsep-konsep secara detail dan disertai dengan contoh-contoh yang mudah dipahami.
Akhir Kata
Dengan memahami konsep matriks dan berlatih dengan contoh soal, Anda akan mampu menyelesaikan berbagai masalah yang melibatkan matriks dengan lebih mudah dan percaya diri. Matriks bukan hanya sekumpulan angka, tetapi alat yang powerful untuk memecahkan masalah kompleks di berbagai bidang. Jadi, jangan ragu untuk terus belajar dan berlatih agar Anda dapat menguasai konsep matriks dengan baik.




