Contoh soal mean data berkelompok – Pernahkah Anda menemukan data yang dikelompokkan dalam rentang tertentu, seperti nilai ujian siswa yang dibagi menjadi beberapa kelas? Jika ya, maka Anda perlu memahami cara menghitung rata-rata data berkelompok, yang dikenal sebagai mean data berkelompok. Menghitung mean data berkelompok memiliki keunikan tersendiri, karena data yang kita hadapi bukan lagi data tunggal, melainkan data yang terkelompokkan dalam rentang tertentu.
Dalam artikel ini, kita akan membahas langkah-langkah menghitung mean data berkelompok, menjelajahi contoh soal yang menarik, dan mengungkap manfaatnya dalam berbagai situasi. Siap untuk mempelajari cara menghitung mean data berkelompok? Mari kita mulai!
Pengertian Mean Data Berkelompok
Dalam dunia statistik, mean data berkelompok adalah nilai rata-rata dari suatu kumpulan data yang telah dikelompokkan ke dalam kelas-kelas tertentu. Data berkelompok biasanya digunakan ketika kita memiliki data yang banyak dan beragam, sehingga lebih mudah untuk menganalisisnya dengan mengelompokkannya berdasarkan rentang nilai tertentu.
Contoh Data Berkelompok dan Cara Menghitung Mean
Misalnya, kita ingin mengetahui rata-rata nilai ujian matematika dari 50 siswa. Alih-alih menuliskan nilai setiap siswa secara terpisah, kita bisa mengelompokkannya ke dalam kelas-kelas nilai, seperti 0-10, 11-20, 21-30, dan seterusnya. Setiap kelas memiliki frekuensi, yaitu jumlah siswa yang mendapat nilai dalam rentang kelas tersebut.
Untuk menghitung mean data berkelompok, kita perlu mengetahui nilai tengah setiap kelas dan frekuensi kelas tersebut. Nilai tengah kelas adalah rata-rata dari batas bawah dan batas atas kelas. Setelah kita mendapatkan nilai tengah dan frekuensi setiap kelas, kita dapat menghitung mean data berkelompok dengan rumus berikut:
Mean data berkelompok = (Σ(nilai tengah kelas * frekuensi kelas)) / Σ(frekuensi kelas)
Sebagai contoh, perhatikan tabel berikut yang menunjukkan data nilai ujian matematika 50 siswa:
| Kelas Nilai | Nilai Tengah (xi) | Frekuensi (fi) | xi * fi |
|---|---|---|---|
| 0-10 | 5 | 5 | 25 |
| 11-20 | 15.5 | 10 | 155 |
| 21-30 | 25.5 | 15 | 382.5 |
| 31-40 | 35.5 | 10 | 355 |
| 41-50 | 45.5 | 10 | 455 |
Berdasarkan tabel tersebut, kita dapat menghitung mean data berkelompok sebagai berikut:
Mean data berkelompok = (25 + 155 + 382.5 + 355 + 455) / (5 + 10 + 15 + 10 + 10) = 27.25
Jadi, rata-rata nilai ujian matematika dari 50 siswa adalah 27.25.
Perbedaan Mean Data Tunggal dan Mean Data Berkelompok
Mean data tunggal dan mean data berkelompok memiliki perbedaan utama dalam cara perhitungannya. Mean data tunggal dihitung dengan menjumlahkan semua nilai data dan membaginya dengan jumlah data. Sedangkan mean data berkelompok dihitung dengan menggunakan nilai tengah kelas dan frekuensi kelas.
- Mean data tunggal digunakan ketika kita memiliki data yang tidak dikelompokkan dan nilai setiap data diketahui.
- Mean data berkelompok digunakan ketika kita memiliki data yang dikelompokkan ke dalam kelas-kelas tertentu dan nilai setiap data tidak diketahui.
Berikut adalah tabel yang menunjukkan perbedaan antara mean data tunggal dan mean data berkelompok:
| Aspek | Mean Data Tunggal | Mean Data Berkelompok |
|---|---|---|
| Data | Tidak dikelompokkan | Dikelompokkan |
| Perhitungan | Σ(nilai data) / jumlah data | (Σ(nilai tengah kelas * frekuensi kelas)) / Σ(frekuensi kelas) |
| Kegunaan | Untuk data yang tidak dikelompokkan | Untuk data yang dikelompokkan |
Rumus Mean Data Berkelompok
Mean data berkelompok merupakan nilai rata-rata dari data yang telah dikelompokkan ke dalam kelas-kelas interval. Rumus mean data berkelompok digunakan untuk menghitung nilai rata-rata data yang terdistribusi dalam interval-interval tertentu, bukan data tunggal. Rumus ini mempertimbangkan frekuensi setiap kelas interval, sehingga memberikan gambaran yang lebih akurat tentang nilai rata-rata data.
Rumus Mean Data Berkelompok
Rumus mean data berkelompok adalah:
Mean = (∑(fi * xi)) / ∑fi
Keterangan:
- Mean: Nilai rata-rata data berkelompok
- fi: Frekuensi kelas ke-i
- xi: Titik tengah kelas ke-i
- ∑: Simbol penjumlahan
Langkah-langkah Menghitung Mean Data Berkelompok
Berikut langkah-langkah menghitung mean data berkelompok:
- Tentukan titik tengah (xi) dari setiap kelas interval.
- Kalikan titik tengah setiap kelas interval dengan frekuensinya (fi * xi).
- Jumlahkan hasil perkalian dari langkah 2 (∑(fi * xi)).
- Jumlahkan semua frekuensi (∑fi).
- Bagi hasil penjumlahan dari langkah 3 dengan hasil penjumlahan dari langkah 4. Hasilnya adalah mean data berkelompok.
Contoh Soal dan Penyelesaian
Misalnya, kita memiliki data nilai ujian matematika dari 50 siswa yang dikelompokkan dalam tabel berikut:
| Kelas Interval | Frekuensi (fi) |
|---|---|
| 51 – 60 | 5 |
| 61 – 70 | 10 |
| 71 – 80 | 15 |
| 81 – 90 | 12 |
| 91 – 100 | 8 |
Langkah-langkah menghitung mean data berkelompok:
- Tentukan titik tengah (xi) dari setiap kelas interval:
- Kalikan titik tengah setiap kelas interval dengan frekuensinya (fi * xi):
- Jumlahkan hasil perkalian dari langkah 2 (∑(fi * xi)) = 277.5 + 655 + 1132.5 + 1026 + 764 = 3855
- Jumlahkan semua frekuensi (∑fi) = 5 + 10 + 15 + 12 + 8 = 50
- Bagi hasil penjumlahan dari langkah 3 dengan hasil penjumlahan dari langkah 4: Mean = 3855 / 50 = 77.1
| Kelas Interval | Frekuensi (fi) | Titik Tengah (xi) |
|---|---|---|
| 51 – 60 | 5 | 55.5 |
| 61 – 70 | 10 | 65.5 |
| 71 – 80 | 15 | 75.5 |
| 81 – 90 | 12 | 85.5 |
| 91 – 100 | 8 | 95.5 |
| Kelas Interval | Frekuensi (fi) | Titik Tengah (xi) | fi * xi |
|---|---|---|---|
| 51 – 60 | 5 | 55.5 | 277.5 |
| 61 – 70 | 10 | 65.5 | 655 |
| 71 – 80 | 15 | 75.5 | 1132.5 |
| 81 – 90 | 12 | 85.5 | 1026 |
| 91 – 100 | 8 | 95.5 | 764 |
Jadi, mean data berkelompok nilai ujian matematika dari 50 siswa adalah 77.1.
Contoh Soal Mean Data Berkelompok
Menghitung mean data berkelompok merupakan cara untuk menemukan nilai tengah dari data yang telah dikelompokkan ke dalam kelas-kelas interval. Metode ini berguna untuk data yang memiliki banyak nilai, sehingga lebih mudah dikelompokkan dan dianalisis. Dalam artikel ini, kita akan mempelajari contoh soal mean data berkelompok dengan tingkat kesulitan yang berbeda.
Contoh Soal Mean Data Berkelompok Tingkat Kesulitan Rendah
Contoh soal pertama ini akan menunjukkan bagaimana menghitung mean data berkelompok untuk data yang sederhana dan memiliki jumlah kelas interval yang sedikit.
| Kelas Interval | Frekuensi (f) |
|---|---|
| 10 – 14 | 5 |
| 15 – 19 | 8 |
| 20 – 24 | 7 |
Langkah-langkah untuk menghitung mean data berkelompok adalah:
- Tentukan titik tengah (xi) dari setiap kelas interval. Titik tengah dihitung dengan rumus:
- Kalikan titik tengah (xi) dengan frekuensi (f) masing-masing kelas interval untuk mendapatkan nilai f * xi.
- Jumlahkan semua nilai f * xi.
- Jumlahkan semua frekuensi (f).
- Hitung mean data berkelompok dengan rumus:
xi = (batas atas kelas + batas bawah kelas) / 2
Mean = Σ(f * xi) / Σf
Berikut perhitungan mean data berkelompok untuk contoh soal pertama:
| Kelas Interval | Frekuensi (f) | Titik Tengah (xi) | f * xi |
|---|---|---|---|
| 10 – 14 | 5 | 12 | 60 |
| 15 – 19 | 8 | 17 | 136 |
| 20 – 24 | 7 | 22 | 154 |
| Total | 20 | 350 |
Mean data berkelompok = Σ(f * xi) / Σf = 350 / 20 = 17.5
Contoh Soal Mean Data Berkelompok Tingkat Kesulitan Sedang
Contoh soal kedua ini akan menunjukkan bagaimana menghitung mean data berkelompok untuk data yang memiliki jumlah kelas interval lebih banyak dan rentang data yang lebih besar.
| Kelas Interval | Frekuensi (f) |
|---|---|
| 50 – 59 | 3 |
| 60 – 69 | 7 |
| 70 – 79 | 12 |
| 80 – 89 | 10 |
| 90 – 99 | 8 |
Langkah-langkah untuk menghitung mean data berkelompok sama dengan contoh soal pertama. Berikut perhitungan mean data berkelompok untuk contoh soal kedua:
| Kelas Interval | Frekuensi (f) | Titik Tengah (xi) | f * xi |
|---|---|---|---|
| 50 – 59 | 3 | 54.5 | 163.5 |
| 60 – 69 | 7 | 64.5 | 451.5 |
| 70 – 79 | 12 | 74.5 | 894 |
| 80 – 89 | 10 | 84.5 | 845 |
| 90 – 99 | 8 | 94.5 | 756 |
| Total | 40 | 3110 |
Mean data berkelompok = Σ(f * xi) / Σf = 3110 / 40 = 77.75
Contoh Soal Mean Data Berkelompok Tingkat Kesulitan Tinggi
Contoh soal ketiga ini akan menunjukkan bagaimana menghitung mean data berkelompok untuk data yang memiliki jumlah kelas interval yang lebih banyak dan rentang data yang lebih besar, serta melibatkan perhitungan yang lebih kompleks.
| Kelas Interval | Frekuensi (f) |
|---|---|
| 100 – 149 | 5 |
| 150 – 199 | 10 |
| 200 – 249 | 15 |
| 250 – 299 | 20 |
| 300 – 349 | 12 |
| 350 – 399 | 8 |
Langkah-langkah untuk menghitung mean data berkelompok sama dengan contoh soal sebelumnya. Berikut perhitungan mean data berkelompok untuk contoh soal ketiga:
| Kelas Interval | Frekuensi (f) | Titik Tengah (xi) | f * xi |
|---|---|---|---|
| 100 – 149 | 5 | 124.5 | 622.5 |
| 150 – 199 | 10 | 174.5 | 1745 |
| 200 – 249 | 15 | 224.5 | 3367.5 |
| 250 – 299 | 20 | 274.5 | 5490 |
| 300 – 349 | 12 | 324.5 | 3894 |
| 350 – 399 | 8 | 374.5 | 2996 |
| Total | 70 | 17115 |
Mean data berkelompok = Σ(f * xi) / Σf = 17115 / 70 = 244.5
Penerapan Mean Data Berkelompok
Mean data berkelompok adalah nilai rata-rata dari data yang telah dikelompokkan dalam kelas-kelas tertentu. Penerapannya sangat luas, mulai dari analisis data statistik dalam berbagai bidang, seperti ekonomi, sosial, pendidikan, hingga dalam kehidupan sehari-hari.
Contoh Penerapan Mean Data Berkelompok
Berikut adalah beberapa contoh penerapan mean data berkelompok dalam kehidupan sehari-hari:
- Analisis Data Penjualan Produk: Seorang manajer toko ingin mengetahui rata-rata penjualan produk tertentu dalam satu bulan. Ia mengelompokkan data penjualan berdasarkan kategori produk, seperti makanan, minuman, dan pakaian. Dengan menghitung mean data berkelompok, manajer dapat mengetahui produk mana yang paling laris dan mengidentifikasi tren penjualan.
- Menghitung Rata-rata Usia Siswa di Sekolah: Guru ingin mengetahui rata-rata usia siswa di kelasnya. Ia mengelompokkan siswa berdasarkan rentang usia, misalnya 7-8 tahun, 9-10 tahun, dan 11-12 tahun. Dengan menghitung mean data berkelompok, guru dapat memperoleh informasi tentang distribusi usia siswa di kelas.
- Analisis Data Kepuasan Pelanggan: Sebuah perusahaan ingin mengetahui tingkat kepuasan pelanggan terhadap layanannya. Mereka mengelompokkan data berdasarkan skor kepuasan pelanggan, misalnya 1-3, 4-6, dan 7-9. Dengan menghitung mean data berkelompok, perusahaan dapat mengetahui skor kepuasan pelanggan secara keseluruhan dan mengidentifikasi area yang perlu ditingkatkan.
Manfaat Menghitung Mean Data Berkelompok
Menghitung mean data berkelompok memiliki beberapa manfaat, antara lain:
- Memberikan gambaran umum tentang data: Mean data berkelompok dapat memberikan informasi tentang nilai rata-rata data secara keseluruhan, sehingga memudahkan untuk memahami distribusi data.
- Memudahkan analisis data: Data berkelompok lebih mudah dianalisis dibandingkan dengan data mentah, karena data telah dikelompokkan berdasarkan kelas-kelas tertentu.
- Meningkatkan akurasi: Mean data berkelompok dapat memberikan hasil yang lebih akurat dibandingkan dengan mean data mentah, terutama jika data memiliki banyak outlier.
Kelebihan dan Kekurangan Mean Data Berkelompok: Contoh Soal Mean Data Berkelompok
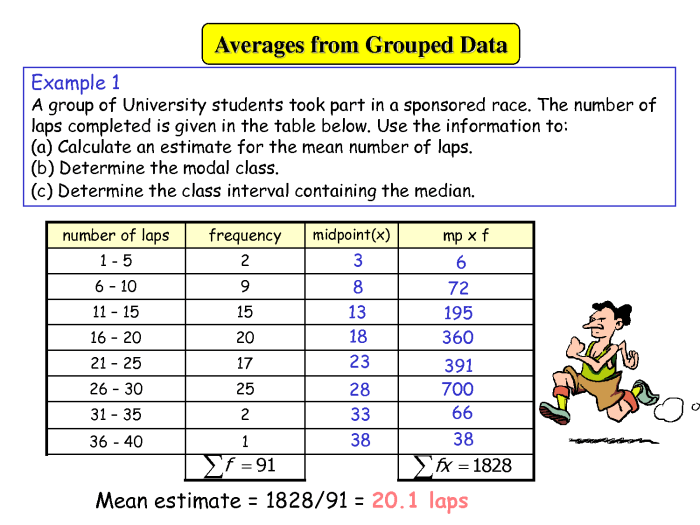
Mean data berkelompok adalah ukuran tendensi sentral yang digunakan untuk menghitung nilai rata-rata dari data yang telah dikelompokkan dalam interval kelas. Metode ini sangat berguna untuk data yang memiliki banyak nilai yang berbeda dan sulit untuk dihitung satu per satu. Meskipun memiliki keunggulan, mean data berkelompok juga memiliki beberapa kelemahan. Berikut adalah penjelasan lebih lanjut mengenai kelebihan dan kekurangan mean data berkelompok dibandingkan dengan mean data tunggal.
Kelebihan Mean Data Berkelompok
Mean data berkelompok memiliki beberapa kelebihan dibandingkan dengan mean data tunggal, terutama dalam hal efisiensi dan representasi data.
- Efisiensi dalam Menghitung Nilai Rata-rata: Mean data berkelompok memungkinkan kita untuk menghitung nilai rata-rata dari kumpulan data yang besar dengan lebih efisien. Kita tidak perlu menghitung setiap nilai data satu per satu, melainkan cukup menghitung nilai tengah dari setiap interval kelas dan mengalikannya dengan frekuensi kelas tersebut. Hal ini sangat membantu dalam menghemat waktu dan tenaga, terutama jika data yang dihadapi sangat banyak.
- Representasi Data yang Lebih Baik: Mean data berkelompok dapat memberikan gambaran yang lebih baik tentang distribusi data. Dengan mengelompokkan data ke dalam interval kelas, kita dapat melihat pola dan tren dalam data dengan lebih jelas. Hal ini dapat membantu kita dalam memahami karakteristik data secara keseluruhan.
- Mempermudah Analisis Data: Mean data berkelompok juga mempermudah analisis data. Dengan mengelompokkan data, kita dapat membandingkan nilai rata-rata antar kelompok dan melihat perbedaan yang signifikan. Hal ini sangat berguna dalam analisis statistik dan pengambilan keputusan.
Kekurangan Mean Data Berkelompok
Meskipun memiliki banyak kelebihan, mean data berkelompok juga memiliki beberapa kekurangan yang perlu diperhatikan.
- Kehilangan Informasi Detail: Salah satu kelemahan utama mean data berkelompok adalah kehilangan informasi detail. Ketika kita mengelompokkan data, kita mengabaikan nilai data individual dalam setiap interval kelas. Hal ini dapat menyebabkan hilangnya informasi penting yang mungkin tidak terlihat dalam data yang telah dikelompokkan.
- Rentan Terhadap Kesalahan Pembulatan: Mean data berkelompok dapat dipengaruhi oleh kesalahan pembulatan. Dalam menghitung nilai tengah setiap interval kelas, kita mungkin melakukan pembulatan. Kesalahan pembulatan ini dapat memengaruhi akurasi nilai rata-rata yang dihitung.
- Tidak Sesuai untuk Data dengan Variasi Kecil: Mean data berkelompok tidak efektif untuk data dengan variasi kecil. Dalam kasus ini, mean data tunggal mungkin lebih tepat digunakan karena tidak akan kehilangan informasi detail yang penting.
Contoh Situasi di Mana Mean Data Berkelompok Lebih Efektif Digunakan
Mean data berkelompok sangat efektif digunakan dalam situasi di mana data memiliki banyak nilai yang berbeda dan sulit untuk dihitung satu per satu. Misalnya, dalam penelitian tentang pendapatan penduduk suatu daerah, kita mungkin menemukan banyak nilai pendapatan yang berbeda. Dalam kasus ini, mean data berkelompok dapat digunakan untuk menghitung nilai rata-rata pendapatan dengan mengelompokkan data ke dalam interval kelas, seperti “Rp 1-2 juta”, “Rp 2-3 juta”, dan seterusnya. Hal ini akan membantu kita untuk memahami distribusi pendapatan penduduk secara keseluruhan dan membuat analisis yang lebih mudah.
Perbedaan Mean, Median, dan Modus Data Berkelompok
Dalam statistika, data berkelompok merupakan data yang disusun dalam kelas interval. Data berkelompok sering digunakan untuk menyederhanakan data yang banyak dan memudahkan analisis. Untuk menganalisis data berkelompok, kita dapat menggunakan ukuran pemusatan data, yaitu mean, median, dan modus. Ketiga ukuran ini memiliki konsep dan cara perhitungan yang berbeda, sehingga menghasilkan nilai yang berbeda pula.
Perbedaan Mean, Median, dan Modus Data Berkelompok
Berikut tabel yang membandingkan mean, median, dan modus data berkelompok:
| Ukuran Pemusatan Data | Konsep | Cara Perhitungan |
|---|---|---|
| Mean | Nilai rata-rata dari semua data dalam kelompok |
Menghitung jumlah data dalam setiap kelas interval, mengalikannya dengan titik tengah kelas, menjumlahkan hasil perkalian tersebut, dan membagi dengan jumlah total data. Rumus:
Keterangan:
|
| Median | Nilai tengah dari data yang telah diurutkan |
Menentukan kelas median, yaitu kelas interval yang memuat data ke-(n/2), kemudian menghitung nilai median dengan rumus:
Keterangan:
|
| Modus | Nilai yang paling sering muncul dalam data |
Menentukan kelas modus, yaitu kelas interval dengan frekuensi tertinggi, kemudian menghitung nilai modus dengan rumus:
Keterangan:
|
Contoh Perhitungan Mean, Median, dan Modus Data Berkelompok
Misalnya, kita memiliki data berkelompok tentang tinggi badan siswa dalam suatu kelas, seperti berikut:
| Tinggi Badan (cm) | Frekuensi |
|---|---|
| 150 – 155 | 5 |
| 155 – 160 | 10 |
| 160 – 165 | 15 |
| 165 – 170 | 8 |
| 170 – 175 | 2 |
Berdasarkan data tersebut, kita dapat menghitung mean, median, dan modus:
Mean
Untuk menghitung mean, kita perlu menentukan titik tengah setiap kelas interval. Misalnya, titik tengah kelas interval 150 – 155 adalah (150 + 155) / 2 = 152,5. Kemudian, kita kalikan titik tengah setiap kelas dengan frekuensinya, menjumlahkan hasil perkalian tersebut, dan membagi dengan jumlah total data.
Berikut perhitungan mean:
| Tinggi Badan (cm) | Frekuensi (fi) | Titik Tengah (xi) | fi * xi |
|---|---|---|---|
| 150 – 155 | 5 | 152,5 | 762,5 |
| 155 – 160 | 10 | 157,5 | 1575 |
| 160 – 165 | 15 | 162,5 | 2437,5 |
| 165 – 170 | 8 | 167,5 | 1340 |
| 170 – 175 | 2 | 172,5 | 345 |
| Total | 40 | 6460 |
Mean = ∑(fi * xi) / ∑fi = 6460 / 40 = 161,5 cm
Median
Untuk menghitung median, kita perlu menentukan kelas median. Jumlah total data (n) adalah 40, sehingga data ke-(n/2) adalah data ke-20. Kelas median adalah kelas interval 160 – 165 karena memuat data ke-20.
Berikut perhitungan median:
L = 160 (batas bawah kelas median)
n = 40 (jumlah total data)
Fkb = 15 (frekuensi kumulatif sebelum kelas median)
fk = 15 (frekuensi kelas median)
p = 5 (panjang kelas interval)
Contoh soal mean data berkelompok memang terkadang terasa rumit, tapi sebenarnya cukup mudah dipahami. Kamu perlu ingat cara menghitung mean data berkelompok dan bagaimana menggunakan rumus yang tepat. Ingat, menghitung mean data berkelompok mirip dengan menghitung rata-rata, hanya saja data dikelompokkan dalam interval tertentu.
Misalnya, jika kamu sedang mempelajari fisika, kamu mungkin akan menemukan contoh soal mean data berkelompok dalam menghitung kecepatan rata-rata suatu benda yang bergerak secara vertikal ke bawah. Kamu bisa menemukan contoh soal gerak vertikal ke bawah di sini.
Nah, setelah memahami konsep gerak vertikal ke bawah, kamu bisa menerapkannya pada soal mean data berkelompok. Ingat, kunci dalam memahami soal mean data berkelompok adalah memahami konsep dasar dan latihan secara rutin.
Median = L + ((n/2 – Fkb) / fk) * p = 160 + ((40/2 – 15) / 15) * 5 = 161,67 cm
Modus
Untuk menghitung modus, kita perlu menentukan kelas modus. Kelas modus adalah kelas interval 160 – 165 karena memiliki frekuensi tertinggi, yaitu 15.
Berikut perhitungan modus:
L = 160 (batas bawah kelas modus)
d1 = 15 – 10 = 5 (selisih frekuensi kelas modus dengan kelas sebelumnya)
d2 = 15 – 8 = 7 (selisih frekuensi kelas modus dengan kelas sesudahnya)
p = 5 (panjang kelas interval)
Modus = L + ((d1 / (d1 + d2)) * p) = 160 + ((5 / (5 + 7)) * 5) = 161,54 cm
Dari contoh di atas, dapat dilihat bahwa nilai mean, median, dan modus data berkelompok berbeda. Mean menunjukkan nilai rata-rata dari semua data, median menunjukkan nilai tengah dari data yang telah diurutkan, dan modus menunjukkan nilai yang paling sering muncul dalam data.
Pengaruh Data Ekstrem terhadap Mean Data Berkelompok
Mean data berkelompok, yang juga dikenal sebagai rata-rata data berkelompok, merupakan nilai tengah dari kumpulan data yang telah dikelompokkan ke dalam kelas-kelas tertentu. Dalam menghitung mean data berkelompok, kita menggunakan titik tengah setiap kelas dan frekuensi kelas tersebut. Namun, keberadaan data ekstrem dalam data berkelompok dapat memengaruhi nilai mean secara signifikan.
Pengaruh Data Ekstrem terhadap Mean Data Berkelompok
Data ekstrem, yang merupakan nilai yang jauh lebih tinggi atau lebih rendah dibandingkan dengan data lainnya dalam suatu kelompok, dapat menyebabkan mean data berkelompok menjadi bias. Hal ini karena mean merupakan nilai yang sensitif terhadap nilai-nilai ekstrem.
Contoh Data Berkelompok dengan Data Ekstrem
Misalkan kita memiliki data tentang tinggi badan siswa dalam suatu kelas yang dibagi menjadi beberapa kelas interval. Berikut adalah contoh data berkelompok dengan data ekstrem:
| Kelas Interval (cm) | Frekuensi |
|---|---|
| 140 – 145 | 5 |
| 145 – 150 | 10 |
| 150 – 155 | 15 |
| 155 – 160 | 20 |
| 160 – 165 | 10 |
| 165 – 170 | 5 |
| 170 – 175 | 1 |
Dalam contoh data di atas, terlihat bahwa terdapat satu siswa dengan tinggi badan 172 cm, yang termasuk dalam kelas interval 170 – 175 cm. Data ini dapat dianggap sebagai data ekstrem karena jauh lebih tinggi dibandingkan dengan data lainnya.
Dampak Data Ekstrem terhadap Interpretasi Mean
Keberadaan data ekstrem dalam data berkelompok dapat memengaruhi interpretasi mean data tersebut. Mean data berkelompok yang terpengaruh oleh data ekstrem mungkin tidak mencerminkan nilai tengah yang sebenarnya dari data tersebut. Hal ini dapat menyebabkan kesimpulan yang salah tentang distribusi data.
- Misalnya, jika kita menghitung mean dari data tinggi badan siswa di atas tanpa mempertimbangkan data ekstrem, maka mean akan terpengaruh dan tidak akan mencerminkan nilai tengah yang sebenarnya dari tinggi badan siswa dalam kelas tersebut.
- Dalam situasi ini, penggunaan mean mungkin tidak tepat untuk menggambarkan distribusi data, dan kita mungkin perlu mempertimbangkan penggunaan ukuran tendensi sentral lainnya seperti median atau modus.
Interpretasi Mean Data Berkelompok
Setelah menghitung mean data berkelompok, langkah selanjutnya adalah menginterpretasikan hasilnya. Interpretasi ini akan membantu kita memahami makna dari nilai mean yang diperoleh dan bagaimana nilai tersebut dapat digunakan untuk analisis lebih lanjut.
Cara Menginterpretasikan Mean Data Berkelompok
Interpretasi mean data berkelompok melibatkan pemahaman tentang:
- Nilai Mean: Nilai mean menunjukkan titik tengah atau rata-rata dari data yang dikelompokkan. Ini memberi kita gambaran umum tentang lokasi pusat data.
- Rentang Data: Rentang data, yang diwakili oleh rentang kelas, menunjukkan seberapa tersebarnya data. Rentang yang luas menunjukkan variasi data yang tinggi, sedangkan rentang yang sempit menunjukkan variasi data yang rendah.
- Frekuensi: Frekuensi setiap kelas menunjukkan berapa banyak data yang berada dalam rentang kelas tertentu. Frekuensi tinggi menunjukkan bahwa lebih banyak data berada di kelas tersebut.
Contoh Interpretasi Mean Data Berkelompok
Misalnya, kita menghitung mean data berkelompok untuk nilai ujian matematika dari 50 siswa. Hasil perhitungan menunjukkan bahwa mean nilai ujian adalah 75. Kita juga melihat bahwa rentang kelas adalah 10 dan frekuensi tertinggi berada pada kelas 70-80. Berdasarkan informasi ini, kita dapat menginterpretasikan hasil sebagai berikut:
- Nilai Mean: Nilai rata-rata ujian matematika adalah 75, yang menunjukkan bahwa secara keseluruhan, siswa mencapai nilai yang cukup baik.
- Rentang Data: Rentang kelas 10 menunjukkan bahwa nilai ujian siswa bervariasi cukup besar, dengan beberapa siswa mencapai nilai yang sangat tinggi dan beberapa lainnya mencapai nilai yang lebih rendah.
- Frekuensi: Frekuensi tertinggi pada kelas 70-80 menunjukkan bahwa sebagian besar siswa mendapatkan nilai dalam rentang ini. Ini menunjukkan bahwa sebagian besar siswa memiliki pemahaman yang baik tentang materi ujian.
Manfaat Interpretasi Mean Data Berkelompok
Interpretasi mean data berkelompok dapat membantu dalam berbagai hal, seperti:
- Pengambilan Keputusan: Mean dapat digunakan untuk membandingkan kinerja kelompok yang berbeda atau untuk mengidentifikasi area yang perlu ditingkatkan.
- Analisis Data: Mean memberikan titik referensi untuk memahami distribusi data dan mengidentifikasi tren atau pola.
- Komunikasi: Mean merupakan cara yang mudah dan efektif untuk meringkas data dan mengkomunikasikan informasi penting kepada audiens yang lebih luas.
Aplikasi Mean Data Berkelompok dalam Statistik
Mean data berkelompok adalah ukuran tendensi sentral yang sangat berguna dalam statistik. Ini memungkinkan kita untuk menghitung nilai rata-rata dari kumpulan data yang besar, bahkan ketika data dikelompokkan dalam kelas-kelas interval. Mean data berkelompok memiliki banyak aplikasi praktis dalam berbagai bidang, mulai dari ilmu sosial hingga sains dan bisnis.
Aplikasi Mean Data Berkelompok dalam Berbagai Bidang
Mean data berkelompok digunakan dalam berbagai bidang, seperti:
- Ilmu Sosial: Mean data berkelompok dapat digunakan untuk menganalisis data demografis, seperti pendapatan, pendidikan, dan usia. Misalnya, kita dapat menghitung rata-rata pendapatan penduduk di suatu wilayah berdasarkan kelompok umur atau tingkat pendidikan.
- Sains: Mean data berkelompok digunakan untuk menganalisis data ilmiah, seperti suhu, tekanan, atau konsentrasi. Misalnya, seorang ahli biologi dapat menggunakan mean data berkelompok untuk menghitung rata-rata suhu air di danau selama periode waktu tertentu.
- Bisnis: Mean data berkelompok digunakan untuk menganalisis data bisnis, seperti penjualan, keuntungan, dan biaya. Misalnya, seorang manajer pemasaran dapat menggunakan mean data berkelompok untuk menghitung rata-rata penjualan produk tertentu selama periode waktu tertentu.
Contoh Penelitian atau Analisis Data yang Menggunakan Mean Data Berkelompok
Sebagai contoh, mari kita perhatikan penelitian tentang pengaruh tingkat pendidikan terhadap pendapatan. Data tentang pendapatan dan tingkat pendidikan dikumpulkan dari sampel populasi. Data tersebut kemudian dikelompokkan berdasarkan tingkat pendidikan, seperti SD, SMP, SMA, dan Perguruan Tinggi. Mean data berkelompok kemudian dihitung untuk setiap kelompok pendidikan. Hasilnya menunjukkan bahwa rata-rata pendapatan meningkat seiring dengan meningkatnya tingkat pendidikan.
Peran Mean Data Berkelompok dalam Penelitian atau Analisis Data
Mean data berkelompok berperan penting dalam penelitian dan analisis data dengan cara berikut:
- Menyederhanakan data yang kompleks: Mean data berkelompok menyederhanakan kumpulan data yang besar dengan mengelompokkan data ke dalam kelas-kelas interval. Hal ini memudahkan untuk melihat tren dan pola dalam data.
- Memudahkan perbandingan: Mean data berkelompok memungkinkan kita untuk membandingkan rata-rata dari berbagai kelompok data. Misalnya, kita dapat membandingkan rata-rata pendapatan orang yang berpendidikan tinggi dengan rata-rata pendapatan orang yang berpendidikan rendah.
- Menghasilkan kesimpulan yang lebih akurat: Dengan menggunakan mean data berkelompok, kita dapat memperoleh estimasi yang lebih akurat dari rata-rata populasi, terutama ketika data tidak tersedia untuk setiap individu dalam populasi.
Latihan Soal Mean Data Berkelompok
Menghitung mean data berkelompok merupakan salah satu cara untuk menentukan nilai rata-rata dari data yang dikelompokkan dalam kelas-kelas tertentu. Metode ini berguna ketika kita berhadapan dengan data yang banyak dan perlu dikelompokkan agar analisisnya lebih mudah. Dalam latihan soal berikut, kita akan menguji pemahamanmu tentang cara menghitung mean data berkelompok dengan berbagai tingkat kesulitan.
Soal 1: Data Tinggi Badan Siswa
Berikut adalah data tinggi badan siswa kelas VII di sebuah SMP:
| Tinggi Badan (cm) | Frekuensi |
|---|---|
| 140 – 145 | 5 |
| 145 – 150 | 10 |
| 150 – 155 | 15 |
| 155 – 160 | 8 |
| 160 – 165 | 2 |
Tentukan mean tinggi badan siswa kelas VII tersebut.
Kunci Jawaban dan Pembahasan Soal 1
Untuk menghitung mean data berkelompok, kita perlu menentukan titik tengah setiap kelas interval, kemudian mengalikannya dengan frekuensi kelas tersebut. Setelah itu, jumlahkan hasil perkalian tersebut dan bagi dengan jumlah frekuensi.
| Tinggi Badan (cm) | Frekuensi (f) | Titik Tengah (x) | f * x |
|---|---|---|---|
| 140 – 145 | 5 | 142,5 | 712,5 |
| 145 – 150 | 10 | 147,5 | 1475 |
| 150 – 155 | 15 | 152,5 | 2287,5 |
| 155 – 160 | 8 | 157,5 | 1260 |
| 160 – 165 | 2 | 162,5 | 325 |
| Total | 40 | 5060 |
Mean tinggi badan siswa kelas VII adalah:
Mean = Σ(f * x) / Σf = 5060 / 40 = 126,5 cm
Jadi, mean tinggi badan siswa kelas VII adalah 126,5 cm.
Soal 2: Data Usia Karyawan
Berikut adalah data usia karyawan di sebuah perusahaan:
| Usia (tahun) | Frekuensi |
|---|---|
| 20 – 25 | 12 |
| 25 – 30 | 18 |
| 30 – 35 | 15 |
| 35 – 40 | 10 |
| 40 – 45 | 5 |
Tentukan mean usia karyawan di perusahaan tersebut.
Kunci Jawaban dan Pembahasan Soal 2
Sama seperti soal sebelumnya, kita akan menentukan titik tengah setiap kelas interval, mengalikannya dengan frekuensi kelas tersebut, kemudian menjumlahkan hasil perkalian tersebut dan membaginya dengan jumlah frekuensi.
| Usia (tahun) | Frekuensi (f) | Titik Tengah (x) | f * x |
|---|---|---|---|
| 20 – 25 | 12 | 22,5 | 270 |
| 25 – 30 | 18 | 27,5 | 495 |
| 30 – 35 | 15 | 32,5 | 487,5 |
| 35 – 40 | 10 | 37,5 | 375 |
| 40 – 45 | 5 | 42,5 | 212,5 |
| Total | 60 | 1840 |
Mean usia karyawan di perusahaan tersebut adalah:
Mean = Σ(f * x) / Σf = 1840 / 60 = 30,67 tahun
Jadi, mean usia karyawan di perusahaan tersebut adalah 30,67 tahun.
Soal 3: Data Skor Ujian
Berikut adalah data skor ujian matematika siswa kelas VIII:
| Skor | Frekuensi |
|---|---|
| 60 – 65 | 3 |
| 65 – 70 | 7 |
| 70 – 75 | 12 |
| 75 – 80 | 10 |
| 80 – 85 | 5 |
Tentukan mean skor ujian matematika siswa kelas VIII tersebut.
Kunci Jawaban dan Pembahasan Soal 3, Contoh soal mean data berkelompok
Kita akan menggunakan metode yang sama seperti pada soal sebelumnya untuk menghitung mean skor ujian matematika siswa kelas VIII.
| Skor | Frekuensi (f) | Titik Tengah (x) | f * x |
|---|---|---|---|
| 60 – 65 | 3 | 62,5 | 187,5 |
| 65 – 70 | 7 | 67,5 | 472,5 |
| 70 – 75 | 12 | 72,5 | 870 |
| 75 – 80 | 10 | 77,5 | 775 |
| 80 – 85 | 5 | 82,5 | 412,5 |
| Total | 37 | 2717,5 |
Mean skor ujian matematika siswa kelas VIII adalah:
Mean = Σ(f * x) / Σf = 2717,5 / 37 = 73,45
Jadi, mean skor ujian matematika siswa kelas VIII adalah 73,45.
Soal 4: Data Jumlah Penjualan
Berikut adalah data jumlah penjualan produk A di sebuah toko selama 5 hari:
| Jumlah Penjualan | Frekuensi |
|---|---|
| 10 – 15 | 1 |
| 15 – 20 | 2 |
| 20 – 25 | 3 |
| 25 – 30 | 2 |
| 30 – 35 | 1 |
Tentukan mean jumlah penjualan produk A selama 5 hari tersebut.
Kunci Jawaban dan Pembahasan Soal 4
Kita akan menggunakan metode yang sama seperti pada soal sebelumnya untuk menghitung mean jumlah penjualan produk A selama 5 hari.
| Jumlah Penjualan | Frekuensi (f) | Titik Tengah (x) | f * x |
|---|---|---|---|
| 10 – 15 | 1 | 12,5 | 12,5 |
| 15 – 20 | 2 | 17,5 | 35 |
| 20 – 25 | 3 | 22,5 | 67,5 |
| 25 – 30 | 2 | 27,5 | 55 |
| 30 – 35 | 1 | 32,5 | 32,5 |
| Total | 9 | 202,5 |
Mean jumlah penjualan produk A selama 5 hari adalah:
Mean = Σ(f * x) / Σf = 202,5 / 9 = 22,5
Jadi, mean jumlah penjualan produk A selama 5 hari adalah 22,5.
Soal 5: Data Berat Badan Mahasiswa
Berikut adalah data berat badan mahasiswa di sebuah universitas:
| Berat Badan (kg) | Frekuensi |
|---|---|
| 45 – 50 | 10 |
| 50 – 55 | 15 |
| 55 – 60 | 20 |
| 60 – 65 | 12 |
| 65 – 70 | 3 |
Tentukan mean berat badan mahasiswa di universitas tersebut.
Kunci Jawaban dan Pembahasan Soal 5
Kita akan menggunakan metode yang sama seperti pada soal sebelumnya untuk menghitung mean berat badan mahasiswa di universitas tersebut.
| Berat Badan (kg) | Frekuensi (f) | Titik Tengah (x) | f * x |
|---|---|---|---|
| 45 – 50 | 10 | 47,5 | 475 |
| 50 – 55 | 15 | 52,5 | 787,5 |
| 55 – 60 | 20 | 57,5 | 1150 |
| 60 – 65 | 12 | 62,5 | 750 |
| 65 – 70 | 3 | 67,5 | 202,5 |
| Total | 60 | 3365 |
Mean berat badan mahasiswa di universitas tersebut adalah:
Mean = Σ(f * x) / Σf = 3365 / 60 = 56,08 kg
Jadi, mean berat badan mahasiswa di universitas tersebut adalah 56,08 kg.
Sumber Belajar Tambahan
- Buku pelajaran matematika SMA/MA kelas X
- Website resmi Kemdikbud
- Website Khan Academy
- Video tutorial di YouTube
Terakhir
Memahami konsep mean data berkelompok tidak hanya penting dalam dunia akademis, tetapi juga bermanfaat dalam kehidupan sehari-hari. Dengan memahami cara menghitung mean data berkelompok, Anda dapat menganalisis data yang terkelompokkan, menarik kesimpulan yang akurat, dan mengambil keputusan yang tepat berdasarkan informasi yang Anda peroleh.






