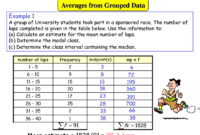
Contoh soal mean median modus dan jawabannya kelas 6 sd – Belajar tentang mean, median, dan modus memang menyenangkan, terutama saat kita bisa langsung mempraktikkannya dengan contoh soal. Nah, bagi kamu yang duduk di kelas 6 SD, pasti sudah mulai belajar tentang cara menghitung rata-rata, nilai tengah, dan data yang paling sering muncul dalam suatu kumpulan data. Yuk, kita kulik lebih dalam tentang mean, median, dan modus dengan beberapa contoh soal dan jawabannya yang mudah dipahami!
Contoh soal mean, median, dan modus sering muncul dalam buku pelajaran matematika kelas 6 SD. Materi ini membantu kita memahami cara menganalisis data dan menemukan informasi penting dari kumpulan data. Contoh soal yang akan kita bahas akan membantu kamu lebih memahami konsep dan cara menghitung mean, median, dan modus dengan mudah.
Pengertian Mean, Median, dan Modus
Dalam matematika, khususnya statistika, mean, median, dan modus adalah tiga ukuran tendensi sentral yang sering digunakan untuk menggambarkan kumpulan data numerik. Ketiga ukuran ini membantu kita memahami karakteristik utama dari data, seperti nilai tengah, nilai yang paling sering muncul, dan nilai rata-rata.
Mean
Mean, yang juga dikenal sebagai rata-rata, adalah nilai tengah dari kumpulan data. Mean dihitung dengan menjumlahkan semua nilai dalam data dan kemudian membaginya dengan jumlah nilai dalam data tersebut.
Mean = (Jumlah semua nilai dalam data) / (Jumlah nilai dalam data)
Contohnya, jika kita memiliki kumpulan data: 2, 4, 6, 8, 10. Maka mean dari data tersebut adalah:
Mean = (2 + 4 + 6 + 8 + 10) / 5 = 30 / 5 = 6
Median
Median adalah nilai tengah dari kumpulan data yang telah diurutkan dari yang terkecil hingga yang terbesar. Jika jumlah data ganjil, maka median adalah nilai tengah. Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengah.
Nah, kalau kamu udah ngerti tentang contoh soal mean median modus dan jawabannya kelas 6 SD, mungkin kamu juga tertarik untuk belajar tentang konsep fisika seperti gerak jatuh bebas dan gerak vertikal ke atas. Untuk ngebantu kamu memahami materi ini, kamu bisa cek contoh soal dan pembahasannya di contoh soal gerak jatuh bebas dan gerak vertikal ke atas.
Setelah itu, kamu bisa kembali ke contoh soal mean median modus dan jawabannya kelas 6 SD untuk memperdalam pemahamanmu tentang statistik dasar.
Contohnya, jika kita memiliki kumpulan data: 2, 4, 6, 8, 10. Maka median dari data tersebut adalah 6, karena 6 adalah nilai tengah setelah data diurutkan.
Contoh lainnya, jika kita memiliki kumpulan data: 2, 4, 6, 8. Maka median dari data tersebut adalah (4 + 6) / 2 = 5, karena 4 dan 6 adalah dua nilai tengah setelah data diurutkan.
Modus
Modus adalah nilai yang paling sering muncul dalam kumpulan data. Kumpulan data dapat memiliki satu modus (unimodal), dua modus (bimodal), atau lebih dari dua modus (multimodal). Jika semua nilai dalam data muncul hanya sekali, maka data tersebut tidak memiliki modus.
Contohnya, jika kita memiliki kumpulan data: 2, 4, 6, 6, 8, 10. Maka modus dari data tersebut adalah 6, karena 6 muncul dua kali, lebih sering dibandingkan nilai lainnya.
Cara Menghitung Median: Contoh Soal Mean Median Modus Dan Jawabannya Kelas 6 Sd
Median merupakan nilai tengah dari suatu kumpulan data yang telah diurutkan dari yang terkecil hingga yang terbesar. Median berguna untuk mengetahui nilai tengah dari data yang ada.
Langkah-Langkah Menghitung Median
Untuk menghitung median, ada beberapa langkah yang perlu dilakukan, yaitu:
- Urutkan data dari yang terkecil hingga yang terbesar.
- Jika jumlah data ganjil, median adalah nilai tengah dari data yang telah diurutkan.
- Jika jumlah data genap, median adalah rata-rata dari dua nilai tengah dari data yang telah diurutkan.
Contoh Soal Menghitung Median
Misalkan kita memiliki data nilai ulangan matematika 6 siswa sebagai berikut:
70, 80, 60, 90, 75, 85
Langkah-langkah menghitung mediannya adalah:
- Urutkan data dari yang terkecil hingga yang terbesar: 60, 70, 75, 80, 85, 90.
- Jumlah data adalah 6 (genap), sehingga median adalah rata-rata dari dua nilai tengah, yaitu 75 dan 80.
- Median = (75 + 80) / 2 = 77,5
Jadi, median dari data nilai ulangan matematika 6 siswa tersebut adalah 77,5.
Ilustrasi Menghitung Median
Berikut ilustrasi proses penghitungan median dari data yang terdiri dari 6 nilai:
Data nilai ulangan matematika 6 siswa: 70, 80, 60, 90, 75, 85.
- Urutkan data dari yang terkecil hingga yang terbesar: 60, 70, 75, 80, 85, 90.
- Karena jumlah data genap, maka median adalah rata-rata dari dua nilai tengah: 75 dan 80.
- Median = (75 + 80) / 2 = 77,5
Ilustrasi ini menunjukkan bahwa median adalah nilai tengah dari data yang telah diurutkan. Jika jumlah data genap, maka median adalah rata-rata dari dua nilai tengah.
Aplikasi Mean, Median, dan Modus dalam Kehidupan Sehari-hari
Mean, median, dan modus merupakan konsep dalam statistika yang sering kita jumpai dalam kehidupan sehari-hari. Ketiga konsep ini membantu kita dalam memahami dan menganalisis data, sehingga dapat membantu dalam pengambilan keputusan.
Contoh Penerapan Mean, Median, dan Modus, Contoh soal mean median modus dan jawabannya kelas 6 sd
Berikut beberapa contoh situasi nyata di mana mean, median, dan modus dapat diterapkan:
- Menghitung Rata-rata Nilai Ujian: Misalkan kamu ingin mengetahui nilai rata-rata ujian matematika kelasmu. Kamu dapat menggunakan mean untuk menghitungnya. Mean diperoleh dengan menjumlahkan semua nilai ujian dan membaginya dengan jumlah siswa.
- Menentukan Gaji Tengah: Perusahaan ingin mengetahui gaji tengah karyawannya. Median dapat digunakan untuk menentukannya. Median adalah nilai tengah dari data yang telah diurutkan dari yang terkecil hingga yang terbesar.
- Menganalisis Tren Penjualan: Toko pakaian ingin mengetahui ukuran baju yang paling banyak terjual. Modus dapat digunakan untuk menentukan ukuran baju yang paling populer. Modus adalah nilai yang paling sering muncul dalam data.
Manfaat Penerapan Mean, Median, dan Modus
Penerapan mean, median, dan modus dalam situasi di atas dapat membantu dalam pengambilan keputusan. Berikut contoh manfaatnya:
- Menghitung Rata-rata Nilai Ujian: Mean dapat membantu guru untuk mengetahui performa rata-rata siswa dalam mata pelajaran tertentu. Informasi ini dapat digunakan untuk menilai efektivitas metode pembelajaran dan untuk mengidentifikasi siswa yang membutuhkan bantuan tambahan.
- Menentukan Gaji Tengah: Median dapat membantu perusahaan dalam menentukan gaji yang adil bagi karyawannya. Informasi ini juga dapat digunakan untuk membandingkan gaji karyawan dengan perusahaan lain di industri yang sama.
- Menganalisis Tren Penjualan: Modus dapat membantu toko pakaian dalam menentukan ukuran baju yang paling banyak diminati oleh pelanggan. Informasi ini dapat digunakan untuk mengoptimalkan persediaan dan meminimalkan pemborosan.
Tabel Contoh Penerapan Mean, Median, dan Modus
Berikut tabel yang berisi contoh situasi nyata, jenis data yang digunakan, dan manfaat penerapan mean, median, dan modus:
| Situasi | Jenis Data | Manfaat |
|---|---|---|
| Menghitung Rata-rata Nilai Ujian | Nilai Ujian | Menilai performa rata-rata siswa, mengidentifikasi siswa yang membutuhkan bantuan tambahan |
| Menentukan Gaji Tengah | Gaji Karyawan | Menentukan gaji yang adil, membandingkan gaji dengan perusahaan lain |
| Menganalisis Tren Penjualan | Ukuran Baju yang Terjual | Menganalisis tren penjualan, mengoptimalkan persediaan |
Pentingnya Memahami Mean, Median, dan Modus
Dalam pembelajaran matematika, memahami konsep mean, median, dan modus bukan hanya sekadar belajar rumus. Ketiga konsep ini merupakan alat yang sangat berguna untuk menganalisis data dan memahami pola dalam kehidupan sehari-hari.
Manfaat Memahami Mean, Median, dan Modus
Memahami konsep mean, median, dan modus memiliki banyak manfaat, baik dalam pembelajaran matematika maupun dalam kehidupan sehari-hari. Ketiga konsep ini membantu kita untuk:
- Menganalisis data: Mean, median, dan modus membantu kita untuk mendapatkan gambaran umum tentang suatu set data. Mean menunjukkan nilai rata-rata, median menunjukkan nilai tengah, dan modus menunjukkan nilai yang paling sering muncul.
- Membuat keputusan yang lebih baik: Dengan memahami mean, median, dan modus, kita dapat membuat keputusan yang lebih tepat berdasarkan data yang tersedia. Misalnya, jika kita ingin mengetahui rata-rata nilai ujian siswa, kita dapat menghitung mean.
- Membandingkan data: Ketiga konsep ini juga dapat membantu kita untuk membandingkan data dari sumber yang berbeda. Misalnya, kita dapat membandingkan rata-rata nilai ujian di dua kelas yang berbeda.
Contoh Penerapan Mean, Median, dan Modus dalam Kehidupan Sehari-hari
Berikut adalah beberapa contoh bagaimana konsep mean, median, dan modus dapat diterapkan dalam kehidupan sehari-hari:
- Menghitung nilai rata-rata: Misalkan kamu ingin mengetahui nilai rata-rata ulangan matematika di kelasmu. Kamu dapat menghitung mean dari semua nilai ulangan tersebut.
- Menentukan nilai tengah: Misalkan kamu ingin mengetahui nilai tengah dari harga 5 jenis baju yang berbeda. Kamu dapat menghitung median dari harga kelima baju tersebut.
- Menentukan ukuran sepatu yang paling populer: Misalkan kamu adalah seorang pemilik toko sepatu. Kamu dapat menggunakan modus untuk mengetahui ukuran sepatu yang paling banyak dibeli oleh pelanggan.
Latihan Soal Mean, Median, dan Modus
Menghitung mean, median, dan modus adalah keterampilan penting dalam matematika. Ketiga ukuran ini membantu kita memahami data dengan lebih baik. Mean menunjukkan nilai rata-rata, median menunjukkan nilai tengah, dan modus menunjukkan nilai yang paling sering muncul. Mari kita coba mengerjakan beberapa latihan soal untuk memperdalam pemahaman kita tentang mean, median, dan modus!
Latihan Soal Mean, Median, dan Modus
Berikut adalah 5 soal latihan yang melibatkan perhitungan mean, median, dan modus. Soal-soal ini dirancang untuk membantu kamu memahami konsep-konsep tersebut dengan lebih baik.
| No. | Soal | Kunci Jawaban |
|---|---|---|
| 1. | Ibu membeli 5 buah apel dengan berat 100 gram, 120 gram, 110 gram, 130 gram, dan 140 gram. Berapakah berat rata-rata (mean) dari 5 buah apel tersebut? | 120 gram |
| 2. | Nilai ulangan matematika 7 siswa adalah 80, 75, 90, 85, 80, 95, dan 80. Tentukan nilai median dari data tersebut! | 80 |
| 3. | Di dalam sebuah kelas terdapat 20 siswa. 10 siswa menyukai pelajaran matematika, 5 siswa menyukai pelajaran bahasa Indonesia, dan 5 siswa menyukai pelajaran IPA. Tentukan modus dari data tersebut! | Matematika |
| 4. | Rata-rata tinggi badan 5 orang siswa adalah 155 cm. Jika tinggi badan 4 siswa tersebut adalah 150 cm, 160 cm, 158 cm, dan 152 cm, tentukan tinggi badan siswa ke-5! | 160 cm |
| 5. | Data nilai ujian Bahasa Inggris dari 10 siswa adalah: 70, 80, 85, 75, 80, 90, 70, 85, 80, 95. Tentukan mean, median, dan modus dari data tersebut! | Mean: 81, Median: 80, Modus: 80 |
Kesimpulan
Memahami mean, median, dan modus bukan hanya untuk menyelesaikan soal matematika, tapi juga berguna dalam kehidupan sehari-hari. Dengan menguasai konsep ini, kita dapat menganalisis data, membuat keputusan yang lebih baik, dan bahkan memahami pola-pola yang terjadi di sekitar kita. Jadi, teruslah belajar dan berlatih agar kamu semakin mahir dalam menguasai mean, median, dan modus!