Contoh soal nilai mutlak dan pembahasannya pdf – Mempelajari konsep nilai mutlak bisa terasa membingungkan, terutama saat dihadapkan dengan soal-soal yang kompleks. Namun, jangan khawatir! Artikel ini akan memandu Anda memahami konsep nilai mutlak dengan mudah melalui contoh soal dan pembahasannya yang disusun dalam format PDF.
Dari definisi nilai mutlak hingga aplikasi praktisnya dalam kehidupan sehari-hari, artikel ini akan menguraikan semua aspek penting yang perlu Anda ketahui. Dengan panduan langkah demi langkah, Anda akan mampu menyelesaikan soal-soal nilai mutlak dengan percaya diri dan meraih hasil belajar yang optimal.
Pengertian Nilai Mutlak
Nilai mutlak, dalam matematika, merupakan konsep yang mengukur jarak suatu bilangan dari nol pada garis bilangan. Konsep ini sering dijumpai dalam berbagai bidang, seperti geometri, fisika, dan ilmu komputer. Dalam kehidupan sehari-hari, nilai mutlak bisa dianalogikan dengan jarak tempuh, tanpa mempertimbangkan arah. Misalnya, jika Anda berjalan 5 meter ke utara, kemudian 5 meter ke selatan, total jarak tempuh Anda adalah 10 meter, meskipun posisi akhir Anda sama dengan posisi awal.
Contoh Nilai Mutlak
Berikut adalah tabel yang menunjukkan nilai mutlak dari beberapa bilangan bulat, pecahan, dan desimal:
| Bilangan | Nilai Mutlak |
|---|---|
| -5 | 5 |
| 3 | 3 |
| -1/2 | 1/2 |
| 2.5 | 2.5 |
Sifat-Sifat Nilai Mutlak
Nilai mutlak merupakan konsep penting dalam matematika yang merepresentasikan jarak suatu bilangan dari nol pada garis bilangan. Sifat-sifat nilai mutlak membantu kita dalam memahami dan menyelesaikan berbagai persamaan, pertidaksamaan, dan masalah yang melibatkan nilai mutlak.
Sifat-Sifat Utama Nilai Mutlak
Lima sifat utama nilai mutlak yang perlu dipahami adalah:
- Sifat 1: Non-Negatif
- Sifat 2: Simetri
- Sifat 3: Produk
- Sifat 4: Kuadrat
- Sifat 5: Ketidaksamaan Segitiga
Nilai mutlak dari setiap bilangan real selalu non-negatif. Artinya, nilai mutlak suatu bilangan tidak pernah bernilai negatif.
|x| ≥ 0 untuk setiap x ∈ R
Contoh: |5| = 5 dan |-5| = 5. Keduanya bernilai positif.
Nilai mutlak dari suatu bilangan sama dengan nilai mutlak dari negatifnya.
|x| = |-x| untuk setiap x ∈ R
Contoh: |3| = |-3| = 3.
Nilai mutlak dari hasil kali dua bilangan sama dengan hasil kali nilai mutlak dari masing-masing bilangan tersebut.
|x * y| = |x| * |y| untuk setiap x, y ∈ R
Contoh: |2 * (-3)| = |2| * |-3| = 6.
Kuadrat dari nilai mutlak suatu bilangan sama dengan kuadrat dari bilangan tersebut.
|x|² = x² untuk setiap x ∈ R
Contoh: |4|² = 4² = 16.
Nilai mutlak dari jumlah dua bilangan selalu lebih kecil atau sama dengan jumlah nilai mutlak dari masing-masing bilangan tersebut.
|x + y| ≤ |x| + |y| untuk setiap x, y ∈ R
Contoh: |2 + 3| ≤ |2| + |3|, karena 5 ≤ 5.
Contoh Aplikasi Sifat-Sifat Nilai Mutlak
Berikut contoh aplikasi dari masing-masing sifat nilai mutlak dalam bentuk persamaan atau pertidaksamaan:
| Sifat | Contoh | Penjelasan |
|---|---|---|
| Non-Negatif | |x| ≥ 0 | Nilai mutlak dari x selalu lebih besar atau sama dengan nol. |
| Simetri | |x| = |-x| | Nilai mutlak dari x sama dengan nilai mutlak dari negatif x. |
| Produk | |x * y| = |x| * |y| | Nilai mutlak dari hasil kali x dan y sama dengan hasil kali nilai mutlak x dan y. |
| Kuadrat | |x|² = x² | Kuadrat dari nilai mutlak x sama dengan kuadrat dari x. |
| Ketidaksamaan Segitiga | |x + y| ≤ |x| + |y| | Nilai mutlak dari jumlah x dan y selalu lebih kecil atau sama dengan jumlah nilai mutlak x dan y. |
Menyelesaikan Persamaan Nilai Mutlak
Persamaan nilai mutlak adalah persamaan yang memuat fungsi nilai mutlak. Fungsi nilai mutlak dari suatu bilangan adalah jarak bilangan tersebut dari nol. Nilai mutlak selalu bernilai positif atau nol.
Untuk menyelesaikan persamaan nilai mutlak, kita perlu memahami sifat-sifat dari fungsi nilai mutlak. Sifat yang paling penting adalah bahwa nilai mutlak suatu bilangan akan bernilai nol jika bilangan tersebut bernilai nol. Dengan memahami sifat ini, kita dapat menyelesaikan persamaan nilai mutlak dengan mudah.
Langkah-langkah Menyelesaikan Persamaan Nilai Mutlak
Langkah-langkah umum dalam menyelesaikan persamaan nilai mutlak adalah sebagai berikut:
- Tentukan nilai mutlak dari variabel dalam persamaan.
- Tentukan nilai variabel yang membuat nilai mutlak tersebut bernilai nol.
- Selesaikan persamaan untuk variabel tersebut.
Contoh Soal Persamaan Nilai Mutlak Sederhana
Misalnya, kita ingin menyelesaikan persamaan nilai mutlak berikut:
|x – 2| = 5
Langkah-langkah penyelesaiannya adalah sebagai berikut:
- Tentukan nilai mutlak dari variabel dalam persamaan. Dalam kasus ini, nilai mutlak dari variabel x – 2 adalah 5.
- Tentukan nilai variabel yang membuat nilai mutlak tersebut bernilai nol. Dalam kasus ini, nilai x yang membuat nilai mutlak |x – 2| bernilai nol adalah x = 2.
- Selesaikan persamaan untuk variabel tersebut. Karena nilai mutlak |x – 2| bernilai 5, maka nilai x – 2 dapat bernilai 5 atau -5. Dengan demikian, kita mendapatkan dua persamaan:
- x – 2 = 5
- x – 2 = -5
Selesaikan kedua persamaan tersebut untuk mendapatkan nilai x. Dari persamaan pertama, kita dapatkan x = 7. Dari persamaan kedua, kita dapatkan x = -3.
Jadi, solusi dari persamaan nilai mutlak |x – 2| = 5 adalah x = 7 atau x = -3.
Contoh Soal Persamaan Nilai Mutlak dengan Berbagai Jenis Kasus
Berikut adalah beberapa contoh soal persamaan nilai mutlak dengan berbagai jenis kasus dan penyelesaiannya:
| No | Persamaan | Penyelesaian |
|---|---|---|
| 1 | |x| = 3 | x = 3 atau x = -3 |
| 2 | |2x – 1| = 5 | x = 3 atau x = -2 |
| 3 | |x + 4| = 0 | x = -4 |
| 4 | |x – 1| = |x + 3| | x = -1 |
Menyelesaikan Pertidaksamaan Nilai Mutlak
Pertidaksamaan nilai mutlak merupakan bentuk pertidaksamaan yang melibatkan operasi nilai mutlak. Untuk menyelesaikannya, diperlukan pemahaman tentang sifat nilai mutlak dan penerapannya dalam pertidaksamaan.
Langkah-langkah Umum Menyelesaikan Pertidaksamaan Nilai Mutlak
Berikut langkah-langkah umum dalam menyelesaikan pertidaksamaan nilai mutlak:
- Tentukan bentuk pertidaksamaan. Pastikan pertidaksamaan sudah dalam bentuk yang melibatkan operasi nilai mutlak.
- Identifikasi kasus-kasus yang mungkin terjadi. Pertidaksamaan nilai mutlak memiliki beberapa kasus yang perlu dipertimbangkan, tergantung pada nilai di dalam tanda nilai mutlak.
- Selesaikan pertidaksamaan untuk setiap kasus. Setiap kasus akan menghasilkan pertidaksamaan linear yang lebih mudah diselesaikan.
- Gabungkan solusi dari setiap kasus. Solusi akhir diperoleh dengan menggabungkan solusi dari semua kasus yang mungkin terjadi.
Contoh Soal Pertidaksamaan Nilai Mutlak Sederhana
Misalnya, kita ingin menyelesaikan pertidaksamaan nilai mutlak berikut:
|x – 2| < 3
Berikut langkah-langkah penyelesaiannya:
- Tentukan bentuk pertidaksamaan. Pertidaksamaan sudah dalam bentuk yang melibatkan operasi nilai mutlak.
- Identifikasi kasus-kasus yang mungkin terjadi. Ada dua kasus yang mungkin terjadi:
- Kasus 1: x – 2 ≥ 0. Dalam kasus ini, |x – 2| = x – 2.
- Kasus 2: x – 2 < 0. Dalam kasus ini, |x – 2| = -(x – 2) = 2 – x.
- Selesaikan pertidaksamaan untuk setiap kasus:
- Kasus 1: x – 2 ≥ 0.
- x – 2 < 3
- x < 5
- Kasus 2: x – 2 < 0.
- 2 – x < 3
- -x < 1
- x > -1
- Kasus 1: x – 2 ≥ 0.
- Gabungkan solusi dari setiap kasus. Solusi akhir diperoleh dengan menggabungkan solusi dari kedua kasus: -1 < x < 5.
Contoh Soal Pertidaksamaan Nilai Mutlak dengan Berbagai Jenis Kasus
Berikut adalah tabel yang berisi contoh soal pertidaksamaan nilai mutlak dengan berbagai jenis kasus dan penyelesaiannya:
| No | Soal | Kasus | Penyelesaian | Solusi |
|---|---|---|---|---|
| 1 | |x + 1| > 2 | x + 1 > 0 atau x + 1 < 0 | x > 1 atau x < -3 | x 1 |
| 2 | |2x – 3| ≤ 5 | 2x – 3 ≥ 0 atau 2x – 3 < 0 | x ≥ 3/2 atau x < 3/2 | -1 ≤ x ≤ 4 |
| 3 | |x – 4| + 2 < 7 | x – 4 ≥ 0 atau x – 4 < 0 | x ≥ 4 atau x < 4 | 1 < x < 9 |
Aplikasi Nilai Mutlak dalam Kehidupan Sehari-hari
Nilai mutlak, yang dilambangkan dengan tanda garis vertikal (| |), merupakan konsep matematika yang sering muncul dalam berbagai bidang kehidupan. Nilai mutlak dari suatu bilangan adalah jarak bilangan tersebut dari nol, tanpa mempertimbangkan arah. Konsep ini membantu dalam mengukur jarak, selisih, dan kesalahan, yang sangat berguna dalam berbagai bidang, seperti fisika, ekonomi, dan ilmu komputer.
Pengukuran Jarak dan Selisih
Dalam fisika, nilai mutlak digunakan untuk menghitung jarak antara dua titik. Misalnya, jika kita ingin menghitung jarak antara dua kota A dan B, kita dapat menggunakan rumus jarak:
Jarak = |Posisi A – Posisi B|
Nilai mutlak memastikan bahwa jarak yang dihasilkan selalu positif, terlepas dari urutan posisi kota A dan B.
Contoh lain, dalam ilmu komputer, nilai mutlak digunakan untuk menghitung jarak antara dua titik pada bidang koordinat. Hal ini berguna dalam aplikasi seperti navigasi GPS dan pengolahan citra.
Pengukuran Kesalahan, Contoh soal nilai mutlak dan pembahasannya pdf
Dalam ilmu pengetahuan, nilai mutlak digunakan untuk menghitung kesalahan atau deviasi dari nilai sebenarnya. Misalnya, dalam eksperimen fisika, nilai mutlak dapat digunakan untuk menghitung selisih antara nilai hasil eksperimen dan nilai teoritis.
Kesalahan = |Nilai Hasil – Nilai Teoritis|
Nilai mutlak menjamin bahwa kesalahan selalu diukur sebagai nilai positif, terlepas dari apakah nilai hasil lebih besar atau lebih kecil dari nilai teoritis.
Contoh Aplikasi dalam Kehidupan Sehari-hari
Berikut beberapa contoh aplikasi nilai mutlak dalam kehidupan sehari-hari:
- Perbedaan Suhu: Ketika kita ingin mengetahui perbedaan suhu antara pagi dan sore, kita menggunakan nilai mutlak untuk menghitung selisihnya. Misalnya, jika suhu pagi adalah 15 derajat Celcius dan suhu sore adalah 28 derajat Celcius, maka selisih suhunya adalah |15 – 28| = 13 derajat Celcius.
- Perbedaan Harga: Ketika kita ingin mengetahui perbedaan harga antara dua produk, kita menggunakan nilai mutlak untuk menghitung selisihnya. Misalnya, jika harga produk A adalah Rp 100.000 dan harga produk B adalah Rp 120.000, maka selisih harganya adalah |100.000 – 120.000| = Rp 20.000.
- Kecepatan: Dalam fisika, kecepatan didefinisikan sebagai laju perubahan posisi terhadap waktu. Kecepatan dapat berupa nilai positif atau negatif, tergantung pada arah gerakan. Namun, ketika kita ingin mengetahui seberapa cepat suatu objek bergerak, kita menggunakan nilai mutlak dari kecepatan, yang disebut dengan “kecepatan”.
Soal Latihan Nilai Mutlak
Nilai mutlak merupakan konsep penting dalam matematika yang memiliki berbagai aplikasi dalam berbagai bidang, seperti fisika, ekonomi, dan ilmu komputer. Untuk memahami konsep ini dengan baik, latihan soal merupakan cara yang efektif. Berikut adalah 5 soal latihan tentang nilai mutlak yang meliputi persamaan, pertidaksamaan, dan aplikasi nilai mutlak. Soal-soal ini dirancang untuk membantu Anda mengasah kemampuan dalam menyelesaikan masalah yang melibatkan nilai mutlak.
Soal Latihan Nilai Mutlak
Soal-soal latihan nilai mutlak ini akan membantu Anda memahami konsep nilai mutlak dan mengaplikasikannya dalam berbagai situasi. Soal-soal ini disusun dengan format tabel yang mudah dibaca dan dipahami.
| No | Soal | Kunci Jawaban |
|---|---|---|
| 1 | Tentukan himpunan penyelesaian dari persamaan |2x – 3| = 5. | x = 4 atau x = -1 |
| 2 | Tentukan himpunan penyelesaian dari pertidaksamaan |x + 1| < 3. | -4 < x < 2 |
| 3 | Sebuah mobil melaju dengan kecepatan 60 km/jam. Jarak yang ditempuh mobil tersebut dalam waktu t jam dapat dinyatakan dengan persamaan s = 60t. Jika kecepatan mobil tersebut dapat bervariasi sebesar 10 km/jam, tentukan batas waktu yang diperlukan mobil untuk menempuh jarak 150 km. | 1,5 jam < t < 2,5 jam |
| 4 | Tentukan nilai minimum dari fungsi f(x) = |x – 2| + |x + 3|. | 5 |
| 5 | Tentukan himpunan penyelesaian dari pertidaksamaan |2x – 1| > 3. | x < -1 atau x > 2 |
Pembahasan Soal Nilai Mutlak
Pada bagian ini, kita akan membahas dua contoh soal nilai mutlak yang telah kita temui sebelumnya. Dengan mempelajari langkah-langkah penyelesaiannya, kita dapat memahami lebih dalam konsep nilai mutlak dan bagaimana menerapkannya dalam menyelesaikan masalah.
Contoh Soal 1
Berikut adalah contoh soal nilai mutlak pertama yang akan kita bahas:
Tentukan himpunan penyelesaian dari persamaan |2x – 3| = 5.
Untuk menyelesaikan persamaan nilai mutlak ini, kita dapat menggunakan definisi nilai mutlak. Definisi nilai mutlak menyatakan bahwa nilai mutlak suatu bilangan adalah jarak bilangan tersebut dari nol. Dengan demikian, kita dapat menulis persamaan tersebut dalam dua bentuk:
- 2x – 3 = 5
- 2x – 3 = -5
Selanjutnya, kita dapat menyelesaikan kedua persamaan tersebut untuk mendapatkan nilai x:
- 2x – 3 = 5 => 2x = 8 => x = 4
- 2x – 3 = -5 => 2x = -2 => x = -1
Jadi, himpunan penyelesaian dari persamaan |2x – 3| = 5 adalah 4, -1.
Contoh Soal 2
Contoh soal nilai mutlak kedua yang akan kita bahas adalah:
Tentukan nilai x yang memenuhi pertidaksamaan |x + 1| < 3.
Pertidaksamaan nilai mutlak ini dapat dipecahkan dengan menggunakan konsep jarak. Karena nilai mutlak menyatakan jarak dari nol, maka pertidaksamaan tersebut dapat diartikan sebagai “jarak x + 1 dari nol kurang dari 3”.
Dengan demikian, kita dapat menulis pertidaksamaan tersebut dalam bentuk:
- -3 < x + 1 < 3
Selanjutnya, kita dapat menyelesaikan pertidaksamaan tersebut:
- -3 < x + 1 -4 < x < 2
Jadi, nilai x yang memenuhi pertidaksamaan |x + 1| < 3 adalah -4 < x < 2.
Kumpulan Soal Nilai Mutlak dan Pembahasannya
Nilai mutlak merupakan konsep penting dalam matematika yang memiliki banyak aplikasi dalam berbagai bidang, seperti fisika, ekonomi, dan ilmu komputer. Memahami konsep nilai mutlak dan cara menyelesaikan soal-soal yang berkaitan dengannya sangat penting untuk meningkatkan kemampuan matematika Anda.
Artikel ini menyajikan kumpulan soal nilai mutlak beserta pembahasannya. Soal-soal ini dirancang untuk membantu Anda memahami konsep nilai mutlak dengan lebih baik dan meningkatkan kemampuan Anda dalam menyelesaikan soal-soal yang berkaitan dengan nilai mutlak.
Pengertian Nilai Mutlak
Nilai mutlak dari suatu bilangan adalah jarak bilangan tersebut dari nol pada garis bilangan. Nilai mutlak dari bilangan x dilambangkan dengan |x|.
Latihan soal nilai mutlak dan pembahasannya PDF memang penting untuk memahami konsepnya. Selain itu, kamu juga bisa melatih kemampuanmu dengan mengerjakan soal-soal lain, seperti contoh soal unsur periode 3. Materi kimia seperti ini juga bisa dikaitkan dengan konsep nilai mutlak, lho.
Misalnya, dalam menghitung konsentrasi larutan, kita bisa menggunakan rumus yang melibatkan nilai mutlak. Jadi, belajarlah dengan tekun agar kamu bisa menguasai semua materi dengan baik!
Sebagai contoh, nilai mutlak dari 3 adalah 3, karena jarak 3 dari nol pada garis bilangan adalah 3. Nilai mutlak dari -3 juga 3, karena jarak -3 dari nol pada garis bilangan juga 3.
|x| = x, jika x ≥ 0
|x| = -x, jika x < 0
Sifat-Sifat Nilai Mutlak
Nilai mutlak memiliki beberapa sifat yang dapat digunakan untuk menyelesaikan soal-soal yang berkaitan dengan nilai mutlak. Berikut adalah beberapa sifat nilai mutlak:
- |x| ≥ 0 untuk setiap bilangan real x.
- |x| = |-x| untuk setiap bilangan real x.
- |x|² = x² untuk setiap bilangan real x.
- |x + y| ≤ |x| + |y| untuk setiap bilangan real x dan y.
Soal dan Pembahasan
Berikut adalah beberapa contoh soal nilai mutlak beserta pembahasannya:
Contoh Soal 1
Tentukan nilai mutlak dari -5.
Pembahasan:
Nilai mutlak dari -5 adalah 5, karena jarak -5 dari nol pada garis bilangan adalah 5. Jadi, |-5| = 5.
Contoh Soal 2
Selesaikan persamaan |x – 2| = 3.
Pembahasan:
Persamaan |x – 2| = 3 memiliki dua solusi, yaitu:
- x – 2 = 3, sehingga x = 5
- x – 2 = -3, sehingga x = -1
Jadi, solusi dari persamaan |x – 2| = 3 adalah x = 5 atau x = -1.
Contoh Soal 3
Tentukan nilai x yang memenuhi pertidaksamaan |x + 1| < 2.
Pembahasan:
Pertidaksamaan |x + 1| < 2 memiliki dua solusi, yaitu:
- x + 1 < 2, sehingga x < 1
- x + 1 > -2, sehingga x > -3
Jadi, nilai x yang memenuhi pertidaksamaan |x + 1| < 2 adalah -3 < x < 1.
Kesimpulan
Soal-soal nilai mutlak dapat diselesaikan dengan memahami konsep nilai mutlak dan sifat-sifatnya. Dengan latihan yang cukup, Anda akan dapat menyelesaikan soal-soal nilai mutlak dengan mudah dan percaya diri.
Tips Mempelajari Nilai Mutlak
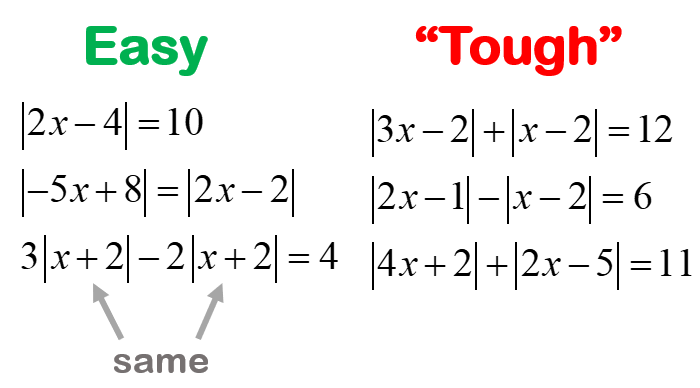
Nilai mutlak merupakan konsep penting dalam matematika yang sering dijumpai dalam berbagai bidang, seperti geometri, aljabar, dan kalkulus. Memahami konsep ini dengan baik akan memudahkan kamu dalam menyelesaikan berbagai macam soal matematika. Berikut adalah beberapa tips efektif untuk mempelajari nilai mutlak dan meningkatkan kemampuan dalam menyelesaikan soal-soal terkait.
Memahami Definisi Nilai Mutlak
Langkah pertama dalam mempelajari nilai mutlak adalah memahami definisinya. Nilai mutlak dari suatu bilangan adalah jarak bilangan tersebut dari nol pada garis bilangan. Hal ini dapat diartikan sebagai besarnya nilai bilangan tanpa memperhatikan tanda positif atau negatifnya.
- Jika bilangan tersebut positif, maka nilai mutlaknya sama dengan bilangan itu sendiri. Contoh: |5| = 5.
- Jika bilangan tersebut negatif, maka nilai mutlaknya sama dengan lawan dari bilangan itu. Contoh: |-3| = 3.
- Nilai mutlak dari nol adalah nol. Contoh: |0| = 0.
Menerapkan Rumus dan Sifat Nilai Mutlak
Setelah memahami definisi, kamu perlu mempelajari rumus dan sifat-sifat nilai mutlak. Rumus ini akan membantu kamu dalam menyelesaikan soal-soal yang lebih kompleks. Beberapa rumus dan sifat penting yang perlu kamu ketahui:
- |x| = x jika x ≥ 0 dan |x| = -x jika x < 0.
- |x| ≥ 0 untuk semua nilai x.
- |x| = |-x| untuk semua nilai x.
- |x + y| ≤ |x| + |y| (Ketidaksamaan segitiga).
Melatih Soal-Soal
Untuk menguasai konsep nilai mutlak, latihan soal merupakan kunci. Mulailah dengan soal-soal dasar dan secara bertahap tingkatkan tingkat kesulitannya. Saat mengerjakan soal, perhatikan langkah-langkah penyelesaian dan pahami konsep di balik setiap langkah. Kamu juga dapat memanfaatkan buku latihan, website, atau video tutorial untuk mendapatkan soal-soal tambahan.
Sumber Belajar Tambahan
Selain buku teks, kamu dapat menemukan sumber belajar tambahan untuk mempelajari nilai mutlak, seperti:
- Buku: “Matematika SMA Kelas X” oleh Erlangga, “Buku Pintar Matematika” oleh Gramedia.
- Website: Khan Academy, Ruangguru, Zenius Education.
- Video Tutorial: Youtube channel seperti “Math Easy”, “The Organic Chemistry Tutor”.
Penjelasan Lengkap Nilai Mutlak
Nilai mutlak adalah konsep matematika yang penting dan sering muncul dalam berbagai bidang seperti aljabar, geometri, kalkulus, dan ilmu komputer. Dalam artikel ini, kita akan membahas definisi, sifat, dan aplikasi nilai mutlak secara komprehensif.
Pengertian Nilai Mutlak
Nilai mutlak dari suatu bilangan real adalah jarak bilangan tersebut dari nol pada garis bilangan. Nilai mutlak dari suatu bilangan selalu positif atau nol.
Simpulan Akhir: Contoh Soal Nilai Mutlak Dan Pembahasannya Pdf
Dengan memahami konsep nilai mutlak melalui contoh soal dan pembahasannya, Anda tidak hanya akan mampu menyelesaikan soal-soal matematika dengan lebih mudah, tetapi juga dapat menerapkannya dalam berbagai bidang kehidupan. Segera unduh PDF-nya dan tingkatkan pemahaman Anda tentang konsep nilai mutlak sekarang!





