Contoh soal pecahan lebih besar lebih kecil – Pecahan, bagian-bagian yang membentuk keseluruhan, seringkali kita jumpai dalam kehidupan sehari-hari. Bayangkan sepotong pizza yang dibagi menjadi beberapa bagian, atau kue yang dipotong menjadi beberapa irisan. Bagaimana kita bisa menentukan mana yang lebih besar, 1/2 pizza atau 1/4 pizza? Nah, di sinilah perbandingan pecahan berperan penting.
Melalui contoh soal yang menarik, kita akan menjelajahi cara membandingkan pecahan dengan penyebut sama dan berbeda, menggunakan ilustrasi gambar, teks deskriptif, frase, perbandingan langsung, dan bahkan operasi hitung. Siap-siap untuk memahami konsep perbandingan pecahan dengan cara yang mudah dan menyenangkan!
Soal Perbandingan Pecahan dengan Frase: Contoh Soal Pecahan Lebih Besar Lebih Kecil
Soal perbandingan pecahan dengan frase adalah soal yang menantang pemahamanmu tentang nilai pecahan. Dalam soal ini, kamu diminta untuk membandingkan dua pecahan yang disajikan dalam bentuk kalimat atau frasa, bukan dalam bentuk angka saja.
Misalnya, “Manakah yang lebih besar, 3/4 atau 5/6?” Soal ini menuntutmu untuk memahami nilai relatif dari kedua pecahan tersebut dan menentukan mana yang lebih besar.
Cara Menyelesaikan Soal Perbandingan Pecahan dengan Frase
Untuk menyelesaikan soal perbandingan pecahan dengan frase, ikuti langkah-langkah berikut:
- Identifikasi pecahan yang dibandingkan. Perhatikan kalimat atau frasa yang diberikan, dan cari tahu pecahan apa yang dibandingkan.
- Ubah pecahan ke bentuk yang sama. Jika pecahan yang dibandingkan memiliki penyebut yang berbeda, ubahlah keduanya ke bentuk yang sama dengan mencari kelipatan persekutuan terkecil (KPK) dari penyebutnya.
- Bandingkan pembilangnya. Setelah pecahan memiliki penyebut yang sama, bandingkan pembilangnya. Pecahan dengan pembilang yang lebih besar adalah pecahan yang lebih besar.
Contoh Soal Perbandingan Pecahan dengan Frase
| Soal | Penyelesaian |
|---|---|
| Manakah yang lebih besar, 3/4 atau 5/6? | KPK dari 4 dan 6 adalah 12. Maka, ubahlah kedua pecahan tersebut ke bentuk yang sama: 3/4 = 9/12 5/6 = 10/12 Karena 10/12 lebih besar dari 9/12, maka 5/6 lebih besar dari 3/4. |
| Manakah yang lebih kecil, 2/5 atau 3/7? | KPK dari 5 dan 7 adalah 35. Maka, ubahlah kedua pecahan tersebut ke bentuk yang sama: 2/5 = 14/35 3/7 = 15/35 Karena 14/35 lebih kecil dari 15/35, maka 2/5 lebih kecil dari 3/7. |
Soal Perbandingan Pecahan dengan Perbandingan Langsung
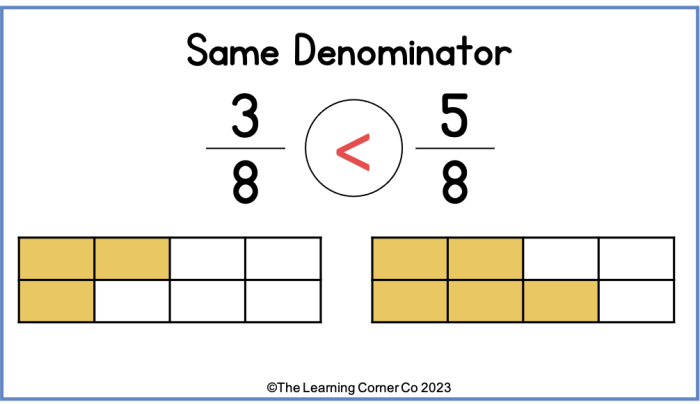
Dalam matematika, membandingkan pecahan adalah hal yang umum. Terkadang kita perlu mengetahui pecahan mana yang lebih besar, lebih kecil, atau sama dengan pecahan lainnya. Salah satu cara untuk membandingkan pecahan adalah dengan menggunakan perbandingan langsung. Perbandingan langsung dilakukan dengan membandingkan langsung nilai pecahan yang satu dengan nilai pecahan yang lainnya.
Contoh Soal Perbandingan Pecahan dengan Perbandingan Langsung
Perbandingan langsung adalah cara yang mudah untuk membandingkan pecahan dengan penyebut yang sama. Kita dapat langsung membandingkan pembilangnya untuk menentukan mana yang lebih besar atau lebih kecil.
Nah, kalau kamu lagi belajar tentang contoh soal pecahan lebih besar lebih kecil, bisa dibilang itu mirip sama memahami konsep dasar akuntansi. Misalnya, kalau kamu ingin tahu mana yang lebih besar, 1/2 atau 1/4, kamu perlu tahu bagaimana membandingkan nilai kedua pecahan tersebut.
Begitu juga dalam memahami jurnal umum perusahaan jasa, kamu perlu memahami bagaimana mencatat transaksi keuangan dengan benar. Untuk contoh soal jurnal umum perusahaan jasa, kamu bisa cek di sini: contoh soal jurnal umum perusahaan jasa. Setelah memahami konsep jurnal umum, kamu bisa kembali ke contoh soal pecahan dan melatih kemampuanmu untuk membandingkan nilai pecahan yang berbeda.
Contohnya, “Andi memiliki 1/3 bagian pizza, sedangkan Budi memiliki 2/3 bagian pizza. Berapa bagian pizza yang dimiliki Andi dibandingkan dengan Budi?”
Untuk menyelesaikan soal ini, kita bisa langsung membandingkan pembilang dari kedua pecahan. Karena 1 lebih kecil dari 2, maka Andi memiliki bagian pizza yang lebih kecil dibandingkan dengan Budi. Jadi, Andi memiliki 1/2 bagian pizza Budi.
Tabel Contoh Soal Perbandingan Pecahan dengan Perbandingan Langsung dan Penyelesaiannya
| Soal | Penyelesaian |
|---|---|
| Ani memiliki 2/5 bagian kue, sedangkan Beni memiliki 3/5 bagian kue. Berapa bagian kue yang dimiliki Ani dibandingkan dengan Beni? | Karena 2 lebih kecil dari 3, maka Ani memiliki bagian kue yang lebih kecil dibandingkan dengan Beni. Jadi, Ani memiliki 2/3 bagian kue Beni. |
| Candra memiliki 1/4 bagian apel, sedangkan Dedi memiliki 3/4 bagian apel. Berapa bagian apel yang dimiliki Candra dibandingkan dengan Dedi? | Karena 1 lebih kecil dari 3, maka Candra memiliki bagian apel yang lebih kecil dibandingkan dengan Dedi. Jadi, Candra memiliki 1/3 bagian apel Dedi. |
| Eka memiliki 2/7 bagian jeruk, sedangkan Fani memiliki 5/7 bagian jeruk. Berapa bagian jeruk yang dimiliki Eka dibandingkan dengan Fani? | Karena 2 lebih kecil dari 5, maka Eka memiliki bagian jeruk yang lebih kecil dibandingkan dengan Fani. Jadi, Eka memiliki 2/5 bagian jeruk Fani. |
Soal Perbandingan Pecahan dengan Perbandingan Tidak Langsung
Soal perbandingan pecahan dengan perbandingan tidak langsung adalah soal yang mengharuskan kita untuk membandingkan dua pecahan yang memiliki penyebut yang berbeda. Kita tidak bisa langsung membandingkan pecahan tersebut karena memiliki penyebut yang berbeda. Untuk menyelesaikannya, kita perlu mengubah kedua pecahan tersebut ke dalam bentuk pecahan yang memiliki penyebut yang sama.
Contoh Soal Perbandingan Pecahan dengan Perbandingan Tidak Langsung
Misalnya, Ibu membeli 1/2 kg apel, sedangkan Ayah membeli 1/4 kg jeruk. Siapakah yang membeli buah lebih banyak?
Cara Menyelesaikan Soal Perbandingan Pecahan dengan Perbandingan Tidak Langsung
Untuk menyelesaikan soal seperti ini, kita perlu mengubah kedua pecahan tersebut ke dalam bentuk pecahan yang memiliki penyebut yang sama. Dalam contoh ini, kita dapat mengubah 1/2 menjadi 2/4 dengan mengalikan pembilang dan penyebut dengan 2. Sekarang, kedua pecahan memiliki penyebut yang sama, yaitu 4. Dengan demikian, kita dapat membandingkan kedua pecahan tersebut: 2/4 lebih besar dari 1/4. Ini berarti Ibu membeli buah lebih banyak daripada Ayah.
Tabel Contoh Soal Perbandingan Pecahan dengan Perbandingan Tidak Langsung dan Penyelesaiannya, Contoh soal pecahan lebih besar lebih kecil
| Soal | Penyelesaian |
|---|---|
| Ani membeli 1/3 kg mangga, sedangkan Budi membeli 1/2 kg pisang. Siapakah yang membeli buah lebih banyak? | Kita perlu mengubah kedua pecahan tersebut ke dalam bentuk pecahan yang memiliki penyebut yang sama. Kita dapat mengubah 1/3 menjadi 2/6 dengan mengalikan pembilang dan penyebut dengan 2, dan mengubah 1/2 menjadi 3/6 dengan mengalikan pembilang dan penyebut dengan 3. Sekarang, kedua pecahan memiliki penyebut yang sama, yaitu 6. Dengan demikian, kita dapat membandingkan kedua pecahan tersebut: 3/6 lebih besar dari 2/6. Ini berarti Budi membeli buah lebih banyak daripada Ani. |
| Rina membeli 3/4 kg apel, sedangkan Dita membeli 1/2 kg jeruk. Siapakah yang membeli buah lebih banyak? | Kita perlu mengubah kedua pecahan tersebut ke dalam bentuk pecahan yang memiliki penyebut yang sama. Kita dapat mengubah 1/2 menjadi 2/4 dengan mengalikan pembilang dan penyebut dengan 2. Sekarang, kedua pecahan memiliki penyebut yang sama, yaitu 4. Dengan demikian, kita dapat membandingkan kedua pecahan tersebut: 3/4 lebih besar dari 2/4. Ini berarti Rina membeli buah lebih banyak daripada Dita. |
Soal Perbandingan Pecahan dengan Operasi Hitung
Soal perbandingan pecahan dengan operasi hitung mengharuskan kita untuk melakukan operasi hitung terlebih dahulu sebelum membandingkan pecahan yang dihasilkan. Soal ini menguji pemahaman kita tentang operasi hitung pecahan dan kemampuan kita dalam membandingkan pecahan.
Contoh Soal dan Penyelesaian
Sebagai contoh, kita dapat melihat soal berikut:
Tentukan pecahan yang lebih besar: 1/2 + 1/4 atau 3/4 – 1/8?
Untuk menyelesaikan soal ini, kita perlu melakukan operasi hitung pada kedua pecahan tersebut. Pertama, kita hitung 1/2 + 1/4. Untuk menjumlahkan pecahan, kita perlu memiliki penyebut yang sama. Kita bisa mengubah 1/2 menjadi 2/4. Sehingga, 1/2 + 1/4 = 2/4 + 1/4 = 3/4.
Selanjutnya, kita hitung 3/4 – 1/8. Kita perlu mencari penyebut persekutuan terkecil (PPK) dari 4 dan 8, yaitu 8. Kita bisa mengubah 3/4 menjadi 6/8. Sehingga, 3/4 – 1/8 = 6/8 – 1/8 = 5/8.
Sekarang, kita tinggal membandingkan 3/4 dan 5/8. Karena penyebutnya berbeda, kita perlu mengubahnya menjadi penyebut yang sama. Kita bisa mengubah 3/4 menjadi 6/8. Dengan demikian, 6/8 lebih besar daripada 5/8. Jadi, pecahan yang lebih besar adalah 1/2 + 1/4.
Tabel Contoh Soal dan Penyelesaian
| Soal | Penyelesaian |
|---|---|
| Tentukan pecahan yang lebih besar: 1/3 + 1/6 atau 2/3 – 1/9? | 1/3 + 1/6 = 2/6 + 1/6 = 3/6 = 1/2 2/3 – 1/9 = 6/9 – 1/9 = 5/9 1/2 lebih besar daripada 5/9. Jadi, pecahan yang lebih besar adalah 1/3 + 1/6. |
| Tentukan pecahan yang lebih kecil: 2/5 + 1/10 atau 3/5 – 1/5? | 2/5 + 1/10 = 4/10 + 1/10 = 5/10 = 1/2 3/5 – 1/5 = 2/5 1/2 lebih besar daripada 2/5. Jadi, pecahan yang lebih kecil adalah 3/5 – 1/5. |
Penutupan
Memahami perbandingan pecahan bukan hanya soal angka, tetapi juga tentang pemahaman yang lebih dalam tentang bagian-bagian yang membentuk keseluruhan. Dengan latihan yang cukup, kita dapat dengan mudah membandingkan pecahan dalam berbagai konteks, baik dalam soal matematika maupun dalam kehidupan sehari-hari.