Contoh soal peluang dan pembahasannya – Pernahkah kamu bertanya-tanya bagaimana peluangmu untuk mendapatkan nilai sempurna dalam ujian, atau kemungkinanmu untuk memenangkan lotre? Konsep peluang dalam matematika membantu kita memahami dan menghitung kemungkinan suatu kejadian terjadi. Dalam artikel ini, kita akan menjelajahi dunia peluang dengan mempelajari contoh soal dan pembahasannya. Mulai dari definisi peluang hingga berbagai jenis kejadian seperti kejadian bersyarat, kejadian bebas, dan kejadian gabungan, kita akan mengupas tuntas bagaimana menghitung peluang suatu kejadian dengan berbagai metode.
Dengan mempelajari contoh soal peluang dan pembahasannya, kamu akan memahami cara menggunakan rumus dan konsep peluang untuk menyelesaikan masalah sehari-hari. Artikel ini akan menjadi panduan yang komprehensif untuk memahami peluang dan mengasah kemampuanmu dalam menyelesaikan soal-soal peluang yang mungkin kamu temui di berbagai bidang, seperti statistika, probabilitas, dan ilmu data.
Pengertian Peluang
Peluang merupakan konsep dasar dalam matematika yang digunakan untuk mengukur kemungkinan terjadinya suatu kejadian. Dalam kehidupan sehari-hari, kita seringkali dihadapkan pada situasi yang melibatkan ketidakpastian, seperti saat melempar koin, memilih kartu dari setumpuk kartu, atau memprediksi cuaca. Peluang memberikan kerangka kerja untuk memahami dan mengkuantifikasi ketidakpastian ini.
Definisi Peluang
Peluang didefinisikan sebagai rasio antara jumlah hasil yang menguntungkan (kejadian yang ingin kita hitung) dengan jumlah total hasil yang mungkin terjadi. Dengan kata lain, peluang adalah ukuran kemungkinan suatu kejadian terjadi.
Sebagai contoh sederhana, perhatikan pelemparan sebuah dadu. Ada enam sisi pada dadu, yaitu angka 1, 2, 3, 4, 5, dan 6. Jika kita ingin menghitung peluang munculnya angka 3, maka jumlah hasil yang menguntungkan adalah 1 (sisi dadu yang menunjukkan angka 3), dan jumlah total hasil yang mungkin terjadi adalah 6 (semua sisi dadu).
Oleh karena itu, peluang munculnya angka 3 adalah 1/6.
Konsep Ruang Sampel dan Kejadian
Untuk memahami peluang lebih lanjut, kita perlu memahami konsep ruang sampel dan kejadian.
Ruang sampel adalah himpunan dari semua hasil yang mungkin terjadi dalam suatu percobaan.
Kejadian adalah subset dari ruang sampel, yaitu himpunan dari hasil yang kita minati.
Sebagai ilustrasi, perhatikan diagram Venn di bawah ini. Lingkaran besar mewakili ruang sampel, yang berisi semua hasil yang mungkin terjadi saat melempar koin. Lingkaran kecil mewakili kejadian “muncul sisi gambar”, yang merupakan subset dari ruang sampel.
Jenis-Jenis Peluang
Terdapat tiga jenis peluang yang umum digunakan dalam matematika, yaitu:
- Peluang Klasik: Peluang klasik dihitung berdasarkan asumsi bahwa semua hasil dalam ruang sampel memiliki kemungkinan yang sama untuk terjadi. Contohnya, peluang munculnya sisi gambar saat melempar koin adalah 1/2, karena ada dua hasil yang mungkin (gambar atau angka) dan keduanya memiliki kemungkinan yang sama untuk terjadi.
- Peluang Empiris: Peluang empiris dihitung berdasarkan hasil observasi atau eksperimen. Contohnya, jika kita melempar koin 100 kali dan sisi gambar muncul 55 kali, maka peluang empiris munculnya sisi gambar adalah 55/100 = 0,55.
- Peluang Subjektif: Peluang subjektif didasarkan pada keyakinan pribadi atau penilaian subjektif. Contohnya, seorang investor mungkin memperkirakan peluang keberhasilan suatu investasi berdasarkan pengalaman dan pengetahuan mereka.
Rumus Peluang
Peluang adalah konsep yang penting dalam matematika dan statistika, yang digunakan untuk mengukur kemungkinan terjadinya suatu kejadian. Rumus peluang adalah alat yang digunakan untuk menghitung probabilitas dari suatu kejadian, yang didefinisikan sebagai perbandingan antara jumlah kejadian yang diinginkan dengan jumlah total kejadian yang mungkin terjadi.
Rumus Dasar Peluang
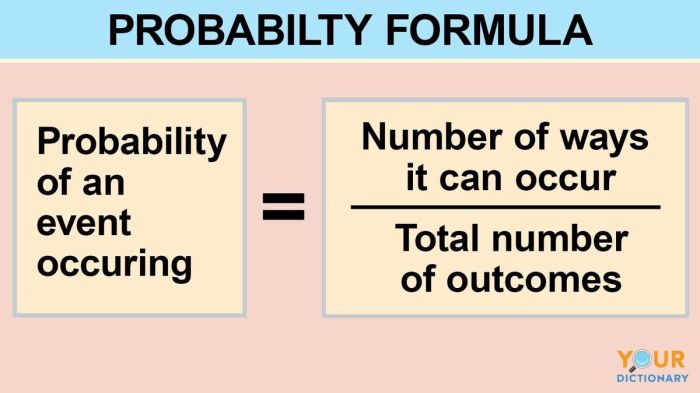
Rumus dasar perhitungan peluang dapat dinyatakan sebagai berikut:
Peluang (Kejadian) = Jumlah Kejadian yang Diinginkan / Jumlah Total Kejadian yang Mungkin Terjadi
Misalnya, jika kita melempar sebuah dadu, peluang mendapatkan angka 6 adalah 1/6. Ini karena terdapat satu kejadian yang diinginkan (mendapatkan angka 6) dan enam kejadian yang mungkin terjadi (mendapatkan angka 1, 2, 3, 4, 5, atau 6).
Peluang Kejadian Komplemen
Kejadian komplemen adalah kejadian yang tidak terjadi, yaitu kebalikan dari kejadian yang diinginkan. Peluang kejadian komplemen dapat dihitung dengan mengurangi peluang kejadian dari 1.
Peluang (Komplemen Kejadian) = 1 – Peluang (Kejadian)
Misalnya, jika peluang mendapatkan angka genap pada pelemparan dadu adalah 1/2, maka peluang mendapatkan angka ganjil adalah 1 – 1/2 = 1/2.
Rumus Perhitungan Peluang untuk Berbagai Jenis Kejadian
Berikut adalah tabel yang berisi rumus perhitungan peluang untuk berbagai jenis kejadian:
| Jenis Kejadian | Rumus |
|---|---|
| Kejadian Gabungan (A atau B) | P(A ∪ B) = P(A) + P(B) – P(A ∩ B) |
| Kejadian Irisan (A dan B) | P(A ∩ B) = P(A) * P(B|A) |
| Kejadian Bersyarat (B, diberikan A) | P(B|A) = P(A ∩ B) / P(A) |
Rumus-rumus ini membantu kita untuk menghitung peluang kejadian yang lebih kompleks, seperti peluang mendapatkan kartu As atau kartu King dalam satu kali pengambilan kartu dari setumpuk kartu.
Contoh Soal Peluang Dasar
Peluang merupakan konsep dasar dalam matematika yang menjelaskan kemungkinan suatu kejadian terjadi. Konsep peluang sangat berguna dalam kehidupan sehari-hari, mulai dari perhitungan kemungkinan memenangkan undian hingga memprediksi hasil suatu eksperimen.
Untuk memahami konsep peluang dengan lebih baik, mari kita bahas beberapa contoh soal peluang dasar yang melibatkan dadu dan kartu remi.
Contoh Soal Peluang dengan Dadu
Dalam contoh soal peluang dengan dadu, kita akan membahas tentang kemungkinan munculnya sisi tertentu saat sebuah dadu dilempar.
Misalnya, kita ingin menghitung peluang munculnya sisi 6 pada pelemparan sebuah dadu.
Langkah-langkah untuk menghitung peluang ini adalah:
- Tentukan jumlah sisi dadu, yaitu 6.
- Tentukan jumlah sisi yang diinginkan, yaitu 1 (sisi 6).
- Hitung peluang dengan rumus: Peluang = (Jumlah sisi yang diinginkan) / (Jumlah sisi total) = 1/6.
Jadi, peluang munculnya sisi 6 pada pelemparan sebuah dadu adalah 1/6.
Contoh Soal Peluang dengan Kartu Remi
Dalam contoh soal peluang dengan kartu remi, kita akan membahas tentang kemungkinan munculnya kartu tertentu saat sebuah kartu di ambil dari setumpuk kartu remi.
Misalnya, kita ingin menghitung peluang munculnya kartu As saat sebuah kartu di ambil dari setumpuk kartu remi.
Langkah-langkah untuk menghitung peluang ini adalah:
- Tentukan jumlah total kartu dalam setumpuk kartu remi, yaitu 52.
- Tentukan jumlah kartu As dalam setumpuk kartu remi, yaitu 4.
- Hitung peluang dengan rumus: Peluang = (Jumlah kartu As) / (Jumlah total kartu) = 4/52 = 1/13.
Jadi, peluang munculnya kartu As saat sebuah kartu di ambil dari setumpuk kartu remi adalah 1/13.
Langkah-langkah Penyelesaian Soal Peluang Dasar
Untuk menyelesaikan soal peluang dasar, langkah-langkah yang perlu dilakukan adalah:
- Tentukan ruang sampel, yaitu semua kemungkinan hasil yang mungkin terjadi dalam suatu percobaan.
- Tentukan kejadian yang ingin dihitung peluangnya.
- Hitung jumlah elemen dalam kejadian tersebut.
- Hitung peluang dengan rumus: Peluang = (Jumlah elemen dalam kejadian) / (Jumlah elemen dalam ruang sampel).
Sebagai contoh, kita ingin menghitung peluang munculnya sisi genap pada pelemparan sebuah dadu.
- Ruang sampel: 1, 2, 3, 4, 5, 6
- Kejadian: Munculnya sisi genap
- Jumlah elemen dalam kejadian: 3 (sisi 2, 4, dan 6)
- Peluang: 3/6 = 1/2
Jadi, peluang munculnya sisi genap pada pelemparan sebuah dadu adalah 1/2.
Peluang Bersyarat
Peluang bersyarat merupakan konsep penting dalam teori peluang yang mempelajari peluang suatu kejadian terjadi, dengan asumsi bahwa kejadian lain telah terjadi sebelumnya. Konsep ini sering kali diterapkan dalam berbagai bidang seperti statistik, ilmu data, dan pengambilan keputusan. Misalnya, dalam dunia bisnis, peluang bersyarat dapat digunakan untuk memprediksi probabilitas keberhasilan suatu kampanye pemasaran setelah mengetahui perilaku konsumen sebelumnya.
Pengertian Peluang Bersyarat
Peluang bersyarat didefinisikan sebagai peluang suatu kejadian terjadi, dengan asumsi bahwa kejadian lain yang berkaitan dengannya telah terjadi. Dalam kata lain, peluang bersyarat adalah peluang kejadian A terjadi, dengan syarat kejadian B telah terjadi.
Rumus Peluang Bersyarat
Rumus perhitungan peluang bersyarat adalah sebagai berikut:
P(A|B) = P(A∩B) / P(B)
Keterangan:
- P(A|B) adalah peluang kejadian A terjadi, dengan syarat kejadian B telah terjadi.
- P(A∩B) adalah peluang kejadian A dan B terjadi bersamaan.
- P(B) adalah peluang kejadian B terjadi.
Rumus ini menyatakan bahwa peluang bersyarat kejadian A dengan syarat B terjadi sama dengan peluang kejadian A dan B terjadi bersamaan dibagi dengan peluang kejadian B.
Contoh Soal Peluang Bersyarat
Misalkan sebuah kotak berisi 5 bola merah dan 3 bola biru. Kita ingin mengetahui peluang mengambil bola merah dari kotak tersebut, dengan syarat bahwa bola pertama yang diambil adalah bola biru dan tidak dikembalikan ke dalam kotak.
Pertama, kita tentukan kejadian-kejadian yang terlibat:
- Kejadian A: Mengambil bola merah.
- Kejadian B: Mengambil bola biru pada pengambilan pertama.
Kemudian, kita hitung peluang masing-masing kejadian:
- P(B) = 3/8 (peluang mengambil bola biru pada pengambilan pertama).
- P(A∩B) = (3/8) * (5/7) = 15/56 (peluang mengambil bola biru pada pengambilan pertama dan bola merah pada pengambilan kedua).
Sekarang, kita dapat menghitung peluang bersyarat mengambil bola merah, dengan syarat bola pertama yang diambil adalah bola biru:
P(A|B) = P(A∩B) / P(B) = (15/56) / (3/8) = 5/7.
Jadi, peluang mengambil bola merah, dengan syarat bola pertama yang diambil adalah bola biru, adalah 5/7.
Hubungan Peluang Bersyarat, Peluang Kejadian, dan Peluang Kejadian Bersyarat
Tabel berikut menunjukkan hubungan antara peluang bersyarat, peluang kejadian, dan peluang kejadian bersyarat:
| Kejadian | Peluang Kejadian | Peluang Kejadian Bersyarat | Peluang Bersyarat |
|---|---|---|---|
| A | P(A) | P(A|B) | P(B|A) |
| B | P(B) | P(B|A) | P(A|B) |
Dari tabel tersebut, dapat dilihat bahwa peluang bersyarat merupakan hubungan timbal balik antara dua kejadian. Peluang bersyarat kejadian A dengan syarat B terjadi, yaitu P(A|B), berhubungan dengan peluang bersyarat kejadian B dengan syarat A terjadi, yaitu P(B|A).
Peluang Bersyarat
Peluang bersyarat adalah peluang terjadinya suatu kejadian, dengan syarat kejadian lain sudah terjadi terlebih dahulu. Konsep ini penting dalam berbagai bidang seperti statistik, probabilitas, dan pengambilan keputusan. Untuk memahami konsep ini lebih lanjut, mari kita bahas melalui contoh soal dan penyelesaiannya.
Contoh Soal Peluang Bersyarat
Misalnya, dalam sebuah kelas terdapat 20 siswa. 12 siswa menyukai matematika, 10 siswa menyukai fisika, dan 6 siswa menyukai keduanya. Jika dipilih seorang siswa secara acak, berapakah peluang siswa tersebut menyukai matematika, dengan syarat ia menyukai fisika?
Langkah-Langkah Penyelesaian Soal Peluang Bersyarat
Untuk menyelesaikan soal peluang bersyarat, kita dapat mengikuti langkah-langkah berikut:
- Tentukan kejadian A dan kejadian B yang ingin dihitung peluangnya. Dalam contoh soal, kejadian A adalah siswa menyukai matematika, dan kejadian B adalah siswa menyukai fisika.
- Tentukan kejadian B yang sudah terjadi terlebih dahulu. Dalam contoh soal, kejadian B (siswa menyukai fisika) sudah terjadi terlebih dahulu.
- Hitung peluang kejadian A dengan syarat kejadian B sudah terjadi. Peluang ini disebut peluang bersyarat dan dilambangkan dengan P(A|B). Dalam contoh soal, P(A|B) adalah peluang siswa menyukai matematika, dengan syarat ia menyukai fisika.
- Rumus untuk menghitung peluang bersyarat adalah:
P(A|B) = P(A dan B) / P(B)
Keterangan:
- P(A dan B) adalah peluang kejadian A dan B terjadi bersamaan.
- P(B) adalah peluang kejadian B terjadi.
Berdasarkan contoh soal, kita dapat menghitung P(A|B) sebagai berikut:
- P(A dan B) = 6/20 (karena 6 siswa menyukai matematika dan fisika)
- P(B) = 10/20 (karena 10 siswa menyukai fisika)
- P(A|B) = (6/20) / (10/20) = 6/10 = 0,6
Jadi, peluang siswa tersebut menyukai matematika, dengan syarat ia menyukai fisika adalah 0,6 atau 60%.
Tabel Hubungan Peluang
Tabel berikut menunjukkan hubungan antara peluang bersyarat, peluang kejadian, dan peluang kejadian bersyarat dalam contoh soal:
| Kejadian | Peluang | Peluang Bersyarat |
|---|---|---|
| Siswa menyukai matematika (A) | 12/20 = 0,6 | P(A|B) = 0,6 |
| Siswa menyukai fisika (B) | 10/20 = 0,5 | P(B|A) = 6/12 = 0,5 |
| Siswa menyukai matematika dan fisika (A dan B) | 6/20 = 0,3 | – |
Dari tabel tersebut, kita dapat melihat bahwa peluang bersyarat P(A|B) = 0,6 berbeda dengan peluang kejadian A = 0,6. Hal ini menunjukkan bahwa kejadian B (siswa menyukai fisika) memengaruhi peluang kejadian A (siswa menyukai matematika).
Peluang Kejadian Bebas
Dalam teori peluang, memahami konsep kejadian bebas sangat penting. Kejadian bebas merupakan kejadian yang tidak saling memengaruhi. Artinya, hasil dari satu kejadian tidak akan mempengaruhi hasil kejadian lainnya. Misalnya, saat melempar koin dua kali, hasil lemparan pertama tidak akan mempengaruhi hasil lemparan kedua. Pada artikel ini, kita akan menjelajahi konsep peluang kejadian bebas dengan contoh soal dan rumus perhitungannya.
Pengertian Kejadian Bebas
Kejadian bebas adalah kejadian yang tidak saling memengaruhi. Artinya, hasil dari satu kejadian tidak akan mempengaruhi hasil kejadian lainnya. Contohnya, saat melempar dadu dan koin secara bersamaan, hasil lemparan dadu tidak akan mempengaruhi hasil lemparan koin.
Rumus Perhitungan Peluang Kejadian Bebas
Peluang kejadian bebas dihitung dengan mengalikan peluang setiap kejadian. Rumusnya adalah:
P(A dan B) = P(A) x P(B)
Dimana:
- P(A dan B) adalah peluang kejadian A dan B terjadi secara bersamaan.
- P(A) adalah peluang kejadian A terjadi.
- P(B) adalah peluang kejadian B terjadi.
Contoh Soal Peluang Kejadian Bebas
Berikut adalah contoh soal untuk memahami konsep peluang kejadian bebas:
Sebuah kotak berisi 5 bola merah dan 3 bola biru. Dua bola diambil secara acak dan berturut-turut tanpa pengembalian. Hitunglah peluang terambilnya bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua.
Penyelesaian:
Kejadian terambilnya bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua merupakan kejadian bebas karena pengambilan dilakukan tanpa pengembalian.
Peluang terambilnya bola merah pada pengambilan pertama adalah 5/8 (karena ada 5 bola merah dari total 8 bola).
Setelah terambilnya bola merah pertama, sisa bola di dalam kotak adalah 4 bola merah dan 3 bola biru (total 7 bola). Peluang terambilnya bola biru pada pengambilan kedua adalah 3/7.
Maka, peluang terambilnya bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua adalah:
P(merah dan biru) = P(merah) x P(biru) = (5/8) x (3/7) = 15/56
Perbedaan Kejadian Bebas dan Kejadian Tidak Bebas
Berikut adalah tabel yang menunjukkan perbedaan antara kejadian bebas dan kejadian tidak bebas:
| Karakteristik | Kejadian Bebas | Kejadian Tidak Bebas |
|---|---|---|
| Definisi | Kejadian yang tidak saling memengaruhi | Kejadian yang saling memengaruhi |
| Contoh | Melempar koin dua kali | Mengambil kartu dari setumpuk kartu tanpa pengembalian |
| Rumus Perhitungan | P(A dan B) = P(A) x P(B) | P(A dan B) = P(A) x P(B|A) |
Soal Peluang Kejadian Bebas: Contoh Soal Peluang Dan Pembahasannya
Peluang kejadian bebas merupakan konsep penting dalam teori probabilitas. Kejadian bebas adalah kejadian yang tidak saling memengaruhi satu sama lain. Artinya, hasil dari satu kejadian tidak akan mempengaruhi hasil dari kejadian lainnya. Untuk memahami konsep ini, kita akan membahas contoh soal cerita, langkah-langkah penyelesaian, dan tabel perbedaan antara kejadian bebas dan kejadian tidak bebas.
Contoh Soal Cerita Peluang Kejadian Bebas
Misalkan terdapat sebuah kotak berisi 5 bola merah dan 3 bola biru. Seorang anak mengambil satu bola secara acak dari kotak tersebut, lalu dikembalikan. Setelah itu, anak tersebut mengambil satu bola lagi secara acak. Tentukan peluang anak tersebut mengambil bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua.
Contoh soal peluang dan pembahasannya bisa jadi rumit, tapi bisa dibantu dengan memahami konsep dasar. Misalnya, kamu bisa coba hitung peluang munculnya sisi gambar pada pelemparan koin. Nah, untuk soal bahasa Inggris, kamu bisa belajar dari contoh soal matching seperti yang ada di contoh soal matching bahasa inggris.
Sama seperti soal peluang, contoh soal matching juga membantu kamu memahami dan mempraktikkan materi. Jadi, jangan ragu untuk latihan dan memahami konsepnya agar kamu bisa menguasai materi dengan lebih baik!
Langkah-langkah Penyelesaian Soal Peluang Kejadian Bebas
Untuk menyelesaikan soal peluang kejadian bebas, kita dapat menggunakan rumus berikut:
P(A dan B) = P(A) x P(B)
Dimana:
- P(A dan B) adalah peluang kejadian A dan kejadian B terjadi bersamaan.
- P(A) adalah peluang kejadian A terjadi.
- P(B) adalah peluang kejadian B terjadi.
Dalam contoh soal cerita di atas, kejadian A adalah mengambil bola merah pada pengambilan pertama, dan kejadian B adalah mengambil bola biru pada pengambilan kedua. Untuk menghitung peluangnya, kita dapat mengikuti langkah-langkah berikut:
- Hitung peluang kejadian A (mengambil bola merah pada pengambilan pertama). Peluang ini adalah 5/8, karena terdapat 5 bola merah dari total 8 bola.
- Hitung peluang kejadian B (mengambil bola biru pada pengambilan kedua). Karena bola pertama dikembalikan, jumlah bola di dalam kotak tetap sama. Peluang mengambil bola biru adalah 3/8.
- Hitung peluang kejadian A dan B terjadi bersamaan. P(A dan B) = P(A) x P(B) = (5/8) x (3/8) = 15/64.
Jadi, peluang anak tersebut mengambil bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua adalah 15/64.
Perbedaan Kejadian Bebas dan Kejadian Tidak Bebas
| Karakteristik | Kejadian Bebas | Kejadian Tidak Bebas |
|---|---|---|
| Definisi | Kejadian yang tidak saling memengaruhi satu sama lain. | Kejadian yang saling memengaruhi satu sama lain. |
| Contoh | Melempar koin dan melempar dadu. | Mengambil kartu dari satu set kartu tanpa pengembalian. |
| Rumus | P(A dan B) = P(A) x P(B) | P(A dan B) = P(A) x P(B|A) |
Peluang Kejadian Gabungan
Peluang kejadian gabungan adalah peluang terjadinya salah satu atau kedua kejadian dari dua kejadian atau lebih. Konsep ini sangat berguna dalam berbagai bidang, seperti statistik, probabilitas, dan pengambilan keputusan.
Pengertian Peluang Kejadian Gabungan, Contoh soal peluang dan pembahasannya
Peluang kejadian gabungan adalah peluang terjadinya salah satu atau kedua kejadian dari dua kejadian atau lebih. Misalnya, jika kita melempar sebuah dadu, peluang mendapatkan angka genap atau angka lebih besar dari 4 adalah peluang kejadian gabungan. Kejadian pertama adalah mendapatkan angka genap, dan kejadian kedua adalah mendapatkan angka lebih besar dari 4.
Rumus Peluang Kejadian Gabungan
Rumus peluang kejadian gabungan adalah sebagai berikut:
P(A U B) = P(A) + P(B) – P(A ∩ B)
di mana:
- P(A U B) adalah peluang kejadian A atau kejadian B terjadi.
- P(A) adalah peluang kejadian A terjadi.
- P(B) adalah peluang kejadian B terjadi.
- P(A ∩ B) adalah peluang kejadian A dan kejadian B terjadi bersamaan.
Contoh Soal Peluang Kejadian Gabungan
Misalnya, kita memiliki sebuah kotak berisi 5 bola merah, 3 bola biru, dan 2 bola hijau. Kita mengambil satu bola secara acak dari kotak tersebut. Berapakah peluang kita mendapatkan bola merah atau bola biru?
Penyelesaian
Pertama, kita hitung peluang mendapatkan bola merah:
P(Merah) = 5 / 10 = 1/2
Kemudian, kita hitung peluang mendapatkan bola biru:
P(Biru) = 3 / 10
Selanjutnya, kita hitung peluang mendapatkan bola merah dan bola biru bersamaan (yang tidak mungkin terjadi karena kita hanya mengambil satu bola):
P(Merah ∩ Biru) = 0
Sekarang, kita dapat menghitung peluang mendapatkan bola merah atau bola biru menggunakan rumus peluang kejadian gabungan:
P(Merah U Biru) = P(Merah) + P(Biru) – P(Merah ∩ Biru) = 1/2 + 3/10 – 0 = 8/10 = 4/5
Jadi, peluang mendapatkan bola merah atau bola biru adalah 4/5.
Perbedaan Kejadian Gabungan dan Kejadian Irisan
Berikut adalah tabel yang menunjukkan perbedaan antara kejadian gabungan dan kejadian irisan:
| Karakteristik | Kejadian Gabungan | Kejadian Irisan |
|---|---|---|
| Definisi | Terjadinya salah satu atau kedua kejadian dari dua kejadian atau lebih. | Terjadinya kedua kejadian dari dua kejadian atau lebih. |
| Simbol | A U B | A ∩ B |
| Rumus | P(A U B) = P(A) + P(B) – P(A ∩ B) | P(A ∩ B) = P(A) * P(B|A) |
| Contoh | Mendapatkan angka genap atau angka lebih besar dari 4 saat melempar dadu. | Mendapatkan angka genap dan angka lebih besar dari 4 saat melempar dadu (tidak mungkin terjadi). |
Soal Peluang Kejadian Gabungan
Peluang kejadian gabungan adalah peluang terjadinya setidaknya satu dari dua kejadian atau lebih. Kejadian gabungan dilambangkan dengan simbol “∪” atau “atau”. Untuk memahami konsep ini, mari kita bahas contoh soal berikut:
Contoh Soal Peluang Kejadian Gabungan
Sebuah kotak berisi 5 bola merah, 3 bola biru, dan 2 bola hijau. Jika diambil 1 bola secara acak, tentukan peluang terambilnya bola merah atau bola biru!
Langkah-langkah Penyelesaian Soal Peluang Kejadian Gabungan
Untuk menyelesaikan soal peluang kejadian gabungan, kita dapat mengikuti langkah-langkah berikut:
- Tentukan kejadian-kejadian yang terlibat dalam soal. Dalam contoh soal di atas, kejadian yang terlibat adalah terambilnya bola merah dan terambilnya bola biru.
- Tentukan peluang masing-masing kejadian. Peluang terambilnya bola merah adalah 5/10, sedangkan peluang terambilnya bola biru adalah 3/10.
- Hitung peluang kejadian gabungan dengan menggunakan rumus:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Dimana:
* P(A ∪ B) adalah peluang kejadian A atau kejadian B
* P(A) adalah peluang kejadian A
* P(B) adalah peluang kejadian B
* P(A ∩ B) adalah peluang kejadian A dan kejadian B - Dalam contoh soal, P(A ∩ B) = 0 karena tidak mungkin terambil bola merah dan biru secara bersamaan dalam satu pengambilan.
- Jadi, peluang terambilnya bola merah atau bola biru adalah:
P(merah ∪ biru) = P(merah) + P(biru) – P(merah ∩ biru)
= 5/10 + 3/10 – 0
= 8/10
= 4/5
Perbedaan Kejadian Gabungan dan Kejadian Irisan
Berikut tabel yang menunjukkan perbedaan antara kejadian gabungan dan kejadian irisan:
| Aspek | Kejadian Gabungan | Kejadian Irisan |
|---|---|---|
| Definisi | Terjadinya setidaknya satu dari dua kejadian atau lebih | Terjadinya kedua kejadian atau lebih secara bersamaan |
| Simbol | ∪ atau “atau” | ∩ atau “dan” |
| Contoh | Terambilnya bola merah atau bola biru | Terambilnya bola merah dan bola biru |
| Rumus | P(A ∪ B) = P(A) + P(B) – P(A ∩ B) | P(A ∩ B) = P(A) * P(B|A) |
Akhir Kata
Memahami konsep peluang dan cara menghitungnya adalah keterampilan yang sangat berguna dalam berbagai bidang kehidupan. Dengan mempelajari contoh soal dan pembahasannya, kita dapat mengasah kemampuan analitis dan berpikir kritis untuk menghadapi berbagai situasi yang melibatkan probabilitas. Jadi, jangan ragu untuk menjelajahi lebih lanjut tentang peluang dan mengaplikasikannya dalam kehidupan sehari-hari!





