Contoh soal peluang kejadian majemuk – Pernahkah Anda bertanya-tanya bagaimana peluang mendapatkan dua sisi gambar saat melempar koin dua kali? Atau peluang mendapatkan kartu As dan King dari satu set kartu remi? Itulah contoh nyata dari peluang kejadian majemuk, yaitu peluang terjadinya dua atau lebih kejadian secara bersamaan. Dalam artikel ini, kita akan menjelajahi dunia menarik peluang kejadian majemuk, mulai dari pengertian hingga contoh soal dan aplikasinya dalam kehidupan sehari-hari.
Peluang kejadian majemuk melibatkan perhitungan probabilitas dari dua atau lebih kejadian yang terjadi secara bersamaan. Kita akan mempelajari berbagai jenis kejadian majemuk, seperti kejadian saling bebas dan saling tidak bebas, serta bagaimana menghitung peluangnya menggunakan rumus yang tepat. Siap untuk mengungkap rahasia di balik kejadian-kejadian yang terjadi bersamaan?
Pengertian Kejadian Majemuk
Dalam dunia peluang, kita sering kali berhadapan dengan kejadian yang terdiri dari lebih dari satu kejadian tunggal. Kejadian-kejadian ini saling berhubungan dan hasil akhirnya ditentukan oleh gabungan dari semua kejadian tersebut. Kejadian yang terdiri dari dua atau lebih kejadian tunggal yang terjadi secara bersamaan atau berurutan disebut sebagai kejadian majemuk.
Contoh Kejadian Majemuk dalam Kehidupan Sehari-hari
Kejadian majemuk mudah dijumpai dalam kehidupan sehari-hari. Berikut beberapa contohnya:
- Memilih baju dan celana untuk dipakai: Kejadian ini terdiri dari dua kejadian tunggal, yaitu memilih baju dan memilih celana. Hasil akhirnya adalah kombinasi baju dan celana yang dipilih.
- Melempar dadu dua kali: Kejadian ini terdiri dari dua kejadian tunggal, yaitu melempar dadu pertama dan melempar dadu kedua. Hasil akhirnya adalah kombinasi angka yang muncul pada kedua dadu tersebut.
- Memilih kartu As dan kartu King dari satu set kartu remi: Kejadian ini terdiri dari dua kejadian tunggal, yaitu memilih kartu As dan memilih kartu King. Hasil akhirnya adalah mendapatkan kedua kartu tersebut.
Perbedaan Kejadian Majemuk dan Kejadian Tunggal
Untuk lebih memahami perbedaan antara kejadian majemuk dan kejadian tunggal, perhatikan tabel berikut:
| Aspek | Kejadian Tunggal | Kejadian Majemuk |
|---|---|---|
| Definisi | Kejadian yang terjadi sendiri dan tidak bergantung pada kejadian lain. | Kejadian yang terdiri dari dua atau lebih kejadian tunggal yang terjadi secara bersamaan atau berurutan. |
| Contoh | Melempar koin sekali dan mendapatkan sisi kepala. | Melempar koin dua kali dan mendapatkan sisi kepala pada kedua lemparan. |
| Rumus Peluang | P(A) = n(A) / n(S) | P(A dan B) = P(A) x P(B) (jika kejadian independen) |
Jenis-Jenis Kejadian Majemuk
Kejadian majemuk merupakan gabungan dari dua atau lebih kejadian tunggal. Kejadian-kejadian ini dapat saling berhubungan atau tidak, dan hal ini menentukan jenis kejadian majemuk yang terjadi.
Berdasarkan hubungan antar kejadian, kejadian majemuk dapat dibedakan menjadi dua jenis, yaitu kejadian majemuk saling bebas dan kejadian majemuk saling tidak bebas. Berikut penjelasan lebih detailnya:
Kejadian Majemuk Saling Bebas
Kejadian majemuk saling bebas adalah kejadian majemuk di mana terjadinya satu kejadian tidak memengaruhi peluang terjadinya kejadian lainnya. Artinya, peluang terjadinya suatu kejadian tetap sama, terlepas dari apakah kejadian lain telah terjadi atau belum.
- Contoh: Membalikkan koin dua kali. Peluang mendapatkan sisi gambar pada lemparan pertama tidak memengaruhi peluang mendapatkan sisi gambar pada lemparan kedua. Peluang mendapatkan sisi gambar pada setiap lemparan tetap 1/2, terlepas dari hasil lemparan sebelumnya.
Kejadian Majemuk Saling Tidak Bebas
Kejadian majemuk saling tidak bebas adalah kejadian majemuk di mana terjadinya satu kejadian memengaruhi peluang terjadinya kejadian lainnya. Artinya, peluang terjadinya suatu kejadian berubah, tergantung pada apakah kejadian lain telah terjadi atau belum.
Contoh soal peluang kejadian majemuk bisa dibilang mirip dengan konsep perkalian dalam aljabar. Misalnya, peluang mendapatkan sisi kepala pada pelemparan koin pertama dan sisi gambar pada pelemparan koin kedua. Nah, untuk memahami lebih lanjut tentang perkalian dalam aljabar, kamu bisa cek contoh soal-soal di contoh soal perkalian aljabar kelas 7.
Setelah kamu memahami konsep perkalian aljabar, kamu akan lebih mudah memahami cara menghitung peluang kejadian majemuk.
- Contoh: Mengambil dua kartu secara berurutan dari satu set kartu remi tanpa pengembalian. Peluang mengambil kartu As pada pengambilan pertama adalah 4/52. Setelah mengambil kartu As pada pengambilan pertama, peluang mengambil kartu As pada pengambilan kedua menjadi 3/51, karena jumlah kartu As berkurang dan total kartu juga berkurang.
Rumus Peluang Kejadian Majemuk
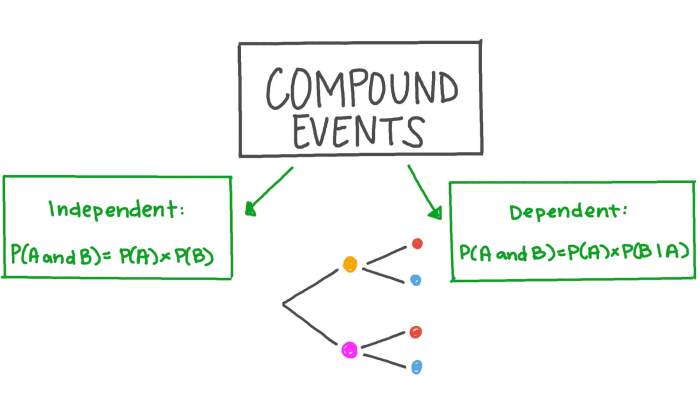
Kejadian majemuk merupakan gabungan dari dua atau lebih kejadian. Peluang kejadian majemuk dapat dihitung dengan menggunakan rumus yang berbeda tergantung pada apakah kejadian-kejadian tersebut saling bebas atau saling tidak bebas.
Kejadian Majemuk Saling Bebas
Kejadian majemuk saling bebas terjadi ketika peluang terjadinya satu kejadian tidak memengaruhi peluang terjadinya kejadian lainnya. Contohnya, melempar koin dua kali, hasil lemparan pertama tidak memengaruhi hasil lemparan kedua.
Rumus untuk menghitung peluang kejadian majemuk saling bebas adalah:
P(A dan B) = P(A) x P(B)
Dimana:
- P(A dan B) adalah peluang kejadian A dan B terjadi bersamaan
- P(A) adalah peluang kejadian A terjadi
- P(B) adalah peluang kejadian B terjadi
Kejadian Majemuk Saling Tidak Bebas
Kejadian majemuk saling tidak bebas terjadi ketika peluang terjadinya satu kejadian memengaruhi peluang terjadinya kejadian lainnya. Contohnya, mengambil dua kartu dari satu set kartu tanpa pengembalian, peluang mengambil kartu as pada pengambilan kedua bergantung pada kartu yang diambil pada pengambilan pertama.
Rumus untuk menghitung peluang kejadian majemuk saling tidak bebas adalah:
P(A dan B) = P(A) x P(B|A)
Dimana:
- P(A dan B) adalah peluang kejadian A dan B terjadi bersamaan
- P(A) adalah peluang kejadian A terjadi
- P(B|A) adalah peluang kejadian B terjadi dengan syarat kejadian A sudah terjadi
Penerapan Rumus dalam Soal, Contoh soal peluang kejadian majemuk
Berikut adalah contoh soal untuk menerapkan rumus peluang kejadian majemuk:
Misalkan sebuah kotak berisi 5 bola merah dan 3 bola biru. Diambil 2 bola secara acak tanpa pengembalian. Hitunglah peluang terambilnya 2 bola merah.
Kejadian ini merupakan kejadian majemuk saling tidak bebas karena pengambilan bola pertama memengaruhi peluang pengambilan bola kedua.
Misalkan A adalah kejadian terambilnya bola merah pada pengambilan pertama dan B adalah kejadian terambilnya bola merah pada pengambilan kedua.
Maka, P(A) = 5/8 (peluang terambilnya bola merah pada pengambilan pertama)
P(B|A) = 4/7 (peluang terambilnya bola merah pada pengambilan kedua dengan syarat bola merah sudah terambil pada pengambilan pertama)
Sehingga, P(A dan B) = P(A) x P(B|A) = (5/8) x (4/7) = 5/14
Jadi, peluang terambilnya 2 bola merah adalah 5/14.
Ulasan Penutup: Contoh Soal Peluang Kejadian Majemuk
Memahami konsep peluang kejadian majemuk tidak hanya penting dalam matematika dan statistik, tetapi juga dalam kehidupan sehari-hari. Dari membuat keputusan bisnis hingga memprediksi hasil pertandingan olahraga, konsep ini membantu kita menganalisis kemungkinan dan mengambil keputusan yang lebih baik. Jadi, mari kita tingkatkan pemahaman kita tentang peluang kejadian majemuk dan gunakannya untuk menghadapi tantangan yang ada di depan.




