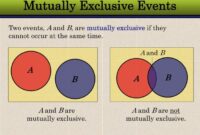
Contoh soal peluang kejadian tidak saling bebas – Pernahkah Anda bertanya-tanya bagaimana peluang suatu kejadian dipengaruhi oleh kejadian lain? Dalam dunia peluang, konsep kejadian tidak saling bebas menawarkan pemahaman yang menarik tentang bagaimana dua kejadian saling terkait dan memengaruhi probabilitas satu sama lain. Misalnya, jika Anda mengambil kartu dari setumpuk kartu, peluang mengambil kartu as akan berubah setelah Anda mengambil kartu pertama. Nah, itulah contoh sederhana dari kejadian tidak saling bebas, di mana kejadian pertama memengaruhi kejadian kedua.
Artikel ini akan membahas konsep kejadian tidak saling bebas, mulai dari pengertian hingga penerapannya dalam berbagai konteks. Kita akan menjelajahi rumus, contoh soal, dan berbagai aplikasi dalam kehidupan nyata untuk membantu Anda memahami dengan lebih baik bagaimana peluang kejadian tidak saling bebas bekerja.
Pengertian Kejadian Tidak Saling Bebas
Dalam teori peluang, memahami konsep kejadian saling bebas dan tidak saling bebas sangat penting untuk menghitung probabilitas kejadian kompleks. Kejadian saling bebas adalah kejadian yang tidak saling memengaruhi, sementara kejadian tidak saling bebas adalah kejadian yang saling memengaruhi. Artikel ini akan membahas lebih dalam mengenai pengertian kejadian tidak saling bebas dan memberikan contoh konkretnya.
Pengertian Kejadian Tidak Saling Bebas
Kejadian tidak saling bebas (dependent events) dalam teori peluang merujuk pada kejadian di mana terjadinya satu kejadian memengaruhi probabilitas terjadinya kejadian lainnya. Artinya, hasil dari satu kejadian dapat mengubah probabilitas kejadian berikutnya.
Contoh Kejadian Tidak Saling Bebas
Contoh konkret kejadian tidak saling bebas dapat kita temui dalam kehidupan sehari-hari. Misalnya:
- Mengambil Dua Bola dari Sebuah Wadah Tanpa Pengembalian: Bayangkan sebuah wadah berisi 5 bola merah dan 3 bola biru. Jika kita mengambil satu bola merah dari wadah tersebut tanpa mengembalikannya, maka probabilitas mengambil bola merah lagi pada pengambilan kedua akan berubah. Ini karena jumlah bola merah di dalam wadah telah berkurang, dan jumlah total bola juga berkurang.
- Menghidupkan Lampu: Bayangkan kamu memiliki dua lampu. Jika lampu pertama menyala, probabilitas lampu kedua menyala akan berubah. Hal ini karena kedua lampu mungkin terhubung ke sumber listrik yang sama.
Perbedaan Kejadian Saling Bebas dan Tidak Saling Bebas
Untuk lebih memahami perbedaan antara kejadian saling bebas dan tidak saling bebas, perhatikan tabel berikut:
| Ciri | Kejadian Saling Bebas | Kejadian Tidak Saling Bebas |
|---|---|---|
| Pengertian | Kejadian yang tidak saling memengaruhi | Kejadian yang saling memengaruhi |
| Probabilitas | Probabilitas satu kejadian tidak memengaruhi probabilitas kejadian lainnya | Probabilitas satu kejadian memengaruhi probabilitas kejadian lainnya |
| Contoh | Membalik koin dua kali. Hasil lemparan pertama tidak memengaruhi hasil lemparan kedua. | Mengambil kartu dari satu set kartu tanpa pengembalian. Mengambil kartu pertama memengaruhi probabilitas kartu kedua. |
Rumus Peluang Kejadian Tidak Saling Bebas
Kejadian tidak saling bebas merupakan situasi di mana kejadian satu mempengaruhi probabilitas terjadinya kejadian lainnya. Dalam kasus ini, rumus peluang yang digunakan sedikit berbeda dibandingkan dengan kejadian saling bebas. Rumus ini membantu kita menghitung probabilitas terjadinya kedua kejadian secara bersamaan, dengan mempertimbangkan pengaruh satu kejadian terhadap yang lain.
Rumus Peluang Kejadian Tidak Saling Bebas
Rumus untuk menghitung peluang kejadian tidak saling bebas adalah:
P(A dan B) = P(A) * P(B|A)
Dimana:
- P(A dan B) adalah peluang kejadian A dan B terjadi bersamaan.
- P(A) adalah peluang kejadian A terjadi.
- P(B|A) adalah peluang kejadian B terjadi, dengan syarat kejadian A sudah terjadi. Ini disebut peluang bersyarat.
Contoh Penerapan Rumus
Misalnya, kita memiliki kotak berisi 5 bola merah dan 3 bola biru. Kita mengambil satu bola secara acak, kemudian mengambil bola kedua tanpa mengembalikan bola pertama. Kita ingin menghitung peluang mengambil bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua.
Misalkan:
- A: Kejadian mengambil bola merah pada pengambilan pertama.
- B: Kejadian mengambil bola biru pada pengambilan kedua.
Maka:
- P(A) = 5/8 (peluang mengambil bola merah pada pengambilan pertama)
- P(B|A) = 3/7 (peluang mengambil bola biru pada pengambilan kedua, dengan syarat bola merah sudah diambil pada pengambilan pertama)
Jadi, peluang mengambil bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua adalah:
P(A dan B) = P(A) * P(B|A) = (5/8) * (3/7) = 15/56
Artinya, peluang mengambil bola merah dan kemudian bola biru adalah 15/56.
Contoh Soal dan Penyelesaian
Setelah memahami konsep dasar peluang kejadian tidak saling bebas, mari kita bahas beberapa contoh soal dan penyelesaiannya. Contoh soal ini akan membantu Anda untuk lebih memahami cara menerapkan rumus peluang kejadian tidak saling bebas dalam menyelesaikan masalah.
Contoh Soal 1: Mengambil Bola dari Kantong, Contoh soal peluang kejadian tidak saling bebas
Misalkan dalam sebuah kantong terdapat 5 bola merah dan 3 bola biru. Anda mengambil satu bola secara acak, dan tanpa mengembalikannya, Anda mengambil satu bola lagi. Hitunglah peluang Anda mengambil bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua.
Langkah-langkah Penyelesaian
- Tentukan kejadian-kejadian yang terlibat.
- Hitung peluang kejadian pertama.
- Hitung peluang kejadian kedua, dengan mempertimbangkan bahwa kejadian pertama telah terjadi.
- Hitung peluang kejadian gabungan.
Kejadian pertama adalah mengambil bola merah pada pengambilan pertama (M1). Kejadian kedua adalah mengambil bola biru pada pengambilan kedua (B2).
Peluang mengambil bola merah pada pengambilan pertama adalah 5/8 karena terdapat 5 bola merah dari total 8 bola.
Karena bola pertama tidak dikembalikan, maka pada pengambilan kedua hanya tersisa 7 bola. Karena bola merah pertama sudah diambil, maka hanya tersisa 3 bola biru. Jadi, peluang mengambil bola biru pada pengambilan kedua adalah 3/7.
Peluang mengambil bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua adalah hasil kali peluang kedua kejadian tersebut, yaitu:
P(M1 dan B2) = P(M1) * P(B2 | M1) = (5/8) * (3/7) = 15/56.
Contoh Soal 2: Mengambil Kartu dari Dek
Anda mengambil satu kartu secara acak dari dek kartu standar 52 kartu. Kemudian, tanpa mengembalikan kartu pertama, Anda mengambil satu kartu lagi. Hitunglah peluang Anda mengambil kartu As pada pengambilan pertama dan kartu King pada pengambilan kedua.
Langkah-langkah Penyelesaian
- Tentukan kejadian-kejadian yang terlibat.
- Hitung peluang kejadian pertama.
- Hitung peluang kejadian kedua, dengan mempertimbangkan bahwa kejadian pertama telah terjadi.
- Hitung peluang kejadian gabungan.
Kejadian pertama adalah mengambil kartu As pada pengambilan pertama (A1). Kejadian kedua adalah mengambil kartu King pada pengambilan kedua (K2).
Peluang mengambil kartu As pada pengambilan pertama adalah 4/52 karena terdapat 4 kartu As dari total 52 kartu.
Karena kartu pertama tidak dikembalikan, maka pada pengambilan kedua hanya tersisa 51 kartu. Karena kartu As pertama sudah diambil, maka masih terdapat 4 kartu King. Jadi, peluang mengambil kartu King pada pengambilan kedua adalah 4/51.
Peluang mengambil kartu As pada pengambilan pertama dan kartu King pada pengambilan kedua adalah hasil kali peluang kedua kejadian tersebut, yaitu:
P(A1 dan K2) = P(A1) * P(K2 | A1) = (4/52) * (4/51) = 4/663.
Aplikasi Kejadian Tidak Saling Bebas dalam Kehidupan Nyata
Kejadian tidak saling bebas adalah konsep penting dalam probabilitas yang menggambarkan situasi di mana kejadian satu memengaruhi kemungkinan kejadian lainnya. Dalam kehidupan nyata, banyak kejadian yang saling terkait, dan memahami konsep ini dapat membantu kita menganalisis dan memprediksi hasil dari berbagai situasi.
Aplikasi dalam Bidang Kesehatan
Dalam bidang kesehatan, banyak contoh kejadian tidak saling bebas yang memengaruhi hasil pengobatan dan kesehatan individu.
- Penggunaan antibiotik dan resistensi bakteri: Penggunaan antibiotik yang berlebihan dapat menyebabkan resistensi bakteri, sehingga antibiotik tersebut menjadi kurang efektif untuk pengobatan infeksi di masa depan. Kejadian penggunaan antibiotik dan resistensi bakteri saling terkait, karena penggunaan antibiotik memengaruhi kemungkinan bakteri menjadi resisten.
- Vaksinasi dan kekebalan: Vaksinasi membantu meningkatkan kekebalan tubuh terhadap penyakit tertentu. Kejadian vaksinasi dan kekebalan saling terkait, karena vaksinasi meningkatkan kemungkinan seseorang menjadi kebal terhadap penyakit tersebut.
- Merokok dan penyakit paru-paru: Merokok adalah faktor risiko utama untuk penyakit paru-paru, seperti kanker paru-paru dan penyakit paru obstruktif kronis (PPOK). Kejadian merokok dan penyakit paru-paru saling terkait, karena merokok meningkatkan kemungkinan seseorang terkena penyakit paru-paru.
Aplikasi dalam Bidang Ekonomi
Konsep kejadian tidak saling bebas juga relevan dalam bidang ekonomi, di mana berbagai faktor saling memengaruhi satu sama lain.
- Harga minyak dan inflasi: Kenaikan harga minyak dapat menyebabkan inflasi, karena biaya produksi barang dan jasa meningkat. Kejadian harga minyak dan inflasi saling terkait, karena perubahan harga minyak memengaruhi tingkat inflasi.
- Suku bunga dan investasi: Kenaikan suku bunga dapat mengurangi investasi, karena biaya pinjaman menjadi lebih mahal. Kejadian suku bunga dan investasi saling terkait, karena suku bunga memengaruhi tingkat investasi.
- Nilai tukar dan perdagangan internasional: Penurunan nilai tukar suatu mata uang dapat meningkatkan ekspor dan mengurangi impor. Kejadian nilai tukar dan perdagangan internasional saling terkait, karena nilai tukar memengaruhi daya saing ekspor dan impor suatu negara.
Aplikasi dalam Bidang Sosial
Dalam bidang sosial, banyak contoh kejadian tidak saling bebas yang memengaruhi kehidupan manusia.
- Pendidikan dan pendapatan: Tingkat pendidikan seseorang dapat memengaruhi pendapatannya. Kejadian pendidikan dan pendapatan saling terkait, karena pendidikan dapat meningkatkan peluang mendapatkan pekerjaan dengan gaji yang lebih tinggi.
- Kemiskinan dan kesehatan: Kemiskinan dapat menyebabkan akses terbatas terhadap layanan kesehatan, yang dapat memengaruhi kesehatan seseorang. Kejadian kemiskinan dan kesehatan saling terkait, karena kemiskinan dapat meningkatkan risiko penyakit dan kematian.
- Diskriminasi dan peluang: Diskriminasi dapat membatasi peluang seseorang dalam kehidupan, seperti akses terhadap pekerjaan, pendidikan, dan perumahan. Kejadian diskriminasi dan peluang saling terkait, karena diskriminasi dapat mengurangi kesempatan seseorang untuk sukses.
Perbedaan Kejadian Tidak Saling Bebas dengan Kejadian Saling Bebas
Dalam teori peluang, memahami perbedaan antara kejadian saling bebas dan kejadian tidak saling bebas sangat penting. Ini karena cara menghitung peluang kejadian tersebut berbeda, dan perbedaan ini bisa berdampak besar pada hasil akhir.
Perbedaan Dasar
Kejadian saling bebas adalah kejadian di mana hasil dari satu kejadian tidak memengaruhi hasil dari kejadian lainnya. Contohnya, jika kita melempar koin dua kali, hasil lemparan pertama tidak memengaruhi hasil lemparan kedua. Sementara itu, kejadian tidak saling bebas adalah kejadian di mana hasil dari satu kejadian memengaruhi hasil dari kejadian lainnya.
Contoh Soal Kejadian Saling Bebas
Misalnya, kita memiliki sebuah kotak berisi 5 bola merah dan 5 bola biru. Kita mengambil satu bola secara acak, kemudian mengembalikannya ke kotak sebelum mengambil bola kedua. Kejadian mengambil bola merah pada pengambilan pertama dan kejadian mengambil bola biru pada pengambilan kedua adalah kejadian saling bebas. Ini karena mengembalikan bola pertama ke kotak memastikan bahwa peluang mengambil bola merah atau biru pada pengambilan kedua tetap sama, yaitu 5/10.
Contoh Soal Kejadian Tidak Saling Bebas
Misalnya, kita memiliki sebuah kotak berisi 5 bola merah dan 5 bola biru. Kita mengambil satu bola secara acak, tetapi tidak mengembalikannya ke kotak sebelum mengambil bola kedua. Kejadian mengambil bola merah pada pengambilan pertama dan kejadian mengambil bola biru pada pengambilan kedua adalah kejadian tidak saling bebas. Ini karena tidak mengembalikan bola pertama ke kotak akan mengurangi jumlah bola di kotak, sehingga memengaruhi peluang mengambil bola biru pada pengambilan kedua.
Cara Menghitung Peluang
Untuk menghitung peluang kejadian saling bebas, kita cukup mengalikan peluang setiap kejadian. Misalnya, jika peluang mengambil bola merah pada pengambilan pertama adalah 5/10 dan peluang mengambil bola biru pada pengambilan kedua adalah 5/10, maka peluang mengambil bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua adalah (5/10) * (5/10) = 25/100.
Untuk menghitung peluang kejadian tidak saling bebas, kita perlu menggunakan konsep peluang bersyarat. Peluang bersyarat adalah peluang suatu kejadian terjadi, dengan syarat bahwa kejadian lain telah terjadi. Misalnya, peluang mengambil bola biru pada pengambilan kedua, dengan syarat bahwa bola merah telah diambil pada pengambilan pertama, adalah 5/9 (karena hanya ada 9 bola tersisa di kotak, dan 5 di antaranya adalah biru). Peluang mengambil bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua adalah (5/10) * (5/9) = 25/90.
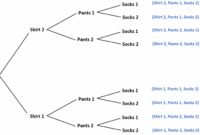
Diagram Pohon untuk Kejadian Tidak Saling Bebas: Contoh Soal Peluang Kejadian Tidak Saling Bebas
Diagram pohon adalah alat visual yang sangat berguna untuk memahami dan menghitung peluang kejadian, terutama dalam kasus kejadian tidak saling bebas. Dalam kejadian tidak saling bebas, hasil dari satu kejadian dapat memengaruhi hasil kejadian lainnya. Diagram pohon membantu kita melacak semua kemungkinan hasil dan menghitung peluang setiap kombinasi hasil.
Cara Menggambar Diagram Pohon
Berikut adalah langkah-langkah umum untuk menggambar diagram pohon untuk kejadian tidak saling bebas:
- Tentukan kejadian-kejadian yang ingin Anda analisis. Misalnya, Anda mungkin ingin menganalisis peluang seseorang mendapatkan nilai A dalam ujian matematika dan fisika.
- Mulailah dengan cabang pertama dari pohon Anda. Cabang ini mewakili kejadian pertama. Label setiap cabang dengan kemungkinan kejadian tersebut. Misalnya, jika peluang seseorang mendapatkan nilai A dalam ujian matematika adalah 0,7, label cabang tersebut dengan “A (0,7)”.
- Dari setiap cabang pada tingkat pertama, tambahkan cabang-cabang baru untuk mewakili kejadian kedua. Label cabang-cabang ini dengan kemungkinan kejadian kedua, mengingat kejadian pertama telah terjadi. Misalnya, jika peluang seseorang mendapatkan nilai A dalam ujian fisika setelah mendapatkan nilai A dalam ujian matematika adalah 0,6, label cabang tersebut dengan “A (0,6)”.
- Lanjutkan proses ini untuk semua kejadian berikutnya. Perhatikan bahwa kemungkinan kejadian berikutnya dapat berubah tergantung pada hasil kejadian sebelumnya.
Contoh Soal
Sebuah kotak berisi 5 bola merah dan 3 bola biru. Dua bola diambil secara bergantian tanpa pengembalian. Hitung peluang bahwa kedua bola yang diambil berwarna merah.
Diagram pohon untuk soal ini dapat digambar sebagai berikut:
Dari diagram pohon, kita dapat melihat bahwa peluang mengambil dua bola merah secara bergantian tanpa pengembalian adalah:
P(Merah, Merah) = P(Merah) * P(Merah | Merah) = (5/8) * (4/7) = 5/14
Diagram pohon membantu kita memvisualisasikan semua kemungkinan hasil dan menghitung peluang setiap kombinasi hasil. Ini sangat berguna untuk memecahkan masalah peluang yang melibatkan kejadian tidak saling bebas, di mana hasil dari satu kejadian dapat memengaruhi hasil kejadian lainnya.
Penggunaan Tabel Kontingensi untuk Kejadian Tidak Saling Bebas

Kejadian tidak saling bebas adalah kejadian di mana peluang terjadinya satu kejadian memengaruhi peluang terjadinya kejadian lainnya. Dalam kasus seperti ini, tabel kontingensi dapat menjadi alat yang sangat berguna untuk menganalisis dan menghitung peluang kejadian.
Membuat Tabel Kontingensi untuk Kejadian Tidak Saling Bebas
Tabel kontingensi adalah tabel yang menunjukkan frekuensi bersama dari dua atau lebih variabel kategorikal. Dalam konteks kejadian tidak saling bebas, tabel ini menampilkan frekuensi bersama dari kejadian yang terkait. Berikut adalah cara membuat tabel kontingensi untuk kejadian tidak saling bebas:
- Tentukan variabel kategorikal yang akan dianalisis. Variabel ini harus mewakili kejadian yang tidak saling bebas.
- Buat tabel dengan baris yang mewakili satu variabel dan kolom yang mewakili variabel lainnya.
- Isi setiap sel dalam tabel dengan frekuensi bersama dari kedua variabel.
Cara Tabel Kontingensi Membantu Menghitung Peluang Kejadian
Tabel kontingensi memudahkan dalam menghitung peluang kejadian dengan cara berikut:
- Menghitung peluang bersyarat: Tabel kontingensi membantu kita menghitung peluang suatu kejadian terjadi, dengan syarat kejadian lain telah terjadi. Misalnya, kita dapat menghitung peluang seseorang menyukai film horor, dengan syarat orang tersebut juga menyukai film thriller.
- Menghitung peluang bersama: Tabel kontingensi juga memungkinkan kita untuk menghitung peluang bersama dari dua kejadian. Ini adalah peluang kedua kejadian tersebut terjadi secara bersamaan.
- Menganalisis hubungan antara kejadian: Tabel kontingensi dapat membantu kita menganalisis hubungan antara dua kejadian. Misalnya, kita dapat melihat apakah ada hubungan antara jenis kelamin dan preferensi film.
Contoh Soal dan Solusi
Misalnya, sebuah perusahaan melakukan survei terhadap 100 karyawannya untuk mengetahui preferensi mereka terhadap dua jenis minuman, kopi dan teh. Hasil survei ditunjukkan dalam tabel kontingensi berikut:
| Kopi | Teh | Total | |
|---|---|---|---|
| Pria | 30 | 10 | 40 |
| Wanita | 20 | 40 | 60 |
| Total | 50 | 50 | 100 |
Dari tabel tersebut, kita dapat menghitung berbagai peluang, seperti:
- Peluang seorang karyawan menyukai kopi: 50/100 = 0,5
- Peluang seorang karyawan menyukai teh: 50/100 = 0,5
- Peluang seorang karyawan adalah pria dan menyukai kopi: 30/100 = 0,3
- Peluang seorang karyawan menyukai kopi, dengan syarat karyawan tersebut adalah pria: 30/40 = 0,75
- Peluang seorang karyawan menyukai teh, dengan syarat karyawan tersebut adalah wanita: 40/60 = 0,67
Contoh ini menunjukkan bagaimana tabel kontingensi dapat digunakan untuk menganalisis dan menghitung peluang kejadian tidak saling bebas. Dengan menggunakan tabel ini, kita dapat memperoleh informasi berharga tentang hubungan antara kejadian dan peluang kejadian terjadi.
Hubungan Kejadian Tidak Saling Bebas dengan Kejadian Bersyarat
Dalam dunia probabilitas, kita sering kali menjumpai kejadian yang saling memengaruhi. Kejadian-kejadian ini disebut sebagai kejadian tidak saling bebas. Kejadian tidak saling bebas memiliki hubungan erat dengan konsep kejadian bersyarat, di mana peluang suatu kejadian dipengaruhi oleh terjadinya kejadian lain sebelumnya.
Hubungan Kejadian Tidak Saling Bebas dan Kejadian Bersyarat
Kejadian tidak saling bebas terjadi ketika peluang suatu kejadian dipengaruhi oleh terjadinya kejadian lain sebelumnya. Dengan kata lain, informasi tentang terjadinya suatu kejadian dapat mengubah peluang kejadian lainnya. Kejadian bersyarat, di sisi lain, mengukur peluang suatu kejadian terjadi dengan asumsi bahwa kejadian lain telah terjadi sebelumnya. Hubungan antara kedua konsep ini terletak pada bagaimana kejadian bersyarat dapat digunakan untuk menghitung peluang kejadian tidak saling bebas.
Contoh Soal Hubungan Kejadian Tidak Saling Bebas dan Kejadian Bersyarat
Misalkan kita memiliki kotak berisi 5 bola merah dan 3 bola biru. Kita akan mengambil 2 bola secara acak tanpa pengembalian. Peristiwa pertama adalah mengambil bola merah, dan peristiwa kedua adalah mengambil bola biru. Kejadian ini tidak saling bebas karena pengambilan bola pertama akan memengaruhi peluang pengambilan bola kedua. Misalnya, jika kita mengambil bola merah pada pengambilan pertama, maka peluang mengambil bola biru pada pengambilan kedua akan lebih rendah karena jumlah bola merah di kotak berkurang.
Untuk menghitung peluang mengambil bola biru pada pengambilan kedua dengan syarat bola merah diambil pada pengambilan pertama, kita menggunakan konsep kejadian bersyarat. Peluang mengambil bola biru pada pengambilan kedua dengan syarat bola merah diambil pada pengambilan pertama dilambangkan dengan P(Biru | Merah). Dalam contoh ini, kita dapat menghitung P(Biru | Merah) sebagai berikut:
P(Biru | Merah) = (Jumlah bola biru) / (Jumlah total bola setelah bola merah diambil) = 3 / 7
Dengan demikian, peluang mengambil bola biru pada pengambilan kedua dengan syarat bola merah diambil pada pengambilan pertama adalah 3/7.
Menerapkan Konsep Kejadian Bersyarat dalam Menghitung Peluang Kejadian Tidak Saling Bebas
Konsep kejadian bersyarat dapat digunakan untuk menghitung peluang kejadian tidak saling bebas dengan menggunakan rumus berikut:
P(A dan B) = P(A) * P(B | A)
di mana:
- P(A dan B) adalah peluang kejadian A dan B terjadi bersamaan.
- P(A) adalah peluang kejadian A terjadi.
- P(B | A) adalah peluang kejadian B terjadi dengan syarat kejadian A telah terjadi.
Rumus ini menunjukkan bahwa peluang kejadian A dan B terjadi bersamaan sama dengan peluang kejadian A terjadi dikalikan dengan peluang kejadian B terjadi dengan syarat kejadian A telah terjadi.
Dengan menggunakan rumus ini, kita dapat menghitung peluang kejadian tidak saling bebas dengan menggunakan informasi tentang peluang kejadian bersyarat. Contohnya, dalam contoh soal di atas, kita dapat menghitung peluang mengambil bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua sebagai berikut:
P(Merah dan Biru) = P(Merah) * P(Biru | Merah) = (5/8) * (3/7) = 15/56
Dengan demikian, peluang mengambil bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua adalah 15/56.
Penerapan Konsep Kejadian Tidak Saling Bebas dalam Statistik
Dalam dunia statistik, memahami konsep kejadian saling bebas dan tidak saling bebas merupakan hal yang penting. Kejadian tidak saling bebas terjadi ketika hasil dari satu kejadian memengaruhi hasil dari kejadian lainnya. Konsep ini memiliki peran penting dalam berbagai bidang, termasuk pengambilan sampel, analisis data, dan inferensi statistik.
Contoh Aplikasi Kejadian Tidak Saling Bebas dalam Pengambilan Sampel
Misalkan kita ingin meneliti preferensi minuman di sebuah kelas. Kita mengambil sampel 10 siswa dan menanyakan minuman favorit mereka. Ternyata, 5 siswa memilih teh, 3 siswa memilih kopi, dan 2 siswa memilih jus. Jika kita ingin mengambil sampel kedua, dan kita ingin mengetahui apakah ada hubungan antara preferensi minuman dengan jenis kelamin, maka kejadian ini tidak saling bebas. Karena, jika dalam sampel pertama, banyak siswa yang memilih teh, maka dalam sampel kedua, kemungkinan besar akan lebih banyak siswa yang memilih teh, terutama jika sebagian besar siswa di kelas tersebut adalah perempuan.
Penggunaan Konsep Kejadian Tidak Saling Bebas dalam Analisis Data
Konsep kejadian tidak saling bebas digunakan dalam analisis data untuk mengidentifikasi hubungan antar variabel. Misalnya, dalam studi medis, peneliti mungkin ingin mengetahui apakah ada hubungan antara merokok dan penyakit jantung. Jika mereka menemukan bahwa orang yang merokok lebih mungkin terkena penyakit jantung, maka mereka dapat menyimpulkan bahwa merokok dan penyakit jantung adalah kejadian yang tidak saling bebas.
Pengaruh Kejadian Tidak Saling Bebas terhadap Hasil Inferensi Statistik
Kejadian tidak saling bebas dapat memengaruhi hasil inferensi statistik. Misalnya, jika kita ingin menguji hipotesis tentang efektivitas suatu obat, dan kita tidak memperhitungkan kejadian tidak saling bebas, maka kita mungkin mendapatkan hasil yang bias.
- Misalnya, jika kita ingin menguji efektivitas obat baru untuk mengobati tekanan darah tinggi, dan kita tidak memperhitungkan kejadian tidak saling bebas, maka kita mungkin mendapatkan hasil yang bias. Hal ini karena orang yang diberi obat baru mungkin memiliki faktor risiko lain yang juga dapat memengaruhi tekanan darah mereka, seperti gaya hidup atau riwayat keluarga.
Pertimbangan dan Kesulitan dalam Menganalisis Kejadian Tidak Saling Bebas
Analisis kejadian tidak saling bebas merupakan bagian penting dalam memahami hubungan antar peristiwa. Namun, proses ini memiliki tantangan tersendiri yang perlu dipertimbangkan. Artikel ini akan membahas beberapa pertimbangan dan kesulitan yang sering dihadapi dalam menganalisis kejadian tidak saling bebas.
Contoh soal peluang kejadian tidak saling bebas seringkali melibatkan dua kejadian yang saling memengaruhi. Misalnya, dalam sebuah kotak terdapat 5 bola merah dan 3 bola biru. Jika kita mengambil satu bola, lalu tanpa mengembalikannya, kita mengambil bola kedua, maka peluang mendapatkan bola merah pada pengambilan kedua akan dipengaruhi oleh warna bola yang diambil pertama kali.
Konsep ini mirip dengan contoh soal bep unit contoh soal bep unit yang membahas tentang titik impas produksi, di mana setiap unit yang diproduksi akan memengaruhi total biaya produksi. Kembali ke soal peluang, untuk menghitung peluang kejadian tidak saling bebas, kita perlu mempertimbangkan pengaruh kejadian pertama terhadap kejadian kedua.
Identifikasi Kesulitan dalam Menentukan Apakah Kejadian Saling Bebas atau Tidak
Menentukan apakah dua kejadian saling bebas atau tidak merupakan langkah awal yang krusial dalam analisis. Sayangnya, proses ini tidak selalu mudah. Berikut beberapa kesulitan yang mungkin dihadapi:
- Kurangnya Data yang Cukup: Membuat kesimpulan tentang ketergantungan antar kejadian memerlukan data yang cukup dan representatif. Jika data terbatas, sulit untuk memastikan apakah ketergantungan tersebut benar-benar ada atau hanya sebuah kebetulan.
- Kompleksitas Hubungan: Hubungan antar kejadian bisa sangat kompleks dan tidak selalu linear. Kadang-kadang, ketergantungan antar kejadian tersembunyi di balik faktor-faktor lain yang tidak terlihat secara langsung.
- Pengaruh Faktor Lain: Kejadian yang tampak saling bebas mungkin saja dipengaruhi oleh faktor-faktor lain yang tidak teramati. Hal ini dapat menyebabkan kesimpulan yang salah tentang ketergantungan antar kejadian.
Pentingnya Data yang Akurat dan Relevan dalam Analisis Kejadian Tidak Saling Bebas
Data yang akurat dan relevan merupakan fondasi dari analisis kejadian tidak saling bebas yang valid. Data yang berkualitas rendah dapat menyebabkan hasil analisis yang bias dan tidak dapat diandalkan. Berikut beberapa poin penting terkait data:
- Akurasi Data: Data yang digunakan dalam analisis harus akurat dan bebas dari kesalahan. Kesalahan dalam pengumpulan atau pencatatan data dapat menyebabkan bias dalam hasil analisis.
- Relevansi Data: Data yang digunakan harus relevan dengan pertanyaan penelitian yang ingin dijawab. Data yang tidak relevan dapat menyesatkan hasil analisis dan membuat kesimpulan yang tidak valid.
- Representasi Data: Data yang digunakan harus representatif dari populasi yang ingin dipelajari. Jika data tidak representatif, hasil analisis mungkin tidak dapat digeneralisasikan ke populasi yang lebih luas.
Pengaruh Bias Data terhadap Hasil Analisis
Bias data dapat terjadi dalam berbagai bentuk dan dapat mempengaruhi hasil analisis secara signifikan. Berikut beberapa jenis bias data yang perlu diwaspadai:
- Bias Pemilihan: Terjadi ketika sampel yang digunakan dalam analisis tidak representatif dari populasi yang ingin dipelajari. Contohnya, jika penelitian hanya melibatkan responden dari kelompok tertentu, hasil analisis mungkin tidak dapat digeneralisasikan ke populasi yang lebih luas.
- Bias Pengukuran: Terjadi ketika alat ukur yang digunakan untuk mengumpulkan data tidak akurat atau tidak reliabel. Contohnya, jika kuesioner yang digunakan dalam penelitian mengandung pertanyaan yang bias, hasil analisis mungkin tidak mencerminkan kenyataan.
- Bias Konfirmasi: Terjadi ketika peneliti cenderung mencari data yang mendukung hipotesis mereka dan mengabaikan data yang bertentangan. Hal ini dapat menyebabkan interpretasi hasil analisis yang bias.
Contoh Soal Peluang Kejadian Tidak Saling Bebas dalam Berbagai Konteks
Peluang kejadian tidak saling bebas terjadi ketika hasil dari satu kejadian memengaruhi hasil kejadian lainnya. Dalam konteks ini, kita akan menjelajahi beberapa contoh soal yang melibatkan kejadian tidak saling bebas dalam berbagai bidang, mulai dari kesehatan hingga ekonomi dan sosial.
Contoh Soal dalam Konteks Kesehatan
Contoh soal peluang kejadian tidak saling bebas dalam konteks kesehatan dapat diilustrasikan dengan kasus pasien yang mengalami penyakit kronis, seperti diabetes. Kondisi ini dapat memengaruhi peluang pasien mengalami komplikasi kesehatan lainnya, seperti penyakit jantung atau stroke. Misalnya, seorang pasien diabetes memiliki peluang lebih tinggi mengalami serangan jantung dibandingkan dengan orang yang tidak menderita diabetes.
- Misalnya, sebuah penelitian menunjukkan bahwa 30% pasien diabetes mengalami serangan jantung dalam jangka waktu 10 tahun. Jika diketahui bahwa 10% populasi menderita diabetes, berapakah peluang seseorang mengalami serangan jantung dalam 10 tahun mendatang, dengan asumsi bahwa seseorang dipilih secara acak dari populasi?
Contoh Soal dalam Konteks Ekonomi
Dalam konteks ekonomi, contoh soal peluang kejadian tidak saling bebas dapat ditemukan pada analisis pasar saham. Harga saham perusahaan tertentu dapat dipengaruhi oleh berbagai faktor, termasuk kondisi ekonomi global, kinerja perusahaan, dan sentimen investor. Misalnya, penurunan harga minyak bumi dapat memengaruhi harga saham perusahaan minyak, karena hal ini dapat berdampak pada keuntungan perusahaan.
- Misalnya, jika peluang saham perusahaan A naik 20% jika ekonomi global membaik, dan peluang ekonomi global membaik adalah 50%, berapakah peluang saham perusahaan A naik?
Contoh Soal dalam Konteks Sosial
Contoh soal peluang kejadian tidak saling bebas dalam konteks sosial dapat diilustrasikan dengan kasus pernikahan. Misalnya, seseorang yang menikah dengan pasangan yang memiliki latar belakang pendidikan tinggi memiliki peluang lebih tinggi untuk mendapatkan pekerjaan yang lebih baik dan memiliki pendapatan yang lebih tinggi. Hal ini karena pendidikan pasangan dapat memengaruhi jaringan sosial dan peluang karier individu.
- Misalnya, jika peluang seseorang mendapatkan pekerjaan dengan gaji tinggi adalah 60% jika pasangannya memiliki gelar sarjana, dan peluang pasangannya memiliki gelar sarjana adalah 70%, berapakah peluang seseorang mendapatkan pekerjaan dengan gaji tinggi?
Ringkasan Penutup
Memahami konsep kejadian tidak saling bebas sangat penting dalam berbagai bidang, seperti kesehatan, ekonomi, dan sosial. Dengan memahami bagaimana kejadian saling terkait, kita dapat membuat prediksi yang lebih akurat, mengambil keputusan yang lebih baik, dan bahkan mengembangkan strategi yang lebih efektif untuk berbagai situasi. Jadi, jangan ragu untuk menjelajahi contoh soal dan aplikasi yang telah dibahas dalam artikel ini untuk memperdalam pemahaman Anda tentang konsep penting ini.