Contoh soal peluang kejadian tidak saling lepas dan pembahasannya – Pernahkah kamu bertanya-tanya bagaimana peluang seseorang bisa mendapatkan kartu As dan kartu berwarna merah dalam satu kali pengambilan kartu dari setumpuk kartu remi? Atau, bagaimana peluang seseorang bisa mendapatkan nilai A dalam ujian matematika dan fisika? Ini adalah contoh dari kejadian yang tidak saling lepas, di mana dua kejadian bisa terjadi secara bersamaan.
Dalam artikel ini, kita akan membahas tentang peluang kejadian tidak saling lepas. Mulai dari definisi, rumus, contoh soal, hingga aplikasi dalam kehidupan sehari-hari. Simak penjelasannya agar kamu dapat memahami konsep ini dengan lebih baik!
Pengertian Kejadian Tidak Saling Lepas
Dalam teori peluang, kejadian tidak saling lepas merupakan konsep yang penting untuk memahami bagaimana peluang suatu kejadian dapat dipengaruhi oleh kejadian lain. Kejadian tidak saling lepas terjadi ketika hasil dari satu kejadian dapat memengaruhi hasil dari kejadian lainnya.
Pengertian Kejadian Tidak Saling Lepas
Kejadian tidak saling lepas, dalam teori peluang, adalah dua atau lebih kejadian yang memiliki kemungkinan untuk terjadi bersamaan. Artinya, hasil dari satu kejadian dapat memengaruhi hasil dari kejadian lainnya.
Contoh Kejadian Tidak Saling Lepas dalam Kehidupan Sehari-hari
- Misalnya, ketika kita mengambil kartu dari satu set kartu remi, peluang kita untuk mendapatkan kartu As setelah mengambil kartu Jack akan berbeda dengan peluang kita untuk mendapatkan kartu As jika kita tidak mengambil kartu Jack terlebih dahulu. Ini karena kejadian mengambil kartu Jack memengaruhi jumlah kartu yang tersisa dalam set kartu, sehingga memengaruhi peluang kita untuk mendapatkan kartu As.
- Contoh lainnya, jika kita melempar dua koin secara bersamaan, kejadian mendapatkan sisi gambar pada koin pertama akan memengaruhi peluang mendapatkan sisi gambar pada koin kedua. Jika koin pertama menghasilkan sisi gambar, maka peluang mendapatkan sisi gambar pada koin kedua akan lebih rendah karena hanya tersisa satu koin yang belum dilempar.
Contoh Kejadian Tidak Saling Lepas dalam Konteks Matematika
- Misalkan kita memiliki sebuah kotak berisi 5 bola merah dan 3 bola biru. Kita mengambil satu bola dari kotak secara acak. Peluang kita untuk mendapatkan bola merah adalah 5/8. Jika kita mengambil bola pertama dan ternyata merah, maka peluang kita untuk mendapatkan bola merah lagi pada pengambilan kedua akan menjadi 4/7 karena hanya tersisa 4 bola merah dan 7 bola total. Kejadian ini tidak saling lepas karena pengambilan bola pertama memengaruhi peluang pengambilan bola kedua.
Rumus Peluang Kejadian Tidak Saling Lepas: Contoh Soal Peluang Kejadian Tidak Saling Lepas Dan Pembahasannya
Pada materi sebelumnya, kita telah membahas tentang peluang kejadian saling lepas. Nah, sekarang kita akan mempelajari tentang peluang kejadian yang tidak saling lepas. Kejadian tidak saling lepas adalah kejadian yang memiliki anggota (unsur) yang sama. Artinya, kedua kejadian tersebut bisa terjadi bersamaan. Sebagai contoh, saat kita mengambil kartu dari satu set kartu remi, mengambil kartu As dan kartu bergambar merupakan kejadian yang tidak saling lepas karena kartu As bergambar juga termasuk dalam kedua kejadian tersebut.
Untuk menghitung peluang kejadian tidak saling lepas, kita menggunakan rumus yang sedikit berbeda dari rumus peluang kejadian saling lepas. Rumus ini mempertimbangkan kemungkinan kedua kejadian terjadi bersamaan.
Rumus Peluang Kejadian Tidak Saling Lepas
Rumus peluang kejadian tidak saling lepas adalah sebagai berikut:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
Dimana:
- P(A ∪ B) adalah peluang kejadian A atau B terjadi.
- P(A) adalah peluang kejadian A terjadi.
- P(B) adalah peluang kejadian B terjadi.
- P(A ∩ B) adalah peluang kejadian A dan B terjadi bersamaan.
Contoh Perhitungan Peluang Kejadian Tidak Saling Lepas
Misalnya, kita memiliki sebuah kotak berisi 5 bola merah, 3 bola biru, dan 2 bola hijau. Kita mengambil satu bola secara acak dari kotak tersebut. Hitunglah peluang terambilnya bola merah atau bola biru.
Kita dapat menggunakan rumus peluang kejadian tidak saling lepas untuk menyelesaikan masalah ini. Misalkan:
- A adalah kejadian terambilnya bola merah.
- B adalah kejadian terambilnya bola biru.
Maka, kita dapat menghitung peluangnya sebagai berikut:
- P(A) = 5/10 = 1/2 (peluang terambilnya bola merah)
- P(B) = 3/10 (peluang terambilnya bola biru)
- P(A ∩ B) = 0 (peluang terambilnya bola merah dan biru bersamaan adalah 0 karena tidak ada bola yang berwarna merah dan biru)
Dengan menggunakan rumus peluang kejadian tidak saling lepas, kita dapat menghitung peluang terambilnya bola merah atau bola biru:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 1/2 + 3/10 – 0 = 4/5
Jadi, peluang terambilnya bola merah atau bola biru adalah 4/5.
Contoh Soal Peluang Kejadian Tidak Saling Lepas
Dalam dunia probabilitas, memahami konsep peluang kejadian tidak saling lepas sangat penting. Kejadian tidak saling lepas terjadi ketika hasil dari satu kejadian dapat memengaruhi hasil kejadian lainnya. Untuk mengilustrasikan konsep ini, mari kita bahas beberapa contoh soal dengan tingkat kesulitan yang bervariasi.
Contoh Soal Peluang Kejadian Tidak Saling Lepas (Tingkat Kesulitan Mudah)
Misalnya, dalam sebuah kotak terdapat 5 bola merah dan 3 bola biru. Anda mengambil satu bola secara acak, kemudian tanpa mengembalikan bola pertama, Anda mengambil satu bola lagi. Tentukan peluang Anda mendapatkan bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua.
Contoh soal peluang kejadian tidak saling lepas dan pembahasannya memang menarik, karena kita harus memahami konsep ketergantungan antara kejadian. Hal ini mirip dengan konsep dalam contoh soal matematika keuangan , di mana kita harus memahami ketergantungan antara berbagai faktor seperti suku bunga, inflasi, dan nilai investasi.
Contoh soal peluang kejadian tidak saling lepas sering kali melibatkan perhitungan peluang bersyarat, yang serupa dengan perhitungan return on investment (ROI) dalam matematika keuangan.
- Peluang mendapatkan bola merah pada pengambilan pertama adalah 5/8 (karena ada 5 bola merah dari total 8 bola).
- Setelah mengambil bola merah, tersisa 7 bola di kotak, dengan 3 bola biru di antaranya. Peluang mendapatkan bola biru pada pengambilan kedua adalah 3/7.
- Oleh karena itu, peluang mendapatkan bola merah pada pengambilan pertama dan bola biru pada pengambilan kedua adalah (5/8) * (3/7) = 15/56.
Contoh Soal Peluang Kejadian Tidak Saling Lepas (Tingkat Kesulitan Sedang)
Sebuah toko menjual dua jenis kue, yaitu kue cokelat dan kue keju. Diketahui bahwa 60% pelanggan membeli kue cokelat, 50% pelanggan membeli kue keju, dan 30% pelanggan membeli kedua jenis kue tersebut. Tentukan peluang seorang pelanggan yang membeli kue cokelat juga membeli kue keju.
- Misalkan A adalah kejadian membeli kue cokelat dan B adalah kejadian membeli kue keju.
- Kita tahu P(A) = 0.6, P(B) = 0.5, dan P(A∩B) = 0.3.
- Peluang seorang pelanggan yang membeli kue cokelat juga membeli kue keju dapat dihitung dengan rumus: P(B|A) = P(A∩B) / P(A) = 0.3 / 0.6 = 0.5.
Contoh Soal Peluang Kejadian Tidak Saling Lepas (Tingkat Kesulitan Sulit)
Sebuah perusahaan memiliki dua mesin produksi, yaitu mesin A dan mesin B. Mesin A menghasilkan 70% dari total produksi, sedangkan mesin B menghasilkan 30%. Diketahui bahwa 5% dari produksi mesin A cacat, sedangkan 8% dari produksi mesin B cacat. Jika sebuah produk diambil secara acak dari total produksi, tentukan peluang produk tersebut cacat.
- Misalkan C adalah kejadian produk cacat.
- Kita tahu P(A) = 0.7, P(B) = 0.3, P(C|A) = 0.05, dan P(C|B) = 0.08.
- Peluang produk cacat dapat dihitung dengan rumus: P(C) = P(C|A) * P(A) + P(C|B) * P(B) = (0.05 * 0.7) + (0.08 * 0.3) = 0.061.
Pembahasan Soal Peluang Kejadian Tidak Saling Lepas
Pada materi sebelumnya, kita telah mempelajari tentang peluang kejadian saling lepas dan bagaimana menghitungnya. Sekarang, kita akan mempelajari tentang peluang kejadian tidak saling lepas, yaitu kejadian yang memiliki anggota yang sama atau beririsan. Pada kejadian tidak saling lepas, peluang kejadian gabungan dihitung dengan memperhitungkan kemungkinan terjadinya anggota yang sama.
Langkah-Langkah Penyelesaian Soal Peluang Kejadian Tidak Saling Lepas, Contoh soal peluang kejadian tidak saling lepas dan pembahasannya
Untuk menyelesaikan soal peluang kejadian tidak saling lepas, kita dapat menggunakan rumus berikut:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B)
di mana:
- P(A ∪ B) adalah peluang kejadian A atau B
- P(A) adalah peluang kejadian A
- P(B) adalah peluang kejadian B
- P(A ∩ B) adalah peluang kejadian A dan B
Rumus ini menyatakan bahwa peluang kejadian A atau B sama dengan jumlah peluang kejadian A dan B dikurangi peluang kejadian A dan B.
Contoh Soal Peluang Kejadian Tidak Saling Lepas (Tingkat Kesulitan Mudah)
Sebuah kotak berisi 5 bola merah, 3 bola biru, dan 2 bola hijau. Jika diambil satu bola secara acak, tentukan peluang terambilnya bola merah atau bola biru.
Penyelesaian:
Misalkan:
- A adalah kejadian terambilnya bola merah
- B adalah kejadian terambilnya bola biru
Maka:
- P(A) = 5/10 = 1/2
- P(B) = 3/10
- P(A ∩ B) = 0 (karena tidak mungkin terambil bola merah dan biru secara bersamaan)
Jadi, peluang terambilnya bola merah atau bola biru adalah:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 1/2 + 3/10 – 0 = 4/5
Contoh Soal Peluang Kejadian Tidak Saling Lepas (Tingkat Kesulitan Sedang)
Sebuah dadu dilempar dua kali. Tentukan peluang munculnya mata dadu berjumlah 7 atau mata dadu pertama lebih besar dari 4.
Penyelesaian:
Misalkan:
- A adalah kejadian munculnya mata dadu berjumlah 7
- B adalah kejadian mata dadu pertama lebih besar dari 4
Maka:
- P(A) = 6/36 = 1/6 (pasangan mata dadu yang jumlahnya 7: (1,6), (2,5), (3,4), (4,3), (5,2), (6,1))
- P(B) = 12/36 = 1/3 (pasangan mata dadu pertama lebih besar dari 4: (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,1), (6,2), (6,3), (6,4), (6,5), (6,6))
- P(A ∩ B) = 3/36 = 1/12 (pasangan mata dadu yang jumlahnya 7 dan mata dadu pertama lebih besar dari 4: (5,2), (6,1))
Jadi, peluang munculnya mata dadu berjumlah 7 atau mata dadu pertama lebih besar dari 4 adalah:
P(A ∪ B) = P(A) + P(B) – P(A ∩ B) = 1/6 + 1/3 – 1/12 = 1/2
Aplikasi Peluang Kejadian Tidak Saling Lepas dalam Kehidupan Sehari-hari
Peluang kejadian tidak saling lepas seringkali muncul dalam kehidupan sehari-hari. Kejadian tidak saling lepas adalah kejadian yang memiliki kemungkinan terjadi bersamaan. Contohnya, ketika kita melempar sebuah dadu, peluang mendapatkan angka genap dan angka prima tidak saling lepas karena angka 2 dan 6 adalah genap dan prima.
Dalam artikel ini, kita akan menjelajahi beberapa aplikasi peluang kejadian tidak saling lepas dalam berbagai bidang kehidupan.
Aplikasi dalam Bidang Kesehatan
Dalam bidang kesehatan, peluang kejadian tidak saling lepas dapat digunakan untuk menganalisis faktor risiko penyakit. Misalnya, perokok berat memiliki peluang lebih tinggi untuk terkena penyakit jantung dibandingkan dengan bukan perokok. Namun, jika perokok berat juga memiliki riwayat keluarga dengan penyakit jantung, peluang terkena penyakit jantung akan meningkat lebih tinggi lagi. Ini menunjukkan bahwa merokok dan riwayat keluarga merupakan faktor risiko yang tidak saling lepas dalam hal penyakit jantung.
Aplikasi dalam Bidang Ekonomi
Dalam bidang ekonomi, peluang kejadian tidak saling lepas dapat digunakan untuk menganalisis risiko investasi. Misalnya, investor yang menanamkan modal di sektor properti mungkin mempertimbangkan faktor risiko seperti inflasi dan suku bunga. Inflasi dan suku bunga merupakan faktor risiko yang tidak saling lepas dalam hal investasi properti. Kenaikan inflasi dapat menyebabkan penurunan nilai aset properti, sementara kenaikan suku bunga dapat membuat biaya pinjaman untuk membeli properti menjadi lebih mahal.
Aplikasi dalam Bidang Sosial
Dalam bidang sosial, peluang kejadian tidak saling lepas dapat digunakan untuk menganalisis faktor risiko kejahatan. Misalnya, tingkat kejahatan di suatu daerah mungkin dipengaruhi oleh faktor seperti kemiskinan dan pengangguran. Kemiskinan dan pengangguran merupakan faktor risiko yang tidak saling lepas dalam hal kejahatan. Tingkat kemiskinan yang tinggi dapat menyebabkan peningkatan peluang seseorang untuk melakukan kejahatan, sementara tingkat pengangguran yang tinggi dapat membuat orang lebih sulit mendapatkan pekerjaan dan meningkatkan kemungkinan mereka melakukan kejahatan.
Tabel Perbandingan Kejadian Saling Lepas dan Tidak Saling Lepas
Dalam teori peluang, memahami perbedaan antara kejadian saling lepas dan kejadian tidak saling lepas sangat penting untuk menghitung peluang kejadian gabungan. Kejadian saling lepas adalah kejadian yang tidak dapat terjadi bersamaan, sedangkan kejadian tidak saling lepas adalah kejadian yang dapat terjadi bersamaan. Mari kita bahas perbedaan keduanya dengan lebih detail.
Perbandingan Kejadian Saling Lepas dan Tidak Saling Lepas
Berikut tabel perbandingan antara kejadian saling lepas dan kejadian tidak saling lepas:
| Karakteristik | Kejadian Saling Lepas | Kejadian Tidak Saling Lepas |
|---|---|---|
| Definisi | Dua kejadian saling lepas jika kejadian satu tidak mempengaruhi kejadian lainnya. Dengan kata lain, jika satu kejadian terjadi, kejadian lainnya tidak dapat terjadi. | Dua kejadian tidak saling lepas jika kejadian satu dapat mempengaruhi kejadian lainnya. Dengan kata lain, jika satu kejadian terjadi, kejadian lainnya dapat terjadi juga. |
| Rumus |
P(A atau B) = P(A) + P(B) |
P(A atau B) = P(A) + P(B) – P(A dan B) |
| Contoh |
Contohnya, melempar koin dan mendapatkan sisi kepala (A) adalah kejadian saling lepas dengan melempar koin dan mendapatkan sisi ekor (B). Kedua kejadian ini tidak dapat terjadi bersamaan. |
Contohnya, mengambil kartu as dari setumpuk kartu (A) dan mengambil kartu hati dari setumpuk kartu (B) adalah kejadian tidak saling lepas. Kedua kejadian ini dapat terjadi bersamaan, yaitu ketika kartu as hati diambil. |
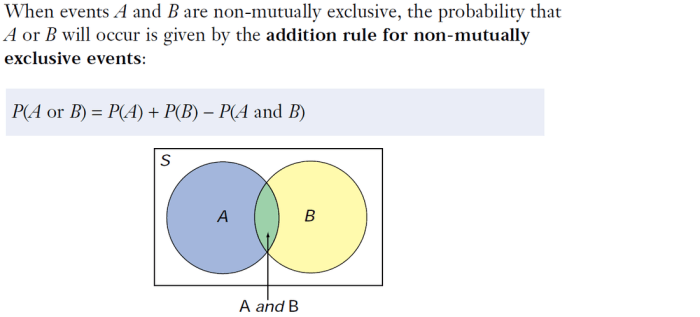
Diagram Venn untuk Kejadian Tidak Saling Lepas
Diagram Venn adalah alat visual yang berguna untuk memahami hubungan antara himpunan atau kejadian. Dalam konteks peluang, diagram Venn dapat membantu kita memvisualisasikan dan menghitung peluang kejadian tidak saling lepas.
Kejadian tidak saling lepas adalah kejadian yang memiliki setidaknya satu elemen yang sama. Artinya, kejadian-kejadian ini dapat terjadi bersamaan. Diagram Venn membantu kita memahami bagaimana kejadian-kejadian ini saling tumpang tindih dan bagaimana probabilitas kejadian gabungan dihitung.
Membuat Diagram Venn untuk Kejadian Tidak Saling Lepas
Diagram Venn untuk kejadian tidak saling lepas terdiri dari dua lingkaran yang saling tumpang tindih. Setiap lingkaran mewakili satu kejadian. Area yang tumpang tindih mewakili kejadian gabungan, yaitu kejadian yang terjadi pada kedua kejadian tersebut.
Sebagai contoh, perhatikan kejadian A dan kejadian B. Kejadian A adalah “mengambil kartu As dari setumpuk kartu” dan kejadian B adalah “mengambil kartu berwarna merah dari setumpuk kartu”. Kejadian A dan B tidak saling lepas karena ada kemungkinan untuk mengambil kartu As berwarna merah.
Diagram Venn untuk kejadian ini akan menunjukkan dua lingkaran yang saling tumpang tindih. Lingkaran A mewakili kejadian “mengambil kartu As”, lingkaran B mewakili kejadian “mengambil kartu berwarna merah”, dan area tumpang tindih mewakili kejadian “mengambil kartu As berwarna merah”.
Memahami Konsep Kejadian Tidak Saling Lepas dengan Diagram Venn
Diagram Venn membantu kita memahami konsep kejadian tidak saling lepas dengan cara berikut:
- Visualisasi Tumpang Tindih: Diagram Venn secara visual menunjukkan bagaimana kejadian tidak saling lepas memiliki area tumpang tindih, yang mewakili kejadian gabungan. Hal ini membantu kita memahami bahwa kejadian-kejadian ini dapat terjadi bersamaan.
- Probabilitas Gabungan: Diagram Venn membantu kita menghitung probabilitas kejadian gabungan dengan mengidentifikasi area tumpang tindih. Probabilitas kejadian gabungan adalah probabilitas bahwa salah satu dari kedua kejadian terjadi.
- Hubungan Antara Kejadian: Diagram Venn membantu kita memahami hubungan antara kejadian-kejadian tidak saling lepas. Kita dapat melihat bagaimana kejadian-kejadian ini saling bergantung dan bagaimana probabilitas satu kejadian dapat memengaruhi probabilitas kejadian lainnya.
Soal Latihan Peluang Kejadian Tidak Saling Lepas
Dalam probabilitas, dua kejadian dikatakan tidak saling lepas jika kedua kejadian tersebut dapat terjadi bersamaan. Artinya, kemungkinan salah satu kejadian terjadi tidak memengaruhi kemungkinan kejadian lainnya. Untuk memahami konsep ini, mari kita coba selesaikan beberapa soal latihan berikut.
Soal Latihan 1: Memilih Bola dari Kantong
Sebuah kantong berisi 5 bola merah, 3 bola biru, dan 2 bola hijau. Jika diambil 2 bola secara acak tanpa pengembalian, tentukan peluang terambilnya 1 bola merah dan 1 bola biru.
- Solusi:
- Kejadian pertama: Terambilnya bola merah. Peluangnya adalah 5/10.
- Kejadian kedua: Terambilnya bola biru setelah bola merah diambil. Karena tidak ada pengembalian, maka peluangnya menjadi 3/9.
- Peluang terambilnya 1 bola merah dan 1 bola biru adalah hasil kali dari kedua peluang tersebut, yaitu (5/10) * (3/9) = 1/6.
Soal Latihan 2: Melempar Dadu
Dua buah dadu dilempar bersamaan. Tentukan peluang munculnya mata dadu 5 pada dadu pertama dan mata dadu genap pada dadu kedua.
- Solusi:
- Kejadian pertama: Munculnya mata dadu 5 pada dadu pertama. Peluangnya adalah 1/6.
- Kejadian kedua: Munculnya mata dadu genap pada dadu kedua. Peluangnya adalah 3/6 = 1/2.
- Peluang munculnya mata dadu 5 pada dadu pertama dan mata dadu genap pada dadu kedua adalah hasil kali dari kedua peluang tersebut, yaitu (1/6) * (1/2) = 1/12.
Soal Latihan 3: Mengambil Kartu dari Dek
Sebuah dek kartu standar berisi 52 kartu. Jika diambil 2 kartu secara acak tanpa pengembalian, tentukan peluang terambilnya 1 kartu As dan 1 kartu King.
- Solusi:
- Kejadian pertama: Terambilnya kartu As. Peluangnya adalah 4/52 = 1/13.
- Kejadian kedua: Terambilnya kartu King setelah kartu As diambil. Karena tidak ada pengembalian, maka peluangnya menjadi 4/51.
- Peluang terambilnya 1 kartu As dan 1 kartu King adalah hasil kali dari kedua peluang tersebut, yaitu (1/13) * (4/51) = 4/663.
Soal Latihan 4: Mengambil Kelereng dari Toples
Sebuah toples berisi 10 kelereng merah, 8 kelereng biru, dan 6 kelereng hijau. Jika diambil 2 kelereng secara acak tanpa pengembalian, tentukan peluang terambilnya 1 kelereng merah dan 1 kelereng biru.
- Solusi:
- Kejadian pertama: Terambilnya kelereng merah. Peluangnya adalah 10/24.
- Kejadian kedua: Terambilnya kelereng biru setelah kelereng merah diambil. Karena tidak ada pengembalian, maka peluangnya menjadi 8/23.
- Peluang terambilnya 1 kelereng merah dan 1 kelereng biru adalah hasil kali dari kedua peluang tersebut, yaitu (10/24) * (8/23) = 10/69.
Soal Latihan 5: Memilih Pelajar dari Kelas
Sebuah kelas berisi 20 pelajar, 12 diantaranya perempuan dan 8 laki-laki. Jika dipilih 2 pelajar secara acak, tentukan peluang terambilnya 1 pelajar perempuan dan 1 pelajar laki-laki.
- Solusi:
- Kejadian pertama: Terambilnya pelajar perempuan. Peluangnya adalah 12/20.
- Kejadian kedua: Terambilnya pelajar laki-laki setelah pelajar perempuan diambil. Karena tidak ada pengembalian, maka peluangnya menjadi 8/19.
- Peluang terambilnya 1 pelajar perempuan dan 1 pelajar laki-laki adalah hasil kali dari kedua peluang tersebut, yaitu (12/20) * (8/19) = 48/380 = 12/95.
Simpulan Akhir
Memahami konsep peluang kejadian tidak saling lepas sangat penting dalam berbagai bidang, seperti statistika, ekonomi, dan ilmu sosial. Dengan memahami konsep ini, kita dapat memprediksi dan menganalisis berbagai peristiwa dengan lebih akurat.




