Contoh soal perkalian bentuk akar – Pernahkah Anda bertanya-tanya bagaimana cara mengalikan bentuk akar? Bentuk akar seringkali muncul dalam berbagai bidang, mulai dari matematika hingga fisika. Memahami konsep perkalian bentuk akar merupakan kunci untuk menyelesaikan berbagai soal dan memahami konsep yang lebih kompleks.
Dalam artikel ini, kita akan menjelajahi dunia perkalian bentuk akar. Anda akan menemukan penjelasan sederhana, contoh soal yang bervariasi, dan langkah-langkah penyelesaian yang mudah dipahami. Siap untuk menaklukkan perkalian bentuk akar? Mari kita mulai!
Pengertian Perkalian Bentuk Akar: Contoh Soal Perkalian Bentuk Akar
Perkalian bentuk akar merupakan operasi matematika yang melibatkan perkalian dua atau lebih bentuk akar. Bentuk akar sendiri adalah suatu bentuk penulisan bilangan yang mengandung tanda akar, misalnya √2, √5, √7, dan seterusnya. Perkalian bentuk akar memiliki aturan dan sifat khusus yang perlu dipahami agar dapat menyelesaikan operasi matematika tersebut dengan benar.
Contoh Perkalian Bentuk Akar
Sebagai contoh, kita dapat melihat perkalian bentuk akar berikut: √2 x √3. Hasil dari perkalian ini adalah √6. Ini karena √2 x √3 sama dengan √(2 x 3) yang hasilnya adalah √6.
Contoh soal perkalian bentuk akar memang cukup sering dijumpai dalam pelajaran matematika. Misalnya, soal seperti “Tentukan hasil dari √2 x √8”. Untuk memahami konsep ini lebih dalam, kamu bisa mencoba mengerjakan contoh soal suku tengah barisan aritmatika, seperti yang ada di link ini.
Konsep barisan aritmatika ini juga bisa diterapkan dalam berbagai macam soal matematika, termasuk soal perkalian bentuk akar.
Prinsip Dasar Perkalian Bentuk Akar
Prinsip dasar perkalian bentuk akar adalah bahwa perkalian dua bentuk akar sama dengan akar dari hasil perkalian kedua bilangan yang berada di bawah tanda akar. Secara matematis, hal ini dapat ditulis sebagai berikut:
√a x √b = √(a x b)
Dimana a dan b adalah bilangan real positif. Prinsip ini berlaku untuk semua bentuk akar, baik itu akar kuadrat, akar kubik, atau akar pangkat lainnya.
Perkalian Bentuk Akar dengan Suku Dua
Perkalian bentuk akar dengan suku dua merupakan operasi matematika yang melibatkan penggabungan dua bentuk aljabar, yaitu bentuk akar dan suku dua. Bentuk akar adalah bilangan yang ditulis dalam bentuk akar kuadrat, seperti √2, √3, atau √5. Sedangkan suku dua adalah bentuk aljabar yang terdiri dari dua suku, seperti 2x + 3 atau 5y – 1.
Cara Mengalikan Bentuk Akar dengan Suku Dua
Untuk mengalikan bentuk akar dengan suku dua, kita dapat menggunakan sifat distributif perkalian. Sifat distributif menyatakan bahwa perkalian suatu bilangan dengan jumlah beberapa bilangan sama dengan jumlah perkalian bilangan tersebut dengan masing-masing bilangan dalam jumlah tersebut.
Misalnya, untuk mengalikan √2 dengan (x + 3), kita dapat mengalikan √2 dengan masing-masing suku dalam (x + 3):
√2 × (x + 3) = (√2 × x) + (√2 × 3) = √2x + 3√2
Dalam hal ini, kita mengalikan √2 dengan x dan √2 dengan 3, dan kemudian menjumlahkan hasilnya.
Contoh Soal
Berikut adalah contoh soal perkalian bentuk akar dengan suku dua:
Hitunglah hasil dari (√3 + 2) × (√5 – 1).
Langkah-langkah Penyelesaian
- Kalikan suku pertama dari bentuk akar dengan setiap suku pada suku dua:
- Kalikan suku kedua dari bentuk akar dengan setiap suku pada suku dua:
- Jumlahkan hasil dari langkah 1 dan langkah 2:
- Gabungkan suku-suku sejenis:
- Kalikan koefisien kedua bentuk akar.
- Kalikan radicand kedua bentuk akar.
- Gabungkan hasil perkalian koefisien dan radicand di bawah tanda akar yang sama.
- Sederhanakan hasil perkalian dengan mengeluarkan faktor sempurna dari radicand.
- Kalikan koefisien kedua bentuk akar. Karena tidak ada koefisien yang tertera, maka koefisiennya dianggap 1, sehingga 1 x 1 = 1.
- Kalikan radicand kedua bentuk akar. √2 x √8 = √(2 x 8) = √16.
- Gabungkan hasil perkalian koefisien dan radicand di bawah tanda akar yang sama. √16.
- Sederhanakan hasil perkalian dengan mengeluarkan faktor sempurna dari radicand. √16 = √(4 x 4) = 4.
√3 × (√5 – 1) = (√3 × √5) – (√3 × 1) = √15 – √3
2 × (√5 – 1) = (2 × √5) – (2 × 1) = 2√5 – 2
(√15 – √3) + (2√5 – 2) = √15 – √3 + 2√5 – 2
√15 + 2√5 – √3 – 2
Jadi, hasil dari (√3 + 2) × (√5 – 1) adalah √15 + 2√5 – √3 – 2.
Perkalian Bentuk Akar dengan Bentuk Akar Lain
Perkalian bentuk akar dengan bentuk akar lain merupakan operasi dasar dalam aljabar yang melibatkan penggabungan dua atau lebih akar. Operasi ini melibatkan pemahaman tentang sifat-sifat akar dan aturan perkalian. Pada dasarnya, perkalian bentuk akar dilakukan dengan mengalikan koefisien dan radicand (bilangan di bawah tanda akar) secara terpisah.
Cara Mengalikan Bentuk Akar dengan Bentuk Akar Lain, Contoh soal perkalian bentuk akar
Untuk mengalikan bentuk akar dengan bentuk akar lain, kita dapat mengikuti langkah-langkah berikut:
Contoh Soal Perkalian Bentuk Akar dengan Bentuk Akar Lain
Misalnya, kita ingin mengalikan √2 dengan √8. Berikut langkah-langkah penyelesaiannya:
Jadi, √2 x √8 = 4.
Contoh Soal Lainnya
Berikut contoh soal lain untuk mengilustrasikan perkalian bentuk akar dengan bentuk akar lain:
| Soal | Langkah Penyelesaian | Hasil |
|---|---|---|
| 2√3 x 3√5 | (2 x 3)√(3 x 5) = 6√15 | 6√15 |
| √7 x √7 | √(7 x 7) = √49 | 7 |
| √12 x √3 | √(12 x 3) = √36 | 6 |
Soal Latihan Perkalian Bentuk Akar
Perkalian bentuk akar merupakan salah satu operasi dasar dalam aljabar yang melibatkan manipulasi akar kuadrat. Menguasai konsep ini penting untuk memahami berbagai operasi aljabar lainnya, terutama dalam menyelesaikan persamaan dan pertidaksamaan yang melibatkan akar kuadrat.
Soal Latihan Perkalian Bentuk Akar
Berikut ini adalah 10 soal latihan perkalian bentuk akar dengan tingkat kesulitan yang bervariasi. Soal-soal ini disusun untuk membantu Anda memahami dan menguasai konsep perkalian bentuk akar.
| No | Soal |
|---|---|
| 1 | √2 x √8 |
| 2 | √3 x √12 |
| 3 | √5 x √20 |
| 4 | √7 x √28 |
| 5 | √11 x √44 |
| 6 | 2√3 x 3√2 |
| 7 | 5√6 x 2√3 |
| 8 | (√2 + √3) x (√2 – √3) |
| 9 | (√5 + √2) x (√5 + √2) |
| 10 | (√7 – √3) x (√7 + √3) |
Kunci Jawaban
Berikut adalah kunci jawaban untuk soal latihan perkalian bentuk akar di atas:
| No | Jawaban |
|---|---|
| 1 | 4 |
| 2 | 6 |
| 3 | 10 |
| 4 | 14 |
| 5 | 22 |
| 6 | 6√6 |
| 7 | 10√18 |
| 8 | -1 |
| 9 | 7 + 2√10 |
| 10 | 4 |
Kesimpulan
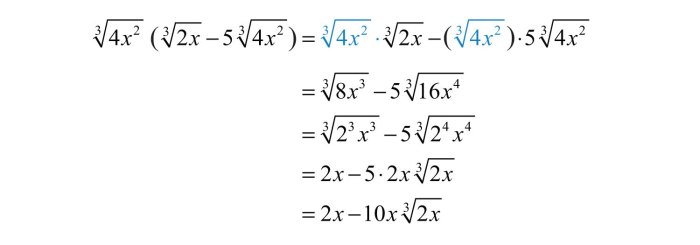
Setelah mempelajari konsep perkalian bentuk akar, Anda telah memiliki alat yang ampuh untuk menyelesaikan berbagai masalah matematika. Ingat, latihan adalah kunci untuk menguasai konsep ini. Jangan ragu untuk mencoba soal-soal latihan yang telah disediakan dan teruslah berlatih agar kemampuan Anda semakin terasah.