Contoh soal persamaan dan pertidaksamaan nilai mutlak – Nilai mutlak, konsep matematika yang mungkin terdengar asing, ternyata memiliki peran penting dalam berbagai bidang, mulai dari ilmu pengetahuan hingga kehidupan sehari-hari. Bayangkan, bagaimana kita bisa menghitung jarak tempuh tanpa melibatkan nilai mutlak? Atau, bagaimana kita bisa memahami perbedaan suhu antara dua tempat tanpa nilai mutlak?
Dalam artikel ini, kita akan menjelajahi dunia nilai mutlak, mulai dari pengertian dasar hingga penerapannya dalam persamaan dan pertidaksamaan. Kita akan mempelajari cara menyelesaikan soal-soal yang melibatkan nilai mutlak dengan mudah dan percaya diri. Siap untuk menguasai konsep ini? Mari kita mulai!
Persamaan Nilai Mutlak
Persamaan nilai mutlak adalah persamaan yang melibatkan fungsi nilai mutlak. Fungsi nilai mutlak, yang dilambangkan dengan tanda “| |”, mengembalikan nilai absolut dari suatu bilangan, yaitu jarak bilangan tersebut dari nol tanpa mempertimbangkan tanda. Dengan kata lain, nilai mutlak dari bilangan selalu positif atau nol.
Pengertian Persamaan Nilai Mutlak
Persamaan nilai mutlak adalah persamaan yang mengandung fungsi nilai mutlak. Fungsi nilai mutlak didefinisikan sebagai:
|x| = x jika x ≥ 0
|x| = -x jika x < 0
Artinya, nilai mutlak dari suatu bilangan x adalah x jika x positif atau nol, dan -x jika x negatif.
Contoh Kasus Persamaan Nilai Mutlak
Misalnya, jika kita ingin mencari nilai x yang memenuhi persamaan |x| = 5, maka kita mencari nilai x yang berjarak 5 satuan dari nol. Ada dua kemungkinan solusi, yaitu x = 5 dan x = -5.
Contoh Soal Persamaan Nilai Mutlak, Contoh soal persamaan dan pertidaksamaan nilai mutlak
Berikut adalah contoh soal persamaan nilai mutlak sederhana:
Tentukan nilai x yang memenuhi persamaan |x – 2| = 3.
Penyelesaian:
1. Menentukan dua kemungkinan:
Karena |x – 2| = 3, maka x – 2 = 3 atau x – 2 = -3.
2. Menyelesaikan persamaan:
Jika x – 2 = 3, maka x = 5.
Contoh soal persamaan dan pertidaksamaan nilai mutlak memang seru, ya! Kamu perlu jeli dalam memahami konsep dasar nilai mutlak, seperti jarak suatu bilangan terhadap nol. Nah, untuk memahami konsep fisika, seperti impuls dan momentum, kamu juga perlu memahami konsep dasar yang mendasarinya.
Misalnya, untuk memahami contoh soal impuls dan momentum, kamu perlu memahami konsep gaya dan perubahan kecepatan, yang bisa dipelajari di contoh soal impuls dan momentum. Sama seperti contoh soal persamaan dan pertidaksamaan nilai mutlak, contoh soal impuls dan momentum juga membutuhkan pemahaman konsep dasar yang kuat untuk menyelesaikannya dengan tepat.
Jika x – 2 = -3, maka x = -1.
3. Solusi:
Jadi, nilai x yang memenuhi persamaan |x – 2| = 3 adalah x = 5 atau x = -1.
Langkah-langkah Menyelesaikan Persamaan Nilai Mutlak
| Langkah | Deskripsi | Contoh |
|---|---|---|
| 1. Menentukan dua kemungkinan | Tuliskan dua persamaan yang mungkin, yaitu dengan tanda positif dan negatif dari nilai mutlak. | |x – 2| = 3 menjadi x – 2 = 3 dan x – 2 = -3 |
| 2. Menyelesaikan persamaan | Selesaikan kedua persamaan yang telah dituliskan. | x – 2 = 3 ⇒ x = 5 x – 2 = -3 ⇒ x = -1 |
| 3. Solusi | Tuliskan solusi dari persamaan nilai mutlak. | Solusi dari |x – 2| = 3 adalah x = 5 atau x = -1 |
Konsep Nilai Mutlak dalam Aljabar Linear
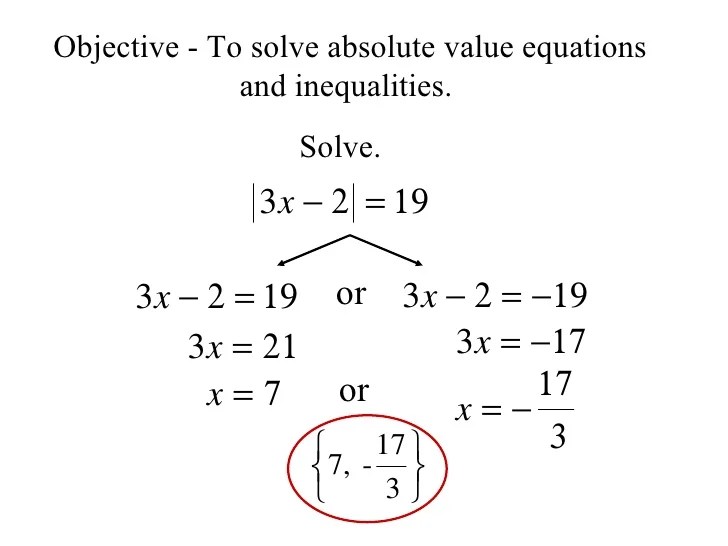
Nilai mutlak, yang sering kita jumpai dalam aljabar dasar, juga memiliki peran penting dalam aljabar linear. Konsep ini meluas ke vektor dan matriks, memungkinkan kita untuk mengukur “besarnya” atau “panjang” dari entitas-entitas aljabar linear ini. Dalam konteks ini, nilai mutlak membantu kita memahami dan menganalisis hubungan antara vektor dan matriks, serta memberikan kerangka kerja untuk mengukur jarak dan sudut dalam ruang vektor.
Nilai Mutlak Vektor
Nilai mutlak dari sebuah vektor, yang sering disebut sebagai “norma” vektor, mewakili panjang atau besarnya vektor tersebut. Dalam ruang vektor, nilai mutlak vektor dihitung menggunakan teorema Pythagoras, dengan mengambil akar kuadrat dari jumlah kuadrat komponen-komponen vektor tersebut.
- Misalnya, untuk vektor v = (3, 4), nilai mutlak atau norma vektor v, ditulis sebagai ||v||, dihitung sebagai:
||v|| = √(32 + 42) = √(9 + 16) = √25 = 5
Jadi, nilai mutlak vektor v adalah 5, yang menunjukkan panjang vektor tersebut.
Nilai Mutlak Matriks
Nilai mutlak dari sebuah matriks, juga dikenal sebagai “norma matriks”, mewakili besarnya atau skala transformasi linear yang diwakili oleh matriks tersebut. Ada berbagai jenis norma matriks, seperti norma Frobenius, norma kolom, dan norma baris, masing-masing dengan definisi dan interpretasi yang berbeda.
- Norma Frobenius, misalnya, dihitung dengan mengambil akar kuadrat dari jumlah kuadrat semua elemen dalam matriks.
- Norma kolom dan norma baris, di sisi lain, mengukur besarnya transformasi linear yang diwakili oleh matriks dengan melihat kolom atau baris matriks tersebut.
Contohnya, untuk matriks:
A = [ 1 2 ]
[ 3 4 ]
Norma Frobenius dari matriks A, ditulis sebagai ||A||F, dihitung sebagai:
||A||F = √(12 + 22 + 32 + 42) = √30
Nilai ini mewakili besarnya transformasi linear yang diwakili oleh matriks A.
Penggunaan Nilai Mutlak dalam Operasi Vektor dan Matriks
Nilai mutlak memainkan peran penting dalam berbagai operasi vektor dan matriks, termasuk:
- Pengukuran Jarak: Nilai mutlak vektor digunakan untuk menghitung jarak antara dua titik dalam ruang vektor. Jarak antara dua titik dapat dihitung dengan mencari nilai mutlak dari selisih vektor yang mewakili kedua titik tersebut.
- Normalisasi Vektor: Nilai mutlak digunakan untuk menormalkan vektor, yaitu mengubah vektor menjadi vektor dengan panjang 1. Vektor yang dinormalisasi sering digunakan dalam berbagai aplikasi, seperti pemrosesan sinyal dan pengenalan pola.
- Pembandingan Vektor: Nilai mutlak dapat digunakan untuk membandingkan panjang atau besarnya dua vektor. Vektor dengan nilai mutlak yang lebih besar memiliki panjang atau besarnya yang lebih besar.
- Pengukuran Stabilitas: Dalam analisis numerik, nilai mutlak digunakan untuk mengukur stabilitas algoritma numerik. Algoritma yang stabil menghasilkan hasil yang sedikit berbeda bahkan ketika inputnya sedikit berubah.
Kesulitan dalam Memahaman Konsep Nilai Mutlak: Contoh Soal Persamaan Dan Pertidaksamaan Nilai Mutlak
Konsep nilai mutlak merupakan salah satu topik dalam matematika yang seringkali menimbulkan kesulitan bagi siswa. Hal ini dikarenakan konsep nilai mutlak memiliki sifat yang unik dan berbeda dengan konsep matematika lainnya. Pemahaman yang mendalam tentang nilai mutlak sangat penting, karena nilai mutlak memiliki aplikasi luas dalam berbagai bidang, seperti fisika, teknik, dan ilmu komputer.
Kesulitan dalam Memahami Definisi Nilai Mutlak
Salah satu kesulitan yang dihadapi siswa adalah memahami definisi nilai mutlak. Nilai mutlak dari suatu bilangan adalah jarak bilangan tersebut dari nol pada garis bilangan. Konsep jarak ini seringkali membuat siswa bingung, terutama ketika dihadapkan dengan bilangan negatif. Siswa mungkin terbiasa dengan konsep jarak sebagai besaran positif, sehingga mereka kesulitan memahami bahwa jarak dari suatu bilangan negatif ke nol juga merupakan besaran positif.
Kesulitan dalam Menerapkan Sifat Nilai Mutlak
Setelah memahami definisi, siswa juga sering mengalami kesulitan dalam menerapkan sifat-sifat nilai mutlak. Sifat-sifat nilai mutlak, seperti |a| = |–a|, |a| ≥ 0, dan |a| = √(a²) dapat digunakan untuk menyelesaikan persamaan dan pertidaksamaan nilai mutlak. Namun, siswa seringkali kesulitan dalam mengingat dan menerapkan sifat-sifat ini secara tepat.
Contoh Kasus Kesulitan dalam Menyelesaikan Soal
Misalnya, dalam menyelesaikan persamaan |x – 2| = 5, siswa mungkin kesulitan memahami bahwa persamaan tersebut memiliki dua solusi, yaitu x = 7 dan x = –3. Hal ini karena mereka mungkin hanya memfokuskan pada satu kemungkinan, yaitu x – 2 = 5, dan mengabaikan kemungkinan lainnya, yaitu x – 2 = –5. Kesulitan serupa juga muncul dalam menyelesaikan pertidaksamaan nilai mutlak, seperti |x + 1| ≤ 3. Siswa mungkin hanya memfokuskan pada satu kasus, yaitu x + 1 ≤ 3, dan mengabaikan kasus lainnya, yaitu x + 1 ≥ –3.
Strategi dan Tips Mengatasi Kesulitan
Untuk mengatasi kesulitan dalam memahami konsep nilai mutlak, berikut beberapa strategi dan tips yang dapat diterapkan:
- Visualisasi dengan Garis Bilangan: Menggunakan garis bilangan untuk memvisualisasikan jarak dari suatu bilangan ke nol dapat membantu siswa memahami konsep nilai mutlak secara lebih intuitif.
- Latihan Soal Beraneka Ragam: Melakukan latihan soal yang bervariasi, mulai dari soal sederhana hingga soal kompleks, dapat membantu siswa memperdalam pemahaman mereka tentang konsep nilai mutlak dan sifat-sifatnya.
- Pemahaman Konsep Jarak: Tekankan kembali pengertian nilai mutlak sebagai jarak dari nol pada garis bilangan. Hal ini dapat membantu siswa memahami mengapa nilai mutlak selalu bernilai positif.
- Mengenal Sifat-Sifat Nilai Mutlak: Siswa perlu menghafal dan memahami sifat-sifat nilai mutlak dengan baik. Mereka juga perlu melatih penerapan sifat-sifat tersebut dalam berbagai soal.
- Pembahasan Soal Secara Menyeluruh: Diskusikan soal-soal yang sulit dengan guru atau teman sekelas. Pembahasan yang mendalam dapat membantu siswa memahami konsep dan solusi yang benar.
Akhir Kata
Dengan memahami konsep nilai mutlak, kita tidak hanya mampu menyelesaikan soal-soal matematika dengan lebih mudah, tetapi juga membuka pintu untuk memahami berbagai fenomena di sekitar kita. Nilai mutlak, ternyata, tidak hanya tentang angka, tetapi juga tentang konsep jarak, perbedaan, dan selisih yang penting dalam berbagai bidang kehidupan.






