Contoh soal pertidaksamaan linear 2 variabel – Pernahkah kamu bertanya-tanya bagaimana matematika bisa membantu dalam menyelesaikan masalah sehari-hari? Salah satu konsep matematika yang menarik dan bermanfaat adalah pertidaksamaan linear dua variabel. Konsep ini memungkinkan kita untuk menganalisis dan menyelesaikan berbagai permasalahan, mulai dari penganggaran keuangan hingga penjadwalan kegiatan.
Dalam artikel ini, kita akan membahas lebih dalam tentang pertidaksamaan linear dua variabel, mulai dari pengertian, cara menyelesaikannya, hingga penerapannya dalam kehidupan nyata. Siapkan dirimu untuk memahami konsep ini dengan lebih baik dan siap untuk mengaplikasikannya dalam berbagai situasi.
Pengertian Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear dua variabel merupakan suatu pernyataan matematika yang menyatakan hubungan tidak sama antara dua variabel, yang masing-masing berpangkat satu, dan dihubungkan dengan tanda pertidaksamaan. Dalam pertidaksamaan ini, terdapat tanda “lebih besar dari” (>), “lebih kecil dari” (<), "lebih besar dari atau sama dengan" (≥), atau "lebih kecil dari atau sama dengan" (≤).
Contoh Pertidaksamaan Linear Dua Variabel
Sebagai contoh, perhatikan pertidaksamaan 2x + 3y > 6. Pertidaksamaan ini menyatakan bahwa nilai 2x + 3y lebih besar dari 6. Variabel x dan y dalam pertidaksamaan ini masing-masing berpangkat satu.
Bentuk Umum Pertidaksamaan Linear Dua Variabel
Bentuk umum pertidaksamaan linear dua variabel adalah:
ax + by > c
di mana a, b, dan c adalah konstanta, dan x dan y adalah variabel. Tanda pertidaksamaan dapat berupa >, <, ≥, atau ≤.
Perbedaan Pertidaksamaan Linear Dua Variabel dan Persamaan Linear Dua Variabel
Perbedaan utama antara pertidaksamaan linear dua variabel dan persamaan linear dua variabel terletak pada tanda yang digunakan. Persamaan linear dua variabel menggunakan tanda sama dengan (=), sedangkan pertidaksamaan linear dua variabel menggunakan tanda pertidaksamaan seperti >, <, ≥, atau ≤.
Persamaan linear dua variabel menghasilkan satu solusi yang mewakili titik tunggal pada bidang kartesius. Sedangkan, pertidaksamaan linear dua variabel memiliki banyak solusi yang direpresentasikan oleh suatu daerah pada bidang kartesius.
Menyelesaikan Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear dua variabel merupakan bentuk aljabar yang melibatkan dua variabel dan tanda pertidaksamaan seperti <, >, ≤, atau ≥. Menyelesaikan pertidaksamaan ini berarti mencari semua pasangan nilai variabel yang memenuhi kondisi yang ditentukan oleh tanda pertidaksamaan.
Langkah-langkah Menyelesaikan Pertidaksamaan Linear Dua Variabel
Berikut adalah langkah-langkah umum untuk menyelesaikan pertidaksamaan linear dua variabel:
- Ubah pertidaksamaan menjadi bentuk persamaan dengan mengganti tanda pertidaksamaan dengan tanda sama dengan (=).
- Tentukan titik potong sumbu x dan sumbu y dari persamaan yang telah diubah.
- Gambar garis yang melalui titik potong tersebut. Garis ini akan membagi bidang koordinat menjadi dua bagian.
- Pilih satu titik yang terletak di salah satu bagian bidang koordinat (bukan di garis). Titik ini disebut titik uji.
- Substitusikan koordinat titik uji ke dalam pertidaksamaan awal.
- Jika pertidaksamaan terpenuhi, maka bagian bidang koordinat yang berisi titik uji merupakan solusi dari pertidaksamaan. Jika tidak terpenuhi, maka bagian bidang koordinat yang lain merupakan solusi.
- Arsir bagian bidang koordinat yang merupakan solusi. Garis yang dibentuk oleh persamaan merupakan bagian dari solusi jika tanda pertidaksamaan menggunakan tanda ≤ atau ≥. Jika menggunakan tanda < atau >, maka garis tidak termasuk dalam solusi.
Contoh Soal dan Penyelesaian, Contoh soal pertidaksamaan linear 2 variabel
Berikut adalah contoh soal dan penyelesaian pertidaksamaan linear dua variabel:
| Soal | Langkah Penyelesaian | Hasil |
|---|---|---|
| 2x + y < 4 | 1. Ubah pertidaksamaan menjadi persamaan: 2x + y = 4 2. Tentukan titik potong sumbu x dan sumbu y: – Titik potong sumbu x: y = 0, maka 2x = 4, sehingga x = 2. Titik potongnya adalah (2, 0) – Titik potong sumbu y: x = 0, maka y = 4. Titik potongnya adalah (0, 4) 3. Gambar garis yang melalui titik potong (2, 0) dan (0, 4). 4. Pilih titik uji (0, 0) yang terletak di bagian bawah garis. 5. Substitusikan titik uji ke dalam pertidaksamaan awal: 2(0) + 0 < 4, sehingga 0 < 4. Pertidaksamaan terpenuhi. 6. Arsir bagian bidang koordinat yang berisi titik uji (0, 0). Garis tidak termasuk dalam solusi karena tanda pertidaksamaan adalah <. |
Solusi dari pertidaksamaan 2x + y < 4 adalah semua titik yang terletak di bawah garis 2x + y = 4. Garis tersebut tidak termasuk dalam solusi. |
Menggambar Grafik Pertidaksamaan Linear Dua Variabel
Setelah memahami konsep pertidaksamaan linear dua variabel, langkah selanjutnya adalah menggambar grafiknya. Grafik ini akan menunjukkan daerah penyelesaian yang memenuhi pertidaksamaan tersebut. Dengan memahami cara menggambar grafik, kamu dapat lebih mudah menyelesaikan masalah yang berkaitan dengan pertidaksamaan linear dua variabel.
Cara Menggambar Grafik Pertidaksamaan Linear Dua Variabel
Untuk menggambar grafik pertidaksamaan linear dua variabel, kamu dapat mengikuti langkah-langkah berikut:
- Ubah pertidaksamaan menjadi persamaan linear.
- Tentukan dua titik yang memenuhi persamaan linear tersebut. Kamu bisa memilih nilai x sembarang, lalu substitusikan ke persamaan untuk mendapatkan nilai y.
- Titik-titik yang diperoleh pada langkah 2 dihubungkan dengan garis lurus. Garis ini merupakan batas dari daerah penyelesaian.
- Tentukan daerah penyelesaian dengan memilih titik uji yang tidak berada di garis batas. Substitusikan koordinat titik uji ke pertidaksamaan awal. Jika pertidaksamaan terpenuhi, maka daerah yang memuat titik uji adalah daerah penyelesaian. Jika tidak terpenuhi, maka daerah yang tidak memuat titik uji adalah daerah penyelesaian.
Contoh Soal dan Gambar Grafik
Misalnya, pertidaksamaan linear dua variabel adalah:
2x + y < 4
Untuk menggambar grafiknya, kita dapat mengikuti langkah-langkah di atas:
- Ubah pertidaksamaan menjadi persamaan linear: 2x + y = 4.
- Tentukan dua titik yang memenuhi persamaan linear tersebut. Misalnya, jika x = 0, maka y = 4. Jika x = 2, maka y = 0. Jadi, kita memperoleh dua titik (0, 4) dan (2, 0).
- Hubungkan kedua titik tersebut dengan garis lurus. Garis ini merupakan batas dari daerah penyelesaian.
- Tentukan daerah penyelesaian dengan memilih titik uji. Misalnya, titik uji (0, 0). Substitusikan koordinat titik uji ke pertidaksamaan awal: 2(0) + 0 < 4. Pertidaksamaan terpenuhi. Jadi, daerah yang memuat titik (0, 0) adalah daerah penyelesaian.
Gambar grafiknya adalah sebagai berikut:
| x | y |
|---|---|
| 0 | 4 |
| 2 | 0 |
Gambar grafik menunjukkan garis lurus yang menghubungkan titik (0, 4) dan (2, 0). Daerah yang berada di bawah garis tersebut merupakan daerah penyelesaian. Hal ini karena titik uji (0, 0) berada di bawah garis dan memenuhi pertidaksamaan awal.
Cara Menentukan Daerah Penyelesaian
Ada dua cara untuk menentukan daerah penyelesaian pertidaksamaan linear dua variabel pada grafik:
- Metode Titik Uji: Pilih titik uji yang tidak berada di garis batas. Substitusikan koordinat titik uji ke pertidaksamaan awal. Jika pertidaksamaan terpenuhi, maka daerah yang memuat titik uji adalah daerah penyelesaian. Jika tidak terpenuhi, maka daerah yang tidak memuat titik uji adalah daerah penyelesaian.
- Metode Arsiran: Arsir daerah yang memenuhi pertidaksamaan. Jika pertidaksamaan menggunakan tanda “<” atau “>”, maka arsir daerah di bawah garis batas. Jika pertidaksamaan menggunakan tanda “≤” atau “≥”, maka arsir daerah di atas garis batas.
Penting untuk memahami cara menggambar grafik pertidaksamaan linear dua variabel. Hal ini akan sangat membantu kamu dalam menyelesaikan masalah-masalah yang berkaitan dengan pertidaksamaan linear dua variabel.
Sistem Pertidaksamaan Linear Dua Variabel
Sistem pertidaksamaan linear dua variabel merupakan kumpulan dari dua atau lebih pertidaksamaan linear yang memiliki dua variabel. Variabel-variabel ini biasanya dilambangkan dengan x dan y. Setiap pertidaksamaan dalam sistem ini merepresentasikan suatu garis pada bidang cartesius, dan daerah penyelesaian dari sistem tersebut adalah daerah yang memenuhi semua pertidaksamaan dalam sistem.
Pengertian Sistem Pertidaksamaan Linear Dua Variabel
Sistem pertidaksamaan linear dua variabel adalah kumpulan dari dua atau lebih pertidaksamaan linear yang memiliki dua variabel, biasanya dilambangkan dengan x dan y. Pertidaksamaan linear ini berbentuk ax + by < c, ax + by > c, ax + by ≤ c, atau ax + by ≥ c, dengan a, b, dan c adalah konstanta.
Contoh Soal Sistem Pertidaksamaan Linear Dua Variabel
Sebagai contoh, perhatikan sistem pertidaksamaan berikut:
x + y ≤ 4
2x – y ≥ 2
Untuk menentukan daerah penyelesaian sistem pertidaksamaan ini, kita dapat mengikuti langkah-langkah berikut:
- Gambar garis yang mewakili setiap pertidaksamaan. Untuk melakukannya, kita dapat mengubah pertidaksamaan menjadi persamaan dengan mengganti tanda pertidaksamaan dengan tanda sama dengan.
- Tentukan daerah yang memenuhi setiap pertidaksamaan. Kita dapat memilih titik uji (x, y) yang tidak terletak pada garis dan substitusikan ke dalam pertidaksamaan. Jika pertidaksamaan terpenuhi, maka daerah yang memuat titik uji tersebut adalah daerah penyelesaian.
- Daerah penyelesaian sistem pertidaksamaan adalah irisan dari semua daerah penyelesaian pertidaksamaan dalam sistem.
Berikut adalah contoh gambar daerah penyelesaian sistem pertidaksamaan di atas:
[Gambar daerah penyelesaian sistem pertidaksamaan]
Diagram Venn untuk Menunjukkan Daerah Penyelesaian
Diagram Venn dapat digunakan untuk menunjukkan daerah penyelesaian sistem pertidaksamaan linear dua variabel. Setiap pertidaksamaan dalam sistem direpresentasikan oleh lingkaran pada diagram Venn. Daerah penyelesaian sistem adalah daerah yang berada di dalam semua lingkaran.
[Gambar diagram Venn yang menunjukkan daerah penyelesaian sistem pertidaksamaan]
Penerapan Pertidaksamaan Linear Dua Variabel dalam Kehidupan Sehari-hari
Pertidaksamaan linear dua variabel, meskipun tampak rumit, memiliki banyak aplikasi praktis dalam kehidupan sehari-hari. Konsep ini membantu kita dalam pengambilan keputusan, perencanaan, dan bahkan optimasi sumber daya.
Penganggaran
Pertidaksamaan linear dua variabel dapat digunakan untuk membuat model penganggaran sederhana. Misalnya, kita ingin membeli beberapa buku dan pensil dengan total anggaran Rp 100.000. Harga satu buku Rp 10.000 dan harga satu pensil Rp 5.000.
Kita bisa membuat model matematika sebagai berikut:
Misalkan:
* x = jumlah buku
* y = jumlah pensil
Maka pertidaksamaan linearnya adalah:
10.000x + 5.000y ≤ 100.000
Pertidaksamaan ini menunjukkan bahwa total biaya pembelian buku dan pensil tidak boleh melebihi Rp 100.000. Dengan menggunakan pertidaksamaan ini, kita dapat menentukan berbagai kombinasi jumlah buku dan pensil yang dapat dibeli dengan anggaran yang tersedia.
Penjadwalan
Pertidaksamaan linear dua variabel juga dapat membantu dalam penjadwalan. Misalnya, kita ingin membuat jadwal untuk mengerjakan dua tugas, yaitu mengerjakan tugas A dan tugas B. Waktu yang dibutuhkan untuk mengerjakan tugas A adalah 2 jam dan waktu yang dibutuhkan untuk mengerjakan tugas B adalah 3 jam. Kita hanya memiliki waktu 8 jam untuk menyelesaikan kedua tugas tersebut.
Kita bisa membuat model matematika sebagai berikut:
Misalkan:
* x = waktu yang dialokasikan untuk tugas A (dalam jam)
* y = waktu yang dialokasikan untuk tugas B (dalam jam)
Maka pertidaksamaan linearnya adalah:
2x + 3y ≤ 8
Pertidaksamaan ini menunjukkan bahwa total waktu yang dibutuhkan untuk mengerjakan kedua tugas tidak boleh melebihi 8 jam. Dengan menggunakan pertidaksamaan ini, kita dapat menentukan berbagai kombinasi waktu yang dapat dialokasikan untuk setiap tugas agar keduanya dapat diselesaikan dalam waktu yang tersedia.
Optimasi
Pertidaksamaan linear dua variabel dapat digunakan untuk memodelkan dan menyelesaikan masalah optimasi. Misalnya, sebuah perusahaan ingin memaksimalkan keuntungan dari penjualan dua jenis produk, yaitu produk A dan produk B. Keuntungan dari penjualan satu unit produk A adalah Rp 50.000 dan keuntungan dari penjualan satu unit produk B adalah Rp 30.000. Perusahaan hanya memiliki kapasitas produksi untuk menghasilkan maksimal 100 unit produk A dan 150 unit produk B.
Kita bisa membuat model matematika sebagai berikut:
Misalkan:
* x = jumlah unit produk A yang diproduksi
* y = jumlah unit produk B yang diproduksi
Maka fungsi tujuannya adalah:
Z = 50.000x + 30.000y (memaksimalkan keuntungan)
Keterbatasannya adalah:
x ≤ 100 (kapasitas produksi produk A)
y ≤ 150 (kapasitas produksi produk B)
Dengan menggunakan pertidaksamaan linear dan teknik pemrograman linear, perusahaan dapat menentukan kombinasi jumlah produk A dan produk B yang harus diproduksi untuk memaksimalkan keuntungannya.
Contoh Soal Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear dua variabel merupakan bentuk aljabar yang melibatkan dua variabel dan tanda pertidaksamaan (<, >, ≤, ≥). Untuk menyelesaikan pertidaksamaan linear dua variabel, kita perlu memahami konsep garis batas, daerah penyelesaian, dan metode uji titik.
Berikut ini adalah beberapa contoh soal pertidaksamaan linear dua variabel dengan tingkat kesulitan yang berbeda, lengkap dengan petunjuk dan contoh penyelesaiannya:
Contoh Soal dan Penyelesaian, Contoh soal pertidaksamaan linear 2 variabel
| Nomor | Soal | Petunjuk |
|---|---|---|
| 1 | Tentukan daerah penyelesaian dari pertidaksamaan x + 2y ≤ 4. | 1. Ubah pertidaksamaan menjadi persamaan: x + 2y = 4. 2. Tentukan dua titik pada garis tersebut dengan memberikan nilai sembarang untuk x atau y. Misalnya, jika x = 0, maka y = 2. Jika y = 0, maka x = 4. 3. Gambar garis yang melalui kedua titik tersebut. Garis ini disebut garis batas. 4. Gunakan metode uji titik untuk menentukan daerah penyelesaian. Ambil titik (0,0) yang tidak berada pada garis batas. Substitusikan nilai x dan y ke dalam pertidaksamaan awal. Jika hasil yang diperoleh benar, maka daerah yang memuat titik (0,0) adalah daerah penyelesaian. Jika hasil yang diperoleh salah, maka daerah yang tidak memuat titik (0,0) adalah daerah penyelesaian. 5. Arsir daerah penyelesaian. |
| 2 | Sebuah toko roti membuat dua jenis kue, yaitu kue A dan kue B. Kue A membutuhkan 2 kg tepung dan 1 kg gula, sedangkan kue B membutuhkan 1 kg tepung dan 2 kg gula. Toko roti tersebut memiliki persediaan 10 kg tepung dan 8 kg gula. Buatlah model matematika untuk menentukan jumlah kue A dan kue B yang dapat dibuat toko roti tersebut. | 1. Misalkan x adalah jumlah kue A dan y adalah jumlah kue B. 2. Buatlah sistem pertidaksamaan linear berdasarkan informasi yang diberikan: – Pertidaksamaan untuk tepung: 2x + y ≤ 10 – Pertidaksamaan untuk gula: x + 2y ≤ 8 – Pertidaksamaan untuk jumlah kue: x ≥ 0 dan y ≥ 0 3. Model matematika yang diperoleh adalah: 2x + y ≤ 10 x + 2y ≤ 8 x ≥ 0 y ≥ 0 |
| 3 | Tentukan nilai maksimum dari fungsi objektif Z = 3x + 2y dengan kendala: x + y ≤ 5 x ≥ 0 y ≥ 0 |
1. Gambar daerah penyelesaian dari sistem pertidaksamaan. 2. Tentukan titik-titik sudut dari daerah penyelesaian. 3. Substitusikan nilai x dan y dari setiap titik sudut ke dalam fungsi objektif Z. 4. Nilai maksimum dari Z adalah nilai terbesar yang diperoleh dari langkah 3. |
| 4 | Seorang pedagang menjual dua jenis buah, yaitu apel dan jeruk. Harga 1 kg apel adalah Rp 10.000 dan harga 1 kg jeruk adalah Rp 8.000. Pedagang tersebut ingin memperoleh keuntungan minimal Rp 100.000 dari penjualan kedua jenis buah tersebut. Buatlah model matematika untuk menentukan jumlah apel dan jeruk yang harus dijual pedagang tersebut. | 1. Misalkan x adalah jumlah apel (kg) dan y adalah jumlah jeruk (kg). 2. Buatlah pertidaksamaan berdasarkan informasi yang diberikan: – Pertidaksamaan untuk keuntungan: 10.000x + 8.000y ≥ 100.000 – Pertidaksamaan untuk jumlah buah: x ≥ 0 dan y ≥ 0 3. Model matematika yang diperoleh adalah: 10.000x + 8.000y ≥ 100.000 x ≥ 0 y ≥ 0 |
| 5 | Tentukan daerah penyelesaian dari sistem pertidaksamaan: 2x + y ≤ 6 x – y ≥ 1 x ≥ 0 y ≥ 0 |
1. Gambar garis batas untuk setiap pertidaksamaan. 2. Gunakan metode uji titik untuk menentukan daerah penyelesaian setiap pertidaksamaan. 3. Daerah penyelesaian dari sistem pertidaksamaan adalah irisan dari daerah penyelesaian setiap pertidaksamaan. |
Menentukan Titik Potong Grafik Pertidaksamaan
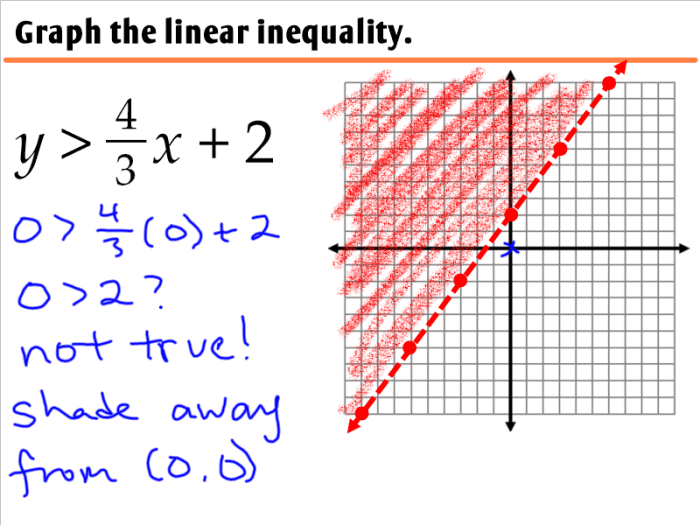
Menentukan titik potong grafik pertidaksamaan linear dua variabel dengan sumbu x dan sumbu y merupakan langkah penting dalam memahami dan menggambar grafik pertidaksamaan. Titik potong ini membantu kita menentukan batas-batas daerah penyelesaian pertidaksamaan tersebut.
Cara Menentukan Titik Potong
Untuk menentukan titik potong grafik pertidaksamaan dengan sumbu x dan sumbu y, kita perlu memahami konsep berikut:
- Titik potong dengan sumbu x: Titik potong dengan sumbu x terjadi ketika nilai y = 0. Untuk menentukannya, kita substitusikan y = 0 ke dalam persamaan pertidaksamaan dan selesaikan untuk nilai x.
- Titik potong dengan sumbu y: Titik potong dengan sumbu y terjadi ketika nilai x = 0. Untuk menentukannya, kita substitusikan x = 0 ke dalam persamaan pertidaksamaan dan selesaikan untuk nilai y.
Contoh Soal
Misalkan kita memiliki pertidaksamaan 2x + 3y ≤ 6. Mari kita tentukan titik potongnya dengan sumbu x dan sumbu y:
Titik Potong dengan Sumbu x
Substitusikan y = 0 ke dalam pertidaksamaan:
2x + 3(0) ≤ 6
Selesaikan untuk x:
2x ≤ 6
x ≤ 3
Jadi, titik potong dengan sumbu x adalah (3, 0).
Titik Potong dengan Sumbu y
Substitusikan x = 0 ke dalam pertidaksamaan:
2(0) + 3y ≤ 6
Selesaikan untuk y:
3y ≤ 6
y ≤ 2
Jadi, titik potong dengan sumbu y adalah (0, 2).
Contoh soal pertidaksamaan linear 2 variabel biasanya melibatkan dua variabel yang dihubungkan oleh tanda pertidaksamaan, seperti “lebih besar dari” atau “lebih kecil dari”. Untuk memahami konsep ini, kamu bisa melihat berbagai contoh soal persamaan dan pertidaksamaan linear di situs ini.
Di sana, kamu akan menemukan contoh soal yang mencakup persamaan dan pertidaksamaan linear, yang bisa membantumu memahami perbedaan dan kesamaan antara keduanya. Setelah memahami konsep dasar, kamu akan lebih mudah menyelesaikan contoh soal pertidaksamaan linear 2 variabel yang lebih kompleks.
Ilustrasi Gambar
Gambar di bawah ini menunjukkan titik potong grafik pertidaksamaan 2x + 3y ≤ 6 dengan sumbu x dan sumbu y:
[Gambar ilustrasi titik potong grafik pertidaksamaan dengan sumbu x dan sumbu y]
Gambar tersebut menunjukkan titik potong dengan sumbu x pada titik (3, 0) dan titik potong dengan sumbu y pada titik (0, 2). Titik-titik ini membantu kita menentukan batas-batas daerah penyelesaian pertidaksamaan.
Menentukan Daerah Penyelesaian
Setelah mendapatkan pertidaksamaan linear dua variabel, langkah selanjutnya adalah menentukan daerah penyelesaiannya. Daerah penyelesaian merupakan himpunan titik-titik yang memenuhi semua pertidaksamaan dalam sistem pertidaksamaan. Ada beberapa metode untuk menentukan daerah penyelesaian, salah satunya adalah metode uji titik.
Metode Uji Titik
Metode uji titik merupakan cara yang mudah untuk menentukan daerah penyelesaian pertidaksamaan linear dua variabel. Cara kerjanya adalah dengan memilih sebuah titik yang tidak terletak pada garis pertidaksamaan, lalu substitusikan titik tersebut ke dalam pertidaksamaan. Jika pertidaksamaan terpenuhi, maka titik tersebut berada di daerah penyelesaian. Jika pertidaksamaan tidak terpenuhi, maka titik tersebut berada di luar daerah penyelesaian.
Contoh Soal dan Langkah-langkah
Misalkan kita diberikan pertidaksamaan x + 2y ≤ 4. Berikut langkah-langkah menentukan daerah penyelesaiannya dengan metode uji titik:
- Tentukan garis pertidaksamaan. Garis pertidaksamaan diperoleh dengan mengubah tanda pertidaksamaan menjadi tanda sama dengan. Dalam contoh ini, garis pertidaksamaan adalah x + 2y = 4.
- Gambar garis pertidaksamaan. Untuk menggambar garis, kita bisa mencari dua titik yang terletak pada garis tersebut. Misalnya, jika x = 0, maka y = 2, dan jika y = 0, maka x = 4. Jadi, kita dapatkan dua titik (0, 2) dan (4, 0) yang dapat kita gunakan untuk menggambar garis.
- Pilih titik uji. Pilih sebuah titik yang tidak terletak pada garis pertidaksamaan. Misalnya, kita pilih titik (0, 0).
- Substitusikan titik uji ke dalam pertidaksamaan. Substitusikan titik (0, 0) ke dalam pertidaksamaan x + 2y ≤ 4. Kita dapatkan 0 + 2(0) ≤ 4, yang merupakan pernyataan benar.
- Tentukan daerah penyelesaian. Karena titik uji (0, 0) memenuhi pertidaksamaan, maka daerah penyelesaian adalah daerah yang memuat titik (0, 0). Daerah penyelesaian ini dapat diwarnai dengan warna yang berbeda untuk menunjukkannya.
Ilustrasi Gambar
Ilustrasi gambar di bawah ini menunjukkan daerah penyelesaian pertidaksamaan x + 2y ≤ 4. Garis x + 2y = 4 diwakili oleh garis putus-putus karena tanda pertidaksamaan adalah “≤”. Titik uji (0, 0) berada di dalam daerah penyelesaian yang diarsir dengan warna biru.
Gambar daerah penyelesaian pertidaksamaan x + 2y ≤ 4:
[Gambar: Garis putus-putus x + 2y = 4 dengan titik (0, 2) dan (4, 0). Daerah penyelesaian diarsir dengan warna biru, dan titik uji (0, 0) berada di dalam daerah penyelesaian.]
Soal Cerita Pertidaksamaan Linear Dua Variabel
Pertidaksamaan linear dua variabel merupakan salah satu materi dalam matematika yang seringkali muncul dalam soal cerita. Soal cerita ini biasanya berkaitan dengan masalah sehari-hari yang melibatkan dua variabel yang saling terkait. Untuk menyelesaikan soal cerita pertidaksamaan linear dua variabel, kita perlu memahami konsep pertidaksamaan linear dan bagaimana mengaplikasikannya dalam konteks cerita.
Langkah-langkah Menyelesaikan Soal Cerita Pertidaksamaan Linear Dua Variabel
Untuk menyelesaikan soal cerita pertidaksamaan linear dua variabel, kita dapat mengikuti langkah-langkah berikut:
- Membuat model matematika: Langkah pertama adalah menerjemahkan soal cerita ke dalam model matematika. Ini berarti mengidentifikasi variabel-variabel yang terlibat dan hubungan antara variabel tersebut dalam bentuk pertidaksamaan.
- Menentukan daerah penyelesaian: Setelah mendapatkan model matematika, kita perlu menentukan daerah penyelesaian dari pertidaksamaan tersebut. Daerah penyelesaian merupakan himpunan titik-titik yang memenuhi pertidaksamaan.
- Mencari solusi: Solusi dari soal cerita pertidaksamaan linear dua variabel adalah titik-titik yang berada di daerah penyelesaian dan memenuhi semua kondisi yang diberikan dalam soal cerita.
Contoh Soal Cerita
Sebuah toko kue ingin membuat dua jenis kue, yaitu kue cokelat dan kue vanila. Setiap kue cokelat membutuhkan 2 butir telur dan 100 gram tepung, sedangkan setiap kue vanila membutuhkan 1 butir telur dan 50 gram tepung. Toko kue tersebut memiliki persediaan 12 butir telur dan 500 gram tepung. Berapa banyak kue cokelat dan kue vanila yang dapat dibuat toko kue tersebut?
Langkah-langkah Penyelesaian
- Membuat model matematika:
- Misalkan x adalah jumlah kue cokelat yang dibuat.
- Misalkan y adalah jumlah kue vanila yang dibuat.
- Pertidaksamaan untuk jumlah telur: 2x + y ≤ 12
- Pertidaksamaan untuk jumlah tepung: 100x + 50y ≤ 500
- Menentukan daerah penyelesaian:
- Gambar garis 2x + y = 12 dan 100x + 50y = 500 pada bidang cartesius.
- Tentukan daerah yang memenuhi pertidaksamaan 2x + y ≤ 12 dan 100x + 50y ≤ 500. Daerah ini adalah daerah penyelesaian.
- Mencari solusi:
- Titik-titik yang berada di daerah penyelesaian dan memiliki koordinat bulat positif merupakan solusi dari soal cerita. Misalnya, titik (3, 4) merupakan solusi karena 3 kue cokelat dan 4 kue vanila dapat dibuat dengan menggunakan 12 butir telur dan 500 gram tepung.
Kesimpulan
Dari contoh soal cerita di atas, dapat disimpulkan bahwa soal cerita pertidaksamaan linear dua variabel dapat diselesaikan dengan membuat model matematika, menentukan daerah penyelesaian, dan mencari solusi yang memenuhi semua kondisi yang diberikan dalam soal cerita.
Simpulan Akhir: Contoh Soal Pertidaksamaan Linear 2 Variabel
Dengan memahami pertidaksamaan linear dua variabel, kita tidak hanya membuka pintu menuju pemahaman matematika yang lebih dalam, tetapi juga menemukan alat yang bermanfaat untuk menyelesaikan masalah sehari-hari. Melalui contoh soal dan penerapannya, kita dapat melihat bagaimana konsep ini dapat membantu kita dalam membuat keputusan yang lebih tepat dan efektif. Jadi, jangan ragu untuk terus mempelajari dan mempraktikkan konsep ini untuk meraih hasil yang optimal dalam berbagai aspek kehidupan.





