Contoh soal pertidaksamaan rasional – Pertidaksamaan rasional, sebuah konsep matematika yang menggabungkan aljabar dan pertidaksamaan, menawarkan tantangan dan peluang menarik untuk mengasah kemampuan berpikir kritis kita. Bayangkan sebuah situasi di mana Anda ingin menentukan rentang nilai yang memenuhi syarat tertentu, namun persyaratan tersebut melibatkan pecahan aljabar. Di sinilah pertidaksamaan rasional memainkan perannya.
Dalam artikel ini, kita akan menyelami dunia pertidaksamaan rasional dengan membahas definisinya, metode penyelesaiannya, dan berbagai contoh soal yang akan membantu Anda memahami konsep ini dengan lebih baik. Siap untuk berpetualang dalam dunia matematika yang penuh teka-teki? Mari kita mulai!
Pengertian Pertidaksamaan Rasional: Contoh Soal Pertidaksamaan Rasional
Pertidaksamaan rasional adalah pertidaksamaan yang melibatkan rasio atau pembagian dua ekspresi aljabar, di mana setidaknya satu ekspresi mengandung variabel. Pertidaksamaan ini memiliki bentuk umum:
f(x) / g(x) > 0, f(x) / g(x) < 0, f(x) / g(x) ≥ 0, atau f(x) / g(x) ≤ 0
dengan f(x) dan g(x) adalah ekspresi aljabar, dan g(x) ≠ 0.
Contoh Pertidaksamaan Rasional
Perhatikan contoh pertidaksamaan rasional berikut:
(x + 2) / (x – 1) > 0
Pertidaksamaan ini melibatkan rasio dua ekspresi aljabar, yaitu (x + 2) dan (x – 1), di mana x adalah variabel. Pertidaksamaan ini menunjukkan bahwa rasio (x + 2) / (x – 1) harus lebih besar dari nol.
Perbedaan Pertidaksamaan Linear dan Pertidaksamaan Rasional
Pertidaksamaan linear dan pertidaksamaan rasional memiliki perbedaan mendasar dalam bentuk dan cara penyelesaiannya.
| Aspek | Pertidaksamaan Linear | Pertidaksamaan Rasional |
|---|---|---|
| Bentuk Umum | ax + b > 0, ax + b < 0, ax + b ≥ 0, atau ax + b ≤ 0 | f(x) / g(x) > 0, f(x) / g(x) < 0, f(x) / g(x) ≥ 0, atau f(x) / g(x) ≤ 0 |
| Contoh | 2x + 3 > 5 | (x + 2) / (x – 1) > 0 |
| Penyelesaian | Menggunakan operasi aljabar sederhana | Melibatkan analisis tanda dan diagram garis bilangan |
Ilustrasi Perbedaan
Pertidaksamaan linear, seperti 2x + 3 > 5, dapat diilustrasikan sebagai garis lurus pada bidang koordinat. Solusi dari pertidaksamaan ini adalah semua titik yang terletak di atas garis lurus tersebut.
Sebaliknya, pertidaksamaan rasional, seperti (x + 2) / (x – 1) > 0, dapat diilustrasikan sebagai kurva pada bidang koordinat. Solusi dari pertidaksamaan ini adalah semua titik yang terletak di atas kurva dan di bawah kurva, tergantung pada tanda pertidaksamaan.
Menyelesaikan Pertidaksamaan Rasional
Pertidaksamaan rasional adalah pertidaksamaan yang melibatkan pecahan aljabar, di mana pembilang dan penyebutnya adalah ekspresi aljabar. Menyelesaikan pertidaksamaan rasional melibatkan langkah-langkah khusus untuk menentukan nilai variabel yang memenuhi pertidaksamaan tersebut.
Langkah-langkah Umum dalam Menyelesaikan Pertidaksamaan Rasional
Langkah-langkah umum dalam menyelesaikan pertidaksamaan rasional adalah sebagai berikut:
- Tentukan nilai-nilai variabel yang membuat penyebut nol. Nilai-nilai ini harus dikecualikan dari solusi karena akan membuat pecahan tak terdefinisi.
- Tentukan nilai-nilai variabel yang membuat pembilang nol. Nilai-nilai ini merupakan titik-titik kritis yang akan membagi garis bilangan menjadi interval-interval.
- Buat garis bilangan dan tandai titik-titik kritis dan nilai-nilai yang dikecualikan.
- Pilih satu nilai dari setiap interval dan substitusikan ke dalam pertidaksamaan asli. Periksa tanda pertidaksamaan untuk setiap interval.
- Tentukan interval-interval yang memenuhi pertidaksamaan. Tulis solusi dalam bentuk notasi interval.
Contoh Soal Pertidaksamaan Rasional
Misalkan kita ingin menyelesaikan pertidaksamaan rasional berikut:
(x + 2) / (x – 1) ≤ 3
Berikut langkah-langkah penyelesaiannya:
- Penyebut nol ketika x = 1. Jadi, x = 1 dikecualikan dari solusi.
- Pembilang nol ketika x = -2. Jadi, x = -2 merupakan titik kritis.
- Buat garis bilangan dan tandai x = -2 dan x = 1.
- Pilih nilai dari setiap interval dan substitusikan ke dalam pertidaksamaan. Misalnya, untuk interval x < -2, kita bisa memilih x = -3. Substitusikan x = -3 ke dalam pertidaksamaan, kita dapatkan:
(-3 + 2) / (-3 – 1) ≤ 3
-1 / -4 ≤ 3
1/4 ≤ 3
Pertidaksamaan terpenuhi. Jadi, interval x < -2 memenuhi pertidaksamaan. Ulangi langkah ini untuk interval lainnya.
- Setelah memeriksa semua interval, kita dapatkan solusi:
x ∈ (-∞, -2] ∪ (1, ∞)
Diagram Alur Penyelesaian Pertidaksamaan Rasional
Berikut diagram alur penyelesaian pertidaksamaan rasional:
- Tentukan nilai-nilai yang membuat penyebut nol. Nilai-nilai ini harus dikecualikan dari solusi.
- Tentukan nilai-nilai yang membuat pembilang nol. Nilai-nilai ini merupakan titik-titik kritis.
- Buat garis bilangan dan tandai titik-titik kritis dan nilai-nilai yang dikecualikan.
- Pilih satu nilai dari setiap interval dan substitusikan ke dalam pertidaksamaan asli.
- Periksa tanda pertidaksamaan untuk setiap interval.
- Tentukan interval-interval yang memenuhi pertidaksamaan.
- Tulis solusi dalam bentuk notasi interval.
Metode Faktorisasi
Metode faktorisasi adalah salah satu cara untuk menyelesaikan pertidaksamaan rasional. Metode ini memanfaatkan sifat faktor-faktor dari polinomial untuk menentukan tanda dari ekspresi rasional pada rentang nilai tertentu.
Langkah-Langkah Metode Faktorisasi
Metode faktorisasi ini dapat diterapkan untuk menyelesaikan pertidaksamaan rasional dengan langkah-langkah berikut:
- Pindahkan semua suku ke ruas kiri pertidaksamaan sehingga ruas kanan menjadi nol.
- Faktorkan pembilang dan penyebut dari ekspresi rasional di ruas kiri.
- Tentukan titik-titik kritis, yaitu nilai-nilai x yang membuat pembilang atau penyebut bernilai nol.
- Buatlah tabel tanda untuk menentukan tanda ekspresi rasional pada setiap interval yang dibentuk oleh titik-titik kritis.
- Tentukan solusi pertidaksamaan berdasarkan tanda ekspresi rasional dan jenis pertidaksamaan (>, <, ≥, ≤).
Contoh Soal
Sebagai contoh, mari kita selesaikan pertidaksamaan rasional berikut:
$\fracx^2 – 4x + 1 > 0$
- Ruas kanan sudah nol.
- Faktorkan pembilang dan penyebut:
$\frac(x + 2)(x – 2)x + 1 > 0$
- Titik-titik kritis adalah x = -2, x = 2, dan x = -1.
- Buat tabel tanda:
Interval x + 2 x – 2 x + 1 $\frac(x + 2)(x – 2)x + 1$ x < -2 – – – – -2 < x < -1 + – – + -1 < x < 2 + – + – x > 2 + + + + - Karena pertidaksamaan adalah “>” (lebih besar dari), maka solusi pertidaksamaan adalah interval di mana ekspresi rasional bernilai positif:
x ∈ (-2, -1) ∪ (2, ∞)
Contoh Soal Pertidaksamaan Rasional
Pertidaksamaan rasional adalah pertidaksamaan yang melibatkan variabel dalam bentuk pecahan. Pecahan tersebut terdiri dari dua ekspresi aljabar, dengan satu ekspresi di pembilang dan yang lainnya di penyebut. Pertidaksamaan rasional sering muncul dalam berbagai bidang, seperti matematika, fisika, dan ekonomi. Memahami konsep pertidaksamaan rasional dan cara menyelesaikannya sangat penting untuk memecahkan masalah yang melibatkan variabel yang terdefinisi dalam bentuk pecahan.
Untuk menyelesaikan pertidaksamaan rasional, kita perlu memperhatikan nilai-nilai yang membuat penyebut nol dan nilai-nilai yang membuat ekspresi dalam pertidaksamaan nol. Nilai-nilai ini akan membagi garis bilangan menjadi beberapa interval, dan kita perlu memeriksa tanda pertidaksamaan pada setiap interval. Berikut adalah contoh soal pertidaksamaan rasional yang dapat membantu Anda memahami konsep ini.
Contoh Soal Pertidaksamaan Rasional dengan Tingkat Kesulitan Berbeda
Berikut adalah 5 contoh soal pertidaksamaan rasional dengan tingkat kesulitan yang berbeda:
-
Tentukan himpunan penyelesaian dari pertidaksamaan
x + 2 / x – 1 > 0
-
Tentukan himpunan penyelesaian dari pertidaksamaan
2x – 1 / x^2 – 4 ≤ 0
-
Tentukan himpunan penyelesaian dari pertidaksamaan
x^2 – 3x + 2 / x^2 – 4x + 3 ≥ 1
-
Tentukan himpunan penyelesaian dari pertidaksamaan
(x + 1) / (x – 2) + (x – 3) / (x + 2) > 0
-
Tentukan himpunan penyelesaian dari pertidaksamaan
(x^2 – 4) / (x^2 + 4) ≤ 1
Contoh Soal Pertidaksamaan Rasional yang Melibatkan Nilai Mutlak
Berikut adalah contoh soal pertidaksamaan rasional yang melibatkan nilai mutlak:
Tentukan himpunan penyelesaian dari pertidaksamaan
|x – 1| / (x + 2) ≤ 2
Contoh Soal Pertidaksamaan Rasional yang Melibatkan Fungsi Pecahan
Berikut adalah contoh soal pertidaksamaan rasional yang melibatkan fungsi pecahan:
Misalkan f(x) = (x + 1) / (x – 2). Tentukan nilai x yang memenuhi pertidaksamaan f(x) > 1.
Kesalahan Umum
Pertidaksamaan rasional memang terlihat rumit, tapi dengan memahami konsep dasar dan menghindari kesalahan umum, kamu bisa menyelesaikannya dengan mudah. Nah, di bagian ini kita akan membahas beberapa kesalahan yang sering terjadi saat menyelesaikan pertidaksamaan rasional dan bagaimana cara menghindarinya.
Tidak Menentukan Titik Kritis
Titik kritis adalah nilai-nilai yang membuat penyebut pertidaksamaan sama dengan nol atau membuat nilai pertidaksamaan sama dengan nol. Titik kritis sangat penting karena membagi sumbu bilangan menjadi interval-interval yang berbeda, di mana tanda pertidaksamaan bisa berubah.
Jika kamu tidak menentukan titik kritis dengan benar, kamu bisa salah menentukan interval yang memenuhi pertidaksamaan.
Contoh Kesalahan, Contoh soal pertidaksamaan rasional
Misalnya, perhatikan pertidaksamaan berikut:
\[\fracx – 2x + 1 > 0\]
Titik kritisnya adalah x = 2 (pembilang sama dengan nol) dan x = -1 (penyebut sama dengan nol). Jika kamu tidak menentukan titik kritis dengan benar, kamu mungkin akan mengabaikan interval yang memenuhi pertidaksamaan.
Cara Menghindari Kesalahan
- Selalu tentukan titik kritis dengan benar.
- Tuliskan titik kritis pada sumbu bilangan dan bagi sumbu bilangan menjadi interval-interval yang berbeda.
- Pilih nilai uji dari setiap interval dan masukkan ke pertidaksamaan asli untuk menentukan tanda pertidaksamaan pada interval tersebut.
Tidak Memeriksa Tanda Pertidaksamaan
Setelah menentukan titik kritis dan membagi sumbu bilangan menjadi interval-interval, kamu perlu memeriksa tanda pertidaksamaan pada setiap interval. Tanda pertidaksamaan bisa berubah pada titik kritis.
Jika kamu tidak memeriksa tanda pertidaksamaan dengan benar, kamu bisa salah menentukan interval yang memenuhi pertidaksamaan.
Contoh Kesalahan, Contoh soal pertidaksamaan rasional
Misalnya, perhatikan pertidaksamaan berikut:
\[\fracx – 2x + 1 > 0\]
Jika kamu tidak memeriksa tanda pertidaksamaan dengan benar, kamu mungkin akan salah menentukan interval yang memenuhi pertidaksamaan. Misalnya, kamu mungkin akan menganggap bahwa interval (-∞, -1) memenuhi pertidaksamaan, padahal sebenarnya interval ini tidak memenuhi pertidaksamaan.
Cara Menghindari Kesalahan
- Selalu periksa tanda pertidaksamaan pada setiap interval.
- Pilih nilai uji dari setiap interval dan masukkan ke pertidaksamaan asli untuk menentukan tanda pertidaksamaan pada interval tersebut.
- Jika tanda pertidaksamaan sesuai dengan tanda yang diminta, maka interval tersebut memenuhi pertidaksamaan.
Tidak Memeriksa Penyebut
Penyebut pertidaksamaan tidak boleh sama dengan nol. Jika penyebut sama dengan nol, pertidaksamaan tidak terdefinisi.
Jika kamu tidak memeriksa penyebut dengan benar, kamu bisa salah menentukan interval yang memenuhi pertidaksamaan.
Contoh Kesalahan, Contoh soal pertidaksamaan rasional
Misalnya, perhatikan pertidaksamaan berikut:
\[\fracx – 2x + 1 > 0\]
Jika kamu tidak memeriksa penyebut dengan benar, kamu mungkin akan menganggap bahwa interval (-∞, -1) memenuhi pertidaksamaan, padahal sebenarnya interval ini tidak memenuhi pertidaksamaan karena penyebut sama dengan nol pada x = -1.
Cara Menghindari Kesalahan
- Selalu periksa penyebut pertidaksamaan.
- Tentukan nilai-nilai yang membuat penyebut sama dengan nol.
- Singkirkan nilai-nilai tersebut dari solusi pertidaksamaan.
Tidak Memeriksa Solusi
Setelah menentukan interval yang memenuhi pertidaksamaan, kamu perlu memeriksa solusi tersebut. Solusi pertidaksamaan harus memenuhi pertidaksamaan asli.
Jika kamu tidak memeriksa solusi dengan benar, kamu bisa salah menentukan solusi pertidaksamaan.
Contoh soal pertidaksamaan rasional bisa jadi rumit, tapi kalau dikaitkan dengan konsep kecepatan, jadi lebih seru! Bayangkan, kamu diminta menentukan batas kecepatan mobil yang aman berdasarkan jarak dan waktu tempuh. Nah, contoh soal kecepatan kelas 5 SD seperti yang ada di https://newcomerscuerna.org/contoh-soal-kecepatan-kelas-5-sd/ bisa membantu kamu memahami dasar-dasar kecepatan.
Dengan memahami konsep kecepatan, kamu akan lebih mudah memahami pertidaksamaan rasional yang melibatkan kecepatan, seperti menentukan batas kecepatan maksimum agar bisa sampai tujuan tepat waktu.
Contoh Kesalahan, Contoh soal pertidaksamaan rasional
Misalnya, perhatikan pertidaksamaan berikut:
\[\fracx – 2x + 1 > 0\]
Jika kamu tidak memeriksa solusi dengan benar, kamu mungkin akan menganggap bahwa x = 3 adalah solusi pertidaksamaan, padahal sebenarnya x = 3 tidak memenuhi pertidaksamaan.
Cara Menghindari Kesalahan
- Selalu periksa solusi pertidaksamaan.
- Masukkan solusi ke pertidaksamaan asli untuk memastikan bahwa solusi tersebut memenuhi pertidaksamaan.
Tips dan Trik
Memecahkan pertidaksamaan rasional bisa jadi menantang, tapi dengan strategi yang tepat, kamu bisa menguasainya! Berikut beberapa tips dan trik untuk membantumu dalam menyelesaikan pertidaksamaan rasional dengan lebih mudah.
Memilih Metode yang Tepat
Salah satu kunci untuk menyelesaikan pertidaksamaan rasional adalah memilih metode yang tepat. Ada dua metode utama yang bisa kamu gunakan:
- Metode Grafik: Metode ini sangat membantu untuk memahami secara visual solusi dari pertidaksamaan. Kamu bisa menggambar grafik fungsi rasional dan kemudian menentukan daerah mana yang memenuhi pertidaksamaan.
- Metode Aljabar: Metode ini melibatkan manipulasi aljabar untuk mencari solusi dari pertidaksamaan. Metode ini bisa lebih efektif untuk menyelesaikan pertidaksamaan yang lebih kompleks.
Untuk memilih metode yang tepat, perhatikan jenis pertidaksamaan yang kamu hadapi. Jika pertidaksamaan sederhana, metode grafik bisa menjadi pilihan yang lebih mudah. Namun, jika pertidaksamaan kompleks, metode aljabar mungkin lebih efisien.
Strategi Pemeriksaan Kembali
Setelah kamu menemukan solusi dari pertidaksamaan rasional, sangat penting untuk memeriksa kembali hasilnya. Berikut beberapa cara untuk memeriksa kembali solusi:
- Substitusi Nilai: Pilih beberapa nilai dari interval yang kamu temukan sebagai solusi dan substitusikan nilai tersebut ke dalam pertidaksamaan asli. Jika nilai tersebut memenuhi pertidaksamaan, maka interval tersebut merupakan bagian dari solusi.
- Titik Uji: Pilih titik uji di setiap interval yang kamu temukan. Substitusikan titik uji tersebut ke dalam pertidaksamaan asli dan perhatikan tanda hasil yang didapat. Jika tanda hasil sesuai dengan tanda pertidaksamaan, maka interval tersebut merupakan bagian dari solusi.
Dengan memeriksa kembali hasil, kamu bisa memastikan bahwa solusi yang kamu temukan benar dan tidak ada kesalahan.
Trik Praktis
Berikut beberapa trik praktis yang bisa membantumu dalam menyelesaikan pertidaksamaan rasional:
- Faktorkan Ekspresi: Jika memungkinkan, faktorkan ekspresi di pembilang dan penyebut pertidaksamaan. Ini bisa membantu kamu dalam menentukan titik-titik kritis dan interval solusi.
- Buat Tabel Tanda: Tabel tanda bisa membantu kamu dalam menentukan tanda hasil pertidaksamaan pada setiap interval. Tabel tanda berisi titik-titik kritis dan tanda hasil pertidaksamaan pada setiap interval.
- Perhatikan Titik-titik Kritis: Titik-titik kritis adalah nilai-nilai yang membuat pembilang atau penyebut pertidaksamaan sama dengan nol. Titik-titik kritis penting karena mereka membagi garis bilangan menjadi beberapa interval.
Dengan menerapkan tips dan trik ini, kamu akan lebih mudah dalam menyelesaikan pertidaksamaan rasional.
Latihan Soal
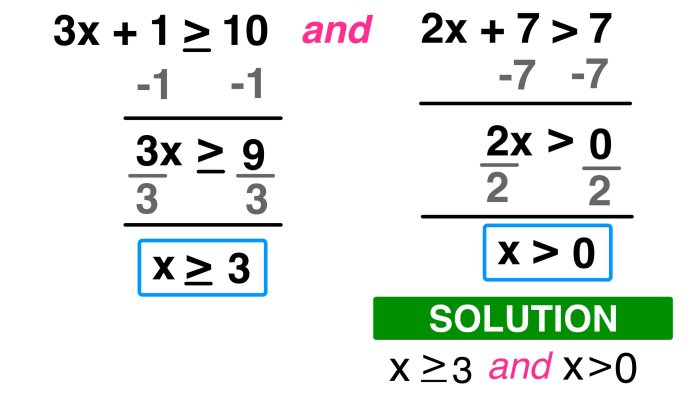
Setelah mempelajari materi tentang pertidaksamaan rasional, mari kita uji pemahaman Anda dengan beberapa latihan soal. Soal-soal berikut ini dirancang untuk mengasah kemampuan Anda dalam menyelesaikan pertidaksamaan rasional, baik yang sederhana maupun yang lebih kompleks.
Latihan Soal Pertidaksamaan Rasional
Berikut adalah 10 latihan soal pertidaksamaan rasional yang dapat Anda kerjakan. Soal-soal ini melibatkan berbagai jenis pertidaksamaan, mulai dari yang sederhana hingga yang lebih kompleks, sehingga Anda dapat menguji kemampuan Anda dalam menyelesaikan pertidaksamaan rasional secara menyeluruh.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx-2x+1 > 0$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\frac2x+1x-3 \le 1$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx^2-4x+2 < 0$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx^2+3x+2x-1 \ge 0$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx+1x^2-4 > 0$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\frac2x-1x^2+x-2 \le 0$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx^2-9x^2-4 < 0$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx^2+2x+1x^2-1 \ge 0$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx^3-8x^2-4 > 0$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx^4-1x^2+1 \le 0$.
Kunci Jawaban
Berikut adalah kunci jawaban dari latihan soal pertidaksamaan rasional yang telah diberikan sebelumnya. Gunakan kunci jawaban ini untuk mengecek hasil pekerjaan Anda dan memahami langkah-langkah penyelesaiannya.
- Himpunan penyelesaian dari pertidaksamaan $\fracx-2x+1 > 0$ adalah $x \in (-1, 2)$.
- Himpunan penyelesaian dari pertidaksamaan $\frac2x+1x-3 \le 1$ adalah $x \in (-\infty, 3) \cup [4, \infty)$.
- Himpunan penyelesaian dari pertidaksamaan $\fracx^2-4x+2 < 0$ adalah $x \in (-2, 2)$.
- Himpunan penyelesaian dari pertidaksamaan $\fracx^2+3x+2x-1 \ge 0$ adalah $x \in (-\infty, -2] \cup (-1, 1) \cup [1, \infty)$.
- Himpunan penyelesaian dari pertidaksamaan $\fracx+1x^2-4 > 0$ adalah $x \in (-2, -1) \cup (2, \infty)$.
- Himpunan penyelesaian dari pertidaksamaan $\frac2x-1x^2+x-2 \le 0$ adalah $x \in (-\infty, -2] \cup [\frac12, 1)$.
- Himpunan penyelesaian dari pertidaksamaan $\fracx^2-9x^2-4 < 0$ adalah $x \in (-2, 2) \cup (3, \infty)$.
- Himpunan penyelesaian dari pertidaksamaan $\fracx^2+2x+1x^2-1 \ge 0$ adalah $x \in (-\infty, -1] \cup (-1, 1) \cup [1, \infty)$.
- Himpunan penyelesaian dari pertidaksamaan $\fracx^3-8x^2-4 > 0$ adalah $x \in (-\infty, -2) \cup (2, \infty)$.
- Himpunan penyelesaian dari pertidaksamaan $\fracx^4-1x^2+1 \le 0$ adalah $x \in [-1, 1]$.
Soal Pertidaksamaan Rasional yang Menantang
Berikut adalah beberapa contoh soal pertidaksamaan rasional yang lebih menantang. Soal-soal ini dirancang untuk menguji kemampuan berpikir kritis Anda dalam menyelesaikan pertidaksamaan rasional.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx^2-4x+3x^2-5x+6 \ge 1$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx^3-x^2-2xx^2-4x+3 \le 0$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx^2+x-2x^3-x^2-2x > 1$.
- Tentukan himpunan penyelesaian dari pertidaksamaan $\fracx^4-16x^3-8 \le 0$.
Referensi
Untuk mempelajari lebih lanjut tentang pertidaksamaan rasional, Anda dapat merujuk pada berbagai sumber seperti buku teks matematika, artikel ilmiah, dan situs web edukasi. Berikut adalah beberapa referensi yang dapat Anda gunakan sebagai panduan.
Buku Teks Matematika
Buku teks matematika tingkat SMA atau perguruan tinggi yang membahas aljabar dan kalkulus biasanya mencakup topik pertidaksamaan rasional. Berikut beberapa contoh buku teks yang membahas topik ini:
- Aljabar oleh [Nama Pengarang] – Buku ini membahas konsep dasar aljabar, termasuk pertidaksamaan rasional, dengan contoh-contoh yang mudah dipahami.
- Kalkulus oleh [Nama Pengarang] – Buku ini membahas konsep kalkulus, termasuk turunan dan integral, yang dapat digunakan untuk menyelesaikan pertidaksamaan rasional.
Artikel Ilmiah
Artikel ilmiah yang membahas topik pertidaksamaan rasional dapat ditemukan di jurnal matematika atau situs web ilmiah. Artikel-artikel ini biasanya membahas aspek teoritis dan praktis dari pertidaksamaan rasional, serta aplikasi dalam berbagai bidang.
- “Solving Rational Inequalities” oleh [Nama Pengarang] – Artikel ini membahas metode penyelesaian pertidaksamaan rasional dengan menggunakan berbagai teknik aljabar dan kalkulus.
- “Applications of Rational Inequalities in Engineering” oleh [Nama Pengarang] – Artikel ini membahas aplikasi pertidaksamaan rasional dalam bidang teknik, seperti analisis struktur dan kontrol sistem.
Situs Web Edukasi
Situs web edukasi seperti Khan Academy dan Wolfram Alpha menyediakan sumber daya yang lengkap tentang pertidaksamaan rasional, termasuk video pembelajaran, latihan soal, dan penjelasan konsep.
- Khan Academy – Situs web ini menyediakan video pembelajaran dan latihan soal tentang pertidaksamaan rasional, yang dijelaskan dengan mudah dan interaktif.
- Wolfram Alpha – Situs web ini menyediakan kalkulator dan alat bantu untuk menyelesaikan pertidaksamaan rasional, serta penjelasan konsep dan contoh soal.
Rekomendasi Buku atau Website
Berikut adalah beberapa rekomendasi buku atau website yang membahas topik terkait dengan pertidaksamaan rasional:
- “Precalculus” oleh [Nama Pengarang] – Buku ini membahas topik precalculus, termasuk pertidaksamaan rasional, dengan contoh-contoh yang relevan dan latihan soal yang menantang.
- “Algebra and Trigonometry” oleh [Nama Pengarang] – Buku ini membahas topik aljabar dan trigonometri, termasuk pertidaksamaan rasional, dengan penjelasan yang jelas dan ringkas.
- MathWorld – Situs web ini menyediakan informasi yang komprehensif tentang matematika, termasuk pertidaksamaan rasional, dengan penjelasan yang mendalam dan contoh-contoh yang menarik.
Kesimpulan
Memahami pertidaksamaan rasional tidak hanya penting dalam konteks matematika semata, tetapi juga membuka jalan untuk memahami dan menyelesaikan masalah-masalah di berbagai bidang, seperti ekonomi, sains, dan bahkan kehidupan sehari-hari. Dengan menguasai konsep dan metode yang telah kita bahas, Anda akan memiliki bekal yang kuat untuk menghadapi berbagai tantangan yang melibatkan pertidaksamaan rasional.





