Contoh soal peubah acak kontinu – Peubah acak kontinu, seperti tinggi badan atau suhu, merupakan konsep penting dalam probabilitas dan statistika. Bayangkan Anda sedang meneliti tinggi badan siswa di suatu kelas. Tinggi badan setiap siswa dapat bervariasi, membentuk rentang nilai yang berkelanjutan. Bagaimana kita bisa menghitung peluang seorang siswa memiliki tinggi badan tertentu? Nah, di sini peubah acak kontinu berperan penting.
Dalam artikel ini, kita akan menjelajahi peubah acak kontinu dengan lebih dalam, mempelajari sifat-sifatnya, dan mengaplikasikannya dalam berbagai contoh soal. Mari kita selami dunia data yang berkelanjutan dan pahami bagaimana peluang bekerja di dalamnya.
Pengertian Peubah Acak Kontinu
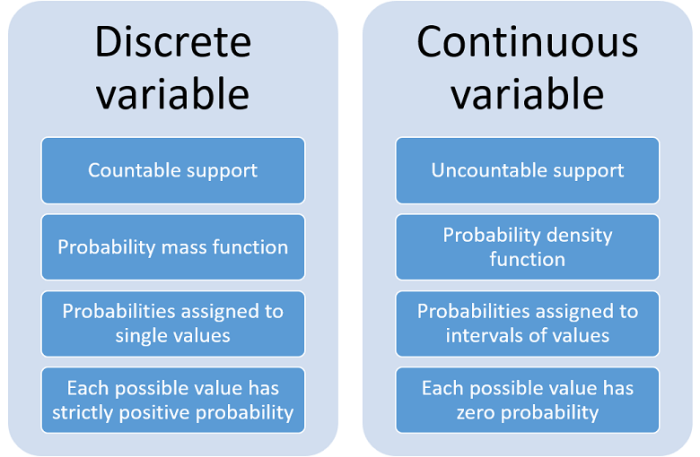
Dalam dunia statistika, peubah acak merupakan variabel yang nilainya ditentukan oleh hasil suatu kejadian acak. Peubah acak ini dibagi menjadi dua jenis, yaitu peubah acak diskrit dan peubah acak kontinu. Peubah acak kontinu adalah jenis peubah acak yang nilainya dapat mengambil nilai apa pun dalam rentang tertentu. Dalam arti lain, peubah acak kontinu dapat memiliki nilai yang tak terhitung jumlahnya dalam suatu interval tertentu. Untuk memahami lebih lanjut tentang peubah acak kontinu, mari kita bahas pengertiannya secara lebih detail.
Pengertian Peubah Acak Kontinu
Peubah acak kontinu adalah variabel yang nilainya dapat mengambil semua nilai dalam suatu interval tertentu. Dengan kata lain, nilai peubah acak kontinu tidak terbatas pada nilai-nilai tertentu saja, tetapi dapat mengambil nilai apa pun di antara dua nilai yang diberikan. Perbedaannya dengan peubah acak diskrit terletak pada kemampuannya untuk mengambil nilai yang tak terhitung jumlahnya.
Contoh Peubah Acak Kontinu dalam Kehidupan Sehari-hari
Peubah acak kontinu dapat ditemukan di berbagai aspek kehidupan sehari-hari. Berikut beberapa contohnya:
- Tinggi badan: Tinggi badan seseorang dapat mengambil nilai apa pun dalam rentang tertentu, misalnya antara 150 cm hingga 180 cm. Nilai tinggi badan dapat berupa 155 cm, 162,5 cm, 178,3 cm, dan seterusnya. Tidak ada batasan nilai yang dapat diambil oleh tinggi badan.
- Suhu ruangan: Suhu ruangan dapat mengambil nilai apa pun dalam rentang tertentu, misalnya antara 20 derajat Celcius hingga 30 derajat Celcius. Nilai suhu dapat berupa 22,5 derajat Celcius, 27,8 derajat Celcius, 29,1 derajat Celcius, dan seterusnya. Nilai suhu dapat mengambil nilai desimal, sehingga tidak terbatas pada nilai bulat saja.
- Berat badan: Berat badan seseorang dapat mengambil nilai apa pun dalam rentang tertentu, misalnya antara 50 kg hingga 80 kg. Nilai berat badan dapat berupa 55,3 kg, 62,7 kg, 78,1 kg, dan seterusnya. Tidak ada batasan nilai yang dapat diambil oleh berat badan.
Perbedaan Peubah Acak Kontinu dan Peubah Acak Diskrit
Peubah acak kontinu dan peubah acak diskrit memiliki perbedaan yang mendasar. Peubah acak diskrit hanya dapat mengambil nilai-nilai tertentu yang terhitung jumlahnya, sedangkan peubah acak kontinu dapat mengambil nilai apa pun dalam rentang tertentu. Berikut tabel yang merangkum perbedaan antara keduanya:
| Karakteristik | Peubah Acak Kontinu | Peubah Acak Diskrit |
|---|---|---|
| Nilai yang dapat diambil | Semua nilai dalam rentang tertentu | Nilai-nilai tertentu yang terhitung jumlahnya |
| Contoh | Tinggi badan, suhu ruangan, berat badan | Jumlah mobil yang lewat, jumlah kepala dalam pelemparan koin, jumlah siswa dalam kelas |
| Grafik | Kurva kontinu | Histogram atau bar chart |
Sifat Peubah Acak Kontinu
Dalam dunia probabilitas dan statistika, peubah acak merupakan konsep fundamental yang membantu kita memahami dan menganalisis peristiwa acak. Peubah acak kontinu, yang merupakan fokus pembahasan kita kali ini, memiliki karakteristik unik yang membedakannya dari peubah acak diskrit. Peubah acak kontinu dapat mengambil nilai di sepanjang rentang kontinu, tidak terbatas pada nilai-nilai diskrit tertentu. Mari kita jelajahi sifat-sifat yang mendefinisikan peubah acak kontinu dan bagaimana sifat-sifat ini memengaruhi analisis data.
Sifat Peubah Acak Kontinu
Peubah acak kontinu memiliki beberapa sifat penting yang membedakannya dari peubah acak diskrit. Berikut adalah beberapa sifat utama yang perlu dipahami:
- Nilai kontinu: Peubah acak kontinu dapat mengambil nilai apa pun dalam rentang tertentu, bukan hanya nilai diskrit. Misalnya, tinggi badan seseorang dapat mengambil nilai apa pun di antara 150 cm dan 180 cm, bukan hanya nilai-nilai tertentu seperti 150 cm, 151 cm, 152 cm, dan seterusnya.
- Probabilitas pada interval: Probabilitas peubah acak kontinu berada dalam interval tertentu, bukan pada satu nilai tunggal. Misalnya, probabilitas tinggi badan seseorang berada antara 160 cm dan 170 cm dapat dihitung, tetapi probabilitas tinggi badan seseorang persis 165 cm adalah nol.
- Fungsi kepadatan probabilitas: Peubah acak kontinu didefinisikan oleh fungsi kepadatan probabilitas (PDF), yang menunjukkan probabilitas relatif dari peubah acak mengambil nilai tertentu dalam rentang tertentu. Luas di bawah kurva PDF pada interval tertentu memberikan probabilitas peubah acak berada dalam interval tersebut.
Karakteristik Distribusi Probabilitas Peubah Acak Kontinu, Contoh soal peubah acak kontinu
Distribusi probabilitas peubah acak kontinu memiliki karakteristik yang unik yang memengaruhi analisis data. Berikut adalah beberapa karakteristik utama:
- Bentuk: Distribusi probabilitas peubah acak kontinu dapat memiliki berbagai bentuk, seperti bentuk lonceng, bentuk miring, atau bentuk uniform. Bentuk distribusi menentukan bagaimana probabilitas tersebar di sepanjang rentang nilai peubah acak.
- Rata-rata (Mean): Rata-rata atau mean dari distribusi probabilitas menunjukkan nilai pusat distribusi. Ini adalah nilai yang diharapkan dari peubah acak.
- Simpangan baku (Standard Deviation): Simpangan baku mengukur sebaran data di sekitar mean. Simpangan baku yang tinggi menunjukkan bahwa data tersebar lebih luas, sedangkan simpangan baku yang rendah menunjukkan bahwa data lebih terpusat di sekitar mean.
Contoh Penerapan Sifat Peubah Acak Kontinu
Sifat-sifat peubah acak kontinu memiliki aplikasi yang luas dalam berbagai bidang, seperti statistika, ilmu data, dan rekayasa. Berikut adalah contoh bagaimana sifat-sifat tersebut memengaruhi analisis data:
- Analisis pertumbuhan tanaman: Tinggi tanaman merupakan peubah acak kontinu. Kita dapat menggunakan fungsi kepadatan probabilitas untuk memodelkan pertumbuhan tanaman dan memprediksi tinggi rata-rata tanaman di suatu populasi. Kita juga dapat menggunakan simpangan baku untuk mengukur variasi tinggi tanaman di sekitar rata-rata.
- Analisis suhu: Suhu merupakan peubah acak kontinu. Kita dapat menggunakan distribusi probabilitas untuk memodelkan suhu harian di suatu lokasi dan memprediksi suhu rata-rata, suhu maksimum, dan suhu minimum. Kita juga dapat menggunakan simpangan baku untuk mengukur variasi suhu di sekitar rata-rata.
Jenis-Jenis Distribusi Peubah Acak Kontinu
Dalam analisis statistik, peubah acak kontinu digunakan untuk menggambarkan variabel yang dapat mengambil nilai apa pun dalam rentang tertentu. Untuk memahami dan memodelkan peubah acak kontinu, kita memerlukan distribusi probabilitas yang sesuai. Distribusi probabilitas ini memberikan kita gambaran tentang kemungkinan suatu peubah acak kontinu mengambil nilai tertentu.
Ada berbagai jenis distribusi probabilitas yang umum digunakan untuk peubah acak kontinu. Setiap distribusi memiliki karakteristik unik dan cocok untuk memodelkan berbagai jenis fenomena. Berikut ini adalah beberapa jenis distribusi probabilitas yang umum digunakan untuk peubah acak kontinu:
Distribusi Normal
Distribusi normal, juga dikenal sebagai distribusi Gaussian, adalah salah satu distribusi probabilitas yang paling penting dan umum digunakan dalam statistik. Distribusi ini berbentuk lonceng simetris, dengan puncaknya di tengah. Distribusi normal dicirikan oleh dua parameter: mean (μ) dan standar deviasi (σ). Mean menunjukkan lokasi pusat distribusi, sedangkan standar deviasi menunjukkan penyebaran data.
Contoh soal peubah acak kontinu bisa dijumpai dalam berbagai materi matematika, termasuk soal-soal tes masuk perguruan tinggi. Namun, jangan salah, konsep ini juga penting untuk dipelajari bagi kamu yang ingin bekerja di bidang perbankan, lho! Misalnya, di contoh soal tes Bank Jateng , kamu mungkin akan menemukan soal yang berkaitan dengan peluang atau probabilitas, yang merupakan dasar dari peubah acak kontinu.
Jadi, jangan menganggap remeh materi ini, ya!
Distribusi normal memiliki banyak aplikasi dalam berbagai bidang, seperti:
- Ilmu Pengetahuan Alam: Memmodelkan tinggi badan, berat badan, tekanan darah, dan banyak variabel biologis lainnya.
- Teknik: Memmodelkan kesalahan pengukuran, variasi dalam proses manufaktur, dan keausan komponen.
- Finansial: Memmodelkan pengembalian saham, harga aset, dan risiko investasi.
Distribusi Eksponensial
Distribusi eksponensial digunakan untuk memodelkan waktu antara kejadian yang terjadi secara independen dalam proses Poisson. Distribusi ini memiliki ekor kanan yang panjang, yang menunjukkan bahwa ada kemungkinan kecil untuk memiliki waktu yang sangat lama antara kejadian.
Distribusi eksponensial memiliki aplikasi dalam berbagai bidang, seperti:
- Keandalan: Memmodelkan umur komponen elektronik, mesin, dan sistem lainnya.
- Antrian: Memmodelkan waktu tunggu pelanggan di antrian.
- Radioaktif: Memmodelkan waktu peluruhan radioaktif.
Distribusi Uniform
Distribusi uniform digunakan untuk memodelkan variabel yang memiliki kemungkinan sama untuk mengambil nilai apa pun dalam rentang tertentu. Distribusi ini memiliki bentuk persegi panjang, dengan semua nilai memiliki probabilitas yang sama.
Distribusi uniform memiliki aplikasi dalam berbagai bidang, seperti:
- Pembangkitan Bilangan Acak: Membangkitkan bilangan acak yang terdistribusi secara uniform.
- Simulasi: Memmodelkan variabel acak yang memiliki probabilitas yang sama untuk mengambil nilai apa pun dalam rentang tertentu.
- Statistik Deskriptif: Menghitung rata-rata dan standar deviasi dari data yang terdistribusi secara uniform.
Distribusi Gamma
Distribusi gamma adalah distribusi probabilitas yang umum digunakan untuk memodelkan variabel yang mengambil nilai positif. Distribusi ini memiliki dua parameter: parameter bentuk (α) dan parameter skala (β). Parameter bentuk menentukan bentuk distribusi, sedangkan parameter skala menentukan skala distribusi.
Distribusi gamma memiliki aplikasi dalam berbagai bidang, seperti:
- Keandalan: Memmodelkan umur komponen elektronik, mesin, dan sistem lainnya.
- Hidrologi: Memmodelkan curah hujan, aliran sungai, dan tinggi muka air.
- Statistik Medis: Memmodelkan waktu tunggu sampai kejadian, seperti waktu tunggu sampai pasien sembuh dari penyakit.
Distribusi Beta
Distribusi beta digunakan untuk memodelkan variabel yang mengambil nilai antara 0 dan 1. Distribusi ini memiliki dua parameter: parameter bentuk pertama (α) dan parameter bentuk kedua (β). Parameter bentuk menentukan bentuk distribusi, dengan nilai α dan β yang lebih besar menghasilkan distribusi yang lebih terkonsentrasi di tengah.
Distribusi beta memiliki aplikasi dalam berbagai bidang, seperti:
- Probabilitas: Memmodelkan probabilitas keberhasilan suatu peristiwa.
- Statistik Bayesian: Memmodelkan distribusi prior untuk parameter model.
- Pemrosesan Citra: Memmodelkan intensitas piksel dalam gambar.
Memilih Distribusi yang Tepat
Memilih distribusi yang tepat untuk menganalisis data peubah acak kontinu tergantung pada sifat data dan tujuan analisis. Berikut adalah beberapa faktor yang perlu dipertimbangkan:
- Bentuk Distribusi: Apakah data memiliki bentuk lonceng simetris (normal), ekor kanan yang panjang (eksponensial), atau bentuk persegi panjang (uniform)?
- Rentang Data: Apakah data mengambil nilai positif (gamma), antara 0 dan 1 (beta), atau rentang lainnya?
- Tujuan Analisis: Apakah tujuannya untuk memodelkan waktu tunggu (eksponensial), probabilitas keberhasilan (beta), atau variabel lain?
Selain itu, kita dapat menggunakan metode statistik seperti uji goodness-of-fit untuk menentukan distribusi yang paling cocok untuk data kita.
Menentukan Probabilitas Peubah Acak Kontinu
Dalam teori probabilitas, peubah acak kontinu merupakan peubah yang dapat mengambil nilai apa pun dalam rentang tertentu. Untuk memahami perilaku peubah acak kontinu, kita perlu mengetahui probabilitasnya untuk berada dalam rentang nilai tertentu. Artikel ini akan membahas cara menentukan probabilitas peubah acak kontinu dengan menggunakan fungsi distribusi kumulatif (CDF) dan fungsi kepadatan probabilitas (PDF).
Menentukan Probabilitas dengan Fungsi Distribusi Kumulatif (CDF)
Fungsi distribusi kumulatif (CDF) dari peubah acak kontinu X, yang dinotasikan sebagai F(x), memberikan probabilitas bahwa X akan mengambil nilai kurang dari atau sama dengan x. Dengan kata lain, F(x) = P(X ≤ x). CDF adalah fungsi monoton naik yang nilainya berada antara 0 dan 1. Berikut adalah beberapa sifat penting dari CDF:
- F(-∞) = 0: Probabilitas bahwa X lebih kecil dari minus tak hingga adalah 0.
- F(∞) = 1: Probabilitas bahwa X lebih kecil dari tak hingga adalah 1.
- F(x) adalah fungsi monoton naik: Jika x1 < x2, maka F(x1) ≤ F(x2).
Untuk menentukan probabilitas bahwa X berada dalam rentang nilai tertentu, misalkan a ≤ X ≤ b, kita dapat menggunakan CDF sebagai berikut:
P(a ≤ X ≤ b) = F(b) – F(a)
Rumus ini menyatakan bahwa probabilitas X berada di antara a dan b sama dengan selisih antara nilai CDF di b dan nilai CDF di a.
Menentukan Probabilitas dengan Fungsi Kepadatan Probabilitas (PDF)
Fungsi kepadatan probabilitas (PDF) dari peubah acak kontinu X, yang dinotasikan sebagai f(x), memberikan probabilitas bahwa X akan mengambil nilai dalam interval kecil di sekitar x. PDF adalah fungsi non-negatif yang luas di bawah kurva sama dengan 1. Berikut adalah beberapa sifat penting dari PDF:
- f(x) ≥ 0 untuk semua x.
- ∫f(x)dx = 1, di mana integrasi dilakukan pada seluruh rentang nilai X.
Untuk menentukan probabilitas bahwa X berada dalam rentang nilai tertentu, misalkan a ≤ X ≤ b, kita dapat menggunakan PDF sebagai berikut:
P(a ≤ X ≤ b) = ∫ab f(x)dx
Rumus ini menyatakan bahwa probabilitas X berada di antara a dan b sama dengan integral dari PDF di antara a dan b.
Contoh Soal
Misalkan X adalah peubah acak kontinu yang menyatakan tinggi badan seorang mahasiswa di suatu universitas, dengan PDF sebagai berikut:
f(x) =
0.01(x – 150) jika 150 ≤ x ≤ 170
0.01(180 – x) jika 170 ≤ x ≤ 180
0 lainnya
Tentukan probabilitas bahwa tinggi badan seorang mahasiswa di universitas tersebut berada di antara 160 cm dan 175 cm.
Untuk menentukan probabilitas tersebut, kita dapat menggunakan rumus:
P(160 ≤ X ≤ 175) = ∫160175 f(x)dx
Karena 160 dan 175 berada dalam rentang 150 ≤ x ≤ 170, kita dapat menggunakan bagian pertama dari fungsi PDF:
P(160 ≤ X ≤ 175) = ∫160175 0.01(x – 150)dx
Menghitung integral tersebut, kita dapatkan:
P(160 ≤ X ≤ 175) = [0.005(x – 150)2]160175 = 0.625
Jadi, probabilitas bahwa tinggi badan seorang mahasiswa di universitas tersebut berada di antara 160 cm dan 175 cm adalah 0.625 atau 62.5%.
Menentukan Nilai Harapan dan Variansi
Setelah kita memahami konsep peubah acak kontinu, langkah selanjutnya adalah menentukan nilai harapan dan variansi dari peubah tersebut. Nilai harapan, juga dikenal sebagai rata-rata, memberikan kita gambaran tentang nilai tengah dari distribusi peubah acak. Sementara variansi mengukur seberapa tersebar data dari nilai tengahnya. Dalam konteks peubah acak kontinu, perhitungan ini melibatkan integral dan fungsi kepadatan probabilitas.
Cara Menentukan Nilai Harapan dan Variansi
Untuk menentukan nilai harapan dan variansi dari peubah acak kontinu, kita memerlukan fungsi kepadatan probabilitas (f(x)) yang menggambarkan distribusi peubah tersebut. Berikut langkah-langkahnya:
- Nilai Harapan (E(X)): Nilai harapan dari peubah acak kontinu X dihitung dengan mengintegralkan hasil kali antara nilai x dan fungsi kepadatan probabilitasnya (f(x)) di seluruh domain x. Rumusnya adalah:
E(X) = ∫-∞∞ x * f(x) dx
- Variansi (Var(X)): Variansi dari peubah acak kontinu X dihitung dengan mengintegralkan hasil kali antara kuadrat selisih antara nilai x dan nilai harapannya (E(X)) dengan fungsi kepadatan probabilitasnya (f(x)) di seluruh domain x. Rumusnya adalah:
Var(X) = ∫-∞∞ (x – E(X))2 * f(x) dx
Contoh Soal
Misalkan kita memiliki peubah acak kontinu X yang menyatakan waktu tunggu (dalam menit) di sebuah antrian. Fungsi kepadatan probabilitasnya adalah:
f(x) = 1/10, 0 ≤ x ≤ 10
0, x 10
Kita ingin menentukan nilai harapan dan variansi waktu tunggu di antrian ini.
- Nilai Harapan (E(X)):
E(X) = ∫010 x * (1/10) dx = (1/10) * [x2/2]010 = 5 menit
- Variansi (Var(X)):
Var(X) = ∫010 (x – 5)2 * (1/10) dx = (1/10) * [(x – 5)3/3]010 = 8.33 menit2
Jadi, nilai harapan waktu tunggu di antrian adalah 5 menit, dan variansinya adalah 8.33 menit2.
Tabel Rumus dan Contoh Perhitungan
| Distribusi | Fungsi Kepadatan Probabilitas (f(x)) | Nilai Harapan (E(X)) | Variansi (Var(X)) |
|---|---|---|---|
| Eksponensial | f(x) = λe-λx, x ≥ 0 | E(X) = 1/λ | Var(X) = 1/λ2 |
| Normal | f(x) = (1/σ√(2π)) * e-((x-μ)2/(2σ2)) | E(X) = μ | Var(X) = σ2 |
| Uniform | f(x) = 1/(b-a), a ≤ x ≤ b | E(X) = (a + b)/2 | Var(X) = (b-a)2/12 |
Tabel di atas menunjukkan rumus dan contoh perhitungan nilai harapan dan variansi untuk beberapa distribusi peubah acak kontinu yang umum digunakan.
Aplikasi Peubah Acak Kontinu dalam Kehidupan Nyata
Peubah acak kontinu, yang nilainya dapat mengambil setiap nilai dalam rentang tertentu, memainkan peran penting dalam berbagai bidang kehidupan nyata. Peubah acak kontinu membantu kita memahami dan memodelkan fenomena alam dan sosial yang bervariasi secara kontinu, seperti tinggi badan, suhu, tekanan darah, dan harga saham. Dengan memahami perilaku peubah acak kontinu, kita dapat memperoleh wawasan yang berharga untuk pengambilan keputusan yang lebih baik.
Aplikasi Peubah Acak Kontinu dalam Berbagai Bidang
Peubah acak kontinu memiliki aplikasi yang luas dalam berbagai bidang, termasuk:
- Ekonomi: Peubah acak kontinu digunakan untuk memodelkan fluktuasi harga saham, suku bunga, dan tingkat inflasi. Model-model statistik yang melibatkan peubah acak kontinu membantu investor dan ekonom dalam memahami risiko dan peluang dalam pasar keuangan.
- Ilmu Komputer: Dalam ilmu komputer, peubah acak kontinu digunakan dalam pemodelan jaringan komputer, analisis kinerja sistem, dan pengembangan algoritma pembelajaran mesin. Misalnya, dalam pemodelan jaringan komputer, peubah acak kontinu dapat digunakan untuk memodelkan waktu tunggu paket data atau waktu respon server.
- Kesehatan: Peubah acak kontinu digunakan untuk memodelkan variabel fisiologis seperti tekanan darah, denyut jantung, dan kadar gula darah. Dalam penelitian klinis, peubah acak kontinu membantu para peneliti dalam memahami efektivitas pengobatan dan risiko kesehatan.
Memmodelkan Fenomena Alam dan Sosial
Peubah acak kontinu memberikan alat yang kuat untuk memodelkan fenomena alam dan sosial. Misalnya, dalam meteorologi, peubah acak kontinu digunakan untuk memodelkan suhu, curah hujan, dan kecepatan angin. Model-model statistik yang melibatkan peubah acak kontinu membantu para ahli meteorologi dalam memprediksi cuaca dan memberikan peringatan dini tentang peristiwa cuaca ekstrem.
- Suhu: Suhu udara merupakan contoh peubah acak kontinu yang bervariasi secara kontinu dalam rentang tertentu. Model statistik dapat digunakan untuk memprediksi suhu harian, mingguan, atau bulanan berdasarkan data historis dan faktor-faktor lainnya.
- Tinggi Badan: Tinggi badan manusia merupakan contoh peubah acak kontinu yang bervariasi secara kontinu dalam rentang tertentu. Model statistik dapat digunakan untuk memahami distribusi tinggi badan dalam populasi tertentu, dan untuk memprediksi tinggi badan anak-anak berdasarkan data genetik dan lingkungan.
Analisis Data Peubah Acak Kontinu dalam Pengambilan Keputusan
Analisis data peubah acak kontinu dapat memberikan wawasan yang berharga untuk pengambilan keputusan. Misalnya, dalam bisnis, peubah acak kontinu dapat digunakan untuk memodelkan permintaan produk, biaya produksi, dan pendapatan. Dengan menganalisis data ini, perusahaan dapat membuat keputusan yang lebih tepat mengenai strategi pemasaran, penetapan harga, dan manajemen persediaan.
- Permintaan Produk: Permintaan produk merupakan contoh peubah acak kontinu yang bervariasi secara kontinu dalam rentang tertentu. Model statistik dapat digunakan untuk memprediksi permintaan produk berdasarkan faktor-faktor seperti tren pasar, musim, dan promosi.
- Biaya Produksi: Biaya produksi merupakan contoh peubah acak kontinu yang bervariasi secara kontinu dalam rentang tertentu. Model statistik dapat digunakan untuk memprediksi biaya produksi berdasarkan faktor-faktor seperti harga bahan baku, biaya tenaga kerja, dan biaya overhead.
Contoh Soal Peubah Acak Kontinu
Peubah acak kontinu adalah peubah yang nilainya dapat mengambil nilai apa pun dalam suatu rentang tertentu. Contohnya adalah tinggi badan, berat badan, suhu, dan waktu. Dalam matematika, peubah acak kontinu didefinisikan sebagai peubah yang fungsi distribusi kumulatifnya (CDF) kontinu. Artinya, CDF-nya dapat digambar sebagai kurva yang halus tanpa lompatan atau titik diskontinu. Artikel ini akan membahas beberapa contoh soal peubah acak kontinu dan menjelaskan langkah-langkah penyelesaiannya.
Contoh Soal 1: Distribusi Eksponensial
Sebuah perusahaan telepon memiliki rata-rata 5 panggilan per jam. Asumsikan bahwa waktu antar panggilan mengikuti distribusi eksponensial. Tentukan probabilitas bahwa waktu antar panggilan berikutnya lebih dari 10 menit.
- Langkah 1: Tentukan parameter distribusi eksponensial. Dalam kasus ini, rata-rata waktu antar panggilan adalah 5 panggilan per jam, yang berarti bahwa rata-rata waktu antar panggilan adalah 1/5 jam atau 12 menit.
- Langkah 2: Gunakan rumus distribusi eksponensial untuk menghitung probabilitas. Probabilitas bahwa waktu antar panggilan berikutnya lebih dari 10 menit adalah:
P(X > 10) = e^(-10/12) = 0.472
Oleh karena itu, probabilitas bahwa waktu antar panggilan berikutnya lebih dari 10 menit adalah 0.472 atau 47.2%.
Ilustrasi: Diagram distribusi eksponensial dengan garis vertikal yang menunjukkan waktu 10 menit dan area di bawah kurva yang menunjukkan probabilitas waktu antar panggilan lebih dari 10 menit.
Contoh Soal 2: Distribusi Normal
Tinggi badan pria dewasa di suatu negara berdistribusi normal dengan rata-rata 175 cm dan standar deviasi 5 cm. Tentukan probabilitas bahwa tinggi badan pria dewasa secara acak yang dipilih lebih dari 180 cm.
- Langkah 1: Standarkan peubah acak. Dalam kasus ini, kita perlu menstandarkan tinggi badan 180 cm menjadi skor-z. Skor-z adalah jarak antara nilai yang diberikan dan rata-rata, dibagi dengan standar deviasi. Skor-z untuk tinggi badan 180 cm adalah:
z = (180 – 175) / 5 = 1
- Langkah 2: Gunakan tabel distribusi normal standar untuk menghitung probabilitas. Probabilitas bahwa tinggi badan pria dewasa secara acak yang dipilih lebih dari 180 cm sama dengan probabilitas bahwa skor-z lebih dari 1. Dari tabel distribusi normal standar, kita tahu bahwa probabilitas ini adalah 0.1587.
Oleh karena itu, probabilitas bahwa tinggi badan pria dewasa secara acak yang dipilih lebih dari 180 cm adalah 0.1587 atau 15.87%.
Ilustrasi: Diagram distribusi normal dengan garis vertikal yang menunjukkan tinggi badan 180 cm dan area di bawah kurva yang menunjukkan probabilitas tinggi badan lebih dari 180 cm.
Contoh Soal 3: Distribusi Seragam
Sebuah mesin menghasilkan angka acak antara 0 dan 1 secara seragam. Tentukan probabilitas bahwa angka yang dihasilkan lebih besar dari 0.5.
- Langkah 1: Tentukan rentang nilai peubah acak. Dalam kasus ini, rentang nilai peubah acak adalah dari 0 hingga 1.
- Langkah 2: Gunakan rumus distribusi seragam untuk menghitung probabilitas. Probabilitas bahwa angka yang dihasilkan lebih besar dari 0.5 adalah:
P(X > 0.5) = (1 – 0.5) / (1 – 0) = 0.5
Oleh karena itu, probabilitas bahwa angka yang dihasilkan lebih besar dari 0.5 adalah 0.5 atau 50%.
Ilustrasi: Diagram distribusi seragam dengan garis vertikal yang menunjukkan angka 0.5 dan area di bawah kurva yang menunjukkan probabilitas angka lebih besar dari 0.5.
Contoh Soal 4: Distribusi Gamma
Sebuah perusahaan asuransi mencatat bahwa rata-rata jumlah klaim yang diajukan per hari adalah 10. Asumsikan bahwa jumlah klaim mengikuti distribusi gamma dengan parameter α = 10 dan β = 1. Tentukan probabilitas bahwa jumlah klaim pada hari tertentu lebih dari 15.
- Langkah 1: Gunakan rumus distribusi gamma untuk menghitung probabilitas. Probabilitas bahwa jumlah klaim pada hari tertentu lebih dari 15 adalah:
P(X > 15) = ∫15∞ (1/Γ(10)) * x9 * e-x dx
di mana Γ(10) adalah fungsi gamma dari 10. Integral ini tidak dapat dihitung secara analitis, tetapi dapat dihitung menggunakan perangkat lunak statistik.
Ilustrasi: Diagram distribusi gamma dengan garis vertikal yang menunjukkan jumlah klaim 15 dan area di bawah kurva yang menunjukkan probabilitas jumlah klaim lebih dari 15.
Contoh Soal 5: Distribusi Beta
Sebuah perusahaan memproduksi baterai yang memiliki masa pakai rata-rata 100 jam. Asumsikan bahwa masa pakai baterai mengikuti distribusi beta dengan parameter α = 2 dan β = 3. Tentukan probabilitas bahwa masa pakai baterai secara acak yang dipilih lebih dari 120 jam.
- Langkah 1: Gunakan rumus distribusi beta untuk menghitung probabilitas. Probabilitas bahwa masa pakai baterai secara acak yang dipilih lebih dari 120 jam adalah:
P(X > 120) = ∫120100 (1/B(2, 3)) * x1 * (1 – x)2 dx
di mana B(2, 3) adalah fungsi beta dari 2 dan 3. Integral ini tidak dapat dihitung secara analitis, tetapi dapat dihitung menggunakan perangkat lunak statistik.
Ilustrasi: Diagram distribusi beta dengan garis vertikal yang menunjukkan masa pakai baterai 120 jam dan area di bawah kurva yang menunjukkan probabilitas masa pakai baterai lebih dari 120 jam.
Peubah Acak Kontinu dalam Statistik Inferensial
Peubah acak kontinu merupakan salah satu konsep fundamental dalam statistik inferensial. Peubah ini berperan penting dalam membantu kita menarik kesimpulan tentang populasi berdasarkan data sampel. Peubah acak kontinu dapat mengambil nilai apa pun dalam rentang tertentu, dan seringkali digunakan untuk memodelkan variabel-variabel seperti tinggi badan, berat badan, suhu, dan waktu.
Penggunaan Peubah Acak Kontinu dalam Statistik Inferensial
Dalam statistik inferensial, peubah acak kontinu digunakan untuk membuat estimasi parameter populasi dan menguji hipotesis tentang populasi. Estimasi parameter adalah proses menentukan nilai terbaik untuk parameter populasi berdasarkan data sampel. Pengujian hipotesis adalah proses menentukan apakah ada bukti yang cukup untuk menolak hipotesis nol tentang populasi.
Contoh Penggunaan Peubah Acak Kontinu
Misalnya, kita ingin mengetahui tinggi badan rata-rata mahasiswa di sebuah universitas. Kita dapat mengambil sampel mahasiswa dan mengukur tinggi badan mereka. Tinggi badan adalah peubah acak kontinu, karena dapat mengambil nilai apa pun dalam rentang tertentu. Kita dapat menggunakan data sampel ini untuk membuat estimasi tinggi badan rata-rata mahasiswa di seluruh universitas. Kita juga dapat menggunakan data sampel ini untuk menguji hipotesis bahwa tinggi badan rata-rata mahasiswa di universitas ini sama dengan tinggi badan rata-rata mahasiswa di universitas lain.
Metode Statistik untuk Analisis Data Peubah Acak Kontinu
Ada beberapa metode statistik yang digunakan untuk menganalisis data peubah acak kontinu dalam konteks inferensial, di antaranya:
- Uji-t: Uji-t digunakan untuk membandingkan rata-rata dua kelompok data, atau untuk membandingkan rata-rata sampel dengan nilai populasi yang diketahui.
- Uji-z: Uji-z digunakan untuk membandingkan rata-rata dua kelompok data yang besar, atau untuk membandingkan rata-rata sampel dengan nilai populasi yang diketahui, ketika standar deviasi populasi diketahui.
- Analisis Varian (ANOVA): ANOVA digunakan untuk membandingkan rata-rata lebih dari dua kelompok data.
- Regresi Linier: Regresi linier digunakan untuk mempelajari hubungan antara dua variabel kontinu.
Peran Software Statistik dalam Analisis Peubah Acak Kontinu
Dalam analisis data, pemahaman tentang peubah acak kontinu sangat penting. Peubah acak kontinu adalah variabel yang dapat mengambil nilai apa pun dalam rentang tertentu. Software statistik seperti R atau Python memberikan alat yang kuat untuk menganalisis data peubah acak kontinu dengan mudah dan efisien. Software ini menyediakan berbagai fungsi dan paket yang dapat digunakan untuk menghitung probabilitas, nilai harapan, variansi, dan melakukan berbagai uji statistik lainnya.
Keuntungan Penggunaan Software Statistik
Penggunaan software statistik untuk analisis peubah acak kontinu menawarkan beberapa keuntungan, yaitu:
- Kemudahan Penggunaan: Software statistik memiliki antarmuka yang ramah pengguna dan menyediakan berbagai fungsi yang mudah diakses, sehingga mempermudah analisis data.
- Efisiensi: Software statistik memungkinkan perhitungan yang kompleks dilakukan dengan cepat dan akurat, menghemat waktu dan tenaga.
- Visualisasi Data: Software statistik menyediakan berbagai alat untuk memvisualisasikan data, seperti histogram, boxplot, dan scatter plot. Visualisasi data membantu dalam memahami distribusi data dan pola yang mungkin ada.
- Kemampuan Analisis Lanjutan: Software statistik memungkinkan analisis yang lebih kompleks, seperti uji hipotesis, regresi, dan analisis multivariat.
Contoh Penggunaan Software Statistik
Sebagai contoh, kita dapat menggunakan software statistik seperti R untuk menganalisis data tinggi badan siswa di sebuah kelas. Asumsikan bahwa tinggi badan siswa mengikuti distribusi normal dengan rata-rata 170 cm dan standar deviasi 5 cm. Berikut adalah contoh kode R untuk menghitung probabilitas seorang siswa memiliki tinggi badan antara 165 cm dan 175 cm:
pnorm(175, mean = 170, sd = 5) – pnorm(165, mean = 170, sd = 5)
Kode ini akan menghasilkan probabilitas siswa memiliki tinggi badan antara 165 cm dan 175 cm. Software statistik juga dapat digunakan untuk menghitung nilai harapan dan variansi peubah acak kontinu.
Tutorial Singkat Penggunaan Software Statistik
Berikut adalah tutorial singkat untuk menggunakan software statistik R dalam menganalisis data peubah acak kontinu. Kita akan menggunakan dataset “iris” yang tersedia di R:
- Memuat Dataset: Pertama, kita perlu memuat dataset “iris” menggunakan fungsi
data(). - Menampilkan Data: Kita dapat menampilkan data menggunakan fungsi
head()atausummary(). - Membuat Histogram: Untuk melihat distribusi data, kita dapat membuat histogram menggunakan fungsi
hist(). - Menghitung Nilai Harapan: Nilai harapan dapat dihitung menggunakan fungsi
mean(). - Menghitung Variansi: Variansi dapat dihitung menggunakan fungsi
var().
Contoh kode R untuk melakukan langkah-langkah di atas:
data(iris)
head(iris)
summary(iris)
hist(iris$Sepal.Length)
mean(iris$Sepal.Length)
var(iris$Sepal.Length)
Kode ini akan menampilkan data, membuat histogram, menghitung nilai harapan, dan variansi untuk variabel “Sepal.Length” dalam dataset “iris”.
Contoh Soal Peubah Acak Kontinu dalam Konteks Riset
Peubah acak kontinu adalah variabel yang dapat mengambil nilai apa pun dalam rentang tertentu. Contohnya adalah tinggi badan, berat badan, suhu, dan tekanan darah. Dalam riset ilmiah, peubah acak kontinu sering digunakan untuk mengukur dan menganalisis data yang bersifat kuantitatif.
Contoh Soal Peubah Acak Kontinu dalam Riset Ilmiah
Misalnya, seorang peneliti ingin mempelajari pengaruh latihan fisik terhadap kadar kolesterol dalam darah. Dalam penelitian ini, kadar kolesterol adalah peubah acak kontinu yang dapat mengambil nilai apa pun dalam rentang tertentu. Peneliti dapat mengumpulkan data dari dua kelompok subjek: kelompok yang melakukan latihan fisik dan kelompok yang tidak. Kemudian, peneliti dapat menganalisis data untuk melihat apakah ada perbedaan signifikan dalam kadar kolesterol antara kedua kelompok.
Cara Mengumpulkan dan Menganalisis Data Peubah Acak Kontinu
Data peubah acak kontinu dapat dikumpulkan dengan berbagai cara, seperti melalui pengukuran, observasi, atau survei. Setelah data dikumpulkan, peneliti dapat menganalisis data menggunakan berbagai teknik statistik, seperti:
- Rata-rata
- Standar deviasi
- Uji t
- Analisis regresi
Teknik-teknik ini dapat membantu peneliti untuk memahami distribusi data, menguji hipotesis, dan menemukan hubungan antara variabel.
Contoh Interpretasi Hasil Analisis Data Peubah Acak Kontinu
Misalnya, peneliti menemukan bahwa rata-rata kadar kolesterol pada kelompok yang melakukan latihan fisik lebih rendah daripada kelompok yang tidak. Peneliti juga menemukan bahwa perbedaan rata-rata ini signifikan secara statistik. Berdasarkan hasil ini, peneliti dapat menyimpulkan bahwa latihan fisik dapat membantu menurunkan kadar kolesterol.
Penutupan Akhir: Contoh Soal Peubah Acak Kontinu
Memahami peubah acak kontinu tidak hanya penting untuk statistika, tetapi juga untuk berbagai bidang seperti ekonomi, ilmu komputer, dan kesehatan. Dengan mempelajari konsep ini, kita dapat memodelkan fenomena alam dan sosial, menganalisis data secara lebih mendalam, dan mengambil keputusan yang lebih baik.






