Contoh soal poligon – Pernahkah kamu memperhatikan bentuk-bentuk unik di sekitarmu? Bangunan, logo, hingga potongan kue, semuanya memiliki bentuk geometri yang menarik, termasuk poligon. Poligon, bentuk datar tertutup yang dibatasi oleh garis lurus, menyimpan banyak misteri dan keajaiban. Dari segitiga sederhana hingga poligon beraturan yang kompleks, dunia poligon menawarkan banyak hal untuk dipelajari.
Melalui contoh soal, kita akan menjelajahi berbagai aspek poligon, mulai dari definisi hingga rumus luas dan keliling. Kamu akan belajar menghitung sudut, menentukan jenis poligon, dan bahkan menerapkan konsep poligon dalam kehidupan sehari-hari. Siap untuk menjelajahi dunia poligon dan mengasah kemampuanmu dalam memecahkan soal?
Pengertian Poligon
Poligon adalah bentuk geometris dua dimensi yang terbentuk dari garis-garis lurus yang saling terhubung dan membentuk sisi-sisi tertutup. Bayangkan sebuah bentuk yang dibatasi oleh garis-garis lurus, seperti segitiga, persegi, atau bintang, itu adalah contoh poligon.
Contoh Poligon
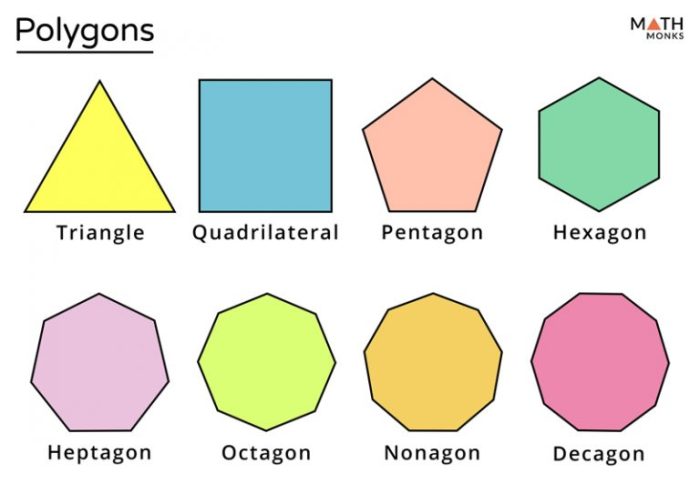
Poligon dapat berupa bentuk sederhana seperti segitiga, persegi, dan pentagon, atau bentuk kompleks seperti heksagon, oktagon, dan dekagon.
- Poligon Sederhana: Segitiga memiliki 3 sisi, persegi memiliki 4 sisi, dan pentagon memiliki 5 sisi.
- Poligon Kompleks: Heksagon memiliki 6 sisi, oktagon memiliki 8 sisi, dan dekagon memiliki 10 sisi.
Jenis-Jenis Poligon Berdasarkan Jumlah Sisi
Poligon diklasifikasikan berdasarkan jumlah sisinya. Berikut adalah beberapa jenis poligon yang umum:
| Nama Poligon | Jumlah Sisi |
|---|---|
| Segitiga | 3 |
| Segi Empat | 4 |
| Pentagon | 5 |
| Heksagon | 6 |
| Heptagon | 7 |
| Oktagon | 8 |
| Nonagon | 9 |
| Dekagon | 10 |
Sifat-Sifat Poligon
Poligon merupakan bangun datar yang dibatasi oleh garis lurus. Poligon memiliki beberapa sifat yang membedakannya dari bangun datar lainnya. Berikut ini beberapa sifat umum poligon yang perlu kamu ketahui.
Sifat Umum Poligon
Poligon memiliki beberapa sifat umum, di antaranya:
- Terdiri dari sisi-sisi yang merupakan garis lurus.
- Memiliki sudut-sudut yang terbentuk dari pertemuan dua sisi.
- Jumlah sisi dan jumlah sudutnya selalu sama.
- Poligon dapat dibagi menjadi beberapa segitiga dengan menarik diagonal dari salah satu titik sudutnya.
Poligon Cembung dan Cekung
Poligon dapat diklasifikasikan menjadi dua jenis, yaitu poligon cembung dan poligon cekung. Perbedaan keduanya terletak pada posisi sudut-sudutnya.
- Poligon cembung adalah poligon yang semua sudutnya kurang dari 180 derajat. Dengan kata lain, semua sudut dalam poligon cembung mengarah ke arah luar.
- Poligon cekung adalah poligon yang memiliki setidaknya satu sudut yang lebih besar dari 180 derajat. Artinya, terdapat sudut yang mengarah ke dalam poligon.
Sudut-Sudut Dalam Poligon
Jumlah sudut dalam poligon dapat dihitung dengan rumus:
(n – 2) x 180°
di mana n adalah jumlah sisi poligon.
Contohnya, untuk segitiga (n = 3), jumlah sudut dalam segitiga adalah (3 – 2) x 180° = 180°. Untuk persegi (n = 4), jumlah sudut dalam persegi adalah (4 – 2) x 180° = 360°.
Rumus Luas dan Keliling Poligon
Poligon adalah bangun datar tertutup yang dibatasi oleh ruas garis lurus. Ada berbagai macam bentuk poligon, mulai dari yang sederhana seperti segitiga dan persegi panjang hingga yang lebih kompleks seperti segi lima dan segi enam. Masing-masing poligon memiliki rumus luas dan keliling yang berbeda. Mari kita bahas rumus-rumus tersebut dan cara menghitungnya!
Rumus Luas dan Keliling Berbagai Bentuk Poligon
Rumus luas dan keliling poligon berbeda-beda tergantung pada bentuknya. Berikut adalah rumus untuk beberapa bentuk poligon yang umum:
- Segitiga
- Luas: 1/2 x alas x tinggi
- Keliling: sisi 1 + sisi 2 + sisi 3
- Persegi Panjang
- Luas: panjang x lebar
- Keliling: 2 x (panjang + lebar)
- Persegi
- Luas: sisi x sisi
- Keliling: 4 x sisi
- Trapesium
- Luas: 1/2 x (jumlah sisi sejajar) x tinggi
- Keliling: sisi 1 + sisi 2 + sisi 3 + sisi 4
- Layang-layang
- Luas: 1/2 x diagonal 1 x diagonal 2
- Keliling: sisi 1 + sisi 2 + sisi 3 + sisi 4
- Segi Lima
- Luas: 1/2 x keliling x apotema
- Keliling: sisi 1 + sisi 2 + sisi 3 + sisi 4 + sisi 5
- Segi Enam
- Luas: 1/2 x keliling x apotema
- Keliling: sisi 1 + sisi 2 + sisi 3 + sisi 4 + sisi 5 + sisi 6
Contoh Soal Perhitungan Luas dan Keliling Poligon
Berikut adalah contoh soal yang melibatkan perhitungan luas dan keliling poligon:
Sebuah segitiga memiliki alas 10 cm dan tinggi 6 cm. Hitunglah luas segitiga tersebut!
Penyelesaian:
Luas segitiga = 1/2 x alas x tinggi
Luas segitiga = 1/2 x 10 cm x 6 cm
Luas segitiga = 30 cm²
Sebuah persegi panjang memiliki panjang 8 cm dan lebar 5 cm. Hitunglah keliling persegi panjang tersebut!
Contoh soal poligon bisa jadi rumit, tapi bisa dipecahkan dengan strategi yang tepat. Misalnya, menghitung luas poligon tidak beraturan bisa melibatkan rumus yang berbeda. Nah, buat kamu yang suka tantangan, coba deh cari contoh soal sandi koordinat yang biasanya melibatkan pemahaman tentang posisi dan arah.
Soal sandi koordinat ini mirip dengan contoh soal poligon dalam hal membutuhkan ketelitian dan pemahaman konsep. Jadi, siap untuk mengasah otakmu dengan tantangan baru?
Penyelesaian:
Keliling persegi panjang = 2 x (panjang + lebar)
Keliling persegi panjang = 2 x (8 cm + 5 cm)
Keliling persegi panjang = 2 x 13 cm
Keliling persegi panjang = 26 cm
Langkah-Langkah Menghitung Luas dan Keliling Poligon
Berikut adalah langkah-langkah sistematis untuk menghitung luas dan keliling poligon:
- Tentukan bentuk poligon yang ingin dihitung luas dan kelilingnya.
- Identifikasi sisi-sisi dan sudut-sudut poligon tersebut.
- Pilih rumus yang tepat untuk menghitung luas dan keliling berdasarkan bentuk poligon.
- Masukkan nilai sisi-sisi dan sudut-sudut yang diketahui ke dalam rumus.
- Hitung luas dan keliling menggunakan operasi matematika yang diperlukan.
- Tuliskan hasil perhitungan dengan satuan yang sesuai.
Jenis-Jenis Poligon Khusus
Poligon adalah bentuk geometris dua dimensi yang dibatasi oleh garis-garis lurus yang saling terhubung. Ada berbagai jenis poligon khusus, dengan ciri dan sifat uniknya masing-masing. Jenis-jenis poligon khusus ini memiliki peran penting dalam berbagai bidang, mulai dari arsitektur hingga ilmu komputer.
Segitiga, Contoh soal poligon
Segitiga adalah poligon dengan tiga sisi dan tiga sudut. Segitiga merupakan salah satu bentuk geometris paling dasar dan memiliki banyak sifat unik. Berikut adalah beberapa jenis segitiga yang umum:
- Segitiga sama sisi: Ketiga sisinya sama panjang dan ketiga sudutnya sama besar (60 derajat).
- Segitiga sama kaki: Dua sisinya sama panjang dan dua sudutnya sama besar.
- Segitiga siku-siku: Salah satu sudutnya adalah sudut siku-siku (90 derajat).
Persegi
Persegi adalah poligon dengan empat sisi yang sama panjang dan empat sudut siku-siku. Persegi merupakan contoh khusus dari segi empat, yaitu poligon dengan empat sisi. Berikut adalah beberapa sifat persegi:
- Semua sisinya sama panjang.
- Semua sudutnya siku-siku.
- Diagonalnya saling berpotongan tegak lurus dan membagi persegi menjadi empat segitiga siku-siku kongruen.
Persegi Panjang
Persegi panjang adalah poligon dengan empat sisi dan empat sudut siku-siku. Perbedaan utama antara persegi dan persegi panjang adalah panjang sisi yang berhadapan sama, tetapi tidak semua sisinya sama panjang. Berikut adalah beberapa sifat persegi panjang:
- Sisi yang berhadapan sejajar dan sama panjang.
- Semua sudutnya siku-siku.
- Diagonalnya saling berpotongan di tengah persegi panjang.
Lingkaran
Lingkaran adalah kumpulan semua titik yang berjarak sama dari titik tetap yang disebut pusat. Meskipun lingkaran bukan poligon karena tidak dibatasi oleh garis lurus, namun sering kali dipelajari bersama dengan poligon karena memiliki banyak aplikasi praktis. Berikut adalah beberapa sifat lingkaran:
- Semua titik pada lingkaran berjarak sama dari pusatnya.
- Lingkaran memiliki keliling, yaitu jarak mengelilingi lingkaran.
- Lingkaran memiliki luas, yaitu area yang dikurung oleh lingkaran.
| Jenis Poligon | Contoh Soal |
|---|---|
| Segitiga | Sebuah segitiga memiliki sisi-sisi dengan panjang 5 cm, 7 cm, dan 8 cm. Hitung keliling segitiga tersebut. |
| Persegi | Sebuah persegi memiliki sisi dengan panjang 10 cm. Hitung luas persegi tersebut. |
| Persegi Panjang | Sebuah persegi panjang memiliki panjang 12 cm dan lebar 8 cm. Hitung keliling persegi panjang tersebut. |
| Lingkaran | Sebuah lingkaran memiliki jari-jari 5 cm. Hitung luas lingkaran tersebut. |
Penerapan Poligon dalam Kehidupan Sehari-hari
Poligon, bentuk geometris yang terdiri dari garis-garis lurus yang saling terhubung, bukan hanya konsep abstrak yang dipelajari di kelas matematika. Poligon hadir dalam berbagai bentuk dan ukuran, dan berperan penting dalam berbagai aspek kehidupan kita. Dari bangunan yang kita tinggali hingga seni yang kita nikmati, poligon menjadi dasar dari banyak desain dan struktur di sekitar kita.
Aplikasi Poligon dalam Arsitektur, Desain, dan Seni
Arsitektur, desain, dan seni merupakan bidang yang sangat dipengaruhi oleh penggunaan poligon. Bentuk-bentuk geometris ini memungkinkan para arsitek, desainer, dan seniman untuk menciptakan struktur yang kokoh, estetis, dan fungsional.
- Dalam arsitektur, poligon digunakan dalam perencanaan dan konstruksi bangunan. Misalnya, bentuk persegi panjang dan segitiga sering digunakan dalam desain rumah, gedung perkantoran, dan jembatan. Penggunaan poligon ini tidak hanya memastikan stabilitas struktur, tetapi juga memungkinkan penciptaan ruang yang efisien dan estetis.
- Di bidang desain, poligon memainkan peran penting dalam berbagai desain produk, mulai dari pakaian hingga furnitur. Desainer menggunakan bentuk poligon untuk menciptakan produk yang ergonomis, menarik, dan mudah digunakan. Misalnya, bentuk persegi panjang dan segitiga sering digunakan dalam desain kursi, meja, dan lemari.
- Dalam seni, poligon telah digunakan selama berabad-abad untuk menciptakan karya seni yang menakjubkan. Seniman menggunakan poligon untuk menciptakan efek perspektif, tekstur, dan komposisi yang menarik. Misalnya, dalam lukisan perspektif, poligon digunakan untuk menciptakan ilusi ruang dan kedalaman.
Penggunaan Poligon dalam Pengukuran dan Pemetaan
Poligon juga berperan penting dalam pengukuran dan pemetaan. Bentuk-bentuk geometris ini memungkinkan para surveyor dan ahli pemetaan untuk mengukur jarak, luas, dan bentuk area tertentu dengan akurat.
- Dalam pengukuran tanah, poligon digunakan untuk membagi lahan menjadi bagian-bagian yang lebih kecil, untuk tujuan perencanaan dan pembangunan.
- Dalam pemetaan, poligon digunakan untuk menggambarkan bentuk dan ukuran wilayah tertentu. Misalnya, peta jalan menggunakan poligon untuk mewakili jalan, sungai, dan bangunan.
- Penggunaan poligon dalam pemetaan juga memungkinkan para ahli untuk mengukur luas area tertentu, yang penting untuk berbagai keperluan seperti perencanaan kota, pengelolaan sumber daya, dan analisis lingkungan.
Soal Latihan Poligon
Setelah mempelajari konsep, sifat, dan rumus poligon, mari kita uji pemahamanmu dengan beberapa soal latihan. Soal-soal ini dirancang untuk mengasah kemampuanmu dalam menerapkan pengetahuan tentang poligon dalam berbagai situasi.
Konsep dan Sifat Poligon
Soal-soal berikut menguji pemahamanmu tentang definisi, jenis, dan sifat dasar poligon.
- Jelaskan perbedaan antara poligon cembung dan cekung. Berikan contoh masing-masing.
- Sebutkan jenis-jenis poligon berdasarkan jumlah sisinya. Berikan contoh masing-masing.
- Jelaskan konsep diagonal pada poligon. Bagaimana cara menghitung jumlah diagonal pada poligon beraturan dengan n sisi?
- Apa yang dimaksud dengan poligon beraturan? Sebutkan beberapa sifat yang dimiliki poligon beraturan.
Rumus Poligon
Soal-soal berikut menguji pemahamanmu dalam menerapkan rumus untuk menghitung keliling, luas, dan jumlah sudut pada poligon.
- Sebuah persegi panjang memiliki panjang 10 cm dan lebar 5 cm. Hitunglah keliling dan luas persegi panjang tersebut.
- Sebuah segitiga sama sisi memiliki panjang sisi 6 cm. Hitunglah keliling dan luas segitiga tersebut.
- Sebuah poligon beraturan memiliki 8 sisi dan panjang sisi 5 cm. Hitunglah jumlah sudut interior dan jumlah sudut eksterior poligon tersebut.
Soal Cerita
Soal-soal berikut menguji kemampuanmu dalam menerapkan konsep poligon dalam konteks nyata.
- Sebuah taman berbentuk persegi panjang dengan panjang 20 meter dan lebar 15 meter. Di tengah taman terdapat kolam berbentuk lingkaran dengan diameter 5 meter. Hitunglah luas taman yang tersisa setelah dikurangi luas kolam.
- Sebuah lantai berbentuk persegi dengan panjang sisi 5 meter. Di tengah lantai terdapat ubin berbentuk segitiga sama sisi dengan panjang sisi 1 meter. Hitunglah jumlah ubin yang dibutuhkan untuk menutupi seluruh lantai.
- Sebuah rumah berbentuk persegi panjang dengan panjang 12 meter dan lebar 8 meter. Di bagian depan rumah terdapat teras berbentuk segitiga siku-siku dengan panjang sisi miring 5 meter. Hitunglah luas teras tersebut.
Poligon Beraturan
Poligon beraturan adalah poligon yang memiliki semua sisi dan sudut yang sama besar. Poligon beraturan memiliki bentuk yang simetris dan teratur, sehingga mudah diidentifikasi dan dipelajari.
Ciri-ciri Poligon Beraturan
Berikut adalah ciri-ciri yang membedakan poligon beraturan dengan poligon lainnya:
- Semua sisi memiliki panjang yang sama.
- Semua sudut memiliki ukuran yang sama.
- Poligon beraturan memiliki sumbu simetri yang sama banyaknya dengan jumlah sisinya.
- Semua titik sudut poligon beraturan terletak pada lingkaran yang sama, yang disebut lingkaran luar.
- Semua sisi poligon beraturan menyinggung lingkaran yang sama, yang disebut lingkaran dalam.
Contoh Soal Perhitungan Sudut Dalam Poligon Beraturan
Misalnya, kita ingin menghitung besar sudut dalam sebuah segi enam beraturan. Kita tahu bahwa jumlah sudut dalam segi enam adalah (6-2) x 180 = 720 derajat. Karena semua sudut dalam segi enam beraturan sama besar, maka besar setiap sudut adalah 720/6 = 120 derajat.
Perbedaan Poligon Beraturan dan Tidak Beraturan
Poligon tidak beraturan adalah poligon yang tidak memiliki semua sisi dan sudut yang sama besar. Berikut adalah ilustrasi perbedaan antara poligon beraturan dan tidak beraturan:
Poligon Beraturan: Semua sisi dan sudut memiliki ukuran yang sama, bentuknya simetris dan teratur.
Poligon Tidak Beraturan: Sisi dan sudut memiliki ukuran yang berbeda, bentuknya tidak simetris dan tidak teratur.
Sebagai contoh, persegi adalah poligon beraturan karena keempat sisinya sama panjang dan keempat sudutnya sama besar. Sementara itu, persegi panjang adalah poligon tidak beraturan karena dua sisi panjangnya berbeda dengan dua sisi pendeknya.
Poligon Tidak Beraturan
Poligon tidak beraturan merupakan poligon yang memiliki sisi-sisi dengan panjang yang tidak sama dan sudut-sudut yang tidak sama besarnya. Berbeda dengan poligon beraturan yang memiliki sisi dan sudut yang sama besar, poligon tidak beraturan memiliki bentuk yang lebih beragam dan kompleks.
Ciri-ciri Poligon Tidak Beraturan
Poligon tidak beraturan memiliki beberapa ciri khas yang membedakannya dari poligon beraturan. Berikut adalah beberapa ciri-cirinya:
- Sisi-sisi poligon tidak beraturan memiliki panjang yang berbeda-beda.
- Sudut-sudut poligon tidak beraturan memiliki ukuran yang berbeda-beda.
- Tidak semua sudut poligon tidak beraturan memiliki besar yang sama.
- Poligon tidak beraturan memiliki bentuk yang tidak simetris.
Contoh Soal Poligon Tidak Beraturan
Berikut adalah contoh soal yang melibatkan perhitungan luas dan keliling poligon tidak beraturan:
Sebuah taman berbentuk poligon tidak beraturan memiliki sisi-sisi dengan panjang sebagai berikut: 10 meter, 8 meter, 6 meter, 5 meter, dan 7 meter. Jika sudut-sudut taman tersebut adalah 90 derajat, 120 derajat, 60 derajat, 100 derajat, dan 110 derajat, tentukan luas dan keliling taman tersebut.
Langkah-langkah Menghitung Luas dan Keliling Poligon Tidak Beraturan
| Langkah | Luas | Keliling |
|---|---|---|
| 1 | Bagi poligon tidak beraturan menjadi beberapa bentuk geometri sederhana seperti segitiga, persegi panjang, atau trapesium. | Jumlahkan panjang semua sisi poligon tidak beraturan. |
| 2 | Hitung luas masing-masing bentuk geometri sederhana yang telah dibagi. | – |
| 3 | Jumlahkan luas semua bentuk geometri sederhana untuk mendapatkan luas total poligon tidak beraturan. | – |
Diagonal Poligon
Poligon merupakan bangun datar yang dibatasi oleh garis-garis lurus. Dalam geometri, diagonal poligon adalah garis lurus yang menghubungkan dua titik sudut yang tidak berdekatan pada poligon. Pengertian ini penting untuk memahami sifat-sifat poligon dan menghitung jumlah diagonalnya.
Jumlah Diagonal dalam Poligon
Jumlah diagonal dalam poligon dapat dihitung dengan rumus:
n(n-3)/2
Dimana n adalah jumlah sisi poligon. Rumus ini dapat digunakan untuk menentukan jumlah diagonal dalam poligon dengan jumlah sisi berapa pun.
Contoh Soal
Misalnya, kita ingin menentukan jumlah diagonal dalam segi enam (heksagon). Segi enam memiliki 6 sisi (n = 6). Dengan menggunakan rumus di atas, kita dapat menghitung jumlah diagonalnya:
- n(n-3)/2 = 6(6-3)/2 = 6(3)/2 = 9
Jadi, segi enam memiliki 9 diagonal.
Ilustrasi Diagonal dalam Poligon
Untuk lebih memahami konsep diagonal, perhatikan ilustrasi berikut. Gambar di bawah menunjukkan sebuah segi lima (pentagon) dengan diagonal-diagonalnya.
Dalam ilustrasi ini, kita dapat melihat bahwa segi lima memiliki 5 sisi dan 5 diagonal. Diagonal-diagonal ini menghubungkan titik-titik sudut yang tidak berdekatan pada segi lima. Dengan memahami konsep diagonal dan rumus perhitungannya, kita dapat menganalisis dan memahami sifat-sifat poligon dengan lebih baik.
Poligon dan Simetri: Contoh Soal Poligon
Poligon adalah bentuk geometri dua dimensi yang dibentuk oleh garis-garis lurus yang saling terhubung. Simetri dalam poligon merujuk pada kesamaan bentuk dan ukuran pada kedua sisi garis, titik, atau bidang tertentu. Poligon dapat memiliki berbagai jenis simetri, yang dibedakan berdasarkan bagaimana bentuknya dapat dibagi menjadi bagian-bagian yang sama.
Jenis-jenis Simetri pada Poligon
Simetri dalam poligon dapat diklasifikasikan menjadi dua jenis utama:
- Simetri Garis (Simetri Bilateral): Poligon memiliki simetri garis jika dapat dilipat menjadi dua bagian yang sama persis sepanjang garis tertentu. Garis ini disebut sumbu simetri.
- Simetri Putar (Simetri Rotasi): Poligon memiliki simetri putar jika dapat diputar pada titik pusatnya sehingga tampak sama dengan bentuk aslinya. Jumlah derajat putaran yang diperlukan untuk kembali ke bentuk aslinya disebut orde simetri putar.
Contoh Soal
Perhatikan poligon berikut:
Gambarlah poligon dan tentukan jenis simetri yang dimilikinya.
Berikut contoh poligon dengan simetri yang berbeda:
| Poligon | Simetri Garis | Simetri Putar |
|---|---|---|
| Segitiga Sama Sisi | 3 | 3 |
| Segi Empat Persegi Panjang | 2 | 2 |
| Segi Empat Persegi | 4 | 4 |
| Pentagon Beraturan | 5 | 5 |
Poligon dan Transformasi Geometri
Poligon, bentuk geometris tertutup yang dibentuk oleh garis lurus, dapat diubah bentuk dan posisinya melalui transformasi geometri. Transformasi ini melibatkan manipulasi geometrik, seperti menggeser, memutar, atau mencerminkan poligon, tanpa mengubah ukuran atau bentuk aslinya. Artikel ini akan membahas pengaruh transformasi geometri, seperti translasi, rotasi, dan refleksi, pada poligon, disertai dengan contoh soal dan ilustrasi untuk memperjelas konsepnya.
Pengaruh Transformasi Geometri pada Poligon
Transformasi geometri memiliki dampak signifikan pada poligon, mengubah posisi, orientasi, atau keduanya. Tiga jenis transformasi utama yang memengaruhi poligon adalah:
- Translasi: Translasi adalah pergeseran poligon tanpa mengubah bentuk atau orientasinya. Ini dilakukan dengan memindahkan setiap titik pada poligon dengan jarak dan arah yang sama. Sebagai contoh, jika sebuah segitiga digeser 3 satuan ke kanan dan 2 satuan ke atas, setiap titik pada segitiga akan bergerak 3 satuan ke kanan dan 2 satuan ke atas.
- Rotasi: Rotasi adalah perputaran poligon di sekitar titik tetap yang disebut pusat rotasi. Rotasi melibatkan mengubah orientasi poligon tanpa mengubah bentuk atau ukurannya. Sudut rotasi menentukan seberapa jauh poligon diputar. Sebagai contoh, jika sebuah persegi diputar 90 derajat searah jarum jam di sekitar pusatnya, setiap titik pada persegi akan bergerak 90 derajat searah jarum jam di sekitar pusat tersebut.
- Refleksi: Refleksi adalah pencerminan poligon terhadap garis lurus yang disebut sumbu refleksi. Refleksi menghasilkan bayangan cermin dari poligon asli, di mana setiap titik pada poligon terletak pada jarak yang sama dari sumbu refleksi seperti titik yang sesuai pada bayangannya. Sebagai contoh, jika sebuah segitiga direfleksikan terhadap sumbu vertikal, setiap titik pada segitiga akan bergerak ke sisi lain dari sumbu vertikal, pada jarak yang sama dari sumbu tersebut.
Contoh Soal Transformasi Geometri pada Poligon
Misalnya, perhatikan persegi ABCD dengan titik-titik A(1, 1), B(3, 1), C(3, 3), dan D(1, 3). Jika persegi ABCD ditranslasikan 2 satuan ke kanan dan 1 satuan ke bawah, maka titik-titik baru pada persegi tersebut akan menjadi:
| Titik Asli | Translasi | Titik Baru |
|---|---|---|
| A(1, 1) | (1 + 2, 1 – 1) | A'(3, 0) |
| B(3, 1) | (3 + 2, 1 – 1) | B'(5, 0) |
| C(3, 3) | (3 + 2, 3 – 1) | C'(5, 2) |
| D(1, 3) | (1 + 2, 3 – 1) | D'(3, 2) |
Ilustrasi Transformasi Geometri pada Poligon
Ilustrasi berikut menunjukkan hasil transformasi geometri pada poligon. Gambar tersebut menampilkan sebuah segitiga ABC yang ditranslasikan 3 satuan ke kanan dan 2 satuan ke atas, diputar 90 derajat searah jarum jam di sekitar titik A, dan direfleksikan terhadap sumbu vertikal.
Translasi: Segitiga ABC digeser 3 satuan ke kanan dan 2 satuan ke atas, menghasilkan segitiga A’B’C’.
Rotasi: Segitiga A’B’C’ diputar 90 derajat searah jarum jam di sekitar titik A’, menghasilkan segitiga A”B”C”.
Refleksi: Segitiga A”B”C” direfleksikan terhadap sumbu vertikal, menghasilkan segitiga A”’B”’C”’.
Penutupan Akhir
Memahami konsep poligon tidak hanya penting dalam dunia matematika, tetapi juga dalam berbagai bidang kehidupan. Dari arsitektur hingga desain grafis, pemahaman tentang poligon membantu kita menciptakan bentuk-bentuk yang indah dan fungsional. Dengan contoh soal yang beragam, kamu dapat meningkatkan kemampuanmu dalam memahami dan menerapkan konsep poligon dalam berbagai situasi.




