Contoh soal probabilitas statistika dan penyelesaiannya – Pernahkah Anda bertanya-tanya bagaimana peluang Anda untuk mendapatkan nilai A pada ujian, atau seberapa besar kemungkinan Anda akan memenangkan lotere? Contoh Soal Probabilitas dan Statistika: Memahami Peluang dan Data akan membantu Anda memahami konsep-konsep dasar probabilitas dan statistika yang sering kita temui dalam kehidupan sehari-hari.
Dari memahami peluang mendapatkan kartu As dalam permainan kartu hingga menganalisis data penjualan produk, probabilitas dan statistika memiliki peran penting dalam berbagai bidang. Artikel ini akan membahas berbagai jenis probabilitas, aturan dasar, dan contoh soal yang disertai penyelesaiannya. Selain itu, kita juga akan melihat bagaimana probabilitas dan statistika saling terkait dan bagaimana keduanya diterapkan dalam kehidupan nyata.
Pengertian Probabilitas dan Statistika
Probabilitas dan statistika merupakan dua konsep matematika yang saling terkait erat dan memainkan peran penting dalam berbagai bidang, mulai dari ilmu pengetahuan dan teknologi hingga pengambilan keputusan dalam kehidupan sehari-hari. Probabilitas membantu kita memahami kemungkinan terjadinya suatu peristiwa, sedangkan statistika memberikan metode untuk mengumpulkan, menganalisis, dan menginterpretasikan data.
Konsep Probabilitas dalam Statistika
Probabilitas dalam statistika mengacu pada ukuran kemungkinan terjadinya suatu peristiwa. Secara sederhana, probabilitas adalah angka antara 0 dan 1, di mana 0 mewakili peristiwa yang tidak mungkin terjadi dan 1 mewakili peristiwa yang pasti terjadi. Semakin tinggi nilai probabilitas, semakin besar kemungkinan peristiwa tersebut terjadi.
Contoh Peristiwa Probabilistik
Contoh sederhana dari peristiwa probabilistik adalah melempar koin. Ketika kita melempar koin, ada dua kemungkinan hasil: sisi kepala (H) atau sisi ekor (T). Probabilitas mendapatkan sisi kepala adalah 1/2, karena ada satu hasil yang menguntungkan (sisi kepala) dari dua hasil yang mungkin (kepala atau ekor). Demikian pula, probabilitas mendapatkan sisi ekor juga 1/2.
Perbedaan Probabilitas dan Statistika
Meskipun saling terkait, probabilitas dan statistika memiliki perbedaan yang jelas. Probabilitas berfokus pada kemungkinan terjadinya suatu peristiwa, sedangkan statistika lebih luas, mencakup pengumpulan, analisis, dan interpretasi data untuk menarik kesimpulan dan membuat prediksi.
- Probabilitas berfokus pada kemungkinan suatu peristiwa terjadi, dihitung berdasarkan informasi yang diketahui.
- Statistika melibatkan pengumpulan, analisis, dan interpretasi data untuk memahami pola, tren, dan hubungan dalam data.
Aturan Dasar Probabilitas: Contoh Soal Probabilitas Statistika Dan Penyelesaiannya
Probabilitas merupakan konsep dasar dalam statistika yang membahas tentang kemungkinan terjadinya suatu peristiwa. Dalam menghitung probabilitas, kita perlu memahami aturan-aturan dasar yang mengatur bagaimana kemungkinan suatu peristiwa dapat dihitung. Dua aturan dasar yang penting dalam probabilitas adalah aturan penjumlahan dan aturan perkalian.
Aturan Penjumlahan
Aturan penjumlahan digunakan untuk menghitung probabilitas gabungan dari dua peristiwa yang saling eksklusif. Artinya, kedua peristiwa tidak dapat terjadi secara bersamaan. Rumus aturan penjumlahan adalah:
P(A atau B) = P(A) + P(B)
Dimana:
- P(A atau B) adalah probabilitas terjadinya peristiwa A atau peristiwa B.
- P(A) adalah probabilitas terjadinya peristiwa A.
- P(B) adalah probabilitas terjadinya peristiwa B.
Contoh Penerapan Aturan Penjumlahan
Misalnya, dalam pelemparan sebuah dadu, kita ingin menghitung probabilitas mendapatkan angka genap atau angka lebih besar dari 4. Peristiwa mendapatkan angka genap (A) dan peristiwa mendapatkan angka lebih besar dari 4 (B) adalah saling eksklusif karena tidak mungkin mendapatkan angka genap dan lebih besar dari 4 secara bersamaan.
Probabilitas mendapatkan angka genap adalah 3/6 (karena ada 3 angka genap: 2, 4, dan 6), dan probabilitas mendapatkan angka lebih besar dari 4 adalah 2/6 (karena ada 2 angka lebih besar dari 4: 5 dan 6). Maka, probabilitas mendapatkan angka genap atau angka lebih besar dari 4 adalah:
P(A atau B) = P(A) + P(B) = 3/6 + 2/6 = 5/6
Aturan Perkalian
Aturan perkalian digunakan untuk menghitung probabilitas gabungan dari dua peristiwa yang saling independen. Artinya, terjadinya satu peristiwa tidak mempengaruhi terjadinya peristiwa lainnya. Rumus aturan perkalian adalah:
P(A dan B) = P(A) * P(B)
Dimana:
- P(A dan B) adalah probabilitas terjadinya peristiwa A dan peristiwa B.
- P(A) adalah probabilitas terjadinya peristiwa A.
- P(B) adalah probabilitas terjadinya peristiwa B.
Contoh Penerapan Aturan Perkalian, Contoh soal probabilitas statistika dan penyelesaiannya
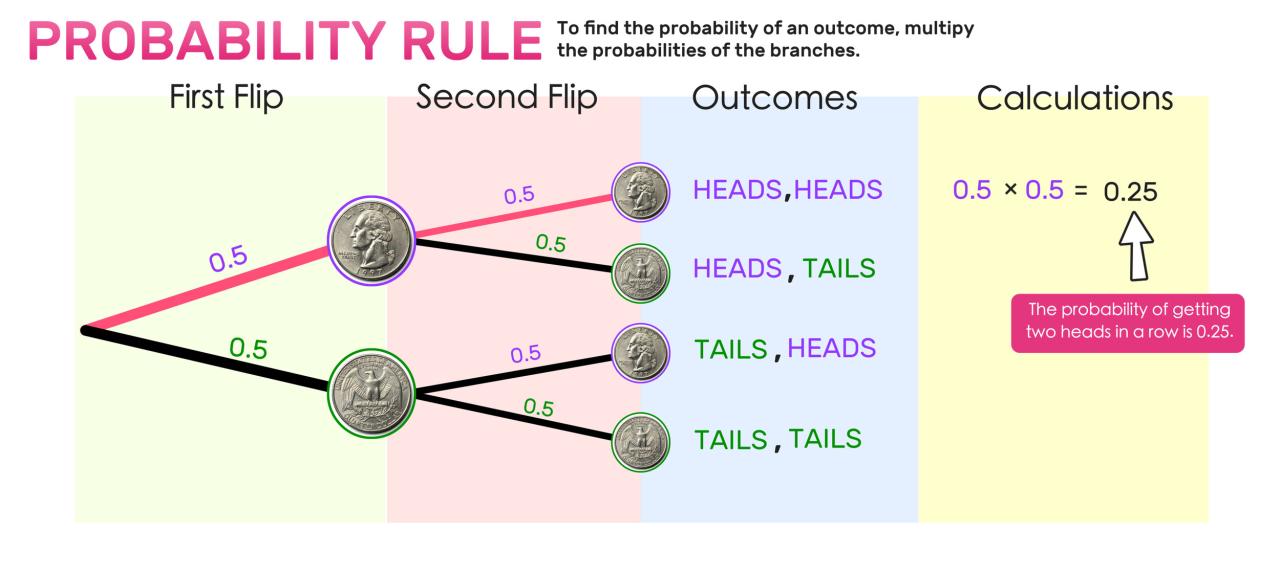
Misalnya, kita ingin menghitung probabilitas mendapatkan sisi kepala pada pelemparan koin pertama dan sisi kepala pada pelemparan koin kedua. Kedua pelemparan koin adalah independen, karena hasil pada pelemparan pertama tidak mempengaruhi hasil pada pelemparan kedua.
Probabilitas mendapatkan sisi kepala pada pelemparan pertama adalah 1/2, dan probabilitas mendapatkan sisi kepala pada pelemparan kedua juga 1/2. Maka, probabilitas mendapatkan sisi kepala pada kedua pelemparan adalah:
P(A dan B) = P(A) * P(B) = 1/2 * 1/2 = 1/4
Distribusi Probabilitas
Distribusi probabilitas merupakan konsep penting dalam statistika yang menggambarkan kemungkinan terjadinya suatu peristiwa atau hasil dalam suatu ruang sampel. Distribusi ini menunjukkan bagaimana probabilitas tersebar di antara berbagai nilai yang mungkin dari suatu variabel acak.
Jenis-Jenis Distribusi Probabilitas
Terdapat banyak jenis distribusi probabilitas, yang masing-masing memiliki karakteristik dan rumus yang berbeda. Berikut adalah beberapa contoh distribusi probabilitas yang umum digunakan:
- Distribusi Bernoulli: Distribusi ini menggambarkan probabilitas sukses atau gagal dalam suatu percobaan tunggal.
- Distribusi Binomial: Distribusi ini menggambarkan probabilitas jumlah keberhasilan dalam serangkaian percobaan Bernoulli yang independen.
- Distribusi Poisson: Distribusi ini menggambarkan probabilitas jumlah peristiwa yang terjadi dalam suatu periode waktu atau ruang tertentu.
- Distribusi Normal: Distribusi ini merupakan distribusi probabilitas yang paling umum digunakan dalam statistika. Distribusi normal berbentuk lonceng dan simetris, dengan probabilitas terbesar di tengah dan probabilitas yang semakin kecil semakin jauh dari tengah.
- Distribusi Eksponensial: Distribusi ini menggambarkan probabilitas waktu antara dua peristiwa yang terjadi secara acak.
- Distribusi Uniform: Distribusi ini menggambarkan probabilitas yang sama untuk setiap nilai dalam rentang tertentu.
Tabel Karakteristik Distribusi Probabilitas
| Distribusi | Karakteristik | Rumus |
|---|---|---|
| Bernoulli | – Percobaan tunggal dengan dua hasil: sukses atau gagal. – Probabilitas sukses (p) dan probabilitas gagal (q) tetap konstan. |
P(X = k) = p^k * q^(1-k), dimana k = 0 atau 1 |
| Binomial | – Serangkaian percobaan Bernoulli yang independen. – Probabilitas sukses (p) dan probabilitas gagal (q) tetap konstan. |
P(X = k) = (nCk) * p^k * q^(n-k), dimana n adalah jumlah percobaan, k adalah jumlah keberhasilan. |
| Poisson | – Menggambarkan jumlah peristiwa yang terjadi dalam periode waktu atau ruang tertentu. – Rata-rata jumlah peristiwa (λ) tetap konstan. |
P(X = k) = (e^(-λ) * λ^k) / k!, dimana k adalah jumlah peristiwa. |
| Normal | – Distribusi simetris berbentuk lonceng. – Rata-rata (μ) dan deviasi standar (σ) menentukan bentuk dan lokasi distribusi. |
f(x) = (1 / (σ * √(2π))) * e^(-(x-μ)^2 / (2σ^2)), dimana x adalah nilai variabel acak. |
| Eksponensial | – Menggambarkan waktu antara dua peristiwa yang terjadi secara acak. – Rata-rata waktu antara peristiwa (λ) tetap konstan. |
f(x) = λ * e^(-λx), dimana x adalah waktu antara peristiwa. |
| Uniform | – Probabilitas yang sama untuk setiap nilai dalam rentang tertentu. | f(x) = 1 / (b – a), dimana a dan b adalah batas bawah dan atas rentang. |
Contoh Soal Probabilitas dan Penyelesaiannya
Probabilitas merupakan konsep penting dalam statistika yang mempelajari tentang kemungkinan terjadinya suatu kejadian. Peluang suatu kejadian dapat dinyatakan dalam bentuk pecahan, desimal, atau persentase. Dalam artikel ini, kita akan membahas beberapa contoh soal probabilitas dan penyelesaiannya untuk membantu Anda memahami konsep ini dengan lebih baik.
Contoh Soal Probabilitas Kejadian Tunggal
Kejadian tunggal adalah kejadian yang hanya melibatkan satu peristiwa. Untuk menghitung peluang kejadian tunggal, kita perlu mengetahui jumlah total kemungkinan hasil dan jumlah hasil yang diinginkan.
- Misalnya, sebuah dadu dilempar sekali. Berapakah peluang munculnya mata dadu 6?
Penyelesaian:
- Jumlah total kemungkinan hasil adalah 6, karena dadu memiliki 6 sisi.
- Jumlah hasil yang diinginkan adalah 1, yaitu munculnya mata dadu 6.
- Maka, peluang munculnya mata dadu 6 adalah 1/6.
Contoh Soal Probabilitas Kejadian Majemuk
Kejadian majemuk adalah kejadian yang melibatkan lebih dari satu peristiwa. Untuk menghitung peluang kejadian majemuk, kita perlu mempertimbangkan semua kemungkinan hasil dari setiap peristiwa.
- Misalnya, sebuah koin dilempar dua kali. Berapakah peluang munculnya sisi gambar pada lemparan pertama dan sisi angka pada lemparan kedua?
Penyelesaian:
- Peluang munculnya sisi gambar pada lemparan pertama adalah 1/2.
- Peluang munculnya sisi angka pada lemparan kedua adalah 1/2.
- Karena kedua peristiwa ini independen (tidak saling mempengaruhi), maka peluang kejadian majemuk ini adalah hasil kali dari peluang masing-masing peristiwa: (1/2) * (1/2) = 1/4.
Langkah-Langkah Penyelesaian Soal Probabilitas
Berikut adalah langkah-langkah umum dalam menyelesaikan soal probabilitas:
- Tentukan ruang sampel, yaitu himpunan semua kemungkinan hasil.
- Tentukan kejadian yang ingin dihitung peluangnya.
- Hitung jumlah hasil yang diinginkan.
- Hitung jumlah total kemungkinan hasil.
- Hitung peluang kejadian dengan membagi jumlah hasil yang diinginkan dengan jumlah total kemungkinan hasil.
Contoh Penyelesaian Soal Probabilitas
Sebuah kotak berisi 5 bola merah, 3 bola biru, dan 2 bola hijau. Sebuah bola diambil secara acak dari kotak. Berapakah peluang terambilnya bola merah?
Penyelesaian:
- Ruang sampel adalah merah, biru, hijau.
- Kejadian yang ingin dihitung peluangnya adalah terambilnya bola merah.
- Jumlah hasil yang diinginkan adalah 5, karena ada 5 bola merah.
- Jumlah total kemungkinan hasil adalah 10, karena ada 10 bola dalam kotak.
- Peluang terambilnya bola merah adalah 5/10 = 1/2.
Aplikasi Probabilitas dalam Kehidupan Sehari-hari
Probabilitas merupakan konsep dasar dalam statistika yang memiliki aplikasi luas dalam berbagai aspek kehidupan. Probabilitas membantu kita memahami kemungkinan suatu peristiwa terjadi, dan ini sangat berguna dalam pengambilan keputusan, perencanaan, dan prediksi.
Aplikasi Probabilitas dalam Bidang Kesehatan
Probabilitas memainkan peran penting dalam bidang kesehatan, khususnya dalam analisis data klinis, pengambilan keputusan medis, dan pengembangan pengobatan.
- Analisis Data Klinis: Probabilitas digunakan untuk menganalisis data klinis dan memahami pola penyakit, efektivitas pengobatan, dan faktor risiko. Misalnya, dengan menggunakan probabilitas, para peneliti dapat menentukan kemungkinan seseorang terkena penyakit tertentu berdasarkan faktor-faktor seperti usia, jenis kelamin, dan riwayat keluarga.
- Pengambilan Keputusan Medis: Probabilitas membantu para dokter dalam pengambilan keputusan medis, seperti memilih pengobatan yang paling tepat berdasarkan kemungkinan keberhasilan dan efek sampingnya. Misalnya, dokter dapat mempertimbangkan probabilitas kesembuhan pasien dengan menggunakan metode pengobatan tertentu dibandingkan dengan metode lain.
- Pengembangan Pengobatan: Probabilitas digunakan dalam pengembangan pengobatan baru, seperti dalam uji klinis untuk menentukan efektivitas dan keamanan obat baru. Probabilitas membantu para peneliti dalam menilai kemungkinan keberhasilan pengobatan dan meminimalkan risiko efek samping.
Aplikasi Probabilitas dalam Bidang Ekonomi
Probabilitas memiliki aplikasi yang luas dalam bidang ekonomi, khususnya dalam analisis pasar keuangan, manajemen risiko, dan perencanaan investasi.
- Analisis Pasar Keuangan: Probabilitas digunakan untuk menganalisis data pasar keuangan dan memprediksi pergerakan harga saham, mata uang, dan aset lainnya. Misalnya, para analis keuangan menggunakan probabilitas untuk menilai kemungkinan keuntungan atau kerugian dari suatu investasi.
- Manajemen Risiko: Probabilitas membantu perusahaan dalam mengelola risiko bisnis, seperti risiko kerugian akibat bencana alam, fluktuasi harga, atau perubahan kebijakan pemerintah. Misalnya, perusahaan asuransi menggunakan probabilitas untuk menghitung premi asuransi berdasarkan kemungkinan klaim.
- Perencanaan Investasi: Probabilitas digunakan dalam perencanaan investasi untuk menentukan strategi investasi yang optimal berdasarkan kemungkinan pengembalian dan risiko. Misalnya, investor dapat menggunakan probabilitas untuk memilih portofolio investasi yang sesuai dengan toleransi risiko mereka.
Aplikasi Probabilitas dalam Bidang Teknologi
Probabilitas memiliki peran penting dalam bidang teknologi, khususnya dalam pengembangan algoritma kecerdasan buatan, pemrosesan data, dan sistem keamanan.
- Kecerdasan Buatan: Probabilitas digunakan dalam pengembangan algoritma kecerdasan buatan, seperti dalam pembelajaran mesin dan pengenalan pola. Misalnya, algoritma kecerdasan buatan dapat menggunakan probabilitas untuk memprediksi perilaku pengguna atau mengenali objek dalam gambar.
- Pemrosesan Data: Probabilitas digunakan dalam pemrosesan data untuk mengidentifikasi pola, mengelola ketidakpastian, dan membuat prediksi. Misalnya, sistem pengenalan wajah dapat menggunakan probabilitas untuk menentukan kemungkinan kecocokan antara wajah yang dideteksi dengan database wajah.
- Sistem Keamanan: Probabilitas digunakan dalam pengembangan sistem keamanan, seperti sistem deteksi intrusi dan sistem otentikasi. Misalnya, sistem deteksi intrusi dapat menggunakan probabilitas untuk menilai kemungkinan serangan siber berdasarkan pola aktivitas jaringan.
Contoh Soal Statistika dan Penyelesaiannya
Statistika merupakan ilmu yang mempelajari cara mengumpulkan, mengolah, menganalisis, menginterpretasi, dan mempresentasikan data. Dalam kehidupan sehari-hari, statistika banyak diterapkan untuk berbagai keperluan, seperti penelitian, pengambilan keputusan, dan analisis data. Untuk memahami statistika, diperlukan latihan dalam menyelesaikan soal-soal statistika.
Contoh Soal Statistika tentang Pengumpulan Data
Pengumpulan data merupakan langkah awal dalam proses statistika. Data dapat dikumpulkan dari berbagai sumber, seperti observasi, wawancara, kuesioner, dan data sekunder. Berikut adalah contoh soal statistika tentang pengumpulan data:
- Seorang peneliti ingin mengetahui tingkat kepuasan pelanggan terhadap layanan di sebuah restoran. Bagaimana cara peneliti mengumpulkan data untuk menjawab pertanyaan tersebut?
Penyelesaian:
Peneliti dapat mengumpulkan data dengan cara:
- Melakukan survei dengan menyebarkan kuesioner kepada pelanggan yang berkunjung ke restoran.
- Melakukan wawancara langsung dengan pelanggan yang berkunjung ke restoran.
- Menganalisis data transaksi di restoran untuk mengetahui jumlah pelanggan yang kembali berkunjung.
Contoh Soal Statistika tentang Pengolahan Data
Setelah data dikumpulkan, data tersebut perlu diolah agar dapat dianalisis dan diinterpretasi. Pengolahan data meliputi berbagai kegiatan, seperti pengelompokan data, perhitungan statistik deskriptif, dan pembuatan tabel dan grafik.
- Seorang guru ingin mengetahui rata-rata nilai ulangan matematika siswa di kelasnya. Berikut adalah data nilai ulangan matematika siswa:
| Nama Siswa | Nilai |
|---|---|
| Andi | 80 |
| Budi | 75 |
| Candra | 85 |
| Dedi | 90 |
| Eka | 70 |
Berapakah rata-rata nilai ulangan matematika siswa di kelas tersebut?
Penyelesaian:
Rata-rata nilai ulangan matematika siswa di kelas tersebut dapat dihitung dengan rumus:
Rata-rata = Jumlah nilai / Jumlah siswa
Jumlah nilai = 80 + 75 + 85 + 90 + 70 = 400
Jumlah siswa = 5
Rata-rata = 400 / 5 = 80
Jadi, rata-rata nilai ulangan matematika siswa di kelas tersebut adalah 80.
Contoh soal probabilitas statistika dan penyelesaiannya bisa beragam, mulai dari menghitung peluang mendapatkan kartu As dalam satu set kartu remi hingga menghitung peluang seseorang terkena penyakit tertentu. Nah, bayangkan jika kita ingin menghitung peluang seseorang mengalami luka bakar akibat kecelakaan di rumah.
Nah, contoh soal luka bakar seperti ini bisa menjadi dasar untuk mempelajari probabilitas kejadian yang lebih kompleks, seperti menghitung probabilitas seseorang mengalami luka bakar berat akibat kecelakaan di rumah, atau menghitung probabilitas seseorang meninggal dunia akibat luka bakar. Dengan memahami probabilitas, kita bisa menganalisis risiko dan mengambil langkah pencegahan yang lebih tepat.
Contoh Soal Probabilitas dan Statistika Kombinasi
Contoh soal probabilitas dan statistika kombinasi biasanya menggabungkan konsep-konsep dari kedua bidang tersebut untuk menyelesaikan masalah yang lebih kompleks. Dalam soal ini, kita akan menganalisis suatu data dan menghitung probabilitas dari suatu kejadian berdasarkan data tersebut. Ini membantu kita untuk memahami hubungan antara probabilitas dan statistika dalam mengambil keputusan.
Contoh Soal Probabilitas dan Statistika Kombinasi
Misalnya, kita ingin mengetahui probabilitas seorang siswa mendapatkan nilai A dalam mata kuliah Statistika. Kita memiliki data nilai dari 100 siswa dalam mata kuliah tersebut. Data menunjukkan bahwa 20 siswa mendapatkan nilai A. Bagaimana kita menghitung probabilitas seorang siswa mendapatkan nilai A?
Langkah-langkah Penyelesaian Soal
- Menentukan Jumlah Sampel: Jumlah sampel dalam kasus ini adalah 100 siswa, karena kita memiliki data nilai dari 100 siswa.
- Menentukan Jumlah Kejadian: Jumlah kejadian yang kita cari adalah jumlah siswa yang mendapatkan nilai A, yaitu 20 siswa.
- Menghitung Probabilitas: Probabilitas seorang siswa mendapatkan nilai A dihitung dengan membagi jumlah kejadian (20 siswa) dengan jumlah sampel (100 siswa). Maka, probabilitasnya adalah 20/100 = 0,2 atau 20%.
Contoh Penyelesaian Soal
Dalam contoh soal di atas, kita telah menghitung probabilitas seorang siswa mendapatkan nilai A dalam mata kuliah Statistika. Kita dapat menggunakan probabilitas ini untuk membuat prediksi atau mengambil keputusan terkait dengan mata kuliah tersebut. Misalnya, kita dapat memperkirakan berapa banyak siswa yang akan mendapatkan nilai A pada semester berikutnya.
Kesalahan Umum dalam Menghitung Probabilitas
Menghitung probabilitas mungkin terlihat mudah, namun kesalahan umum seringkali muncul dalam penerapannya. Memahami kesalahan ini dan bagaimana menghindarinya sangat penting untuk memastikan analisis probabilitas yang akurat.
Mengabaikan Kejadian Saling Lepas
Kejadian saling lepas adalah kejadian yang tidak dapat terjadi bersamaan. Kesalahan umum adalah mengira bahwa kejadian saling lepas dapat terjadi bersamaan, sehingga probabilitasnya dijumlahkan secara langsung.
- Misalnya, jika kita melempar sebuah koin dua kali, kejadian mendapatkan sisi kepala pada lemparan pertama dan sisi kepala pada lemparan kedua adalah saling lepas. Probabilitas mendapatkan sisi kepala pada kedua lemparan bukanlah 1/2 + 1/2 = 1, melainkan 1/2 x 1/2 = 1/4.
Tidak Mempertimbangkan Semua Kemungkinan
Kesalahan umum lainnya adalah tidak mempertimbangkan semua kemungkinan hasil. Hal ini dapat terjadi ketika kita hanya fokus pada satu atau dua hasil yang paling jelas, tanpa memperhatikan hasil lainnya.
- Contohnya, jika kita memilih satu kartu secara acak dari satu set kartu remi, probabilitas mendapatkan kartu As adalah 4/52 = 1/13. Namun, jika kita hanya mempertimbangkan empat As tanpa mempertimbangkan 48 kartu lainnya, kita akan mendapatkan probabilitas yang salah.
Menggunakan Probabilitas Bersyarat Secara Salah
Probabilitas bersyarat adalah probabilitas suatu kejadian terjadi, dengan syarat kejadian lain telah terjadi. Kesalahan umum adalah menggunakan probabilitas bersyarat secara salah, mengira bahwa kejadian yang bersyarat tidak mempengaruhi probabilitas kejadian lainnya.
- Misalnya, jika kita memiliki dua kotak, kotak A berisi 2 bola merah dan 3 bola biru, sedangkan kotak B berisi 4 bola merah dan 1 bola biru. Kita mengambil satu kotak secara acak dan kemudian mengambil satu bola dari kotak tersebut. Probabilitas mengambil bola merah adalah 1/2 x 2/5 + 1/2 x 4/5 = 3/5. Namun, jika kita tahu bahwa kita telah mengambil kotak A, probabilitas mengambil bola merah menjadi 2/5.
Mengabaikan Ketergantungan
Kejadian yang saling tergantung adalah kejadian yang saling mempengaruhi. Kesalahan umum adalah mengira bahwa kejadian saling tergantung adalah saling lepas, sehingga probabilitasnya dikalikan secara langsung.
- Contohnya, jika kita mengambil dua kartu secara acak dari satu set kartu remi tanpa pengembalian, probabilitas mendapatkan kartu As pada pengambilan pertama dan kartu As pada pengambilan kedua adalah 4/52 x 3/51 = 1/221. Namun, jika kita mengira bahwa kedua kejadian ini saling lepas, kita akan mendapatkan probabilitas yang salah.
Mencampur Probabilitas dengan Frekuensi
Probabilitas adalah ukuran kemungkinan suatu kejadian terjadi, sedangkan frekuensi adalah jumlah kejadian yang terjadi dalam suatu periode waktu tertentu. Kesalahan umum adalah mencampur keduanya, mengira bahwa probabilitas sama dengan frekuensi.
- Misalnya, jika kita melempar koin 10 kali dan mendapatkan sisi kepala 6 kali, frekuensi sisi kepala adalah 6/10 = 0,6. Namun, probabilitas mendapatkan sisi kepala pada setiap lemparan adalah 1/2, bukan 0,6.
Kesimpulan Akhir
Dengan memahami konsep probabilitas dan statistika, Anda akan dapat mengambil keputusan yang lebih baik dan terinformasi dalam berbagai situasi. Mulai dari memprediksi hasil suatu eksperimen hingga menganalisis data untuk meningkatkan efisiensi suatu proses, pengetahuan ini akan membantu Anda melihat dunia dengan perspektif yang lebih luas.






