Contoh soal program dinamis dan penyelesaiannya – Pernahkah Anda merasa kesulitan dalam menentukan strategi terbaik untuk menyelesaikan masalah? Program dinamis hadir sebagai solusi cerdas untuk memecahkan masalah kompleks dengan mengurainya menjadi sub-masalah yang lebih kecil dan menggabungkan solusi optimalnya. Program dinamis sering dijumpai dalam kehidupan sehari-hari, seperti mencari rute terpendek untuk bepergian, mengalokasikan sumber daya secara efisien, atau bahkan menentukan strategi terbaik dalam permainan.
Dalam artikel ini, kita akan menjelajahi dunia program dinamis melalui contoh-contoh soal yang menarik dan langkah-langkah penyelesaiannya. Anda akan belajar tentang teknik top-down dan bottom-up, serta memahami bagaimana program dinamis dapat membantu Anda dalam mengoptimalkan solusi untuk berbagai masalah.
Pengertian Program Dinamis
Program dinamis adalah pendekatan untuk memecahkan masalah kompleks dengan membaginya menjadi sub-masalah yang lebih kecil dan kemudian menyelesaikan sub-masalah tersebut secara berulang. Solusi untuk setiap sub-masalah disimpan dalam tabel atau memori, sehingga dapat digunakan kembali untuk menyelesaikan sub-masalah yang lebih besar.
Contoh Sederhana Program Dinamis dalam Kehidupan Sehari-hari
Bayangkan Anda ingin mendaki gunung dengan jalur terpendek. Anda dapat memecah masalah ini menjadi sub-masalah yang lebih kecil, seperti menemukan jalur terpendek dari titik awal ke setiap titik di sepanjang jalur. Anda dapat menggunakan program dinamis untuk menghitung jalur terpendek dari titik awal ke setiap titik di sepanjang jalur, dan kemudian menggunakan informasi ini untuk menemukan jalur terpendek dari titik awal ke puncak gunung.
Prinsip Dasar Program Dinamis
- Prinsip Optimalitas: Solusi optimal untuk masalah dapat diperoleh dengan menggabungkan solusi optimal untuk sub-masalahnya.
- Substruktur Optimal: Solusi optimal untuk masalah dapat dibangun dari solusi optimal untuk sub-masalah yang lebih kecil.
- Memorization: Solusi untuk sub-masalah disimpan dalam tabel atau memori, sehingga dapat digunakan kembali untuk menyelesaikan sub-masalah yang lebih besar.
Konsep Dasar Program Dinamis
Program dinamis adalah teknik pemecahan masalah yang efektif untuk masalah-masalah yang memiliki struktur rekursif atau memiliki submasalah yang tumpang tindih. Dengan menggunakan pendekatan ini, kita dapat memecahkan masalah kompleks dengan memecahnya menjadi submasalah yang lebih kecil, menyelesaikan submasalah tersebut, dan kemudian menggabungkan solusi submasalah tersebut untuk mendapatkan solusi untuk masalah awal.
Karakteristik Masalah yang Cocok Diselesaikan dengan Program Dinamis
Program dinamis cocok digunakan untuk menyelesaikan masalah yang memiliki karakteristik tertentu. Berikut beberapa karakteristik tersebut:
- Optimal Substructure: Masalah dapat dipecah menjadi submasalah yang lebih kecil, dan solusi optimal untuk masalah awal dapat diperoleh dengan menggabungkan solusi optimal dari submasalah-submasalah tersebut.
- Overlapping Subproblems: Submasalah yang sama muncul berulang kali saat memecahkan masalah. Program dinamis menyimpan solusi untuk submasalah yang sudah dihitung, sehingga menghindari perhitungan berulang.
Konsep Subproblem dan Solusi Optimal dalam Program Dinamis
Program dinamis bergantung pada konsep subproblem dan solusi optimal.
- Subproblem: Submasalah adalah bagian kecil dari masalah utama yang dapat dipecahkan secara independen. Submasalah biasanya memiliki solusi optimal sendiri.
- Solusi Optimal: Solusi optimal untuk masalah utama diperoleh dengan menggabungkan solusi optimal dari semua submasalah.
Perbedaan Program Dinamis dengan Algoritma Greedy
Program dinamis dan algoritma greedy adalah teknik pemecahan masalah yang berbeda, meskipun keduanya mungkin tampak mirip pada awalnya. Perbedaan utama antara keduanya terletak pada cara mereka membuat keputusan.
- Program Dinamis: Membuat keputusan berdasarkan solusi optimal dari submasalah, yang dapat melibatkan perhitungan dan analisis yang lebih kompleks. Fokusnya adalah pada solusi optimal secara keseluruhan, meskipun mungkin membutuhkan waktu yang lebih lama untuk mencapai solusi tersebut.
- Algoritma Greedy: Membuat keputusan berdasarkan solusi yang tampaknya paling baik pada saat itu, tanpa mempertimbangkan dampak jangka panjang. Fokusnya adalah pada efisiensi waktu, tetapi solusi yang dihasilkan mungkin tidak selalu optimal.
Teknik Penyelesaian Program Dinamis: Contoh Soal Program Dinamis Dan Penyelesaiannya
Program dinamis adalah teknik yang digunakan untuk memecahkan masalah dengan memecahnya menjadi sub-masalah yang lebih kecil, dan kemudian menggabungkan solusi dari sub-masalah tersebut untuk mendapatkan solusi untuk masalah keseluruhan. Teknik ini sangat berguna untuk masalah yang memiliki sub-masalah yang saling tumpang tindih, sehingga solusi untuk satu sub-masalah dapat digunakan kembali untuk menyelesaikan sub-masalah lainnya.
Langkah-Langkah Umum dalam Program Dinamis
Langkah-langkah umum dalam menyelesaikan masalah dengan program dinamis adalah sebagai berikut:
- Identifikasi sub-masalah: Langkah pertama adalah mengidentifikasi sub-masalah yang lebih kecil yang dapat digunakan untuk menyelesaikan masalah utama. Sub-masalah harus saling tumpang tindih, sehingga solusi untuk satu sub-masalah dapat digunakan kembali untuk menyelesaikan sub-masalah lainnya.
- Buat tabel atau struktur data untuk menyimpan solusi sub-masalah: Setelah mengidentifikasi sub-masalah, Anda perlu membuat tabel atau struktur data untuk menyimpan solusi untuk setiap sub-masalah. Hal ini akan membantu Anda untuk menghindari perhitungan berulang.
- Selesaikan sub-masalah dalam urutan yang tepat: Anda perlu menyelesaikan sub-masalah dalam urutan yang tepat, sehingga solusi untuk satu sub-masalah dapat digunakan untuk menyelesaikan sub-masalah lainnya. Urutan yang tepat biasanya ditentukan oleh ketergantungan antara sub-masalah.
- Gunakan solusi sub-masalah untuk menyelesaikan masalah utama: Setelah menyelesaikan semua sub-masalah, Anda dapat menggunakan solusi sub-masalah untuk menyelesaikan masalah utama.
Perbedaan Teknik Top-Down dan Bottom-Up
Ada dua teknik utama dalam program dinamis: top-down dan bottom-up. Perbedaan utama antara kedua teknik ini adalah dalam cara mereka menyelesaikan sub-masalah.
| Teknik | Penjelasan |
|---|---|
| Top-Down (Memoization) | Teknik ini dimulai dengan menyelesaikan masalah utama dan kemudian secara rekursif memecahnya menjadi sub-masalah yang lebih kecil. Solusi untuk setiap sub-masalah disimpan dalam tabel atau struktur data, sehingga tidak perlu dihitung kembali jika diperlukan. |
| Bottom-Up (Tabulasi) | Teknik ini dimulai dengan menyelesaikan sub-masalah yang paling dasar dan kemudian secara bertahap membangun solusi untuk masalah yang lebih besar. Solusi untuk setiap sub-masalah disimpan dalam tabel atau struktur data, dan solusi untuk masalah yang lebih besar dihitung berdasarkan solusi sub-masalah sebelumnya. |
Contoh Penerapan Teknik Top-Down dan Bottom-Up
Berikut adalah contoh penerapan teknik top-down dan bottom-up dalam program dinamis:
Contoh Teknik Top-Down (Memoization)
Misalkan kita ingin mencari nilai Fibonacci ke-n. Kita dapat menggunakan teknik top-down dengan fungsi rekursif yang menyimpan solusi untuk setiap sub-masalah dalam tabel. Berikut adalah contoh implementasi dalam bahasa Python:
def fibonacci(n, memo=):
if n <= 1:
return n
if n in memo:
return memo[n]
memo[n] = fibonacci(n-1, memo) + fibonacci(n-2, memo)
return memo[n]
Fungsi ini menggunakan kamus memo untuk menyimpan solusi untuk setiap sub-masalah. Jika nilai Fibonacci ke-n sudah dihitung sebelumnya, fungsi tersebut langsung mengembalikan nilai dari kamus. Jika tidak, fungsi tersebut menghitung nilai Fibonacci ke-n secara rekursif dan menyimpan hasilnya dalam kamus.
Contoh Teknik Bottom-Up (Tabulasi)
Misalkan kita ingin mencari nilai Fibonacci ke-n. Kita dapat menggunakan teknik bottom-up dengan membuat tabel yang menyimpan nilai Fibonacci untuk setiap angka dari 0 hingga n. Berikut adalah contoh implementasi dalam bahasa Python:
def fibonacci(n):
table = [0] * (n + 1)
table[0] = 0
table[1] = 1
for i in range(2, n + 1):
table[i] = table[i-1] + table[i-2]
return table[n]
Fungsi ini membuat tabel yang menyimpan nilai Fibonacci untuk setiap angka dari 0 hingga n. Fungsi tersebut kemudian mengulangi setiap angka dari 2 hingga n dan menghitung nilai Fibonacci untuk angka tersebut berdasarkan nilai Fibonacci sebelumnya.
Contoh Soal Program Dinamis
Program dinamis adalah teknik pemecahan masalah yang efektif untuk masalah yang dapat dipecah menjadi sub-masalah yang lebih kecil. Teknik ini mengoptimalkan solusi dengan menyimpan hasil perhitungan sub-masalah sebelumnya untuk menghindari perhitungan berulang. Dalam contoh soal program dinamis ini, kita akan membahas tentang perhitungan nilai minimum atau maksimum.
Contoh Soal Program Dinamis: Perhitungan Nilai Minimum
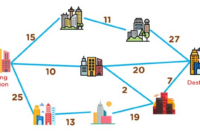
Bayangkan Anda ingin merencanakan perjalanan dari kota A ke kota D, dengan melewati kota B dan C. Anda memiliki beberapa pilihan jalur dengan biaya yang berbeda. Anda ingin menemukan jalur terpendek (dengan biaya minimum) untuk mencapai kota D.
Langkah-Langkah Penyelesaian dengan Teknik Bottom-Up
Berikut adalah langkah-langkah untuk menyelesaikan masalah ini dengan teknik bottom-up:
- Definisikan Sub-Masalah: Setiap kota (A, B, C, D) merupakan sub-masalah. Kita ingin mencari biaya minimum untuk mencapai setiap kota dari kota A.
- Menentukan Kasus Dasar: Biaya minimum untuk mencapai kota A adalah 0.
- Membangun Solusi dari Sub-Masalah: Kita akan menghitung biaya minimum untuk mencapai setiap kota dengan menggunakan informasi biaya minimum dari kota sebelumnya. Sebagai contoh, untuk mencapai kota B, kita perlu mempertimbangkan semua jalur dari kota A ke kota B dan memilih jalur dengan biaya minimum.
- Penyimpanan Hasil: Kita akan menyimpan hasil perhitungan biaya minimum untuk setiap kota dalam tabel. Tabel ini akan membantu kita menghindari perhitungan berulang.
Tabel Perhitungan Nilai Optimal
Berikut adalah tabel yang berisi perhitungan nilai optimal pada setiap tahap penyelesaian:
| Kota | Biaya Minimum dari Kota A |
|---|---|
| A | 0 |
| B | … (hitung biaya minimum dari jalur A ke B) |
| C | … (hitung biaya minimum dari jalur A ke C) |
| D | … (hitung biaya minimum dari jalur A ke D) |
Contoh Soal Program Dinamis: Perhitungan Nilai Maksimum
Contoh lainnya adalah perhitungan nilai maksimum dalam deret angka. Misalnya, Anda memiliki deret angka [1, 3, 2, 4, 5] dan ingin menemukan nilai maksimum dari sub-deret dengan panjang tertentu.
Langkah-Langkah Penyelesaian dengan Teknik Bottom-Up
Berikut adalah langkah-langkah untuk menyelesaikan masalah ini dengan teknik bottom-up:
- Definisikan Sub-Masalah: Setiap sub-deret dengan panjang tertentu (misalnya, sub-deret dengan panjang 2, 3, dan seterusnya) merupakan sub-masalah.
- Menentukan Kasus Dasar: Nilai maksimum dari sub-deret dengan panjang 1 adalah angka pertama dalam deret.
- Membangun Solusi dari Sub-Masalah: Kita akan menghitung nilai maksimum dari setiap sub-deret dengan menggunakan informasi nilai maksimum dari sub-deret sebelumnya. Sebagai contoh, untuk menghitung nilai maksimum dari sub-deret dengan panjang 2, kita perlu mempertimbangkan nilai maksimum dari sub-deret dengan panjang 1 dan menambahkan angka kedua dalam deret.
- Penyimpanan Hasil: Kita akan menyimpan hasil perhitungan nilai maksimum untuk setiap sub-deret dalam tabel. Tabel ini akan membantu kita menghindari perhitungan berulang.
Tabel Perhitungan Nilai Optimal
Berikut adalah tabel yang berisi perhitungan nilai optimal pada setiap tahap penyelesaian:
| Panjang Sub-Deret | Nilai Maksimum |
|---|---|
| 1 | 1 |
| 2 | … (hitung nilai maksimum dari sub-deret dengan panjang 2) |
| 3 | … (hitung nilai maksimum dari sub-deret dengan panjang 3) |
| … | … |
Contoh Soal Program Dinamis (Lanjutan)
Program dinamis merupakan teknik yang efektif untuk menyelesaikan masalah optimasi dengan memecah masalah menjadi sub-masalah yang lebih kecil dan menyimpan solusi sub-masalah tersebut untuk menghindari perhitungan berulang. Dalam contoh soal program dinamis sebelumnya, kita telah membahas masalah penjumlahan maksimum dan pencarian jalur terpendek. Sekarang, kita akan membahas contoh soal yang melibatkan penentuan urutan optimal.
Contoh Soal: Penjadwalan Tugas
Misalkan kita memiliki sejumlah tugas yang perlu diselesaikan. Setiap tugas memiliki durasi tertentu dan deadline. Tujuannya adalah untuk menemukan urutan tugas yang optimal yang meminimalkan total waktu terlambat.
Penyelesaian dengan Teknik Top-Down
Teknik top-down dalam program dinamis melibatkan pemecahan masalah secara rekursif dengan memecah masalah menjadi sub-masalah yang lebih kecil dan menyimpan solusi sub-masalah tersebut dalam tabel. Berikut langkah-langkah penyelesaian contoh soal penjadwalan tugas menggunakan teknik top-down:
- Definisikan sub-masalah: Sub-masalah dalam kasus ini adalah menentukan urutan tugas optimal untuk subset tugas yang diberikan. Kita dapat mendefinisikan sub-masalah sebagai berikut:
- T[i, j]: Waktu terlambat minimum untuk menyelesaikan tugas dari 1 hingga i dengan deadline j.
- Tentukan kasus dasar: Kasus dasar adalah ketika kita hanya memiliki satu tugas atau tidak ada tugas sama sekali. Dalam kasus ini, waktu terlambat minimum adalah 0.
- T[0, j] = 0 (tidak ada tugas)
- T[i, 0] = 0 (tidak ada deadline)
- Rekursi: Untuk menyelesaikan sub-masalah T[i, j], kita dapat mempertimbangkan dua kemungkinan:
- Tidak menyertakan tugas ke-i: Dalam kasus ini, waktu terlambat minimum sama dengan waktu terlambat minimum untuk menyelesaikan tugas dari 1 hingga i-1 dengan deadline j. Yaitu, T[i, j] = T[i-1, j].
- Menyertakan tugas ke-i: Dalam kasus ini, kita perlu menghitung waktu terlambat untuk tugas ke-i dan menambahkannya ke waktu terlambat minimum untuk menyelesaikan tugas dari 1 hingga i-1 dengan deadline j-durasi tugas ke-i. Yaitu, T[i, j] = T[i-1, j-durasi tugas ke-i] + waktu terlambat tugas ke-i.
- Menghitung solusi optimal: Untuk menemukan solusi optimal, kita perlu menghitung nilai T[n, d] di mana n adalah jumlah tugas dan d adalah deadline keseluruhan.
Tabel Perhitungan, Contoh soal program dinamis dan penyelesaiannya
Berikut tabel yang berisi perhitungan nilai optimal pada setiap tahap penyelesaian. Misalkan kita memiliki 3 tugas dengan durasi dan deadline sebagai berikut:
| Tugas | Durasi | Deadline |
|---|---|---|
| 1 | 2 | 4 |
| 2 | 1 | 3 |
| 3 | 3 | 5 |
Tabel berikut menunjukkan perhitungan nilai T[i, j] untuk setiap kombinasi i dan j:
| i\j | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 1 | 1 | 1 |
| 3 | 0 | 0 | 0 | 1 | 1 | 3 |
Berdasarkan tabel, waktu terlambat minimum untuk menyelesaikan ketiga tugas dengan deadline 5 adalah 3. Urutan tugas optimal yang menghasilkan waktu terlambat minimum adalah tugas 2, kemudian tugas 1, dan terakhir tugas 3.
Contoh Soal Program Dinamis (Perhitungan Nilai Minimum)
Program dinamis adalah teknik pemecahan masalah dengan membagi masalah besar menjadi sub-masalah yang lebih kecil, kemudian menyelesaikan sub-masalah tersebut secara berulang dan menyimpan solusinya. Setelah itu, solusi dari sub-masalah digabungkan untuk mendapatkan solusi dari masalah utama. Program dinamis sangat efektif untuk menyelesaikan masalah yang melibatkan optimasi, seperti menemukan nilai minimum atau maksimum.
Salah satu contoh penerapan program dinamis adalah dalam perhitungan nilai minimum biaya. Dalam contoh ini, kita akan mencoba menentukan jalur dengan biaya minimum untuk mencapai titik tujuan tertentu.
Contoh Soal Perhitungan Nilai Minimum Biaya
Misalkan kita memiliki sebuah peta dengan beberapa titik yang terhubung dengan jalur. Setiap jalur memiliki biaya tertentu. Kita ingin menemukan jalur dengan biaya minimum dari titik awal (A) ke titik tujuan (F). Berikut adalah contoh peta dan biaya jalur:
Contoh Peta dan Biaya Jalur:
| Jalur | Biaya |
|---|---|
| A – B | 2 |
| A – C | 3 |
| B – D | 1 |
| B – E | 4 |
| C – D | 2 |
| C – E | 5 |
| D – F | 3 |
| E – F | 2 |
Untuk menemukan jalur dengan biaya minimum, kita dapat menggunakan teknik program dinamis dengan pendekatan bottom-up. Berikut adalah langkah-langkahnya:
Langkah-Langkah Penyelesaian dengan Teknik Bottom-Up
- Inisialisasi Tabel: Buat tabel yang berisi semua titik dan biaya minimum untuk mencapai titik tersebut dari titik awal (A). Tabel ini akan digunakan untuk menyimpan hasil perhitungan biaya minimum.
- Perhitungan Biaya Minimum: Mulai dari titik awal (A), hitung biaya minimum untuk mencapai setiap titik lainnya. Untuk setiap titik, periksa semua jalur yang terhubung ke titik tersebut dan hitung biaya total untuk mencapai titik tersebut melalui jalur tersebut. Pilih jalur dengan biaya total minimum dan catat biaya minimum tersebut di tabel.
- Rekursi: Ulangi langkah 2 untuk setiap titik hingga mencapai titik tujuan (F).
- Menentukan Jalur Minimum: Setelah tabel diisi, jalur dengan biaya minimum dapat ditentukan dengan melacak jalur dengan biaya minimum dari titik awal (A) ke titik tujuan (F).
Tabel Perhitungan Nilai Minimum Biaya
Berikut adalah tabel yang berisi perhitungan nilai minimum biaya pada setiap tahap penyelesaian:
| Titik | Biaya Minimum | Jalur |
|---|---|---|
| A | 0 | – |
| B | 2 | A – B |
| C | 3 | A – C |
| D | 3 | A – B – D |
| E | 6 | A – B – E |
| F | 6 | A – B – D – F |
Dari tabel tersebut, kita dapat melihat bahwa biaya minimum untuk mencapai titik F dari titik A adalah 6. Jalur dengan biaya minimum adalah A – B – D – F.
Contoh Soal Program Dinamis (Penentuan Urutan Optimal)
Program dinamis adalah teknik pemecahan masalah yang memecah masalah kompleks menjadi sub-masalah yang lebih kecil, menyelesaikan sub-masalah secara rekursif, dan menyimpan hasil perhitungan untuk menghindari perhitungan berulang. Teknik ini sangat efektif dalam menyelesaikan masalah yang melibatkan penentuan urutan optimal, seperti penjadwalan pekerjaan, penentuan jalur terpendek, atau penentuan strategi permainan.
Dalam contoh soal ini, kita akan membahas bagaimana program dinamis dapat digunakan untuk menentukan urutan optimal pekerjaan. Misalkan kita memiliki serangkaian pekerjaan dengan waktu penyelesaian tertentu dan ketergantungan antara pekerjaan tersebut. Kita ingin menemukan urutan pekerjaan yang meminimalkan total waktu penyelesaian.
Contoh Soal
Misalkan kita memiliki 5 pekerjaan dengan waktu penyelesaian dan ketergantungan sebagai berikut:
| Pekerjaan | Waktu Penyelesaian | Ketergantungan |
|---|---|---|
| A | 2 | – |
| B | 3 | A |
| C | 1 | A |
| D | 4 | B, C |
| E | 2 | D |
Tujuan kita adalah untuk menentukan urutan pekerjaan yang meminimalkan total waktu penyelesaian. Misalnya, urutan pekerjaan A, C, B, D, E memiliki total waktu penyelesaian 2 + 1 + 3 + 4 + 2 = 12.
Penyelesaian dengan Teknik Top-Down
Teknik top-down adalah pendekatan yang memecah masalah menjadi sub-masalah yang lebih kecil, menyelesaikan sub-masalah secara rekursif, dan menyimpan hasil perhitungan untuk menghindari perhitungan berulang. Berikut adalah langkah-langkah penyelesaian contoh soal program dinamis menggunakan teknik top-down:
- Definisi Sub-Masalah: Sub-masalah dalam kasus ini adalah menentukan urutan optimal untuk menyelesaikan pekerjaan dari 1 hingga i, di mana i adalah indeks pekerjaan.
- Rekursi: Kita dapat menyelesaikan sub-masalah dengan rekursi. Misalkan, untuk menentukan urutan optimal pekerjaan dari 1 hingga i, kita perlu mempertimbangkan semua pekerjaan yang dapat dilakukan sebelum pekerjaan i, dan memilih urutan yang meminimalkan total waktu penyelesaian. Jika pekerjaan j adalah pekerjaan terakhir yang dilakukan sebelum pekerjaan i, maka total waktu penyelesaian untuk menyelesaikan pekerjaan dari 1 hingga i adalah total waktu penyelesaian untuk menyelesaikan pekerjaan dari 1 hingga j ditambah waktu penyelesaian pekerjaan i.
- Memorization: Untuk menghindari perhitungan berulang, kita dapat menyimpan hasil perhitungan untuk setiap sub-masalah. Ini dapat dilakukan dengan menggunakan tabel yang berisi total waktu penyelesaian optimal untuk setiap sub-masalah.
Tabel Perhitungan Nilai Optimal
Tabel berikut menunjukkan perhitungan nilai optimal untuk setiap sub-masalah:
| Pekerjaan (i) | Total Waktu Penyelesaian Optimal | Urutan Optimal |
|---|---|---|
| 1 (A) | 2 | A |
| 2 (B) | 5 | A, B |
| 3 (C) | 3 | A, C |
| 4 (D) | 9 | A, C, B, D |
| 5 (E) | 11 | A, C, B, D, E |
Dari tabel di atas, kita dapat melihat bahwa urutan optimal untuk menyelesaikan pekerjaan dari 1 hingga 5 adalah A, C, B, D, E dengan total waktu penyelesaian optimal 11.
Implementasi Program Dinamis
Program dinamis adalah teknik pemecahan masalah yang memecah masalah besar menjadi sub-masalah yang lebih kecil, menyelesaikan sub-masalah tersebut, dan menyimpan solusinya untuk digunakan kembali ketika dihadapkan pada sub-masalah yang sama. Teknik ini sangat efektif untuk menyelesaikan masalah yang memiliki sub-struktur optimal dan solusi optimal untuk sub-masalah dapat digunakan untuk menemukan solusi optimal untuk masalah yang lebih besar.
Berikut ini adalah contoh kode program dalam bahasa Python untuk menyelesaikan masalah Fibonacci dengan menggunakan program dinamis.
Contoh Kode Program
Berikut adalah kode program Python yang mengimplementasikan program dinamis untuk menyelesaikan masalah Fibonacci:
def fibonacci(n):
"""
Fungsi untuk menghitung deret Fibonacci menggunakan program dinamis.
Args:
n: Integer yang menunjukkan jumlah elemen deret Fibonacci yang ingin dihitung.
Returns:
Integer yang menunjukkan elemen ke-n dari deret Fibonacci.
"""
if n <= 1:
return n
else:
dp = [0] * (n + 1)
dp[0] = 0
dp[1] = 1
for i in range(2, n + 1):
dp[i] = dp[i - 1] + dp[i - 2]
return dp[n]
# Contoh penggunaan fungsi
n = 10
result = fibonacci(n)
print(f"Elemen ke-n dari deret Fibonacci adalah: result")
Kode program di atas mendefinisikan fungsi fibonacci(n) yang mengambil integer n sebagai input dan mengembalikan elemen ke-n dari deret Fibonacci. Fungsi ini menggunakan array dp untuk menyimpan hasil perhitungan elemen Fibonacci sebelumnya. Array ini diinisialisasi dengan 0 untuk elemen pertama dan 1 untuk elemen kedua. Kemudian, loop for digunakan untuk menghitung elemen Fibonacci berikutnya dengan menjumlahkan dua elemen sebelumnya. Hasil perhitungan disimpan di array dp. Akhirnya, fungsi mengembalikan elemen ke-n dari array dp.
Dalam contoh penggunaan fungsi, kita menetapkan n ke 10 dan memanggil fungsi fibonacci(n). Hasilnya disimpan di variabel result dan dicetak ke layar. Output dari kode program ini adalah:
Elemen ke-10 dari deret Fibonacci adalah: 55
Contoh Soal Program Dinamis (Pencarian String)
Program dinamis adalah teknik pemecahan masalah yang memecah masalah besar menjadi sub-masalah yang lebih kecil, menyelesaikan sub-masalah, dan menyimpan solusinya untuk digunakan kembali saat memecahkan masalah yang lebih besar. Teknik ini sangat berguna dalam masalah yang melibatkan pencarian pola string dalam teks.
Contoh Soal Program Dinamis (Pencarian String)
Misalkan kita memiliki teks “bananas” dan pola “ana”. Kita ingin mencari tahu apakah pola tersebut terdapat dalam teks dan jika ya, di mana letaknya.
Penyelesaian dengan Teknik Bottom-Up
Berikut langkah-langkah penyelesaian contoh soal program dinamis tersebut menggunakan teknik bottom-up:
- Buat tabel dengan ukuran (panjang teks + 1) x (panjang pola + 1). Tabel ini akan menyimpan informasi tentang kecocokan pola dalam teks.
- Inisialisasi baris dan kolom pertama tabel dengan nilai 0. Ini menunjukkan bahwa tidak ada kecocokan pola pada indeks 0 dari teks atau pola.
- Iterasi melalui setiap karakter dalam teks dan setiap karakter dalam pola. Untuk setiap pasangan karakter, periksa apakah karakter tersebut cocok. Jika cocok, maka nilai pada tabel untuk indeks tersebut adalah nilai pada tabel untuk indeks sebelumnya ditambah 1. Jika tidak cocok, maka nilai pada tabel untuk indeks tersebut adalah 0.
- Setelah iterasi selesai, nilai pada tabel akan menunjukkan kecocokan pola dalam teks. Jika nilai pada tabel untuk indeks terakhir dari teks dan pola lebih besar dari 0, maka pola terdapat dalam teks.
Tabel Perhitungan Nilai Optimal
Berikut adalah tabel yang berisi perhitungan nilai optimal pada setiap tahap penyelesaian:
| a | n | a | ||
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| b | 0 | 0 | 0 | 0 |
| a | 0 | 1 | 0 | 1 |
| n | 0 | 0 | 1 | 0 |
| a | 0 | 1 | 0 | 2 |
| n | 0 | 0 | 1 | 0 |
| a | 0 | 1 | 0 | 2 |
| s | 0 | 0 | 0 | 0 |
Dari tabel tersebut, kita dapat melihat bahwa nilai pada tabel untuk indeks terakhir dari teks dan pola adalah 2. Ini menunjukkan bahwa pola “ana” terdapat dalam teks “bananas” dan letaknya pada indeks 1 hingga 3.
Contoh Soal Program Dinamis (Knapsack Problem)
Program dinamis merupakan teknik yang efektif untuk menyelesaikan masalah optimisasi dengan memecahnya menjadi sub-masalah yang lebih kecil dan saling berhubungan. Salah satu contoh klasik masalah program dinamis adalah Knapsack Problem, di mana kita diberikan sebuah ransel dengan kapasitas terbatas dan sejumlah barang dengan nilai dan berat masing-masing. Tujuannya adalah untuk memilih kombinasi barang yang dapat dimasukkan ke dalam ransel sehingga total nilai barang yang dipilih maksimal, tanpa melebihi kapasitas ransel.
Contoh Soal Knapsack Problem
Misalkan kita memiliki sebuah ransel dengan kapasitas 5 kg. Tersedia 4 barang dengan nilai dan berat sebagai berikut:
| Barang | Nilai (Rp) | Berat (kg) |
|---|---|---|
| 1 | 60 | 2 |
| 2 | 100 | 3 |
| 3 | 120 | 4 |
| 4 | 50 | 1 |
Tentukan kombinasi barang yang dapat dimasukkan ke dalam ransel sehingga total nilai barang yang dipilih maksimal, tanpa melebihi kapasitas ransel.
Penyelesaian dengan Teknik Top-Down
Teknik top-down dalam program dinamis melibatkan rekursi dan memoisasi untuk menghindari perhitungan yang berulang. Berikut adalah langkah-langkah penyelesaian contoh soal knapsack problem menggunakan teknik top-down:
- Definisikan Sub-masalah: Sub-masalah dalam kasus ini adalah menentukan nilai optimal untuk memilih barang dari i barang pertama dengan kapasitas j. Kita dapat mendefinisikan fungsi rekursif
knapsack(i, j)untuk mewakili sub-masalah ini. - Kasus Dasar: Kasus dasar adalah ketika i = 0 (tidak ada barang) atau j = 0 (kapasitas ransel 0). Dalam kasus ini, nilai optimal adalah 0.
- Rekursi: Untuk kasus i > 0 dan j > 0, kita memiliki dua pilihan:
- Tidak Memilih Barang ke-i: Dalam kasus ini, nilai optimal adalah sama dengan nilai optimal untuk memilih dari i – 1 barang pertama dengan kapasitas j, yaitu
knapsack(i - 1, j). - Memilih Barang ke-i: Dalam kasus ini, nilai optimal adalah nilai barang ke-i ditambah nilai optimal untuk memilih dari i – 1 barang pertama dengan kapasitas j dikurangi berat barang ke-i, yaitu
nilai[i] + knapsack(i - 1, j - berat[i]).
Nilai optimal untuk sub-masalah
knapsack(i, j)adalah maksimum dari kedua pilihan tersebut. - Tidak Memilih Barang ke-i: Dalam kasus ini, nilai optimal adalah sama dengan nilai optimal untuk memilih dari i – 1 barang pertama dengan kapasitas j, yaitu
- Memoisasi: Untuk menghindari perhitungan yang berulang, kita dapat menyimpan hasil perhitungan untuk setiap sub-masalah dalam sebuah tabel. Tabel ini akan berisi nilai optimal untuk setiap kombinasi i dan j.
Tabel Perhitungan Nilai Optimal
Tabel berikut menunjukkan perhitungan nilai optimal pada setiap tahap penyelesaian:
| j = 0 | j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | |
|---|---|---|---|---|---|---|
| i = 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i = 1 | 0 | 50 | 60 | 60 | 60 | 60 |
| i = 2 | 0 | 50 | 60 | 100 | 110 | 160 |
| i = 3 | 0 | 50 | 60 | 100 | 120 | 160 |
| i = 4 | 0 | 50 | 60 | 100 | 120 | 170 |
Berdasarkan tabel, nilai optimal untuk memilih dari 4 barang pertama dengan kapasitas 5 kg adalah 170. Kombinasi barang yang dipilih adalah barang 1, 2, dan 4 dengan total nilai 170 dan total berat 5 kg.
Contoh soal program dinamis dan penyelesaiannya bisa ditemukan di berbagai bidang, seperti pada masalah optimasi jalur terpendek atau penjadwalan. Salah satu contoh menarik adalah soal pelayangan bunyi, seperti yang dibahas di contoh soal pelayangan bunyi. Di sini, kita bisa menggunakan program dinamis untuk menentukan jalur pelayangan bunyi yang paling efisien dengan mempertimbangkan faktor-faktor seperti kecepatan angin dan arah.
Penerapan program dinamis dalam berbagai kasus seperti ini menunjukkan betapa pentingnya memahami konsep ini dalam memecahkan masalah kompleks.
Aplikasi Program Dinamis
Program dinamis adalah teknik pemecahan masalah yang memecah masalah kompleks menjadi sub-masalah yang lebih kecil, menyelesaikan sub-masalah tersebut, dan kemudian menggabungkan solusi tersebut untuk mendapatkan solusi untuk masalah asli. Teknik ini sangat efektif dalam menyelesaikan masalah yang memiliki sub-masalah yang saling tumpang tindih, karena memungkinkan untuk menghitung solusi untuk setiap sub-masalah hanya sekali dan menyimpan hasilnya untuk digunakan kembali saat dibutuhkan.
Algoritma Pencarian
Program dinamis dapat diterapkan dalam algoritma pencarian untuk menemukan jalur terpendek atau solusi optimal untuk masalah tertentu. Salah satu contohnya adalah algoritma Dijkstra, yang digunakan untuk menemukan jalur terpendek antara dua titik dalam grafik. Algoritma ini menggunakan program dinamis untuk menghitung jarak terpendek dari titik awal ke semua titik lain dalam grafik, dengan menyimpan jarak terpendek yang ditemukan sejauh ini untuk setiap titik. Dengan menyimpan hasil perhitungan ini, algoritma dapat menghindari perhitungan ulang jarak yang sama berulang kali, sehingga meningkatkan efisiensi pencarian.
Kompresi Data
Program dinamis juga dapat digunakan dalam kompresi data untuk mengurangi ukuran file data tanpa kehilangan informasi yang signifikan. Salah satu teknik kompresi data yang menggunakan program dinamis adalah algoritma Lempel-Ziv (LZ77). Algoritma ini bekerja dengan mencari pola berulang dalam data dan menggantinya dengan referensi ke pola sebelumnya. Program dinamis digunakan untuk mencari pola berulang yang paling efisien, dengan menyimpan hasil pencarian untuk digunakan kembali dalam proses kompresi.
Pemrosesan Gambar
Dalam pemrosesan gambar, program dinamis dapat digunakan untuk berbagai tugas, seperti segmentasi gambar, pengenalan pola, dan pengolahan citra. Misalnya, dalam segmentasi gambar, program dinamis dapat digunakan untuk menemukan batas objek dalam gambar dengan meminimalkan biaya total untuk memisahkan objek dari latar belakang. Teknik ini menggunakan program dinamis untuk menghitung biaya minimum untuk memisahkan setiap piksel dalam gambar ke dalam objek atau latar belakang, dengan menyimpan hasil perhitungan untuk setiap piksel.
Penutupan
Memahami program dinamis membuka pintu bagi kita untuk berpikir secara strategis dan mengoptimalkan solusi dalam berbagai bidang. Dengan menguraikan masalah kompleks menjadi sub-masalah yang lebih kecil, program dinamis memungkinkan kita untuk menemukan solusi optimal dengan efisien. Mari kita terus belajar dan menjelajahi berbagai aplikasi program dinamis yang bermanfaat dalam kehidupan sehari-hari.