Contoh soal program linear dan jawabannya – Program linear, sebuah cabang matematika yang menarik, membantu kita dalam menemukan solusi optimal untuk masalah yang melibatkan sumber daya terbatas. Bayangkan Anda memiliki toko kue dan ingin memaksimalkan keuntungan dengan memproduksi dua jenis kue: cokelat dan vanila. Setiap kue membutuhkan bahan baku yang berbeda dan waktu produksi yang berbeda pula. Bagaimana Anda menentukan jumlah kue yang harus diproduksi untuk mendapatkan keuntungan maksimal? Di sinilah program linear berperan!
Program linear menyediakan kerangka kerja untuk memodelkan masalah seperti ini, dengan menggunakan persamaan dan pertidaksamaan matematika. Dengan menggunakan model matematika, kita dapat menemukan solusi optimal yang akan memaksimalkan keuntungan atau meminimalkan biaya, dengan mempertimbangkan kendala-kendala yang ada.
Pengertian Program Linear
Program linear adalah metode matematika yang digunakan untuk mencari solusi optimal untuk masalah yang melibatkan pembatasan dan tujuan yang dinyatakan dalam bentuk persamaan atau pertidaksamaan linear. Program linear membantu kita dalam menentukan cara terbaik untuk mengalokasikan sumber daya yang terbatas untuk mencapai hasil yang diinginkan.
Konsep Dasar Program Linear
Program linear didasarkan pada konsep-konsep matematika seperti persamaan dan pertidaksamaan linear, fungsi objektif, dan kendala.
- Persamaan dan Pertidaksamaan Linear: Persamaan linear adalah persamaan yang menyatakan hubungan linear antara variabel. Pertidaksamaan linear adalah pernyataan yang membandingkan dua ekspresi linear dengan tanda “lebih besar dari”, “lebih kecil dari”, “lebih besar dari atau sama dengan”, atau “lebih kecil dari atau sama dengan”.
- Fungsi Objektif: Fungsi objektif adalah fungsi yang menyatakan tujuan yang ingin dicapai dalam masalah program linear. Fungsi objektif biasanya berupa persamaan linear yang ingin dimaksimalkan atau diminimalkan.
- Kendala: Kendala adalah batasan atau syarat yang harus dipenuhi dalam masalah program linear. Kendala biasanya dinyatakan dalam bentuk pertidaksamaan linear yang menunjukkan batasan sumber daya atau faktor lainnya.
Contoh Permasalahan Sehari-hari
Misalnya, seorang pengusaha kue ingin menentukan jumlah kue cokelat dan kue vanila yang harus dibuat setiap hari untuk memaksimalkan keuntungannya. Dia memiliki 10 kg tepung dan 5 kg gula yang tersedia. Kue cokelat membutuhkan 2 kg tepung dan 1 kg gula, sedangkan kue vanila membutuhkan 1 kg tepung dan 2 kg gula. Setiap kue cokelat menghasilkan keuntungan Rp 5.000, sedangkan kue vanila menghasilkan keuntungan Rp 4.000.
Perbedaan Program Linear dan Program Non-linear
Berikut tabel yang membandingkan program linear dengan program non-linear:
| Karakteristik | Program Linear | Program Non-linear |
|---|---|---|
| Fungsi Objektif | Linear | Non-linear |
| Kendala | Linear | Non-linear |
| Solusi Optimal | Titik sudut pada daerah feasible | Titik optimum dapat berada di titik sudut atau di dalam daerah feasible |
| Metode Solusi | Metode Simplex, Metode Grafik | Metode numerik, Metode Lagrange |
Model Matematika Program Linear
Program linear merupakan suatu metode optimasi yang digunakan untuk menentukan nilai optimal dari suatu fungsi tujuan yang dibatasi oleh beberapa kendala linear. Model matematika program linear merupakan representasi matematis dari suatu masalah program linear. Model ini terdiri dari tiga komponen utama, yaitu variabel keputusan, fungsi tujuan, dan kendala.
Langkah-Langkah Merumuskan Model Matematika Program Linear
Merumuskan model matematika program linear membutuhkan beberapa langkah yang terstruktur untuk memastikan representasi masalah yang akurat. Berikut adalah langkah-langkahnya:
- Identifikasi variabel keputusan: Variabel keputusan adalah variabel yang dapat dikendalikan dan akan memengaruhi hasil optimal. Variabel ini biasanya dilambangkan dengan huruf-huruf seperti x, y, z, dan seterusnya.
- Tentukan fungsi tujuan: Fungsi tujuan adalah fungsi matematis yang ingin dimaksimalkan atau diminimalkan. Fungsi ini menyatakan hubungan antara variabel keputusan dan nilai yang ingin dicapai.
- Tentukan kendala: Kendala adalah batasan yang membatasi nilai variabel keputusan. Kendala ini biasanya berupa persamaan atau pertidaksamaan linear.
- Tuliskan model matematika: Setelah mengidentifikasi variabel keputusan, fungsi tujuan, dan kendala, model matematika program linear dapat dituliskan dalam bentuk persamaan atau pertidaksamaan linear.
Contoh Soal Program Linear dan Model Matematikanya
Berikut adalah contoh soal program linear dan model matematikanya:
Sebuah perusahaan memproduksi dua jenis produk, yaitu produk A dan produk B. Setiap produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku, sedangkan setiap produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku. Perusahaan memiliki 10 jam waktu produksi dan 8 kg bahan baku yang tersedia. Keuntungan per unit produk A adalah Rp. 10.000,- dan keuntungan per unit produk B adalah Rp. 15.000,-. Berapakah jumlah masing-masing produk yang harus diproduksi untuk memaksimalkan keuntungan?
Berikut adalah model matematika program linear untuk soal tersebut:
Variabel keputusan:
- x = jumlah produk A yang diproduksi
- y = jumlah produk B yang diproduksi
Fungsi tujuan:
- Maksimumkan keuntungan = 10.000x + 15.000y
Kendala:
- 2x + y ≤ 10 (kendala waktu produksi)
- x + 2y ≤ 8 (kendala bahan baku)
- x ≥ 0 (jumlah produk A tidak boleh negatif)
- y ≥ 0 (jumlah produk B tidak boleh negatif)
Model matematika:
- Maksimumkan Z = 10.000x + 15.000y
- 2x + y ≤ 10
- x + 2y ≤ 8
- x ≥ 0
- y ≥ 0
Identifikasi Variabel Keputusan, Fungsi Tujuan, dan Kendala dalam Model Matematika Program Linear
Dalam model matematika program linear, penting untuk mengidentifikasi komponen-komponennya dengan jelas.
- Variabel keputusan: Variabel keputusan adalah variabel yang dapat dikendalikan dan akan memengaruhi hasil optimal. Dalam contoh soal di atas, variabel keputusan adalah x (jumlah produk A) dan y (jumlah produk B).
- Fungsi tujuan: Fungsi tujuan adalah fungsi matematis yang ingin dimaksimalkan atau diminimalkan. Dalam contoh soal di atas, fungsi tujuan adalah Maksimumkan Z = 10.000x + 15.000y, yang menyatakan bahwa tujuannya adalah untuk memaksimalkan keuntungan.
- Kendala: Kendala adalah batasan yang membatasi nilai variabel keputusan. Dalam contoh soal di atas, kendala adalah 2x + y ≤ 10, x + 2y ≤ 8, x ≥ 0, dan y ≥ 0. Kendala ini menyatakan bahwa jumlah waktu produksi dan bahan baku yang digunakan tidak boleh melebihi ketersediaan yang ada, dan jumlah produk tidak boleh negatif.
Metode Grafik
Metode grafik adalah salah satu cara untuk menyelesaikan program linear. Metode ini memanfaatkan representasi visual dari kendala dan fungsi tujuan dalam bentuk grafik. Dengan menggunakan grafik, kita dapat menentukan area solusi yang memenuhi semua kendala dan kemudian mencari titik optimum yang memaksimalkan atau meminimalkan fungsi tujuan.
Cara Menyelesaikan Program Linear dengan Metode Grafik
Metode grafik melibatkan beberapa langkah penting untuk menyelesaikan program linear. Berikut langkah-langkahnya:
- Ubah setiap kendala dalam bentuk persamaan linear.
- Gambar garis yang mewakili setiap persamaan linear pada grafik.
- Tentukan area solusi yang memenuhi semua kendala. Area solusi adalah wilayah yang terletak di sisi garis yang benar untuk setiap kendala.
- Tentukan titik-titik sudut dari area solusi. Titik-titik sudut adalah titik-titik yang berada di perpotongan antara garis-garis kendala.
- Hitung nilai fungsi tujuan pada setiap titik sudut.
- Tentukan titik optimum yang memaksimalkan atau meminimalkan fungsi tujuan, tergantung pada tujuan program linear.
Contoh Soal Program Linear dan Penyelesaian dengan Metode Grafik
Sebuah perusahaan memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku, sedangkan produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku. Perusahaan memiliki 10 jam waktu produksi dan 8 kg bahan baku yang tersedia. Keuntungan untuk setiap unit produk A adalah Rp 10.000 dan untuk produk B adalah Rp 15.000. Tentukan jumlah produksi masing-masing produk yang memaksimalkan keuntungan perusahaan.
Penyelesaian:
1. Menetapkan variabel:
* Misalkan x adalah jumlah produk A yang diproduksi.
* Misalkan y adalah jumlah produk B yang diproduksi.
2. Membuat fungsi tujuan:
* Keuntungan total = 10.000x + 15.000y
3. Membuat kendala:
* Kendala waktu produksi: 2x + y ≤ 10
* Kendala bahan baku: x + 2y ≤ 8
* Kendala non-negatif: x ≥ 0, y ≥ 0
4. Menggambar grafik:
* Gambar garis 2x + y = 10 dengan menggambar dua titik (0, 10) dan (5, 0).
* Gambar garis x + 2y = 8 dengan menggambar dua titik (0, 4) dan (8, 0).
* Gambar garis x = 0 dan y = 0 untuk mendefinisikan kuadran pertama.
5. Menentukan area solusi:
* Area solusi adalah wilayah yang memenuhi semua kendala, yaitu di bawah garis 2x + y = 10, di bawah garis x + 2y = 8, dan di kuadran pertama.
6. Menentukan titik-titik sudut:
* Titik sudut area solusi adalah (0, 0), (0, 4), (4, 2), dan (5, 0).
7. Menghitung nilai fungsi tujuan pada setiap titik sudut:
* (0, 0): 10.000(0) + 15.000(0) = 0
* (0, 4): 10.000(0) + 15.000(4) = 60.000
* (4, 2): 10.000(4) + 15.000(2) = 70.000
* (5, 0): 10.000(5) + 15.000(0) = 50.000
8. Menentukan titik optimum:
* Titik optimum adalah (4, 2), karena memberikan keuntungan maksimum sebesar Rp 70.000.
Ilustrasi Grafik:
[Ilustrasi grafik menunjukkan area solusi dan titik optimum dengan garis kendala dan titik-titik sudut yang diberi label.]
Metode Simpleks
Metode simpleks merupakan salah satu metode yang umum digunakan untuk menyelesaikan masalah program linear. Metode ini efektif untuk mencari solusi optimal dari masalah program linear dengan beberapa kendala.
Cara Menyelesaikan Program Linear dengan Metode Simpleks, Contoh soal program linear dan jawabannya
Metode simpleks bekerja dengan membangun tabel yang berisi koefisien dari persamaan kendala dan fungsi tujuan. Tabel ini disebut tabel simpleks. Berikut langkah-langkah menyelesaikan program linear dengan metode simpleks:
- Ubah masalah program linear ke bentuk standar. Bentuk standar program linear memiliki persamaan kendala yang berupa persamaan dengan tanda sama dengan (=) dan semua variabel non-negatif.
- Buat tabel simpleks. Tabel simpleks berisi koefisien dari persamaan kendala dan fungsi tujuan. Kolom pertama tabel berisi variabel-variabel, baris pertama berisi nama kendala dan fungsi tujuan, dan isi tabel berisi koefisien dari persamaan kendala dan fungsi tujuan.
- Pilih variabel masuk. Variabel masuk adalah variabel yang akan dimasukkan ke dalam basis. Variabel masuk dipilih dari variabel yang memiliki koefisien negatif terbesar dalam baris fungsi tujuan.
- Pilih variabel keluar. Variabel keluar adalah variabel yang akan dikeluarkan dari basis. Variabel keluar dipilih dari variabel yang memiliki rasio terkecil antara nilai konstanta pada kolom variabel masuk dengan koefisien variabel masuk pada baris kendala.
- Ubah tabel simpleks. Setelah variabel masuk dan variabel keluar dipilih, tabel simpleks diubah dengan menggunakan operasi baris elementer. Operasi baris elementer dilakukan untuk membuat koefisien variabel masuk menjadi 1 dan koefisien variabel masuk lainnya menjadi 0.
- Ulangi langkah 3-5 hingga semua koefisien dalam baris fungsi tujuan non-negatif. Jika semua koefisien dalam baris fungsi tujuan non-negatif, maka solusi optimal telah ditemukan.
Contoh Soal Program Linear dan Penyelesaian dengan Metode Simpleks
Sebuah perusahaan memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku, sedangkan produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku. Perusahaan memiliki 10 jam waktu produksi dan 8 kg bahan baku. Keuntungan yang diperoleh dari penjualan produk A adalah Rp. 50.000,- per unit, sedangkan keuntungan dari penjualan produk B adalah Rp. 40.000,- per unit. Berapakah jumlah produk A dan B yang harus diproduksi agar keuntungan maksimal?
Berikut langkah-langkah menyelesaikan soal program linear dengan metode simpleks:
- Tentukan fungsi tujuan dan kendala.
- Fungsi tujuan: Maksimalkan keuntungan (Z) = 50.000A + 40.000B
- Kendala:
- 2A + B ≤ 10 (kendala waktu produksi)
- A + 2B ≤ 8 (kendala bahan baku)
- A ≥ 0, B ≥ 0 (kendala non-negatif)
- Ubah kendala ke bentuk standar.
- 2A + B + S1 = 10
- A + 2B + S2 = 8
- A ≥ 0, B ≥ 0, S1 ≥ 0, S2 ≥ 0
S1 dan S2 adalah variabel slack yang digunakan untuk mengubah tanda pertidaksamaan menjadi persamaan.
- Buat tabel simpleks.
Variabel A B S1 S2 Konstanta S1 2 1 1 0 10 S2 1 2 0 1 8 Z -50.000 -40.000 0 0 0 - Pilih variabel masuk.
- Variabel A memiliki koefisien negatif terbesar dalam baris fungsi tujuan (Z), yaitu -50.000. Oleh karena itu, variabel A dipilih sebagai variabel masuk.
- Pilih variabel keluar.
- Hitung rasio antara nilai konstanta dengan koefisien variabel masuk pada setiap baris kendala:
- Baris S1: 10/2 = 5
- Baris S2: 8/1 = 8
- Rasio terkecil adalah 5, yang terdapat pada baris S1. Oleh karena itu, variabel S1 dipilih sebagai variabel keluar.
- Hitung rasio antara nilai konstanta dengan koefisien variabel masuk pada setiap baris kendala:
- Ubah tabel simpleks.
- Buat koefisien variabel masuk (A) pada baris S1 menjadi 1 dengan membagi baris S1 dengan 2.
- Buat koefisien variabel masuk (A) pada baris S2 dan Z menjadi 0 dengan melakukan operasi baris elementer.
- Baris S2: Baris S2 – (1/2) * Baris S1
- Baris Z: Baris Z + 50.000 * Baris S1
Variabel A B S1 S2 Konstanta A 1 1/2 1/2 0 5 S2 0 3/2 -1/2 1 3 Z 0 -15.000 25.000 0 250.000 - Ulangi langkah 4-6 hingga semua koefisien dalam baris fungsi tujuan non-negatif.
- Variabel B memiliki koefisien negatif dalam baris fungsi tujuan (Z), yaitu -15.000. Oleh karena itu, variabel B dipilih sebagai variabel masuk.
- Hitung rasio antara nilai konstanta dengan koefisien variabel masuk pada setiap baris kendala:
- Baris A: 5/(1/2) = 10
- Baris S2: 3/(3/2) = 2
- Rasio terkecil adalah 2, yang terdapat pada baris S2. Oleh karena itu, variabel S2 dipilih sebagai variabel keluar.
- Buat koefisien variabel masuk (B) pada baris S2 menjadi 1 dengan membagi baris S2 dengan (3/2).
- Buat koefisien variabel masuk (B) pada baris A dan Z menjadi 0 dengan melakukan operasi baris elementer.
- Baris A: Baris A – (1/2) * Baris S2
- Baris Z: Baris Z + 15.000 * Baris S2
Variabel A B S1 S2 Konstanta A 1 0 2/3 -1/3 4 B 0 1 -1/3 2/3 2 Z 0 0 20.000 10.000 280.000 - Solusi optimal telah ditemukan.
- Semua koefisien dalam baris fungsi tujuan non-negatif. Oleh karena itu, solusi optimal telah ditemukan.
- Solusi optimal: A = 4, B = 2, Z = 280.000
Kesimpulan: Perusahaan harus memproduksi 4 unit produk A dan 2 unit produk B untuk mendapatkan keuntungan maksimal sebesar Rp. 280.000,-.
Aplikasi Program Linear
Program linear merupakan alat yang sangat berguna dalam memecahkan berbagai masalah optimasi yang melibatkan pembatasan sumber daya dan tujuan yang ingin dicapai. Aplikasi program linear sangat luas, mulai dari ekonomi dan bisnis hingga industri dan berbagai bidang lainnya.
Aplikasi Program Linear dalam Ekonomi
Program linear memiliki peran penting dalam berbagai aspek ekonomi, seperti:
- Manajemen Produksi: Program linear membantu perusahaan menentukan jumlah optimal dari berbagai produk yang harus diproduksi untuk memaksimalkan keuntungan dengan mempertimbangkan keterbatasan sumber daya seperti tenaga kerja, bahan baku, dan kapasitas produksi.
- Perencanaan Ekonomi: Program linear dapat digunakan untuk merancang rencana ekonomi nasional yang optimal, misalnya dalam menentukan alokasi sumber daya yang tepat untuk berbagai sektor ekonomi untuk mencapai pertumbuhan ekonomi yang maksimal.
- Analisis Pasar: Program linear dapat digunakan untuk menganalisis pasar dan menentukan strategi pemasaran yang optimal, seperti menentukan harga jual produk yang optimal untuk memaksimalkan keuntungan dengan mempertimbangkan permintaan pasar dan persaingan.
Aplikasi Program Linear dalam Bisnis
Program linear memiliki aplikasi yang luas dalam berbagai bidang bisnis, seperti:
- Manajemen Inventaris: Program linear dapat digunakan untuk menentukan jumlah optimal inventaris yang harus disimpan untuk memenuhi permintaan pelanggan dengan meminimalkan biaya penyimpanan dan kekurangan inventaris.
- Perencanaan Produksi: Program linear membantu perusahaan menentukan jumlah optimal dari berbagai produk yang harus diproduksi untuk memaksimalkan keuntungan dengan mempertimbangkan keterbatasan sumber daya seperti tenaga kerja, bahan baku, dan kapasitas produksi.
- Manajemen Pemasaran: Program linear dapat digunakan untuk menentukan strategi pemasaran yang optimal, seperti menentukan alokasi anggaran pemasaran yang tepat untuk berbagai media promosi untuk mencapai target pasar yang maksimal.
Aplikasi Program Linear dalam Industri
Program linear memiliki banyak aplikasi dalam berbagai industri, seperti:
- Perencanaan Produksi: Program linear dapat digunakan untuk menentukan jadwal produksi yang optimal dengan mempertimbangkan keterbatasan sumber daya dan permintaan pasar, meminimalkan biaya produksi dan memaksimalkan efisiensi.
- Manajemen Logistik: Program linear dapat digunakan untuk merancang rute pengiriman yang optimal untuk meminimalkan biaya transportasi dan waktu pengiriman.
- Pengaturan Jadwal Kerja: Program linear dapat digunakan untuk mengatur jadwal kerja karyawan yang optimal dengan mempertimbangkan kebutuhan produksi, ketersediaan karyawan, dan peraturan ketenagakerjaan.
Bagaimana Program Linear Membantu Pengambilan Keputusan?
Program linear membantu dalam pengambilan keputusan dengan memberikan solusi optimal untuk masalah yang kompleks. Dengan menggunakan model matematika yang mewakili situasi nyata, program linear dapat menentukan kombinasi terbaik dari berbagai variabel untuk mencapai tujuan yang diinginkan.
Manfaat Penggunaan Program Linear
Berikut adalah beberapa manfaat dari penggunaan program linear dalam memecahkan masalah optimasi:
- Solusi Optimal: Program linear memberikan solusi optimal untuk masalah yang kompleks dengan mempertimbangkan semua pembatasan dan tujuan yang ditetapkan.
- Efisiensi: Program linear membantu dalam mengoptimalkan penggunaan sumber daya yang terbatas, seperti tenaga kerja, bahan baku, dan waktu, sehingga meningkatkan efisiensi dan produktivitas.
- Pengambilan Keputusan yang Lebih Baik: Program linear memberikan dasar yang kuat untuk pengambilan keputusan dengan memberikan informasi yang objektif dan terstruktur, sehingga membantu dalam membuat keputusan yang lebih tepat dan efektif.
- Peningkatan Keuntungan: Program linear dapat membantu dalam memaksimalkan keuntungan dengan menentukan strategi produksi, pemasaran, dan operasional yang optimal.
- Pengurangan Biaya: Program linear dapat membantu dalam meminimalkan biaya produksi, transportasi, dan operasional dengan menentukan solusi yang optimal.
Solusi Optimal
Solusi optimal dalam program linear merupakan titik yang menghasilkan nilai maksimum atau minimum dari fungsi tujuan (objective function) yang memenuhi semua kendala (constraints). Titik ini mewakili solusi terbaik yang dapat dicapai dalam model program linear.
Cara Menentukan Solusi Optimal
Solusi optimal dapat ditentukan dengan menggunakan metode grafik atau metode Simplex. Metode grafik lebih mudah dipahami dan cocok untuk model program linear dengan dua variabel, sedangkan metode Simplex lebih kompleks tetapi dapat digunakan untuk model dengan lebih banyak variabel.
Contoh Soal dan Solusi Optimal
Misalnya, sebuah perusahaan memproduksi dua jenis produk, A dan B. Setiap produk memerlukan waktu produksi tertentu dan sumber daya yang terbatas. Tujuan perusahaan adalah untuk memaksimalkan keuntungan. Berikut adalah model program linearnya:
| Variabel | Keterangan |
|---|---|
| x | Jumlah produk A yang diproduksi |
| y | Jumlah produk B yang diproduksi |
Fungsi tujuan (memaksimalkan keuntungan):
Z = 5x + 7y
Kendala (waktu produksi dan sumber daya):
x + 2y ≤ 10
3x + y ≤ 12
x ≥ 0, y ≥ 0
Untuk menentukan solusi optimal, kita dapat menggunakan metode grafik. Kita akan menggambar garis yang mewakili kendala dan mencari titik yang memenuhi semua kendala dan memaksimalkan fungsi tujuan.
Setelah menggambar grafik, kita akan menemukan titik yang memenuhi semua kendala dan memaksimalkan fungsi tujuan. Titik ini adalah solusi optimal. Dalam contoh ini, solusi optimal adalah (x, y) = (2, 4), yang menghasilkan keuntungan maksimum sebesar Z = 38.
Perbedaan Solusi Optimal dan Solusi Layak
Solusi layak adalah titik yang memenuhi semua kendala dalam model program linear. Solusi optimal adalah solusi layak yang menghasilkan nilai maksimum atau minimum dari fungsi tujuan. Dengan kata lain, solusi optimal adalah solusi layak terbaik.
Tidak semua solusi layak adalah solusi optimal. Misalnya, dalam contoh di atas, titik (x, y) = (0, 0) adalah solusi layak karena memenuhi semua kendala. Namun, titik ini tidak menghasilkan keuntungan maksimum. Solusi optimal adalah titik yang menghasilkan keuntungan maksimum, yaitu (x, y) = (2, 4).
Interpretasi Solusi: Contoh Soal Program Linear Dan Jawabannya
Setelah mendapatkan solusi optimal dari program linear, langkah selanjutnya adalah menginterpretasikannya. Interpretasi solusi optimal sangat penting karena memberikan makna praktis terhadap hasil perhitungan matematis. Dengan memahami interpretasi solusi, kita dapat mengambil keputusan yang tepat berdasarkan model program linear yang telah kita buat.
Cara Menginterpretasikan Solusi Optimal
Solusi optimal dari program linear biasanya berupa nilai variabel keputusan yang memaksimalkan atau meminimalkan fungsi tujuan. Untuk menginterpretasikan solusi optimal, kita perlu memahami arti dari setiap variabel keputusan dan nilai yang diperoleh.
Contoh soal program linear dan jawabannya bisa kita temukan di berbagai buku pelajaran matematika. Soal-soal ini biasanya membahas tentang cara mencari nilai optimal dari suatu fungsi linear dengan batasan tertentu. Nah, mirip dengan program linear, kita juga bisa menemukan contoh soal yang berkaitan dengan konsep fisika, seperti momen inersia.
Sebagai contoh, kita bisa menemukan contoh soal momen inersia bola pejal di sini. Contoh soal momen inersia ini membantu kita memahami bagaimana menghitung momen inersia bola pejal, yang penting untuk mempelajari dinamika rotasi. Kembali ke program linear, contoh soal dan jawabannya sangat membantu untuk memahami konsep dan menyelesaikan soal-soal yang lebih kompleks.
- Identifikasi setiap variabel keputusan dan apa yang diwakilinya dalam konteks masalah.
- Perhatikan nilai optimal yang diperoleh untuk setiap variabel keputusan.
- Hubungkan nilai optimal dengan makna variabel keputusan dan tujuan masalah.
Contoh Soal Program Linear dan Interpretasi Solusi Optimalnya
Misalkan sebuah perusahaan memproduksi dua jenis produk, yaitu produk A dan produk B. Perusahaan ingin menentukan jumlah produksi untuk setiap produk yang dapat memaksimalkan keuntungan. Diketahui bahwa:
- Keuntungan per unit produk A adalah Rp 10.000 dan keuntungan per unit produk B adalah Rp 15.000.
- Waktu produksi untuk satu unit produk A adalah 2 jam dan waktu produksi untuk satu unit produk B adalah 3 jam.
- Total waktu produksi yang tersedia adalah 120 jam.
- Bahan baku yang dibutuhkan untuk memproduksi satu unit produk A adalah 1 kg dan bahan baku yang dibutuhkan untuk memproduksi satu unit produk B adalah 2 kg.
- Total bahan baku yang tersedia adalah 60 kg.
Model program linear untuk masalah ini dapat ditulis sebagai berikut:
Max Z = 10.000A + 15.000B (Fungsi Tujuan)
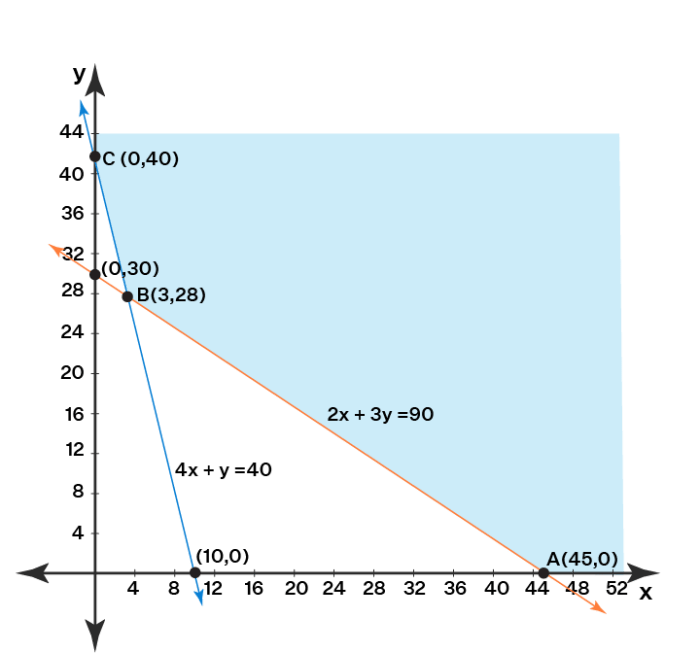
2A + 3B ≤ 120 (Kendala Waktu)
A + 2B ≤ 60 (Kendala Bahan Baku)
A, B ≥ 0 (Kendala Non-Negatif)
Setelah menyelesaikan program linear ini, kita mendapatkan solusi optimal yaitu A = 30 dan B = 20. Artinya, untuk memaksimalkan keuntungan, perusahaan harus memproduksi 30 unit produk A dan 20 unit produk B. Keuntungan maksimal yang dapat diperoleh adalah Rp 600.000.
Penggunaan Solusi Optimal untuk Pengambilan Keputusan
Interpretasi solusi optimal sangat penting untuk pengambilan keputusan dalam berbagai bidang, seperti:
- Perencanaan Produksi: Solusi optimal membantu menentukan jumlah produksi yang tepat untuk memaksimalkan keuntungan atau meminimalkan biaya.
- Manajemen Inventaris: Solusi optimal membantu menentukan jumlah persediaan yang optimal untuk memenuhi permintaan pelanggan dengan biaya penyimpanan yang minimal.
- Alokasi Sumber Daya: Solusi optimal membantu mengalokasikan sumber daya yang terbatas (misalnya, tenaga kerja, bahan baku, atau modal) secara efisien untuk mencapai tujuan yang diinginkan.
- Pengambilan Keputusan Investasi: Solusi optimal membantu menentukan portofolio investasi yang optimal untuk memaksimalkan pengembalian dengan risiko yang terkontrol.
Contoh Soal Program Linear
Program linear adalah salah satu cabang ilmu matematika yang mempelajari tentang cara memaksimalkan atau meminimalkan suatu fungsi linear dengan batasan-batasan yang juga linear. Program linear banyak diterapkan dalam berbagai bidang, seperti ekonomi, bisnis, dan ilmu komputer. Untuk memahami program linear lebih dalam, berikut beberapa contoh soal latihan.
Contoh Soal Program Linear
Berikut ini adalah beberapa contoh soal program linear yang bisa Anda coba selesaikan:
-
Sebuah perusahaan memproduksi dua jenis produk, yaitu produk A dan produk B. Untuk memproduksi produk A, dibutuhkan 2 jam tenaga kerja dan 1 kg bahan baku. Untuk memproduksi produk B, dibutuhkan 1 jam tenaga kerja dan 2 kg bahan baku. Perusahaan memiliki 100 jam tenaga kerja dan 80 kg bahan baku. Keuntungan per unit produk A adalah Rp 10.000 dan keuntungan per unit produk B adalah Rp 15.000. Berapakah jumlah produk A dan produk B yang harus diproduksi agar keuntungan maksimal?
Petunjuk:
- Tentukan variabel-variabel yang akan digunakan dalam model program linear.
- Tentukan fungsi objektif yang ingin dimaksimalkan (dalam hal ini keuntungan).
- Tentukan batasan-batasan yang berlaku.
- Selesaikan model program linear menggunakan metode grafik atau metode simplex.
-
Seorang petani ingin menanam dua jenis tanaman, yaitu tanaman A dan tanaman B. Untuk menanam tanaman A, dibutuhkan 10 kg pupuk dan 5 liter air. Untuk menanam tanaman B, dibutuhkan 5 kg pupuk dan 10 liter air. Petani memiliki 100 kg pupuk dan 50 liter air. Keuntungan per hektar tanaman A adalah Rp 2.000.000 dan keuntungan per hektar tanaman B adalah Rp 3.000.000. Berapakah luas lahan yang harus ditanami tanaman A dan tanaman B agar keuntungan maksimal?
Petunjuk:
- Tentukan variabel-variabel yang akan digunakan dalam model program linear.
- Tentukan fungsi objektif yang ingin dimaksimalkan (dalam hal ini keuntungan).
- Tentukan batasan-batasan yang berlaku.
- Selesaikan model program linear menggunakan metode grafik atau metode simplex.
-
Sebuah perusahaan memiliki dua jenis mesin, yaitu mesin A dan mesin B. Mesin A dapat memproduksi 10 unit produk per jam dan mesin B dapat memproduksi 15 unit produk per jam. Perusahaan memiliki 10 jam waktu produksi. Biaya operasional mesin A adalah Rp 50.000 per jam dan biaya operasional mesin B adalah Rp 70.000 per jam. Berapakah waktu yang harus digunakan untuk mengoperasikan masing-masing mesin agar biaya operasional minimal dan jumlah produk yang dihasilkan maksimal?
Petunjuk:
- Tentukan variabel-variabel yang akan digunakan dalam model program linear.
- Tentukan fungsi objektif yang ingin diminimalkan (dalam hal ini biaya operasional).
- Tentukan batasan-batasan yang berlaku.
- Selesaikan model program linear menggunakan metode grafik atau metode simplex.
-
Seorang pedagang ingin membeli dua jenis barang, yaitu barang A dan barang B. Harga barang A adalah Rp 10.000 per unit dan harga barang B adalah Rp 15.000 per unit. Pedagang memiliki modal Rp 1.000.000. Keuntungan per unit barang A adalah Rp 2.000 dan keuntungan per unit barang B adalah Rp 3.000. Berapakah jumlah barang A dan barang B yang harus dibeli agar keuntungan maksimal?
Petunjuk:
- Tentukan variabel-variabel yang akan digunakan dalam model program linear.
- Tentukan fungsi objektif yang ingin dimaksimalkan (dalam hal ini keuntungan).
- Tentukan batasan-batasan yang berlaku.
- Selesaikan model program linear menggunakan metode grafik atau metode simplex.
-
Sebuah perusahaan ingin memproduksi dua jenis produk, yaitu produk A dan produk B. Untuk memproduksi produk A, dibutuhkan 3 jam tenaga kerja dan 2 kg bahan baku. Untuk memproduksi produk B, dibutuhkan 2 jam tenaga kerja dan 3 kg bahan baku. Perusahaan memiliki 120 jam tenaga kerja dan 100 kg bahan baku. Keuntungan per unit produk A adalah Rp 5.000 dan keuntungan per unit produk B adalah Rp 7.000. Berapakah jumlah produk A dan produk B yang harus diproduksi agar keuntungan maksimal?
Petunjuk:
- Tentukan variabel-variabel yang akan digunakan dalam model program linear.
- Tentukan fungsi objektif yang ingin dimaksimalkan (dalam hal ini keuntungan).
- Tentukan batasan-batasan yang berlaku.
- Selesaikan model program linear menggunakan metode grafik atau metode simplex.
Tabel Soal dan Jawaban
| Soal | Jawaban |
|---|---|
| Sebuah perusahaan memproduksi dua jenis produk, yaitu produk A dan produk B. Untuk memproduksi produk A, dibutuhkan 2 jam tenaga kerja dan 1 kg bahan baku. Untuk memproduksi produk B, dibutuhkan 1 jam tenaga kerja dan 2 kg bahan baku. Perusahaan memiliki 100 jam tenaga kerja dan 80 kg bahan baku. Keuntungan per unit produk A adalah Rp 10.000 dan keuntungan per unit produk B adalah Rp 15.000. Berapakah jumlah produk A dan produk B yang harus diproduksi agar keuntungan maksimal? | Jumlah produk A yang harus diproduksi adalah 20 unit dan jumlah produk B yang harus diproduksi adalah 30 unit. Keuntungan maksimal yang dapat dicapai adalah Rp 650.000. |
| Seorang petani ingin menanam dua jenis tanaman, yaitu tanaman A dan tanaman B. Untuk menanam tanaman A, dibutuhkan 10 kg pupuk dan 5 liter air. Untuk menanam tanaman B, dibutuhkan 5 kg pupuk dan 10 liter air. Petani memiliki 100 kg pupuk dan 50 liter air. Keuntungan per hektar tanaman A adalah Rp 2.000.000 dan keuntungan per hektar tanaman B adalah Rp 3.000.000. Berapakah luas lahan yang harus ditanami tanaman A dan tanaman B agar keuntungan maksimal? | Luas lahan yang harus ditanami tanaman A adalah 5 hektar dan luas lahan yang harus ditanami tanaman B adalah 5 hektar. Keuntungan maksimal yang dapat dicapai adalah Rp 25.000.000. |
| Sebuah perusahaan memiliki dua jenis mesin, yaitu mesin A dan mesin B. Mesin A dapat memproduksi 10 unit produk per jam dan mesin B dapat memproduksi 15 unit produk per jam. Perusahaan memiliki 10 jam waktu produksi. Biaya operasional mesin A adalah Rp 50.000 per jam dan biaya operasional mesin B adalah Rp 70.000 per jam. Berapakah waktu yang harus digunakan untuk mengoperasikan masing-masing mesin agar biaya operasional minimal dan jumlah produk yang dihasilkan maksimal? | Waktu yang harus digunakan untuk mengoperasikan mesin A adalah 6 jam dan waktu yang harus digunakan untuk mengoperasikan mesin B adalah 4 jam. Biaya operasional minimal yang dapat dicapai adalah Rp 580.000 dan jumlah produk yang dihasilkan maksimal adalah 120 unit. |
| Seorang pedagang ingin membeli dua jenis barang, yaitu barang A dan barang B. Harga barang A adalah Rp 10.000 per unit dan harga barang B adalah Rp 15.000 per unit. Pedagang memiliki modal Rp 1.000.000. Keuntungan per unit barang A adalah Rp 2.000 dan keuntungan per unit barang B adalah Rp 3.000. Berapakah jumlah barang A dan barang B yang harus dibeli agar keuntungan maksimal? | Jumlah barang A yang harus dibeli adalah 50 unit dan jumlah barang B yang harus dibeli adalah 33 unit. Keuntungan maksimal yang dapat dicapai adalah Rp 219.000. |
| Sebuah perusahaan ingin memproduksi dua jenis produk, yaitu produk A dan produk B. Untuk memproduksi produk A, dibutuhkan 3 jam tenaga kerja dan 2 kg bahan baku. Untuk memproduksi produk B, dibutuhkan 2 jam tenaga kerja dan 3 kg bahan baku. Perusahaan memiliki 120 jam tenaga kerja dan 100 kg bahan baku. Keuntungan per unit produk A adalah Rp 5.000 dan keuntungan per unit produk B adalah Rp 7.000. Berapakah jumlah produk A dan produk B yang harus diproduksi agar keuntungan maksimal? | Jumlah produk A yang harus diproduksi adalah 20 unit dan jumlah produk B yang harus diproduksi adalah 20 unit. Keuntungan maksimal yang dapat dicapai adalah Rp 240.000. |
Perangkat Lunak Program Linear
Program linear merupakan metode optimasi yang sangat berguna untuk menyelesaikan masalah pengambilan keputusan dengan berbagai kendala. Namun, menyelesaikannya secara manual dapat menjadi rumit, terutama untuk masalah dengan banyak variabel dan kendala. Untuk mengatasi hal ini, perangkat lunak program linear hadir sebagai solusi yang praktis dan efisien.
Fungsi Perangkat Lunak Program Linear
Perangkat lunak program linear dirancang untuk membantu pengguna dalam menyelesaikan masalah optimasi dengan metode program linear. Fungsi utamanya adalah:
- Membantu dalam mendefinisikan model program linear, yaitu mengidentifikasi variabel keputusan, fungsi objektif, dan kendala.
- Melakukan perhitungan dan analisis untuk menemukan solusi optimal, yaitu nilai variabel keputusan yang memaksimalkan atau meminimalkan fungsi objektif sesuai dengan kendala yang ada.
- Memvisualisasikan solusi optimal dalam bentuk grafik atau tabel, sehingga memudahkan pemahaman dan interpretasi hasil.
- Memberikan informasi tambahan seperti sensitivitas analisis, yaitu bagaimana perubahan nilai parameter mempengaruhi solusi optimal.
Contoh Perangkat Lunak Program Linear yang Populer
Beberapa perangkat lunak program linear yang populer dan banyak digunakan antara lain:
- Lingo: Merupakan perangkat lunak yang khusus dirancang untuk menyelesaikan masalah program linear, dengan antarmuka yang mudah digunakan dan fitur yang lengkap.
- Solver: Tersedia sebagai add-in untuk Microsoft Excel, Solver dapat digunakan untuk menyelesaikan masalah program linear dan non-linear dengan berbagai jenis kendala.
- Gurobi Optimizer: Merupakan perangkat lunak yang canggih dan efisien untuk menyelesaikan masalah program linear dan non-linear skala besar.
- IBM ILOG CPLEX Optimizer: Serupa dengan Gurobi Optimizer, CPLEX Optimizer merupakan perangkat lunak yang powerful dan sering digunakan untuk menyelesaikan masalah optimasi yang kompleks.
Langkah-langkah Menggunakan Perangkat Lunak Program Linear
Secara umum, langkah-langkah dalam menggunakan perangkat lunak program linear adalah sebagai berikut:
- Definisikan model program linear: Tentukan variabel keputusan, fungsi objektif, dan kendala yang ingin dipecahkan.
- Masukkan data ke dalam perangkat lunak: Masukkan data yang terkait dengan variabel keputusan, fungsi objektif, dan kendala ke dalam perangkat lunak.
- Jalankan algoritma program linear: Perangkat lunak akan menggunakan algoritma program linear untuk menemukan solusi optimal.
- Analisis hasil: Periksa hasil yang ditampilkan oleh perangkat lunak, termasuk solusi optimal, nilai variabel keputusan, dan informasi tambahan seperti sensitivitas analisis.
Ringkasan Akhir
Memahami program linear membuka jalan bagi kita untuk menyelesaikan berbagai masalah optimasi dalam kehidupan sehari-hari, mulai dari perencanaan produksi di pabrik hingga penentuan rute pengiriman yang paling efisien. Dengan kemampuan memodelkan masalah dan menemukan solusi optimal, program linear menjadi alat yang sangat berharga dalam berbagai bidang seperti ekonomi, bisnis, dan industri.





