Contoh soal program linear dan penyelesaiannya – Program linear merupakan alat yang ampuh untuk menyelesaikan berbagai masalah optimasi dalam kehidupan sehari-hari, seperti menentukan strategi produksi optimal, meminimalkan biaya, atau memaksimalkan keuntungan. Dalam artikel ini, kita akan menjelajahi dunia program linear dengan mempelajari konsep dasar, metode penyelesaian, dan contoh-contoh menarik yang menunjukkan penerapannya dalam berbagai bidang.
Kita akan membahas dua metode utama dalam menyelesaikan program linear, yaitu metode grafik dan metode simplex. Dengan contoh soal dan ilustrasi yang jelas, Anda akan memahami bagaimana kedua metode ini bekerja dan bagaimana memilih metode yang tepat untuk menyelesaikan masalah tertentu. Selain itu, kita juga akan membahas penerapan program linear dalam berbagai bidang, seperti ekonomi, bisnis, dan industri, untuk menunjukkan bagaimana program linear dapat membantu dalam pengambilan keputusan yang optimal.
Pengertian Program Linear
Program linear adalah metode matematika yang digunakan untuk mencari solusi optimal dari suatu masalah yang melibatkan variabel-variabel terbatas dengan batasan-batasan tertentu. Dalam program linear, semua hubungan antar variabel dan batasan dinyatakan dalam bentuk persamaan atau pertidaksamaan linear.
Contoh Permasalahan Sehari-hari
Sebagai contoh, perhatikan seorang pengusaha yang ingin memproduksi dua jenis produk, yaitu produk A dan produk B. Setiap produk memerlukan bahan baku yang berbeda, dan pengusaha ini memiliki keterbatasan bahan baku. Ia juga ingin memaksimalkan keuntungan yang diperoleh dari penjualan kedua produk tersebut.
Rumus Umum Program Linear
Dalam program linear, masalah dimodelkan dengan menggunakan fungsi objektif dan kendala.
Fungsi Objektif
Fungsi objektif adalah fungsi matematika yang ingin dioptimalkan (dimaksimalkan atau diminimalkan). Fungsi objektif biasanya dinyatakan dalam bentuk:
Z = c1x1 + c2x2 + … + cnxn
di mana:
* Z adalah nilai fungsi objektif
* ci adalah koefisien variabel ke-i
* xi adalah variabel ke-i
Kendala
Kendala adalah batasan-batasan yang harus dipenuhi dalam menyelesaikan masalah program linear. Kendala biasanya dinyatakan dalam bentuk pertidaksamaan linear:
a1x1 + a2x2 + … + anxn ≤ b1
a1x1 + a2x2 + … + anxn ≥ b2
a1x1 + a2x2 + … + anxn = b3
di mana:
* ai adalah koefisien variabel ke-i
* xi adalah variabel ke-i
* bi adalah konstanta
Metode Penyelesaian Program Linear
Ada beberapa metode yang dapat digunakan untuk menyelesaikan masalah program linear, antara lain:
- Metode Grafik
- Metode Simplex
- Metode Dualitas
Metode Grafik
Metode grafik merupakan salah satu metode yang digunakan untuk menyelesaikan program linear. Metode ini melibatkan penggambaran garis yang mewakili kendala-kendala dalam program linear, kemudian menentukan titik optimum yang memenuhi semua kendala dan memaksimalkan atau meminimalkan fungsi objektif.
Langkah-langkah Menyelesaikan Program Linear dengan Metode Grafik
Langkah-langkah dalam menyelesaikan program linear dengan metode grafik adalah sebagai berikut:
- Tentukan fungsi objektif dan kendala-kendala dalam program linear.
- Ubah setiap kendala menjadi persamaan garis. Untuk melakukan ini, ganti tanda pertidaksamaan dengan tanda sama dengan.
- Gambar garis-garis yang mewakili kendala-kendala pada bidang koordinat. Untuk menentukan titik potong sumbu, substitusikan nilai x = 0 dan y = 0 ke dalam persamaan garis.
- Tentukan daerah yang memenuhi semua kendala. Daerah ini disebut daerah feasible atau daerah penyelesaian.
- Tentukan titik-titik sudut dari daerah feasible. Titik-titik sudut adalah titik-titik yang terletak pada perpotongan garis-garis kendala.
- Hitung nilai fungsi objektif pada setiap titik sudut. Titik sudut yang menghasilkan nilai fungsi objektif maksimum atau minimum adalah titik optimum.
Contoh Soal Program Linear dan Penyelesaiannya dengan Metode Grafik
Sebuah perusahaan memproduksi dua jenis produk, A dan B. Setiap unit produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku, sedangkan setiap unit produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku. Perusahaan memiliki 40 jam waktu produksi dan 30 kg bahan baku. Keuntungan per unit produk A adalah Rp 10.000, sedangkan keuntungan per unit produk B adalah Rp 15.000. Berapa banyak produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan?
Berikut adalah langkah-langkah menyelesaikan soal program linear dengan metode grafik:
- Tentukan fungsi objektif dan kendala-kendala dalam program linear.
Fungsi objektif:
Maksimumkan keuntungan = 10.000A + 15.000B
Kendala:
2A + B ≤ 40 (kendala waktu produksi)
A + 2B ≤ 30 (kendala bahan baku)
A ≥ 0 (kendala non-negatif)
B ≥ 0 (kendala non-negatif) - Ubah setiap kendala menjadi persamaan garis.
2A + B = 40
A + 2B = 30
A = 0
B = 0 - Gambar garis-garis yang mewakili kendala-kendala pada bidang koordinat.
- Untuk garis 2A + B = 40:
- Jika A = 0, maka B = 40.
- Jika B = 0, maka A = 20.
- Untuk garis A + 2B = 30:
- Jika A = 0, maka B = 15.
- Jika B = 0, maka A = 30.
- Untuk garis A = 0, garisnya adalah sumbu vertikal.
- Untuk garis B = 0, garisnya adalah sumbu horizontal.
- Untuk garis 2A + B = 40:
- Tentukan daerah yang memenuhi semua kendala. Daerah feasible adalah daerah yang berada di bawah garis 2A + B = 40, di bawah garis A + 2B = 30, di sebelah kanan sumbu vertikal, dan di atas sumbu horizontal.
- Tentukan titik-titik sudut dari daerah feasible. Titik-titik sudut adalah (0, 0), (0, 15), (10, 20), dan (20, 0).
- Hitung nilai fungsi objektif pada setiap titik sudut.
- Pada titik (0, 0), keuntungan = 10.000(0) + 15.000(0) = 0
- Pada titik (0, 15), keuntungan = 10.000(0) + 15.000(15) = 225.000
- Pada titik (10, 20), keuntungan = 10.000(10) + 15.000(20) = 400.000
- Pada titik (20, 0), keuntungan = 10.000(20) + 15.000(0) = 200.000
- Titik optimum adalah titik yang menghasilkan nilai fungsi objektif maksimum. Dalam kasus ini, titik optimum adalah (10, 20) dengan keuntungan maksimum Rp 400.000.
Cara Menentukan Titik Optimum pada Grafik
Titik optimum pada grafik dapat ditentukan dengan melihat titik sudut dari daerah feasible yang menghasilkan nilai fungsi objektif maksimum atau minimum. Titik optimum dapat diidentifikasi dengan cara:
- Membuat garis yang sejajar dengan garis fungsi objektif. Garis ini disebut garis isoprofit.
- Geser garis isoprofit ke arah yang memaksimalkan atau meminimalkan fungsi objektif.
- Titik sudut dari daerah feasible yang dilalui oleh garis isoprofit pada posisi maksimum atau minimum adalah titik optimum.
Metode Simplex
Metode Simplex merupakan algoritma yang digunakan untuk menyelesaikan masalah program linear. Metode ini secara sistematis mengevaluasi solusi-solusi yang memungkinkan untuk menemukan solusi optimal yang memaksimalkan atau meminimalkan fungsi objektif.
Langkah-langkah Metode Simplex, Contoh soal program linear dan penyelesaiannya
Metode Simplex bekerja dengan mengubah masalah program linear menjadi bentuk standar dan kemudian menerapkan serangkaian langkah iteratif untuk menemukan solusi optimal. Berikut adalah langkah-langkah dalam metode Simplex:
- Bentuk Standar: Ubah masalah program linear menjadi bentuk standar. Ini melibatkan mengubah semua kendala menjadi persamaan dengan menambahkan variabel slack, dan memastikan bahwa semua koefisien pada sisi kanan persamaan adalah non-negatif.
- Buat Tabel Simplex: Buat tabel simplex yang berisi koefisien dari variabel keputusan, variabel slack, dan fungsi objektif. Tabel ini akan digunakan untuk melacak iterasi metode simplex.
- Pilih Variabel Masuk: Tentukan variabel yang akan dimasukkan ke dalam basis. Ini biasanya variabel dengan koefisien paling positif dalam baris fungsi objektif.
- Pilih Variabel Keluar: Tentukan variabel yang akan dikeluarkan dari basis. Ini dilakukan dengan menghitung rasio antara sisi kanan persamaan kendala dan koefisien variabel masuk dalam kolom yang sama. Variabel dengan rasio terkecil akan dikeluarkan.
- Pivot: Lakukan pivot pada elemen yang terletak pada persimpangan baris variabel keluar dan kolom variabel masuk. Ini akan mengubah tabel simplex dan menghasilkan solusi baru.
- Ulangi Langkah 3-5: Ulangi langkah 3-5 sampai solusi optimal ditemukan. Solusi optimal dicapai ketika semua koefisien dalam baris fungsi objektif adalah non-positif.
Contoh Soal Program Linear dan Penyelesaiannya dengan Metode Simplex
Sebuah perusahaan memproduksi dua jenis produk, A dan B. Setiap produk membutuhkan bahan baku dan waktu produksi seperti yang ditunjukkan dalam tabel berikut:
| Produk | Bahan Baku (kg) | Waktu Produksi (jam) |
|---|---|---|
| A | 2 | 3 |
| B | 3 | 2 |
Perusahaan memiliki 12 kg bahan baku dan 15 jam waktu produksi yang tersedia. Keuntungan per unit produk A adalah Rp. 50.000 dan keuntungan per unit produk B adalah Rp. 40.000. Berapakah jumlah produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan?
Rumusan Masalah:
* Misalkan x adalah jumlah produk A yang diproduksi dan y adalah jumlah produk B yang diproduksi.
* Fungsi objektif: Maksimalkan keuntungan Z = 50.000x + 40.000y
* Kendala:
* 2x + 3y ≤ 12 (Kendala bahan baku)
* 3x + 2y ≤ 15 (Kendala waktu produksi)
* x ≥ 0, y ≥ 0 (Kendala non-negatif)
Langkah-langkah Penyelesaian:
1. Bentuk Standar:
* Tambahkan variabel slack s1 dan s2 untuk kendala bahan baku dan waktu produksi, sehingga:
* 2x + 3y + s1 = 12
* 3x + 2y + s2 = 15
* Fungsi objektif: Z – 50.000x – 40.000y = 0
2. Buat Tabel Simplex:
| Variabel | x | y | s1 | s2 | Sisi Kanan |
|—|—|—|—|—|—|
| s1 | 2 | 3 | 1 | 0 | 12 |
| s2 | 3 | 2 | 0 | 1 | 15 |
| Z | -50.000 | -40.000 | 0 | 0 | 0 |
3. Pilih Variabel Masuk: Variabel x memiliki koefisien paling positif dalam baris fungsi objektif (-50.000), sehingga x dipilih sebagai variabel masuk.
4. Pilih Variabel Keluar: Hitung rasio antara sisi kanan persamaan kendala dan koefisien x dalam kolom yang sama:
* Untuk s1: 12/2 = 6
* Untuk s2: 15/3 = 5
* Variabel s2 memiliki rasio terkecil (5), sehingga s2 dipilih sebagai variabel keluar.
5. Pivot: Lakukan pivot pada elemen yang terletak pada persimpangan baris s2 dan kolom x (yaitu 3). Bagi setiap elemen dalam baris s2 dengan 3, dan kemudian gunakan operasi baris elementer untuk membuat semua elemen lain dalam kolom x menjadi 0.
| Variabel | x | y | s1 | s2 | Sisi Kanan |
|—|—|—|—|—|—|
| s1 | 0 | 5/3 | 1 | -2/3 | 2 |
| x | 1 | 2/3 | 0 | 1/3 | 5 |
| Z | 0 | -20.000 | 0 | 16.667 | 250.000 |
6. Ulangi Langkah 3-5: Variabel y memiliki koefisien paling positif dalam baris fungsi objektif (-20.000), sehingga y dipilih sebagai variabel masuk. Hitung rasio antara sisi kanan persamaan kendala dan koefisien y dalam kolom yang sama:
* Untuk s1: 2 / (5/3) = 1.2
* Untuk x: 5 / (2/3) = 7.5
* Variabel s1 memiliki rasio terkecil (1.2), sehingga s1 dipilih sebagai variabel keluar.
7. Pivot: Lakukan pivot pada elemen yang terletak pada persimpangan baris s1 dan kolom y (yaitu 5/3). Bagi setiap elemen dalam baris s1 dengan 5/3, dan kemudian gunakan operasi baris elementer untuk membuat semua elemen lain dalam kolom y menjadi 0.
| Variabel | x | y | s1 | s2 | Sisi Kanan |
|—|—|—|—|—|—|
| y | 0 | 1 | 3/5 | -2/5 | 1.2 |
| x | 1 | 0 | -2/5 | 1 | 4.4 |
| Z | 0 | 0 | 12.000 | 8.000 | 272.000 |
8. Solusi Optimal: Semua koefisien dalam baris fungsi objektif adalah non-positif, sehingga solusi optimal telah ditemukan. Solusi optimal adalah x = 4.4 dan y = 1.2, dengan keuntungan maksimum sebesar Rp. 272.000.
Tabel Simplex untuk Setiap Iterasi:
Iterasi 1:
| Variabel | x | y | s1 | s2 | Sisi Kanan |
|—|—|—|—|—|—|
| s1 | 2 | 3 | 1 | 0 | 12 |
| s2 | 3 | 2 | 0 | 1 | 15 |
| Z | -50.000 | -40.000 | 0 | 0 | 0 |
Iterasi 2:
| Variabel | x | y | s1 | s2 | Sisi Kanan |
|—|—|—|—|—|—|
| s1 | 0 | 5/3 | 1 | -2/3 | 2 |
| x | 1 | 2/3 | 0 | 1/3 | 5 |
| Z | 0 | -20.000 | 0 | 16.667 | 250.000 |
Iterasi 3:
| Variabel | x | y | s1 | s2 | Sisi Kanan |
|—|—|—|—|—|—|
| y | 0 | 1 | 3/5 | -2/5 | 1.2 |
| x | 1 | 0 | -2/5 | 1 | 4.4 |
| Z | 0 | 0 | 12.000 | 8.000 | 272.000 |
Perubahan Nilai Variabel dan Fungsi Objektif:
* Pada iterasi pertama, variabel x dimasukkan ke dalam basis dan variabel s2 dikeluarkan. Nilai x berubah dari 0 menjadi 5, dan nilai s2 berubah dari 15 menjadi 0. Nilai fungsi objektif meningkat dari 0 menjadi 250.000.
* Pada iterasi kedua, variabel y dimasukkan ke dalam basis dan variabel s1 dikeluarkan. Nilai y berubah dari 0 menjadi 1.2, dan nilai s1 berubah dari 2 menjadi 0. Nilai fungsi objektif meningkat dari 250.000 menjadi 272.000.
Kesimpulan:
Solusi optimal untuk masalah program linear ini adalah memproduksi 4.4 unit produk A dan 1.2 unit produk B, yang akan menghasilkan keuntungan maksimum sebesar Rp. 272.000.
Penerapan Program Linear
Program linear merupakan alat yang ampuh untuk menyelesaikan masalah pengoptimalan dalam berbagai bidang. Dengan menggunakan program linear, kita dapat menentukan cara terbaik untuk mengalokasikan sumber daya terbatas untuk mencapai tujuan tertentu, seperti memaksimalkan keuntungan atau meminimalkan biaya.
Penerapan Program Linear dalam Berbagai Bidang
Program linear memiliki aplikasi yang luas dalam berbagai bidang, termasuk:
- Ekonomi: Program linear dapat digunakan untuk memodelkan masalah ekonomi seperti alokasi sumber daya, perencanaan produksi, dan perdagangan internasional.
- Bisnis: Dalam bisnis, program linear dapat digunakan untuk mengoptimalkan proses produksi, menentukan strategi pemasaran terbaik, dan mengelola inventaris.
- Industri: Program linear dapat digunakan untuk memaksimalkan efisiensi produksi, mengoptimalkan penggunaan energi, dan meminimalkan biaya produksi.
Memaksimalkan Keuntungan dan Meminimalkan Biaya
Program linear dapat digunakan untuk memaksimalkan keuntungan atau meminimalkan biaya dengan menentukan kombinasi optimal dari variabel keputusan yang memenuhi kendala tertentu.
- Memaksimalkan Keuntungan: Dalam bisnis, program linear dapat digunakan untuk menentukan jumlah produk yang harus diproduksi untuk memaksimalkan keuntungan, dengan mempertimbangkan kendala seperti ketersediaan bahan baku, kapasitas produksi, dan permintaan pasar.
- Meminimalkan Biaya: Program linear dapat digunakan untuk menentukan cara paling efisien untuk mengalokasikan sumber daya untuk meminimalkan biaya produksi, dengan mempertimbangkan kendala seperti ketersediaan tenaga kerja, bahan baku, dan biaya transportasi.
Contoh Kasus Program Linear yang Lebih Kompleks
Berikut adalah contoh kasus program linear yang melibatkan kendala dan fungsi objektif yang lebih kompleks:
Sebuah perusahaan manufaktur memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku, sedangkan produk B membutuhkan 3 jam waktu produksi dan 2 kg bahan baku. Perusahaan memiliki 100 jam waktu produksi dan 50 kg bahan baku yang tersedia. Keuntungan dari produk A adalah Rp10.000 per unit, sedangkan keuntungan dari produk B adalah Rp15.000 per unit. Berapa banyak unit produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan?
Dalam kasus ini, fungsi objektif adalah memaksimalkan keuntungan, yang merupakan fungsi linear dari jumlah unit produk A dan B yang diproduksi. Kendala dalam kasus ini adalah ketersediaan waktu produksi dan bahan baku. Dengan menggunakan program linear, kita dapat menentukan kombinasi optimal dari jumlah unit produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan, dengan mempertimbangkan kendala yang ada.
Soal Latihan
Berikut ini adalah 5 contoh soal program linear dengan berbagai tingkat kesulitan. Soal-soal ini dirancang untuk membantu kamu memahami konsep dasar program linear dan mengasah kemampuan dalam menyelesaikan masalah optimasi.
Soal Mudah
Soal-soal mudah ini akan membantu kamu memahami konsep dasar program linear dan cara menyelesaikan masalah optimasi sederhana.
- Seorang tukang roti membuat dua jenis kue, yaitu kue A dan kue B. Kue A membutuhkan 2 kg tepung dan 1 kg gula, sedangkan kue B membutuhkan 1 kg tepung dan 2 kg gula. Tukang roti memiliki 10 kg tepung dan 8 kg gula. Jika keuntungan dari kue A adalah Rp 5.000,- per kue dan keuntungan dari kue B adalah Rp 4.000,- per kue, berapa banyak kue A dan kue B yang harus dibuat agar keuntungan maksimum?
- Sebuah perusahaan memproduksi dua jenis produk, yaitu produk X dan produk Y. Produk X membutuhkan 3 jam waktu produksi dan 2 kg bahan baku, sedangkan produk Y membutuhkan 2 jam waktu produksi dan 1 kg bahan baku. Perusahaan memiliki 12 jam waktu produksi dan 8 kg bahan baku. Jika keuntungan dari produk X adalah Rp 10.000,- per unit dan keuntungan dari produk Y adalah Rp 8.000,- per unit, berapa banyak produk X dan produk Y yang harus diproduksi agar keuntungan maksimum?
Soal Sedang
Soal-soal sedang ini akan menguji pemahaman kamu tentang program linear dalam situasi yang lebih kompleks. Soal-soal ini membutuhkan pemikiran kritis dan kemampuan dalam merumuskan model matematika yang tepat.
- Sebuah perusahaan manufaktur memproduksi dua jenis produk, yaitu produk A dan produk B. Produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku, sedangkan produk B membutuhkan 1 jam waktu produksi dan 2 kg bahan baku. Perusahaan memiliki 10 jam waktu produksi dan 8 kg bahan baku. Jika keuntungan dari produk A adalah Rp 15.000,- per unit dan keuntungan dari produk B adalah Rp 10.000,- per unit, berapa banyak produk A dan produk B yang harus diproduksi agar keuntungan maksimum? Selain itu, perusahaan juga memiliki batasan produksi, yaitu tidak boleh memproduksi lebih dari 5 unit produk A dan 4 unit produk B.
- Sebuah perusahaan makanan memproduksi dua jenis makanan ringan, yaitu makanan ringan X dan makanan ringan Y. Makanan ringan X membutuhkan 1 kg bahan baku A dan 2 kg bahan baku B, sedangkan makanan ringan Y membutuhkan 2 kg bahan baku A dan 1 kg bahan baku B. Perusahaan memiliki 10 kg bahan baku A dan 8 kg bahan baku B. Jika keuntungan dari makanan ringan X adalah Rp 8.000,- per unit dan keuntungan dari makanan ringan Y adalah Rp 10.000,- per unit, berapa banyak makanan ringan X dan makanan ringan Y yang harus diproduksi agar keuntungan maksimum? Perusahaan juga memiliki batasan produksi, yaitu tidak boleh memproduksi lebih dari 3 unit makanan ringan X dan 4 unit makanan ringan Y.
Soal Sulit
Soal-soal sulit ini akan menguji kemampuan kamu dalam menyelesaikan masalah optimasi yang lebih kompleks dengan berbagai batasan dan persyaratan.
- Sebuah perusahaan penerbangan memiliki dua jenis pesawat, yaitu pesawat A dan pesawat B. Pesawat A dapat mengangkut 100 penumpang dan membutuhkan 1.000 liter bahan bakar per jam, sedangkan pesawat B dapat mengangkut 200 penumpang dan membutuhkan 1.500 liter bahan bakar per jam. Perusahaan memiliki 10.000 liter bahan bakar dan ingin mengangkut 1.000 penumpang. Berapa banyak pesawat A dan pesawat B yang harus digunakan agar biaya bahan bakar minimum? Selain itu, perusahaan juga memiliki batasan penggunaan pesawat, yaitu tidak boleh menggunakan lebih dari 5 pesawat A dan 3 pesawat B.
- Sebuah perusahaan manufaktur memproduksi dua jenis produk, yaitu produk X dan produk Y. Produk X membutuhkan 2 jam waktu produksi dan 1 kg bahan baku, sedangkan produk Y membutuhkan 1 jam waktu produksi dan 2 kg bahan baku. Perusahaan memiliki 10 jam waktu produksi dan 8 kg bahan baku. Jika keuntungan dari produk X adalah Rp 15.000,- per unit dan keuntungan dari produk Y adalah Rp 10.000,- per unit, berapa banyak produk X dan produk Y yang harus diproduksi agar keuntungan maksimum? Perusahaan juga memiliki batasan produksi, yaitu tidak boleh memproduksi lebih dari 5 unit produk X dan 4 unit produk Y. Selain itu, perusahaan juga memiliki batasan penggunaan tenaga kerja, yaitu tidak boleh menggunakan lebih dari 10 jam kerja untuk memproduksi kedua produk tersebut.
Ilustrasi Grafik
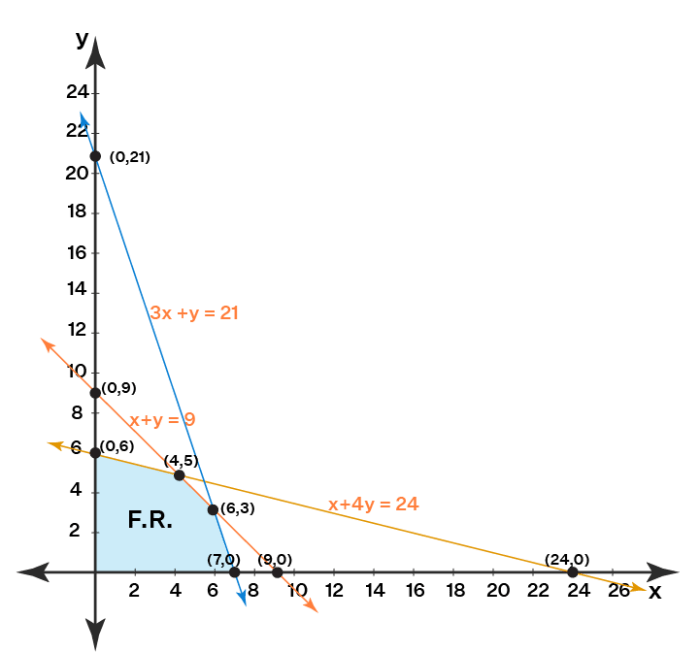
Metode grafik merupakan salah satu cara untuk menyelesaikan program linear. Metode ini menggunakan grafik untuk menggambarkan batasan dari kendala dan mencari titik optimal dari fungsi objektif.
Langkah-Langkah Metode Grafik
- Gambarlah garis yang mewakili setiap kendala pada grafik.
- Tentukan daerah yang memenuhi semua kendala (daerah feasible).
- Tentukan titik-titik sudut dari daerah feasible.
- Evaluasi fungsi objektif pada setiap titik sudut.
- Titik sudut yang menghasilkan nilai optimal dari fungsi objektif merupakan solusi optimal dari program linear.
Contoh Ilustrasi Grafik
Misalnya, kita memiliki program linear berikut:
Maximalkan Z = 2x + 3y
dengan kendala:
x + y ≤ 5
2x + y ≤ 8
x ≥ 0
y ≥ 0
Berikut adalah langkah-langkah untuk menyelesaikan program linear tersebut dengan metode grafik:
- Gambarlah garis yang mewakili setiap kendala pada grafik.
– x + y = 5
– 2x + y = 8
– x = 0
– y = 0 - Tentukan daerah yang memenuhi semua kendala (daerah feasible).
Daerah feasible adalah daerah yang terletak di bawah garis x + y = 5, di bawah garis 2x + y = 8, di kanan garis x = 0, dan di atas garis y = 0. - Tentukan titik-titik sudut dari daerah feasible.
Titik-titik sudut dari daerah feasible adalah (0,0), (0,5), (4,1), dan (8,0). - Evaluasi fungsi objektif pada setiap titik sudut.
– Z(0,0) = 2(0) + 3(0) = 0
– Z(0,5) = 2(0) + 3(5) = 15
– Z(4,1) = 2(4) + 3(1) = 11
– Z(8,0) = 2(8) + 3(0) = 16 - Titik sudut yang menghasilkan nilai optimal dari fungsi objektif merupakan solusi optimal dari program linear.
Titik sudut (8,0) menghasilkan nilai Z yang maksimal, yaitu 16. Jadi, solusi optimal dari program linear ini adalah x = 8 dan y = 0.
Berikut adalah yang menunjukkan titik-titik sudut dari daerah feasible dan nilai fungsi objektif pada setiap titik:
| Titik Sudut | x | y | Z = 2x + 3y |
|---|---|---|---|
| (0,0) | 0 | 0 | 0 |
| (0,5) | 0 | 5 | 15 |
| (4,1) | 4 | 1 | 11 |
| (8,0) | 8 | 0 | 16 |
Penutup
Metode grafik merupakan cara yang mudah dan intuitif untuk menyelesaikan program linear. Dengan menggunakan grafik, kita dapat dengan mudah melihat batasan dari kendala dan mencari titik optimal dari fungsi objektif.
Contoh Penerapan dalam Bisnis
Program linear memiliki aplikasi yang luas dalam dunia bisnis, terutama dalam pengambilan keputusan yang melibatkan optimalisasi sumber daya. Dalam berbagai situasi, program linear dapat membantu perusahaan untuk memaksimalkan keuntungan, meminimalkan biaya, atau menentukan strategi produksi yang paling efisien.
Menentukan Strategi Produksi Optimal
Program linear dapat digunakan untuk menentukan strategi produksi optimal yang memaksimalkan keuntungan dengan mempertimbangkan kendala sumber daya yang tersedia. Misalnya, perusahaan manufaktur yang memproduksi dua jenis produk, A dan B, ingin mengetahui berapa banyak unit dari masing-masing produk yang harus diproduksi untuk mencapai keuntungan maksimum.
Misalkan perusahaan memiliki 100 jam tenaga kerja dan 200 kg bahan baku. Setiap unit produk A membutuhkan 2 jam tenaga kerja dan 3 kg bahan baku, sementara setiap unit produk B membutuhkan 3 jam tenaga kerja dan 2 kg bahan baku. Keuntungan per unit produk A adalah Rp10.000 dan per unit produk B adalah Rp15.000.
Dengan menggunakan program linear, perusahaan dapat merumuskan model matematika yang memaksimalkan keuntungan dengan mempertimbangkan kendala tenaga kerja dan bahan baku. Model ini dapat diselesaikan dengan menggunakan metode Simplex atau metode grafik untuk menentukan jumlah optimal produk A dan B yang harus diproduksi.
Membantu Perusahaan dalam Pengambilan Keputusan
Program linear memberikan kerangka kerja yang sistematis untuk menganalisis masalah optimasi dalam bisnis. Berikut adalah beberapa cara program linear dapat membantu perusahaan dalam pengambilan keputusan:
- Menentukan alokasi sumber daya yang optimal: Program linear membantu perusahaan untuk menentukan cara terbaik mengalokasikan sumber daya yang terbatas, seperti tenaga kerja, bahan baku, dan modal, untuk memaksimalkan keuntungan atau meminimalkan biaya.
- Membuat rencana produksi yang efisien: Program linear membantu perusahaan untuk merencanakan produksi yang efisien dengan mempertimbangkan permintaan pasar, ketersediaan bahan baku, dan kapasitas produksi.
- Membuat keputusan investasi yang strategis: Program linear dapat membantu perusahaan dalam memilih investasi yang paling menguntungkan dengan mempertimbangkan faktor-faktor seperti pengembalian investasi, risiko, dan jangka waktu investasi.
- Mengoptimalkan rantai pasokan: Program linear dapat digunakan untuk mengoptimalkan rantai pasokan dengan menentukan rute pengiriman yang paling efisien, mengelola inventaris, dan meminimalkan biaya transportasi.
Contoh Penerapan dalam Industri: Contoh Soal Program Linear Dan Penyelesaiannya
Program linear memiliki aplikasi luas di berbagai industri, membantu perusahaan dalam pengambilan keputusan yang optimal untuk meningkatkan efisiensi dan memaksimalkan keuntungan. Salah satu contoh penerapannya adalah dalam menentukan alokasi sumber daya yang optimal untuk meminimalkan biaya produksi.
Alokasi Sumber Daya Optimal
Program linear dapat membantu perusahaan dalam menentukan cara terbaik untuk mengalokasikan sumber daya yang terbatas, seperti tenaga kerja, bahan baku, dan mesin, untuk menghasilkan produk atau layanan tertentu. Dengan memodelkan kendala dan tujuan perusahaan dalam bentuk persamaan linear, program linear dapat menghasilkan solusi optimal yang meminimalkan biaya produksi atau memaksimalkan keuntungan.
Berikut adalah contoh kasus dalam industri manufaktur:
| Produk | Keuntungan per Unit (Rp) | Waktu Produksi per Unit (Jam) | Bahan Baku per Unit (Kg) |
|---|---|---|---|
| A | 100.000 | 2 | 5 |
| B | 150.000 | 3 | 3 |
Perusahaan memiliki kapasitas produksi maksimal 100 jam dan bahan baku tersedia sebanyak 200 kg.
Dengan menggunakan program linear, perusahaan dapat menentukan jumlah optimal produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan. Model program linearnya dapat dirumuskan sebagai berikut:
Membuat fungsi objektif (tujuan): Memaksimalkan keuntungan (Z) = 100.000A + 150.000B
Menentukan kendala:
– Waktu produksi: 2A + 3B ≤ 100
– Bahan baku: 5A + 3B ≤ 200
– Non-negatif: A ≥ 0, B ≥ 0
Dengan menggunakan metode Simplex atau metode grafik, perusahaan dapat menemukan solusi optimal yang menghasilkan keuntungan maksimum.
Contoh Soal dan Penyelesaian
Program linear adalah salah satu alat penting dalam matematika yang dapat membantu kita dalam menyelesaikan masalah optimasi. Masalah optimasi ini melibatkan mencari nilai optimal (maksimum atau minimum) dari suatu fungsi objektif, dengan batasan-batasan tertentu yang disebut kendala.
Berikut ini adalah contoh soal program linear yang melibatkan kendala dan fungsi objektif yang lebih kompleks, serta penyelesaiannya dengan metode simplex.
Contoh Soal Program Linear
Sebuah perusahaan memproduksi dua jenis produk, yaitu produk A dan produk B. Setiap produk memerlukan bahan baku dan waktu produksi yang berbeda. Data tentang bahan baku, waktu produksi, dan keuntungan per unit produk ditunjukkan pada tabel berikut:
| Produk | Bahan Baku (Kg) | Waktu Produksi (Jam) | Keuntungan (Rp) |
|---|---|---|---|
| A | 2 | 3 | 10.000 |
| B | 3 | 2 | 15.000 |
Perusahaan memiliki ketersediaan bahan baku sebanyak 60 kg dan waktu produksi maksimal 60 jam. Berapa unit produk A dan produk B yang harus diproduksi agar keuntungan maksimal?
Contoh soal program linear dan penyelesaiannya biasanya melibatkan masalah optimasi, seperti menentukan jumlah produksi maksimum dengan batasan sumber daya. Nah, untuk menyelesaikannya, kita perlu memahami konsep-konsep seperti fungsi objektif dan kendala. Ada banyak metode yang bisa digunakan, seperti metode grafik dan metode simplex.
Nah, konsep dilatasi dalam transformasi geometri juga bisa diterapkan dalam program linear, misalnya untuk memperbesar atau memperkecil area suatu wilayah produksi. Untuk memahami lebih lanjut tentang dilatasi, kamu bisa cek contoh soal dilatasi transformasi geometri. Kembali ke program linear, memahami konsep-konsep tersebut akan memudahkanmu dalam menyelesaikan soal-soal dan menemukan solusi optimal untuk masalah yang diberikan.
Penyelesaian dengan Metode Simplex
Langkah-langkah penyelesaian dengan metode simplex adalah sebagai berikut:
- Menentukan Fungsi Objektif dan Kendala
- 2x + 3y ≤ 60 (Kendala bahan baku)
- 3x + 2y ≤ 60 (Kendala waktu produksi)
- x ≥ 0 (Jumlah produk A tidak boleh negatif)
- y ≥ 0 (Jumlah produk B tidak boleh negatif)
- Membuat Tabel Simplex
- Kolom Variabel Basis:
- Kolom Koefisien Fungsi Objektif:
- Kolom Solusi:
- Kolom Kendala:
- S1 dan S2 adalah variabel slack, yang ditambahkan untuk mengubah pertidaksamaan kendala menjadi persamaan.
- Koefisien fungsi objektif untuk variabel basis (Z) adalah 1, sedangkan untuk variabel lainnya adalah negatif dari koefisiennya dalam fungsi objektif.
- Solusi awal adalah nilai variabel slack yang memenuhi kendala.
- Menentukan Variabel Masuk
- Menentukan Variabel Keluar
- Melakukan Iterasi Simplex
- Membuat elemen pivot menjadi 1 dengan membagi baris pivot dengan nilai elemen pivot.
- Membuat elemen lain pada kolom variabel masuk menjadi 0 dengan melakukan operasi baris elementer.
- Interpretasi Solusi
Fungsi objektif adalah fungsi yang ingin kita optimalkan, dalam hal ini adalah keuntungan. Misalkan x adalah jumlah produk A dan y adalah jumlah produk B, maka fungsi objektifnya adalah:
Z = 10.000x + 15.000y
Kendala adalah batasan-batasan yang harus dipenuhi, dalam hal ini adalah ketersediaan bahan baku dan waktu produksi. Kendala dapat dirumuskan sebagai berikut:
Tabel simplex adalah tabel yang digunakan untuk menyelesaikan masalah program linear dengan metode simplex. Tabel simplex terdiri dari beberapa kolom, yaitu:
Tabel simplex awal untuk soal ini adalah:
| Variabel Basis | Z | x | y | S1 | S2 | Solusi |
|---|---|---|---|---|---|---|
| Z | 1 | -10.000 | -15.000 | 0 | 0 | 0 |
| S1 | 0 | 2 | 3 | 1 | 0 | 60 |
| S2 | 0 | 3 | 2 | 0 | 1 | 60 |
Keterangan:
Variabel masuk adalah variabel yang akan dimasukkan ke dalam basis pada iterasi berikutnya. Variabel masuk dipilih dari variabel non-basis yang memiliki koefisien negatif terbesar dalam baris Z. Dalam tabel simplex awal, variabel masuk adalah y, karena memiliki koefisien negatif terbesar (-15.000).
Variabel keluar adalah variabel yang akan dikeluarkan dari basis pada iterasi berikutnya. Variabel keluar dipilih dari variabel basis yang memiliki rasio terkecil antara nilai solusi dan koefisien variabel masuk pada kolom kendala. Dalam tabel simplex awal, variabel keluar adalah S1, karena memiliki rasio terkecil (60/3 = 20).
Iterasi simplex dilakukan dengan mengubah tabel simplex dengan cara:
Iterasi pertama menghasilkan tabel simplex berikut:
| Variabel Basis | Z | x | y | S1 | S2 | Solusi |
|---|---|---|---|---|---|---|
| Z | 1 | -2.500 | 0 | 5.000 | 0 | 300.000 |
| y | 0 | 2/3 | 1 | 1/3 | 0 | 20 |
| S2 | 0 | 5/3 | 0 | -2/3 | 1 | 20 |
Iterasi kedua menghasilkan tabel simplex berikut:
| Variabel Basis | Z | x | y | S1 | S2 | Solusi |
|---|---|---|---|---|---|---|
| Z | 1 | 0 | 0 | 4.000 | 1.000 | 320.000 |
| y | 0 | 0 | 1 | 1/2 | -1/5 | 16 |
| x | 0 | 1 | 0 | -2/5 | 3/5 | 12 |
Tabel simplex terakhir menunjukkan bahwa solusi optimal telah tercapai. Solusi optimal adalah x = 12 dan y = 16, dengan keuntungan maksimal Z = 320.000.
Solusi optimal menunjukkan bahwa perusahaan harus memproduksi 12 unit produk A dan 16 unit produk B untuk mencapai keuntungan maksimal sebesar 320.000.
Contoh Soal dengan Ilustrasi
Program linear sering kali melibatkan kendala dan fungsi objektif yang lebih kompleks. Dalam contoh ini, kita akan menganalisis sebuah kasus yang mendemonstrasikan bagaimana menyelesaikan masalah program linear dengan metode grafik, sambil menunjukkan langkah-langkahnya secara detail.
Contoh Soal
Sebuah perusahaan memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 kg bahan baku per unit, sedangkan produk B membutuhkan 3 jam waktu produksi dan 2 kg bahan baku per unit. Perusahaan memiliki 120 jam waktu produksi dan 60 kg bahan baku yang tersedia setiap hari. Keuntungan per unit produk A adalah Rp. 10.000 dan per unit produk B adalah Rp. 15.000. Berapa banyak unit produk A dan B yang harus diproduksi setiap hari untuk memaksimalkan keuntungan?
Langkah-langkah Penyelesaian dengan Metode Grafik
- Menetapkan Variabel:
- Misalkan x adalah jumlah unit produk A yang diproduksi.
- Misalkan y adalah jumlah unit produk B yang diproduksi.
- Menentukan Fungsi Objektif:
- Fungsi objektif yang ingin dimaksimalkan adalah keuntungan total, yaitu Z = 10.000x + 15.000y.
- Menentukan Kendala:
- Kendala waktu produksi: 2x + 3y ≤ 120.
- Kendala bahan baku: x + 2y ≤ 60.
- Kendala non-negatif: x ≥ 0 dan y ≥ 0.
- Menggambar Grafik:
- Gambar garis yang mewakili kendala waktu produksi (2x + 3y = 120) dan kendala bahan baku (x + 2y = 60) pada bidang koordinat x-y.
- Tentukan daerah yang memenuhi semua kendala (daerah yang diarsir). Daerah ini disebut daerah layak.
- Menentukan Titik-titik Sudut:
- Tentukan titik-titik sudut daerah layak. Titik-titik ini adalah titik potong garis-garis yang mewakili kendala.
- Menghitung Nilai Fungsi Objektif:
- Hitung nilai fungsi objektif (Z = 10.000x + 15.000y) pada setiap titik sudut daerah layak.
- Menentukan Solusi Optimal:
- Titik sudut yang menghasilkan nilai fungsi objektif maksimum adalah solusi optimal.
Ilustrasi Grafik
| Titik Sudut | Koordinat (x, y) | Nilai Fungsi Objektif (Z) |
|---|---|---|
| O | (0, 0) | 0 |
| A | (0, 20) | 300.000 |
| B | (30, 15) | 450.000 |
| C | (60, 0) | 600.000 |
Dari tabel di atas, terlihat bahwa titik sudut B (30, 15) menghasilkan nilai fungsi objektif maksimum, yaitu Rp. 450.000. Oleh karena itu, solusi optimalnya adalah memproduksi 30 unit produk A dan 15 unit produk B setiap hari untuk memaksimalkan keuntungan.
Penutup
Dengan memahami konsep program linear dan berbagai metode penyelesaiannya, Anda dapat menerapkannya untuk menyelesaikan masalah optimasi yang kompleks dalam berbagai bidang. Melalui contoh soal dan ilustrasi yang diberikan, diharapkan Anda dapat memperoleh pemahaman yang lebih dalam tentang program linear dan kemampuannya dalam membantu pengambilan keputusan yang efektif.




