Contoh Soal Refleksi Matematika Kelas 11: Uji Kemampuanmu!

Contoh soal refleksi matematika kelas 11 – Pernahkah kamu memperhatikan pantulan bayanganmu di cermin? Atau mungkin kamu pernah mengamati bagaimana sebuah objek tampak berbeda saat dipantulkan pada permukaan air? Nah, itulah contoh konkret dari konsep refleksi dalam matematika! Refleksi merupakan salah satu transformasi geometri yang mempelajari bagaimana suatu objek dapat dipindahkan atau diubah bentuknya melalui pencerminan.

Di kelas 11, kamu akan mempelajari lebih dalam tentang refleksi, mulai dari pengertian, jenis-jenis, rumus, hingga aplikasinya dalam kehidupan sehari-hari. Untuk menguji pemahamanmu, berikut ini beberapa contoh soal refleksi matematika kelas 11 yang bisa kamu coba kerjakan.

Pengertian Refleksi

Refleksi dalam matematika merupakan transformasi geometri yang menghasilkan bayangan suatu objek terhadap suatu garis atau bidang. Bayangan tersebut memiliki bentuk dan ukuran yang sama dengan objek aslinya, tetapi berada di sisi yang berlawanan dari garis atau bidang refleksi.

Contoh Refleksi dalam Kehidupan Sehari-hari

Refleksi dapat ditemukan dalam berbagai situasi sehari-hari. Berikut beberapa contohnya:

• Cermin: Saat kita bercermin, kita melihat bayangan diri kita yang merupakan hasil refleksi terhadap permukaan cermin.
• Air Tergenang: Saat melihat ke permukaan air yang tenang, kita melihat bayangan benda di atasnya. Bayangan ini terbentuk karena cahaya yang dipantulkan dari benda tersebut mengalami refleksi pada permukaan air.
• Foto: Foto merupakan hasil refleksi objek nyata terhadap lensa kamera.

Sifat-Sifat Refleksi

Refleksi memiliki beberapa sifat penting, yaitu:

• Menjaga Bentuk dan Ukuran: Refleksi tidak mengubah bentuk dan ukuran objek, hanya memindahkannya ke lokasi yang berbeda.
• Membalikkan Orientasi: Refleksi membalikkan orientasi objek, yaitu mengubah arah objek. Misalnya, jika objek asli berputar searah jarum jam, bayangannya akan berputar berlawanan arah jarum jam.
• Memiliki Garis atau Bidang Refleksi: Setiap refleksi memiliki garis atau bidang refleksi yang merupakan sumbu simetri antara objek asli dan bayangannya.

Jenis-Jenis Refleksi

Refleksi dalam matematika merupakan transformasi geometri yang menghasilkan bayangan suatu objek terhadap sebuah garis, yang disebut sumbu refleksi. Bayangan yang dihasilkan akan memiliki bentuk dan ukuran yang sama dengan objek aslinya, namun memiliki orientasi yang berlawanan. Ada beberapa jenis refleksi berdasarkan sumbu refleksinya, yang akan dibahas lebih lanjut di bawah ini.

Refleksi terhadap Sumbu-X

Refleksi terhadap sumbu-x merupakan transformasi yang menghasilkan bayangan suatu objek terhadap sumbu-x. Untuk melakukan refleksi terhadap sumbu-x, kita dapat menggunakan rumus berikut:

(x, y) → (x, -y)

Contoh soal:
Tentukan bayangan titik A(2, 3) setelah direfleksikan terhadap sumbu-x.
Penyelesaian:
Dengan menggunakan rumus di atas, bayangan titik A(2, 3) setelah direfleksikan terhadap sumbu-x adalah A'(2, -3).

Refleksi terhadap Sumbu-Y

Refleksi terhadap sumbu-y merupakan transformasi yang menghasilkan bayangan suatu objek terhadap sumbu-y. Untuk melakukan refleksi terhadap sumbu-y, kita dapat menggunakan rumus berikut:

(x, y) → (-x, y)

Contoh soal:
Tentukan bayangan titik B(-1, 4) setelah direfleksikan terhadap sumbu-y.
Penyelesaian:
Dengan menggunakan rumus di atas, bayangan titik B(-1, 4) setelah direfleksikan terhadap sumbu-y adalah B'(1, 4).

Refleksi terhadap Garis y = x

Refleksi terhadap garis y = x merupakan transformasi yang menghasilkan bayangan suatu objek terhadap garis y = x. Untuk melakukan refleksi terhadap garis y = x, kita dapat menggunakan rumus berikut:

(x, y) → (y, x)

Contoh soal:
Tentukan bayangan titik C(5, 1) setelah direfleksikan terhadap garis y = x.
Penyelesaian:
Dengan menggunakan rumus di atas, bayangan titik C(5, 1) setelah direfleksikan terhadap garis y = x adalah C'(1, 5).

Refleksi terhadap Garis y = -x, Contoh soal refleksi matematika kelas 11

Refleksi terhadap garis y = -x merupakan transformasi yang menghasilkan bayangan suatu objek terhadap garis y = -x. Untuk melakukan refleksi terhadap garis y = -x, kita dapat menggunakan rumus berikut:

(x, y) → (-y, -x)

Contoh soal:
Tentukan bayangan titik D(-3, -2) setelah direfleksikan terhadap garis y = -x.
Penyelesaian:
Dengan menggunakan rumus di atas, bayangan titik D(-3, -2) setelah direfleksikan terhadap garis y = -x adalah D'(2, 3).

Tabel Jenis Refleksi

Jenis Refleksi	Sumbu Refleksi	Contoh Gambar
Refleksi terhadap sumbu-x	Sumbu-x	Gambar: Titik A(2, 3) direfleksikan terhadap sumbu-x menghasilkan A'(2, -3).
Refleksi terhadap sumbu-y	Sumbu-y	Gambar: Titik B(-1, 4) direfleksikan terhadap sumbu-y menghasilkan B'(1, 4).
Refleksi terhadap garis y = x	Garis y = x	Gambar: Titik C(5, 1) direfleksikan terhadap garis y = x menghasilkan C'(1, 5).
Refleksi terhadap garis y = -x	Garis y = -x	Gambar: Titik D(-3, -2) direfleksikan terhadap garis y = -x menghasilkan D'(2, 3).

Rumus Refleksi

Refleksi merupakan transformasi geometri yang menghasilkan bayangan suatu objek dengan cara “mencerminkan” objek tersebut terhadap suatu garis atau bidang. Garis atau bidang tersebut disebut sebagai sumbu refleksi. Pada dasarnya, refleksi dapat diartikan sebagai “mencerminkan” suatu objek terhadap sebuah garis atau bidang.

Rumus Umum Refleksi

Rumus umum untuk refleksi terhadap sumbu x, sumbu y, dan garis y = x dapat dirumuskan sebagai berikut:

• Refleksi terhadap sumbu x: (x, y) → (x, -y)
• Refleksi terhadap sumbu y: (x, y) → (-x, y)
• Refleksi terhadap garis y = x: (x, y) → (y, x)

Rumus-rumus ini dapat digunakan untuk menentukan bayangan titik setelah direfleksikan terhadap sumbu x, sumbu y, atau garis y = x.

Contoh Soal Refleksi

Misalkan kita ingin mencari bayangan titik A(2, 3) setelah direfleksikan terhadap sumbu x.

Berdasarkan rumus refleksi terhadap sumbu x, yaitu (x, y) → (x, -y), maka bayangan titik A(2, 3) adalah A'(2, -3).

Cara Menggunakan Rumus Refleksi

Untuk menggunakan rumus refleksi, Anda dapat mengikuti langkah-langkah berikut:

1. Tentukan sumbu refleksi.
2. Tentukan koordinat titik yang akan direfleksikan.
3. Gunakan rumus refleksi yang sesuai dengan sumbu refleksi.
4. Tentukan koordinat bayangan titik.

Dengan mengikuti langkah-langkah ini, Anda dapat dengan mudah menentukan bayangan titik setelah direfleksikan terhadap sumbu x, sumbu y, atau garis y = x.

Aplikasi Refleksi dalam Kehidupan Sehari-hari

Refleksi, dalam matematika, adalah transformasi geometri yang menghasilkan bayangan cermin dari suatu objek. Bayangan ini memiliki jarak yang sama dengan objek aslinya terhadap garis cermin atau sumbu refleksi. Konsep refleksi ini tidak hanya penting dalam matematika, tetapi juga memiliki aplikasi yang luas dalam kehidupan sehari-hari. Berikut ini adalah beberapa contohnya:

Seni dan Desain

Refleksi memiliki peran penting dalam seni dan desain. Seniman menggunakan refleksi untuk menciptakan efek visual yang menarik dan untuk menambahkan kedalaman dan dimensi pada karya mereka. Salah satu contohnya adalah penggunaan refleksi dalam lukisan. Seniman dapat menggunakan refleksi untuk menciptakan efek air yang berkilauan atau untuk menunjukkan bayangan objek di permukaan yang mengkilap.

• Perspektif: Refleksi membantu seniman dalam menciptakan perspektif yang realistis dalam lukisan. Dengan memahami bagaimana objek tercermin, seniman dapat menggambarkan kedalaman dan ruang dalam karya mereka.
• Komposisi: Refleksi dapat digunakan untuk menyeimbangkan komposisi dalam karya seni. Seniman dapat menggunakan refleksi untuk menciptakan simetri atau asimetri dalam karya mereka.
• Estetika: Refleksi dapat digunakan untuk meningkatkan estetika karya seni. Refleksi dapat menciptakan efek visual yang menarik dan memikat, seperti efek air yang berkilauan atau bayangan yang lembut.

Arsitektur dan Konstruksi

Dalam arsitektur dan konstruksi, refleksi digunakan dalam berbagai cara. Contohnya, arsitek dapat menggunakan refleksi untuk merancang bangunan yang simetris, seperti bangunan dengan fasad yang sama di kedua sisi. Refleksi juga digunakan dalam perencanaan dan desain bangunan untuk memastikan bahwa semua bagian bangunan memiliki proporsi yang tepat dan terhubung dengan baik.

• Simetri: Refleksi dapat digunakan untuk menciptakan simetri dalam desain bangunan. Contohnya, bangunan dengan fasad yang sama di kedua sisi dapat dirancang dengan menggunakan refleksi.
• Perencanaan: Refleksi digunakan dalam perencanaan dan desain bangunan untuk memastikan bahwa semua bagian bangunan memiliki proporsi yang tepat dan terhubung dengan baik. Contohnya, arsitek dapat menggunakan refleksi untuk memastikan bahwa semua jendela dan pintu pada sebuah bangunan berada pada ketinggian yang sama.
• Struktur: Refleksi juga digunakan dalam desain struktur bangunan. Contohnya, refleksi dapat digunakan untuk memastikan bahwa balok dan kolom dalam sebuah bangunan memiliki kekuatan yang cukup untuk menahan beban.

Fotografi dan Videografi

Dalam fotografi dan videografi, refleksi digunakan untuk menciptakan efek visual yang menarik. Fotografer dan videografer dapat menggunakan refleksi untuk menciptakan efek yang menarik, seperti refleksi air atau permukaan yang mengkilap. Refleksi juga dapat digunakan untuk menambahkan kedalaman dan dimensi pada gambar.

• Komposisi: Refleksi dapat digunakan untuk menyeimbangkan komposisi dalam foto dan video. Fotografer dan videografer dapat menggunakan refleksi untuk menciptakan simetri atau asimetri dalam karya mereka.
• Efek Visual: Refleksi dapat digunakan untuk menciptakan efek visual yang menarik dalam foto dan video. Contohnya, fotografer dapat menggunakan refleksi untuk menciptakan efek air yang berkilauan atau untuk menunjukkan bayangan objek di permukaan yang mengkilap.
• Kedalaman: Refleksi dapat digunakan untuk menambahkan kedalaman dan dimensi pada foto dan video. Refleksi dapat membuat gambar tampak lebih realistis dan menarik.

Contoh Soal Refleksi

Refleksi merupakan salah satu transformasi geometri yang melibatkan pencerminan suatu titik atau bangun terhadap suatu garis atau bidang. Konsep ini menarik karena dapat diterapkan dalam berbagai situasi, seperti dalam seni, desain, dan bahkan dalam bidang teknologi. Dalam mempelajari refleksi, penting untuk memahami konsep jarak, sudut, dan sifat-sifat refleksi. Untuk menguji pemahaman tersebut, berikut beberapa contoh soal refleksi yang dapat membantu kamu memahami konsep tersebut lebih dalam.

Soal Cerita tentang Refleksi

Soal cerita dapat membantu kamu memahami konsep refleksi dalam konteks yang lebih nyata. Soal cerita ini melibatkan konsep jarak dan sudut, yang dapat membantu kamu memvisualisasikan proses refleksi.

• Sebuah kapal pesiar berlayar dari pelabuhan A menuju pelabuhan B yang berada di seberang sebuah pulau. Kapal tersebut harus berlayar sejauh 10 km dengan sudut 30 derajat terhadap garis pantai. Setelah mencapai titik tengah perjalanan, kapal tersebut berbelok dan berlayar menuju pelabuhan C yang merupakan cerminan dari pelabuhan B terhadap garis pantai. Berapa jarak yang harus ditempuh kapal dari titik tengah perjalanan hingga mencapai pelabuhan C?

Menghitung Koordinat Bayangan Titik

Menghitung koordinat bayangan titik setelah direfleksikan merupakan aplikasi penting dari konsep refleksi. Soal ini menguji pemahaman kamu tentang bagaimana refleksi memengaruhi koordinat suatu titik.

• Titik A(2, 3) direfleksikan terhadap sumbu-x. Tentukan koordinat bayangan titik A.

Sifat-Sifat Refleksi

Soal ini menguji pemahaman kamu tentang sifat-sifat refleksi, seperti jarak titik ke garis refleksi, sudut antara garis refleksi dan garis yang menghubungkan titik dan bayangannya, dan sifat-sifat khusus lainnya.

• Jelaskan sifat-sifat refleksi yang berlaku pada titik A dan bayangannya A’ setelah direfleksikan terhadap garis y = x.

Penyelesaian Soal Refleksi

Refleksi merupakan salah satu transformasi geometri yang penting dalam matematika. Refleksi adalah pencerminan suatu objek terhadap garis atau titik tertentu. Dalam mempelajari refleksi, pemahaman tentang langkah-langkah penyelesaian soal menjadi kunci untuk memahami konsepnya dan menyelesaikan masalah-masalah yang terkait dengan refleksi.

Langkah-langkah Penyelesaian Soal Refleksi

Berikut adalah langkah-langkah umum dalam menyelesaikan soal refleksi:

• Identifikasi Titik atau Garis Refleksi: Langkah pertama adalah menentukan titik atau garis yang akan digunakan sebagai cermin untuk merefleksikan objek.
• Tentukan Jarak Titik ke Titik Refleksi: Hitung jarak tegak lurus dari setiap titik pada objek ke titik atau garis refleksi. Jarak ini akan sama dengan jarak antara titik asli dan titik refleksinya.
• Tentukan Titik Refleksi: Untuk setiap titik pada objek, tentukan titik refleksinya dengan menggunakan jarak yang telah dihitung. Titik refleksi berada di sisi lain dari titik refleksi dengan jarak yang sama.
• Hubungkan Titik Refleksi: Hubungkan titik-titik refleksi untuk membentuk objek yang direfleksikan. Objek yang direfleksikan akan memiliki bentuk dan ukuran yang sama dengan objek asli, tetapi berada di sisi lain dari titik atau garis refleksi.

Contoh Soal Refleksi dan Penyelesaiannya

Berikut adalah contoh soal refleksi dan langkah-langkah penyelesaiannya:

Soal: Refleksikan titik A(2,3) terhadap sumbu-y.

Penyelesaian:

1. Identifikasi Titik Refleksi: Titik refleksi adalah sumbu-y.
2. Tentukan Jarak Titik ke Titik Refleksi: Jarak titik A(2,3) ke sumbu-y adalah 2 satuan.
3. Tentukan Titik Refleksi: Titik refleksi A’ berada di sisi lain sumbu-y dengan jarak 2 satuan. Karena titik A berada di sebelah kanan sumbu-y, maka A’ akan berada di sebelah kiri sumbu-y dengan koordinat (-2,3).
4. Hubungkan Titik Refleksi: Titik A'(-2,3) adalah titik refleksi dari titik A(2,3) terhadap sumbu-y.

Ilustrasi Gambar:

Gambar di bawah menunjukkan titik A(2,3) dan titik refleksinya A'(-2,3) terhadap sumbu-y. Titik A dan A’ berada pada jarak yang sama dari sumbu-y.

[Gambar ilustrasi yang menunjukkan titik A(2,3) dan titik refleksinya A'(-2,3) terhadap sumbu-y, dengan sumbu-y sebagai garis refleksi. Titik A dan A’ berada pada jarak yang sama dari sumbu-y.]

Hubungan Refleksi dengan Transformasi Lainnya: Contoh Soal Refleksi Matematika Kelas 11

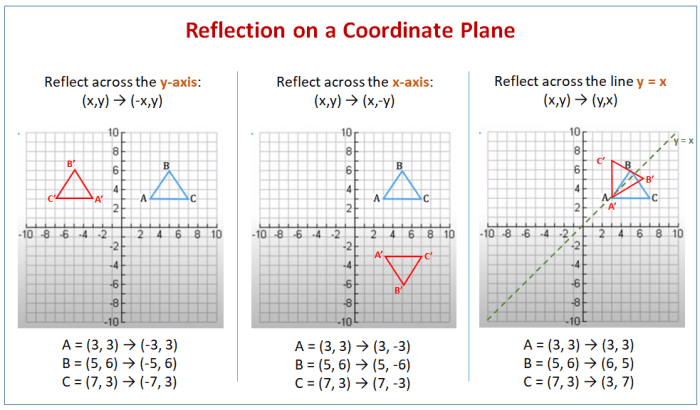
Refleksi merupakan salah satu transformasi geometri yang penting dalam matematika. Refleksi adalah transformasi yang menghasilkan bayangan cermin dari suatu objek. Bayangan cermin ini terbentuk dengan cara memantulkan setiap titik pada objek terhadap sebuah garis yang disebut garis refleksi. Selain refleksi, kita juga mengenal transformasi geometri lainnya seperti rotasi dan translasi. Ketiga transformasi ini memiliki hubungan erat satu sama lain, dan seringkali digabungkan untuk menghasilkan transformasi yang lebih kompleks.

Hubungan Refleksi dengan Rotasi dan Translasi

Refleksi, rotasi, dan translasi memiliki hubungan yang erat satu sama lain. Kita dapat melihat bahwa refleksi dapat dibentuk dengan menggabungkan rotasi dan translasi. Sebagai contoh, jika kita melakukan refleksi terhadap sumbu-x, kita dapat memperoleh hasil yang sama dengan melakukan rotasi sebesar 180 derajat terhadap titik asal, kemudian dilanjutkan dengan translasi sepanjang sumbu-y.

Contoh Soal yang Menggabungkan Refleksi dengan Transformasi Lainnya

Berikut ini adalah contoh soal yang menggabungkan refleksi dengan transformasi lainnya:

• Sebuah segitiga ABC direfleksikan terhadap garis y = x, kemudian dirotasikan sebesar 90 derajat berlawanan arah jarum jam terhadap titik asal. Tentukan koordinat bayangan segitiga ABC setelah dilakukan kedua transformasi tersebut.

Untuk menyelesaikan soal ini, kita dapat melakukan transformasi secara bertahap. Pertama, kita refleksikan segitiga ABC terhadap garis y = x. Kemudian, kita rotasikan bayangan segitiga ABC sebesar 90 derajat berlawanan arah jarum jam terhadap titik asal. Dengan demikian, kita akan memperoleh koordinat bayangan segitiga ABC setelah dilakukan kedua transformasi tersebut.

Penggunaan Refleksi dalam Menyelesaikan Masalah Transformasi Geometri

Refleksi dapat digunakan untuk menyelesaikan berbagai masalah transformasi geometri. Beberapa contohnya adalah:

• Menentukan simetri suatu objek.
• Mencari bayangan suatu objek setelah dilakukan transformasi.
• Membuat pola-pola geometris yang kompleks.

Sebagai contoh, untuk menentukan simetri suatu objek, kita dapat melakukan refleksi terhadap garis yang membagi objek tersebut menjadi dua bagian yang sama. Jika bayangan objek tersebut sama dengan objek aslinya, maka objek tersebut memiliki simetri terhadap garis refleksi tersebut.

Pentingnya Memahami Refleksi

Refleksi dalam matematika adalah transformasi geometri yang menghasilkan bayangan cermin dari suatu objek. Bayangan cermin ini dihasilkan dengan memindahkan objek ke sisi lain dari garis atau titik yang disebut garis refleksi atau titik refleksi. Konsep refleksi sangat penting dalam matematika karena memiliki aplikasi yang luas dalam berbagai bidang, mulai dari geometri hingga fisika.

Aplikasi Refleksi dalam Berbagai Bidang

Memahami konsep refleksi sangat penting dalam berbagai bidang, baik dalam matematika itu sendiri maupun dalam kehidupan sehari-hari. Refleksi memiliki peran penting dalam memecahkan masalah di bidang-bidang seperti:

• Geometri: Refleksi digunakan untuk memahami dan mempelajari sifat-sifat bangun geometri, seperti simetri, kongruensi, dan transformasi geometri lainnya.
• Fisika: Refleksi cahaya dan suara adalah fenomena penting dalam fisika. Memahami refleksi membantu kita memahami bagaimana cahaya dan suara dipantulkan dari permukaan, dan bagaimana mereka membentuk bayangan.
• Seni: Refleksi digunakan dalam seni untuk menciptakan efek visual yang menarik, seperti refleksi objek dalam air atau cermin.
• Arsitektur: Refleksi digunakan dalam desain bangunan untuk menciptakan efek visual yang menarik, seperti pencahayaan dan ilusi optik.

Contoh Kasus Nyata Aplikasi Refleksi

Salah satu contoh kasus nyata aplikasi refleksi dalam kehidupan sehari-hari adalah penggunaan cermin. Cermin merupakan alat yang memanfaatkan prinsip refleksi untuk menghasilkan bayangan. Ketika kita berdiri di depan cermin, cahaya dari tubuh kita dipantulkan oleh permukaan cermin, menciptakan bayangan yang kita lihat. Refleksi juga digunakan dalam berbagai alat optik, seperti teleskop, mikroskop, dan kamera, untuk memfokuskan cahaya dan menghasilkan gambar yang lebih jelas.

Contoh soal refleksi matematika kelas 11 bisa mencakup berbagai macam konsep, mulai dari pencerminan terhadap sumbu x dan y, hingga refleksi terhadap garis. Nah, kalau kamu lagi belajar tentang gerak lurus beraturan (GLB), kamu bisa coba latihan soal contoh soal glbb kelas 10 untuk memahami konsep kecepatan dan jarak tempuh.

Setelah itu, kamu bisa kembali ke soal refleksi matematika kelas 11 dan mencoba menghubungkan konsep-konsep tersebut untuk memecahkan masalah yang lebih kompleks.

Latihan Soal Refleksi

Refleksi dalam matematika adalah transformasi geometri yang menghasilkan bayangan suatu objek terhadap suatu garis atau titik. Refleksi dapat diartikan sebagai pencerminan suatu objek terhadap suatu garis atau titik.

Soal Refleksi Berbagai Tingkat Kesulitan

Berikut ini adalah contoh soal refleksi dengan berbagai tingkat kesulitan yang dapat digunakan untuk menguji pemahaman konsep dan kemampuan aplikasi:

• Soal Mudah:
• Tentukan bayangan titik A(2,3) jika direfleksikan terhadap sumbu x.
• Gambarlah bayangan segitiga ABC dengan titik A(1,2), B(3,1), dan C(2,4) jika direfleksikan terhadap sumbu y.
• Soal Sedang:
• Tentukan bayangan garis y = 2x + 1 jika direfleksikan terhadap garis y = x.
• Tentukan bayangan persegi panjang ABCD dengan titik A(1,1), B(3,1), C(3,3), dan D(1,3) jika direfleksikan terhadap titik O(0,0).
• Soal Sulit:
• Tentukan bayangan lingkaran x² + y² = 4 jika direfleksikan terhadap garis y = -x.
• Tentukan bayangan parabola y = x² jika direfleksikan terhadap titik (2,1).

Kunci Jawaban Soal Refleksi

Berikut adalah kunci jawaban untuk setiap soal refleksi yang telah dibuat:

• Soal Mudah:
• Bayangan titik A(2,3) jika direfleksikan terhadap sumbu x adalah A'(2,-3).
• Bayangan segitiga ABC dengan titik A(1,2), B(3,1), dan C(2,4) jika direfleksikan terhadap sumbu y adalah A'(-1,2), B'(-3,1), dan C'(-2,4).
• Soal Sedang:
• Bayangan garis y = 2x + 1 jika direfleksikan terhadap garis y = x adalah x = 2y + 1.
• Bayangan persegi panjang ABCD dengan titik A(1,1), B(3,1), C(3,3), dan D(1,3) jika direfleksikan terhadap titik O(0,0) adalah A'(-1,-1), B'(-3,-1), C'(-3,-3), dan D'(-1,-3).
• Soal Sulit:
• Bayangan lingkaran x² + y² = 4 jika direfleksikan terhadap garis y = -x adalah y² + x² = 4.
• Bayangan parabola y = x² jika direfleksikan terhadap titik (2,1) adalah y = (x – 4)² + 1.

Soal Refleksi yang Menguji Pemahaman Konsep dan Kemampuan Aplikasi

Berikut adalah contoh soal refleksi yang dirancang untuk menguji pemahaman konsep dan kemampuan aplikasi:

• Jelaskan bagaimana menentukan bayangan suatu titik jika direfleksikan terhadap suatu garis.
• Tentukan bayangan suatu bangun datar jika direfleksikan terhadap suatu garis dan kemudian direfleksikan terhadap garis lain.
• Tentukan bayangan suatu bangun datar jika direfleksikan terhadap suatu titik dan kemudian direfleksikan terhadap titik lain.
• Terapkan konsep refleksi untuk menyelesaikan masalah geometri, seperti mencari simetri suatu bangun datar atau mencari jarak terpendek antara dua titik.

Contoh Soal Refleksi

Berikut ini adalah contoh soal refleksi yang dapat digunakan untuk menguji pemahaman konsep dan kemampuan aplikasi:

• Tentukan bayangan titik A(2,3) jika direfleksikan terhadap garis y = x.
• Tentukan bayangan segitiga ABC dengan titik A(1,2), B(3,1), dan C(2,4) jika direfleksikan terhadap titik O(0,0).
• Tentukan bayangan parabola y = x² jika direfleksikan terhadap garis y = -x.
• Sebuah persegi panjang ABCD dengan titik A(1,1), B(3,1), C(3,3), dan D(1,3) direfleksikan terhadap garis y = x. Tentukan koordinat bayangan persegi panjang ABCD.
• Tentukan bayangan lingkaran x² + y² = 9 jika direfleksikan terhadap titik (2,1).

Pembahasan Soal Refleksi

Berikut ini adalah pembahasan untuk setiap soal refleksi yang telah dibuat:

• Soal 1:
• Untuk menentukan bayangan titik A(2,3) jika direfleksikan terhadap garis y = x, kita dapat menggunakan rumus refleksi terhadap garis y = x:
  

  (x’, y’) = (y, x)

  Dengan demikian, bayangan titik A(2,3) adalah A'(3,2).

• Soal 2:
• Untuk menentukan bayangan segitiga ABC dengan titik A(1,2), B(3,1), dan C(2,4) jika direfleksikan terhadap titik O(0,0), kita dapat menggunakan rumus refleksi terhadap titik O(0,0):
  

  (x’, y’) = (-x, -y)

  Dengan demikian, bayangan titik A(1,2) adalah A'(-1,-2), bayangan titik B(3,1) adalah B'(-3,-1), dan bayangan titik C(2,4) adalah C'(-2,-4). Bayangan segitiga ABC adalah segitiga A’B’C’ dengan titik A'(-1,-2), B'(-3,-1), dan C'(-2,-4).

• Soal 3:
• Untuk menentukan bayangan parabola y = x² jika direfleksikan terhadap garis y = -x, kita dapat menggunakan rumus refleksi terhadap garis y = -x:
  

  (x’, y’) = (-y, -x)

  Dengan demikian, bayangan parabola y = x² adalah x = y².

• Soal 4:
• Untuk menentukan bayangan persegi panjang ABCD dengan titik A(1,1), B(3,1), C(3,3), dan D(1,3) jika direfleksikan terhadap garis y = x, kita dapat menggunakan rumus refleksi terhadap garis y = x:
  

  (x’, y’) = (y, x)

  Dengan demikian, bayangan titik A(1,1) adalah A'(1,1), bayangan titik B(3,1) adalah B'(1,3), bayangan titik C(3,3) adalah C'(3,3), dan bayangan titik D(1,3) adalah D'(3,1). Bayangan persegi panjang ABCD adalah persegi panjang A’B’C’D’ dengan titik A'(1,1), B'(1,3), C'(3,3), dan D'(3,1).

• Soal 5:
• Untuk menentukan bayangan lingkaran x² + y² = 9 jika direfleksikan terhadap titik (2,1), kita dapat menggunakan rumus refleksi terhadap titik (2,1):
  

  (x’, y’) = (2(2) – x, 2(1) – y)

  Dengan demikian, bayangan lingkaran x² + y² = 9 adalah (x – 4)² + (y – 2)² = 9.

Akhir Kata

Dengan memahami konsep refleksi, kamu tidak hanya akan lebih mahir dalam menyelesaikan soal-soal matematika, tetapi juga dapat mengaplikasikannya dalam berbagai bidang, seperti seni, desain, arsitektur, fotografi, dan bahkan dalam kehidupan sehari-hari. Selamat mencoba!