Contoh Soal Relasi dan Fungsi: Memahami Hubungan Antar Himpunan

Contoh soal relasi dan fungsi – Pernahkah kamu bertanya-tanya bagaimana cara menggambarkan hubungan antar kelompok benda atau data? Nah, di dunia matematika, relasi dan fungsi hadir sebagai alat yang ampuh untuk menjawab pertanyaan ini. Relasi dan fungsi berperan penting dalam menggambarkan hubungan antar himpunan, seperti hubungan antara siswa dengan nilai ujiannya atau hubungan antara waktu dengan jarak tempuh suatu kendaraan.

Contoh Soal Relasi dan Fungsi mengajak kita untuk memahami konsep relasi dan fungsi secara lebih mendalam. Melalui contoh-contoh soal yang menarik dan beragam, kita akan belajar bagaimana menentukan relasi dan fungsi, mengenal jenis-jenisnya, dan mengaplikasikannya dalam berbagai situasi.

Pengertian Relasi dan Fungsi

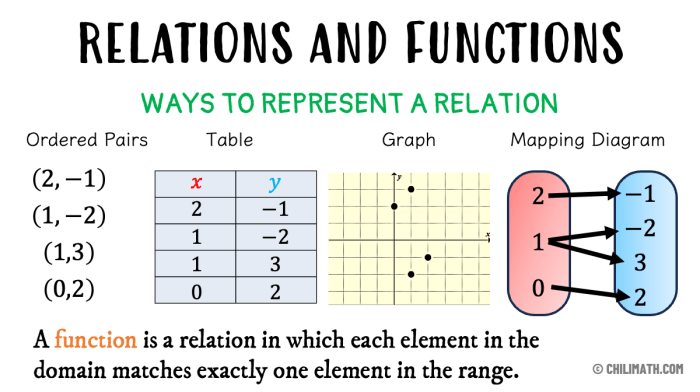
Relasi dan fungsi merupakan konsep dasar dalam matematika yang sering kita jumpai dalam kehidupan sehari-hari. Meskipun keduanya mungkin terdengar mirip, keduanya memiliki perbedaan mendasar. Relasi adalah hubungan antara dua himpunan, sedangkan fungsi adalah jenis relasi khusus yang menghubungkan setiap elemen pada himpunan pertama dengan tepat satu elemen pada himpunan kedua.

Pengertian Relasi

Relasi dalam matematika didefinisikan sebagai hubungan antara dua himpunan atau lebih. Relasi dapat diartikan sebagai suatu aturan atau pola yang menghubungkan elemen-elemen dari himpunan yang satu dengan elemen-elemen dari himpunan yang lain.

Contoh sederhana relasi adalah hubungan antara siswa dengan mata pelajaran yang mereka pelajari. Misalnya, di kelas 10 terdapat 30 siswa dan 5 mata pelajaran. Setiap siswa dapat mengambil lebih dari satu mata pelajaran, dan setiap mata pelajaran dapat dipelajari oleh lebih dari satu siswa. Hubungan ini dapat direpresentasikan sebagai relasi.

Pengertian Fungsi

Fungsi merupakan jenis relasi khusus yang menghubungkan setiap elemen pada himpunan pertama dengan tepat satu elemen pada himpunan kedua. Artinya, setiap elemen pada himpunan pertama (disebut domain) hanya memiliki satu pasangan yang unik pada himpunan kedua (disebut kodomain).

Contoh sederhana fungsi adalah mesin penjual otomatis. Setiap tombol pada mesin mewakili input (domain), dan setiap tombol hanya mengeluarkan satu jenis minuman (kodomain).

Contoh Relasi dan Fungsi dalam Kehidupan Sehari-hari

Berikut beberapa contoh relasi dan fungsi dalam kehidupan sehari-hari:

• Relasi: Hubungan antara siswa dengan kelas yang mereka ikuti.
• Relasi: Hubungan antara kota dengan kode posnya.
• Relasi: Hubungan antara nama orang dengan tanggal lahirnya.
• Fungsi: Mesin penjual otomatis, di mana setiap tombol hanya mengeluarkan satu jenis minuman.
• Fungsi: Termometer, yang menghubungkan suhu dengan angka pada skala termometer.
• Fungsi: Alat ukur kecepatan, yang menghubungkan jarak yang ditempuh dengan waktu tempuh.

Perbedaan Relasi dan Fungsi

Berikut tabel yang membandingkan relasi dan fungsi berdasarkan ciri-ciri dan contohnya:

Ciri	Relasi	Fungsi
Definisi	Hubungan antara dua himpunan atau lebih	Jenis relasi khusus yang menghubungkan setiap elemen pada himpunan pertama dengan tepat satu elemen pada himpunan kedua
Contoh	Hubungan antara siswa dengan mata pelajaran yang mereka pelajari	Mesin penjual otomatis, di mana setiap tombol hanya mengeluarkan satu jenis minuman
Pasangan	Elemen pada himpunan pertama dapat memiliki lebih dari satu pasangan pada himpunan kedua	Setiap elemen pada himpunan pertama hanya memiliki satu pasangan yang unik pada himpunan kedua
Diagram Panah	Panah dapat keluar dari satu titik pada himpunan pertama menuju lebih dari satu titik pada himpunan kedua	Panah hanya keluar dari satu titik pada himpunan pertama menuju satu titik pada himpunan kedua

Jenis-jenis Relasi dan Fungsi

Relasi dan fungsi merupakan konsep dasar dalam matematika yang memiliki peran penting dalam berbagai bidang, seperti ilmu komputer, ekonomi, dan fisika. Relasi dan fungsi dapat dibedakan berdasarkan sifatnya, yaitu bagaimana elemen-elemen dalam himpunan domain dan kodomain saling berhubungan.

Jenis-jenis Relasi Berdasarkan Sifatnya

Relasi dapat diklasifikasikan berdasarkan sifatnya, yaitu bagaimana elemen-elemen dalam himpunan domain dan kodomain saling berhubungan. Ada empat jenis relasi berdasarkan sifatnya:

• Relasi Satu-satu: Dalam relasi satu-satu, setiap elemen dalam himpunan domain dipasangkan dengan tepat satu elemen dalam himpunan kodomain, dan sebaliknya. Contoh: Relasi “adalah ibu dari” antara himpunan perempuan dan himpunan anak-anak. Setiap perempuan hanya memiliki satu ibu, dan setiap anak hanya memiliki satu ibu.
• Relasi Banyak-satu: Dalam relasi banyak-satu, beberapa elemen dalam himpunan domain dipasangkan dengan satu elemen dalam himpunan kodomain. Contoh: Relasi “berada di kota” antara himpunan orang dan himpunan kota. Beberapa orang bisa berada di kota yang sama, tetapi setiap orang hanya berada di satu kota.
• Relasi Satu-banyak: Dalam relasi satu-banyak, satu elemen dalam himpunan domain dipasangkan dengan beberapa elemen dalam himpunan kodomain. Contoh: Relasi “memiliki anak” antara himpunan orang tua dan himpunan anak. Seorang orang tua bisa memiliki beberapa anak, tetapi setiap anak hanya memiliki satu orang tua.
• Relasi Banyak-banyak: Dalam relasi banyak-banyak, beberapa elemen dalam himpunan domain dipasangkan dengan beberapa elemen dalam himpunan kodomain. Contoh: Relasi “berteman dengan” antara himpunan orang. Beberapa orang bisa berteman dengan beberapa orang lain, dan sebaliknya.

Jenis-jenis Fungsi Berdasarkan Sifatnya

Fungsi merupakan jenis khusus dari relasi yang memiliki sifat khusus, yaitu setiap elemen dalam himpunan domain dipasangkan dengan tepat satu elemen dalam himpunan kodomain. Fungsi dapat diklasifikasikan berdasarkan sifatnya, yaitu bagaimana fungsi tersebut berubah terhadap inputnya. Ada beberapa jenis fungsi berdasarkan sifatnya, antara lain:

• Fungsi Linear: Fungsi linear adalah fungsi yang grafiknya berupa garis lurus. Fungsi linear dapat ditulis dalam bentuk y = mx + c, di mana m adalah gradien garis dan c adalah konstanta. Contoh: Fungsi y = 2x + 1 adalah fungsi linear dengan gradien 2 dan konstanta 1.
• Fungsi Kuadrat: Fungsi kuadrat adalah fungsi yang grafiknya berupa parabola. Fungsi kuadrat dapat ditulis dalam bentuk y = ax² + bx + c, di mana a, b, dan c adalah konstanta. Contoh: Fungsi y = x² + 2x + 1 adalah fungsi kuadrat dengan a = 1, b = 2, dan c = 1.
• Fungsi Eksponensial: Fungsi eksponensial adalah fungsi yang grafiknya berupa kurva yang naik dengan cepat. Fungsi eksponensial dapat ditulis dalam bentuk y = a^x, di mana a adalah konstanta positif dan x adalah variabel. Contoh: Fungsi y = 2^x adalah fungsi eksponensial dengan a = 2.
• Fungsi Logaritma: Fungsi logaritma adalah fungsi yang merupakan kebalikan dari fungsi eksponensial. Fungsi logaritma dapat ditulis dalam bentuk y = log_ax, di mana a adalah konstanta positif dan x adalah variabel. Contoh: Fungsi y = log₂x adalah fungsi logaritma dengan a = 2.

Tabel Jenis-jenis Relasi dan Fungsi

Berikut tabel yang merangkum jenis-jenis relasi dan fungsi beserta contohnya:

Jenis	Definisi	Contoh
Relasi Satu-satu	Setiap elemen dalam himpunan domain dipasangkan dengan tepat satu elemen dalam himpunan kodomain, dan sebaliknya.	Relasi “adalah ibu dari” antara himpunan perempuan dan himpunan anak-anak.
Relasi Banyak-satu	Beberapa elemen dalam himpunan domain dipasangkan dengan satu elemen dalam himpunan kodomain.	Relasi “berada di kota” antara himpunan orang dan himpunan kota.
Relasi Satu-banyak	Satu elemen dalam himpunan domain dipasangkan dengan beberapa elemen dalam himpunan kodomain.	Relasi “memiliki anak” antara himpunan orang tua dan himpunan anak.
Relasi Banyak-banyak	Beberapa elemen dalam himpunan domain dipasangkan dengan beberapa elemen dalam himpunan kodomain.	Relasi “berteman dengan” antara himpunan orang.
Fungsi Linear	Fungsi yang grafiknya berupa garis lurus.	y = 2x + 1
Fungsi Kuadrat	Fungsi yang grafiknya berupa parabola.	y = x2 + 2x + 1
Fungsi Eksponensial	Fungsi yang grafiknya berupa kurva yang naik dengan cepat.	y = 2x
Fungsi Logaritma	Fungsi yang merupakan kebalikan dari fungsi eksponensial.	y = log2x

Cara Menentukan Relasi dan Fungsi: Contoh Soal Relasi Dan Fungsi

Relasi dan fungsi merupakan konsep dasar dalam matematika yang menjelaskan hubungan antara dua himpunan. Relasi menunjukkan hubungan yang mungkin ada antara elemen-elemen dari dua himpunan, sementara fungsi merupakan jenis khusus dari relasi yang memetakan setiap elemen dari himpunan pertama ke tepat satu elemen dari himpunan kedua. Untuk memahami relasi dan fungsi dengan lebih baik, kita perlu mengetahui cara menentukannya dari suatu himpunan pasangan berurutan.

Menentukan Relasi dan Fungsi dari Himpunan Pasangan Berurutan

Relasi dan fungsi dapat ditentukan dari himpunan pasangan berurutan dengan memperhatikan hubungan antara elemen-elemennya. Berikut adalah langkah-langkah yang dapat digunakan:

• Identifikasi domain dan kodomain: Domain adalah himpunan pertama yang elemennya merupakan anggota pertama dari setiap pasangan berurutan. Kodomain adalah himpunan kedua yang elemennya merupakan anggota kedua dari setiap pasangan berurutan.
• Perhatikan hubungan antar elemen: Hubungan antar elemen dalam pasangan berurutan menunjukkan relasi antara domain dan kodomain.
• Tentukan apakah relasi tersebut merupakan fungsi: Relasi merupakan fungsi jika setiap elemen di domain dipetakan ke tepat satu elemen di kodomain.

Contoh Soal Menentukan Relasi dan Fungsi

Misalkan kita memiliki himpunan pasangan berurutan berikut: (1, 2), (2, 4), (3, 6), (4, 8).

1. Identifikasi domain dan kodomain:
   • Domain = 1, 2, 3, 4
   • Kodomain = 2, 4, 6, 8
2. Perhatikan hubungan antar elemen: Setiap elemen di domain dikalikan dengan 2 untuk menghasilkan elemen di kodomain.
3. Tentukan apakah relasi tersebut merupakan fungsi: Ya, relasi tersebut merupakan fungsi karena setiap elemen di domain dipetakan ke tepat satu elemen di kodomain.

Diagram Panah untuk Menunjukkan Relasi dan Fungsi

Diagram panah dapat digunakan untuk memvisualisasikan relasi dan fungsi. Pada diagram panah, domain dan kodomain digambarkan sebagai dua himpunan terpisah, dan panah menghubungkan elemen-elemen yang berpasangan.

Sebagai contoh, diagram panah untuk himpunan pasangan berurutan (1, 2), (2, 4), (3, 6), (4, 8) akan terlihat seperti ini:

[Diagram panah yang menunjukkan domain 1, 2, 3, 4 dan kodomain 2, 4, 6, 8 dengan panah menghubungkan setiap elemen domain ke elemen kodomain yang sesuai. Misalnya, panah menghubungkan 1 ke 2, 2 ke 4, 3 ke 6, dan 4 ke 8.]

Diagram panah menunjukkan bahwa relasi tersebut merupakan fungsi karena setiap elemen di domain hanya memiliki satu panah keluar yang menghubungkannya ke elemen di kodomain.

Notasi Fungsi

Notasi fungsi adalah cara penulisan yang digunakan untuk menyatakan hubungan antara input dan output dalam suatu fungsi. Penulisan notasi fungsi sangat penting dalam matematika karena memungkinkan kita untuk menyatakan hubungan tersebut secara ringkas dan mudah dipahami.

Cara Penulisan Notasi Fungsi

Notasi fungsi biasanya ditulis dengan menggunakan huruf kecil seperti f, g, atau h, diikuti oleh tanda kurung yang berisi variabel input. Contohnya, f(x) menyatakan fungsi f dengan variabel input x.

• f(x) = y, di mana f adalah nama fungsi, x adalah variabel input, dan y adalah variabel output.
• Misalnya, fungsi f(x) = 2x + 1 berarti bahwa untuk setiap nilai x yang dimasukkan, outputnya adalah 2x + 1.

Menentukan Nilai Fungsi

Untuk menentukan nilai fungsi untuk suatu nilai input tertentu, kita cukup mengganti variabel input dalam rumus fungsi dengan nilai input tersebut.

Contoh Soal

Misalnya, jika kita ingin menentukan nilai fungsi f(x) = 2x + 1 untuk x = 3, maka kita cukup mengganti x dengan 3 dalam rumus fungsi.

f(3) = 2(3) + 1 = 6 + 1 = 7

Jadi, nilai fungsi f(x) = 2x + 1 untuk x = 3 adalah 7.

Menentukan Rumus Fungsi dari Grafik

Rumus fungsi dapat ditentukan dari grafiknya dengan melihat pola hubungan antara input dan output.

Contoh Soal

Misalnya, jika kita memiliki grafik fungsi yang melewati titik (1, 2) dan (2, 4), maka kita dapat menentukan rumus fungsi sebagai berikut:

1. Tentukan selisih antara nilai output untuk setiap titik. Dalam contoh ini, selisihnya adalah 4 – 2 = 2.
2. Tentukan selisih antara nilai input untuk setiap titik. Dalam contoh ini, selisihnya adalah 2 – 1 = 1.
3. Bagi selisih output dengan selisih input. Dalam contoh ini, hasilnya adalah 2/1 = 2.
4. Hasil pembagian tersebut merupakan kemiringan garis. Dalam contoh ini, kemiringan garis adalah 2.
5. Tentukan titik potong garis dengan sumbu y. Dalam contoh ini, titik potong garis dengan sumbu y adalah (0, 0).
6. Rumus fungsi dapat ditulis sebagai y = mx + c, di mana m adalah kemiringan garis dan c adalah titik potong garis dengan sumbu y.
7. Dalam contoh ini, rumus fungsi adalah y = 2x + 0, atau y = 2x.

Jadi, rumus fungsi untuk grafik yang melewati titik (1, 2) dan (2, 4) adalah y = 2x.

Fungsi Komposisi

Fungsi komposisi merupakan operasi matematika yang menggabungkan dua fungsi untuk membentuk fungsi baru. Fungsi komposisi dihasilkan dengan menerapkan fungsi pertama ke output fungsi kedua. Dengan kata lain, fungsi komposisi adalah fungsi yang bekerja pada fungsi lain, menghasilkan output baru.

Contoh soal relasi dan fungsi seringkali melibatkan pemahaman tentang konsep-konsep dasar, seperti menentukan domain dan range. Namun, pemahaman ini juga bisa diterapkan dalam soal-soal yang lebih kompleks, seperti menghitung volume tabung. Nah, untuk mengasah kemampuanmu dalam menghitung volume tabung, kamu bisa berlatih dengan contoh soal tabung kelas 9 yang bisa kamu temukan di situs ini.

Dengan berlatih, kamu akan semakin mahir dalam memahami konsep relasi dan fungsi, serta aplikasinya dalam soal-soal yang lebih menantang.

Definisi dan Cara Menghitung Fungsi Komposisi

Fungsi komposisi didefinisikan sebagai operasi yang menggabungkan dua fungsi, f dan g, menjadi fungsi baru, yang disebut komposisi f dengan g, dilambangkan dengan f o g. Fungsi komposisi f o g menghasilkan output yang sama dengan menerapkan fungsi g terlebih dahulu pada input, kemudian menerapkan fungsi f pada output g.

Cara menghitung fungsi komposisi adalah dengan mensubstitusikan output dari fungsi pertama (g(x)) sebagai input ke fungsi kedua (f(x)). Secara matematis, fungsi komposisi f o g dapat ditulis sebagai:

(f o g)(x) = f(g(x))

Contoh Soal Menentukan Fungsi Komposisi

Misalkan kita memiliki dua fungsi, f(x) = x^2 + 1 dan g(x) = 2x – 3. Untuk menentukan fungsi komposisi f o g, kita perlu mengganti g(x) ke dalam f(x):

(f o g)(x) = f(g(x)) = f(2x – 3) = (2x – 3)^2 + 1

Dengan demikian, fungsi komposisi f o g adalah (2x – 3)^2 + 1.

Sifat-sifat Fungsi Komposisi

Fungsi komposisi memiliki beberapa sifat penting, yaitu:

• Tidak komutatif: f o g ≠ g o f, umumnya fungsi komposisi tidak komutatif. Artinya, urutan fungsi yang dikomposisikan mempengaruhi hasilnya.
• Asosiatif: (f o g) o h = f o (g o h), fungsi komposisi bersifat asosiatif. Artinya, urutan pengelompokan fungsi tidak mempengaruhi hasilnya.
• Identitas: f o I = I o f = f, fungsi identitas (I(x) = x) tidak mengubah fungsi saat dikomposisikan.

Contoh Penerapan Fungsi Komposisi

Fungsi komposisi banyak digunakan dalam berbagai bidang, seperti:

• Fisika: Fungsi komposisi digunakan untuk memodelkan gerakan benda yang dipengaruhi oleh beberapa gaya.
• Ekonomi: Fungsi komposisi digunakan untuk menganalisis pengaruh perubahan harga terhadap permintaan dan penawaran.
• Komputer: Fungsi komposisi digunakan dalam pemrograman untuk membangun fungsi yang kompleks dari fungsi yang lebih sederhana.

Fungsi Invers

Fungsi invers merupakan konsep penting dalam matematika yang berkaitan dengan hubungan timbal balik antara dua fungsi. Sederhananya, fungsi invers adalah fungsi yang “membalikkan” efek dari fungsi asalnya.

Pengertian Fungsi Invers

Fungsi invers dari suatu fungsi f(x) adalah fungsi yang dinotasikan sebagai f⁻¹(x) yang memenuhi sifat berikut:

Jika f(a) = b, maka f⁻¹(b) = a.

Dengan kata lain, jika fungsi f memetakan nilai a ke b, maka fungsi inversnya, f⁻¹, memetakan nilai b kembali ke a.

Cara Menentukan Fungsi Invers

Untuk menentukan fungsi invers dari suatu fungsi, kita dapat mengikuti langkah-langkah berikut:

1. Ganti f(x) dengan y.
2. Tukar variabel x dan y.
3. Selesaikan persamaan untuk y.
4. Ganti y dengan f⁻¹(x).

Contoh Soal Menentukan Fungsi Invers

Misalkan kita ingin menentukan fungsi invers dari fungsi f(x) = 2x + 1.

1. Ganti f(x) dengan y: y = 2x + 1.
2. Tukar x dan y: x = 2y + 1.
3. Selesaikan persamaan untuk y:
   1. Kurangi 1 dari kedua ruas: x – 1 = 2y.
   2. Bagi kedua ruas dengan 2: (x – 1)/2 = y.
4. Ganti y dengan f⁻¹(x): f⁻¹(x) = (x – 1)/2.

Jadi, fungsi invers dari f(x) = 2x + 1 adalah f⁻¹(x) = (x – 1)/2.

Hubungan Fungsi dan Inversnya

Fungsi dan inversnya memiliki hubungan yang erat. Berikut adalah beberapa poin penting:

• Grafik fungsi dan inversnya simetris terhadap garis y = x.
• Komposisi fungsi f dan inversnya, f⁻¹, menghasilkan fungsi identitas, yaitu f(f⁻¹(x)) = x dan f⁻¹(f(x)) = x.
• Tidak semua fungsi memiliki invers. Fungsi yang memiliki invers disebut fungsi bijektif, yaitu fungsi yang sekaligus surjektif dan injektif.

Aplikasi Relasi dan Fungsi

Relasi dan fungsi merupakan konsep matematika yang memiliki aplikasi luas dalam berbagai bidang. Konsep ini membantu kita memahami dan menganalisis hubungan antara berbagai variabel dalam kehidupan nyata. Mari kita telusuri bagaimana relasi dan fungsi berperan dalam berbagai bidang.

Aplikasi Relasi dan Fungsi dalam Ekonomi

Relasi dan fungsi memegang peranan penting dalam analisis ekonomi. Misalnya, fungsi permintaan menunjukkan hubungan antara harga suatu barang dengan jumlah barang yang diminta oleh konsumen. Fungsi penawaran menunjukkan hubungan antara harga suatu barang dengan jumlah barang yang ditawarkan oleh produsen. Dengan menggunakan fungsi, ekonom dapat memprediksi perilaku pasar, menganalisis dampak perubahan harga terhadap permintaan dan penawaran, serta menentukan titik keseimbangan pasar.

Aplikasi Relasi dan Fungsi dalam Fisika

Dalam fisika, relasi dan fungsi digunakan untuk menggambarkan hubungan antara berbagai besaran fisika. Contohnya, fungsi kecepatan menunjukkan hubungan antara waktu dengan kecepatan suatu benda. Fungsi percepatan menunjukkan hubungan antara waktu dengan percepatan suatu benda. Dengan menggunakan fungsi, fisikawan dapat menganalisis gerak benda, menghitung jarak, kecepatan, dan percepatan, serta memahami berbagai fenomena fisika.

Aplikasi Relasi dan Fungsi dalam Informatika

Relasi dan fungsi juga memiliki peran penting dalam informatika. Dalam pemrograman, fungsi digunakan untuk mengelompokkan kode yang melakukan tugas tertentu. Relasi digunakan dalam database untuk mengatur hubungan antar tabel. Dengan menggunakan fungsi dan relasi, programmer dapat membangun aplikasi yang efisien, terstruktur, dan mudah dipelihara.

Contoh Soal Aplikasi Relasi dan Fungsi dalam Kehidupan Sehari-hari

• Misalnya, Anda ingin membeli buah di pasar. Harga buah biasanya ditentukan berdasarkan beratnya. Hubungan antara berat buah dan harga buah dapat dinyatakan sebagai fungsi linear. Jika harga 1 kg jeruk adalah Rp10.000, maka harga 2 kg jeruk adalah Rp20.000, dan seterusnya.
• Contoh lain, Anda ingin pergi ke suatu tempat menggunakan taksi. Tarif taksi biasanya ditentukan berdasarkan jarak tempuh. Hubungan antara jarak tempuh dan tarif taksi dapat dinyatakan sebagai fungsi linear. Jika tarif dasar taksi adalah Rp5.000 dan tarif per kilometer adalah Rp4.000, maka tarif taksi untuk jarak tempuh 5 km adalah Rp25.000.

Langkah-langkah Menyelesaikan Masalah dengan Relasi dan Fungsi, Contoh soal relasi dan fungsi

• Menganalisis masalah dan mengidentifikasi variabel yang terlibat.
• Menentukan hubungan antara variabel-variabel tersebut dalam bentuk relasi atau fungsi.
• Menuliskan persamaan atau rumus yang menggambarkan relasi atau fungsi tersebut.
• Memecahkan persamaan atau rumus untuk mendapatkan nilai yang diinginkan.
• Menerjemahkan hasil penyelesaian ke dalam konteks masalah.

Akhir Kata

Memahami relasi dan fungsi merupakan langkah penting dalam mempelajari matematika. Dengan memahami konsep ini, kita dapat menganalisis hubungan antar objek dan menyelesaikan masalah yang kompleks. Dari contoh-contoh soal yang telah kita pelajari, terlihat bahwa relasi dan fungsi memiliki aplikasi yang luas, mulai dari ilmu ekonomi hingga informatika.