Riset operasi, sebuah bidang ilmu yang menggabungkan matematika, statistika, dan ilmu komputer, berperan penting dalam membantu pengambilan keputusan optimal dalam berbagai situasi. ‘Contoh Soal Riset Operasi dan Jawabannya’ menjadi jembatan penting untuk memahami bagaimana konsep-konsep ini diterapkan dalam praktik.
Dari menentukan rute pengiriman barang yang paling efisien hingga mengalokasikan sumber daya secara optimal, riset operasi memiliki aplikasi luas di berbagai bidang, seperti bisnis, logistik, kesehatan, dan keuangan. Melalui contoh soal yang terstruktur dan disertai jawaban yang rinci, Anda dapat memperoleh pemahaman yang lebih mendalam tentang teknik dasar riset operasi, model-model yang digunakan, dan cara mengaplikasikannya dalam situasi nyata.
Pengenalan Riset Operasi
Riset operasi adalah disiplin ilmu yang menggunakan metode ilmiah dan matematika untuk membantu pengambilan keputusan yang optimal dalam menghadapi permasalahan kompleks. Riset operasi berfokus pada pemodelan sistem nyata, menganalisisnya dengan menggunakan teknik kuantitatif, dan kemudian memberikan solusi yang terbaik berdasarkan kriteria tertentu.
Konsep Dasar Riset Operasi
Riset operasi melibatkan beberapa konsep dasar, yaitu:
- Pemodelan: Riset operasi membangun model matematika untuk merepresentasikan sistem nyata, dengan mempertimbangkan variabel, batasan, dan tujuan yang ingin dicapai.
- Analisis: Setelah model dibuat, riset operasi menggunakan berbagai teknik matematika untuk menganalisis model dan mencari solusi yang optimal. Teknik yang umum digunakan meliputi pemrograman linear, pemrograman dinamis, teori antrian, dan teori permainan.
- Implementasi: Solusi yang diperoleh dari analisis model kemudian diimplementasikan dalam sistem nyata. Hal ini membutuhkan komunikasi yang efektif antara peneliti riset operasi dan pengambil keputusan.
Ruang Lingkup dan Aplikasi Riset Operasi
Riset operasi memiliki ruang lingkup yang luas dan dapat diaplikasikan dalam berbagai bidang, antara lain:
- Manajemen: Riset operasi dapat membantu dalam pengambilan keputusan strategis dan operasional, seperti perencanaan produksi, manajemen inventaris, penjadwalan, dan alokasi sumber daya.
- Keuangan: Riset operasi dapat digunakan untuk memaksimalkan keuntungan, meminimalkan risiko, dan mengoptimalkan portofolio investasi.
- Logistik: Riset operasi dapat digunakan untuk mengoptimalkan jaringan distribusi, perencanaan rute, dan manajemen rantai pasokan.
- Kesehatan: Riset operasi dapat membantu dalam pengalokasian sumber daya kesehatan, penjadwalan pasien, dan manajemen antrian.
- Militer: Riset operasi telah digunakan secara luas dalam militer untuk perencanaan operasi, strategi, dan logistik.
Contoh Kasus Riset Operasi dalam Kehidupan Nyata
Salah satu contoh kasus riset operasi adalah masalah penjadwalan penerbangan. Maskapai penerbangan menggunakan riset operasi untuk menentukan jadwal penerbangan yang optimal, dengan mempertimbangkan faktor-faktor seperti jumlah penumpang, waktu keberangkatan dan kedatangan, dan ketersediaan pesawat. Model riset operasi dapat membantu maskapai penerbangan memaksimalkan pendapatan dan meminimalkan biaya operasional.
Teknik Dasar Riset Operasi
Riset operasi adalah ilmu yang menggunakan metode ilmiah untuk membantu pengambilan keputusan yang optimal dalam menghadapi masalah kompleks. Metode ilmiah tersebut melibatkan proses pemodelan matematika, analisis, dan interpretasi untuk menemukan solusi terbaik bagi masalah yang dihadapi.
Pemodelan Matematika dalam Riset Operasi
Pemodelan matematika merupakan proses merepresentasikan masalah riset operasi dalam bentuk persamaan matematika. Model matematika tersebut berfungsi sebagai abstraksi dari masalah nyata yang memudahkan analisis dan pengambilan keputusan. Model matematika dalam riset operasi umumnya terdiri dari variabel, batasan, dan fungsi tujuan.
- Variabel: Merupakan kuantitas yang ingin diukur atau dioptimalkan dalam model.
- Batasan: Merupakan kendala atau syarat yang harus dipenuhi dalam model.
- Fungsi tujuan: Merupakan fungsi matematika yang ingin dioptimalkan (dimaksimalkan atau diminimalkan).
Contoh sederhana:
- Sebuah perusahaan ingin menentukan jumlah produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan.
- Variabel: Jumlah produk A (x) dan jumlah produk B (y).
- Batasan: Mungkin ada batasan sumber daya seperti waktu produksi, bahan baku, atau kapasitas penyimpanan.
- Fungsi tujuan: Keuntungan (Z) yang ingin dimaksimalkan, biasanya didefinisikan sebagai fungsi dari x dan y.
Teknik Penyelesaian Model Riset Operasi
Setelah model matematika dibangun, langkah selanjutnya adalah menyelesaikan model tersebut untuk mendapatkan solusi optimal. Ada berbagai teknik penyelesaian model riset operasi, beberapa di antaranya adalah:
- Metode Simplex: Metode simplex adalah algoritma yang digunakan untuk menyelesaikan masalah program linear, yaitu masalah yang melibatkan fungsi tujuan dan batasan linear. Metode ini secara sistematis mencari solusi optimal dengan mengiterasi melalui titik-titik sudut pada ruang solusi.
- Metode Grafis: Metode grafis digunakan untuk menyelesaikan masalah program linear dengan dua variabel. Metode ini melibatkan penggambaran batasan sebagai garis pada diagram dan menentukan titik sudut yang memberikan nilai optimal pada fungsi tujuan.
Contoh Soal Riset Operasi dengan Metode Simplex
Sebuah perusahaan memproduksi dua jenis produk, A dan B. Setiap produk membutuhkan waktu produksi dan bahan baku yang berbeda. Informasi selengkapnya tercantum dalam tabel berikut:
| Produk | Waktu Produksi (jam/unit) | Bahan Baku (kg/unit) | Keuntungan (Rp/unit) |
|---|---|---|---|
| A | 2 | 1 | 10.000 |
| B | 3 | 2 | 15.000 |
Perusahaan memiliki waktu produksi maksimum 120 jam dan bahan baku maksimum 60 kg. Tentukan jumlah produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan!
Penyelesaian:
1. Membuat Model Matematika
- Variabel: x = Jumlah produk A, y = Jumlah produk B
- Batasan:
- Waktu produksi: 2x + 3y ≤ 120
- Bahan baku: x + 2y ≤ 60
- x ≥ 0, y ≥ 0 (jumlah produk tidak boleh negatif)
- Fungsi tujuan: Z = 10.000x + 15.000y (memaksimalkan keuntungan)
2. Metode Simplex
- Metode simplex melibatkan penggunaan tabel simplex untuk mencari solusi optimal. Tabel simplex berisi informasi tentang variabel, batasan, dan nilai fungsi tujuan pada setiap iterasi.
- Proses iterasi dimulai dengan memasukkan batasan ke dalam tabel simplex dan menentukan solusi awal yang feasible.
- Pada setiap iterasi, tabel simplex diubah untuk mencari solusi yang lebih baik hingga mencapai solusi optimal.
3. Solusi Optimal
- Melalui iterasi metode simplex, diperoleh solusi optimal: x = 20, y = 20.
- Artinya, perusahaan harus memproduksi 20 unit produk A dan 20 unit produk B untuk memaksimalkan keuntungan.
- Keuntungan maksimum yang dapat dicapai adalah Z = 10.000(20) + 15.000(20) = Rp 500.000.000.
Penerapan Riset Operasi dalam Manajemen
Riset operasi (RO) merupakan disiplin ilmu yang memanfaatkan metode ilmiah untuk membantu dalam pengambilan keputusan yang optimal. Penerapan RO dalam manajemen dapat meningkatkan efisiensi, efektivitas, dan profitabilitas dalam berbagai aspek operasional bisnis.
Peran Riset Operasi dalam Pengambilan Keputusan Manajemen
Riset operasi memberikan kerangka kerja yang terstruktur untuk menganalisis masalah kompleks, mengidentifikasi solusi yang optimal, dan mengukur dampak dari keputusan yang diambil.
- RO membantu manajemen dalam memahami hubungan antar variabel yang kompleks, seperti biaya, permintaan, dan sumber daya, yang memungkinkan mereka untuk membuat keputusan yang lebih tepat.
- RO menggunakan model matematis untuk mensimulasikan skenario yang berbeda, sehingga manajemen dapat mengevaluasi berbagai opsi dan memilih yang paling menguntungkan.
- RO membantu dalam mengidentifikasi dan mengatasi kendala yang membatasi kinerja operasional, seperti keterbatasan sumber daya atau kapasitas produksi.
Penggunaan Riset Operasi untuk Mengoptimalkan Proses Produksi
Riset operasi dapat digunakan untuk mengoptimalkan proses produksi dengan meningkatkan efisiensi dan meminimalkan biaya.
- RO dapat membantu dalam menentukan penjadwalan produksi yang optimal, dengan mempertimbangkan faktor-faktor seperti permintaan, kapasitas, dan ketersediaan bahan baku.
- RO dapat digunakan untuk mengoptimalkan penempatan sumber daya, seperti tenaga kerja dan mesin, sehingga proses produksi berjalan lebih efisien.
- RO dapat membantu dalam menentukan jumlah optimal produk yang akan diproduksi, dengan mempertimbangkan permintaan pasar dan biaya produksi.
Penggunaan Riset Operasi untuk Mengelola Persediaan
Riset operasi dapat membantu manajemen dalam mengelola persediaan dengan meminimalkan biaya penyimpanan dan mencegah kekurangan persediaan.
- RO dapat digunakan untuk menentukan jumlah optimal persediaan yang harus disimpan, dengan mempertimbangkan faktor-faktor seperti permintaan, biaya penyimpanan, dan biaya kekurangan persediaan.
- RO dapat membantu dalam menentukan waktu yang tepat untuk memesan persediaan, dengan mempertimbangkan faktor-faktor seperti lead time dan biaya pemesanan.
- RO dapat digunakan untuk mengembangkan sistem persediaan yang lebih efektif, seperti sistem persediaan Just-in-Time (JIT) atau sistem persediaan Material Requirements Planning (MRP).
Contoh Soal Riset Operasi
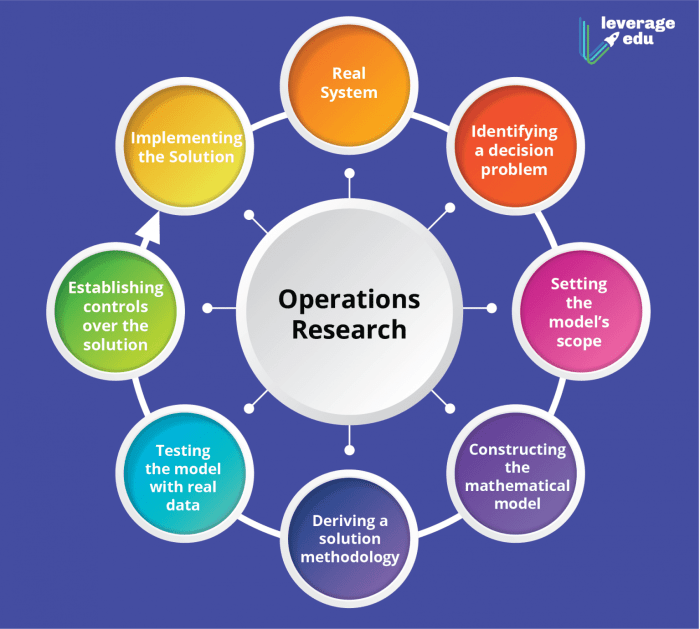
Riset operasi merupakan disiplin ilmu yang menggunakan metode ilmiah untuk memecahkan masalah kompleks dalam pengambilan keputusan. Metode ini menggabungkan teknik matematika, statistik, dan algoritma untuk mengoptimalkan penggunaan sumber daya dan mencapai tujuan yang diinginkan.
Contoh Soal Riset Operasi Berdasarkan Tingkat Kesulitan
Berikut beberapa contoh soal riset operasi dengan tingkat kesulitan yang berbeda:
| Tingkat Kesulitan | Contoh Soal |
|---|---|
| Mudah | Seorang pedagang memiliki 10 kg apel dan 5 kg jeruk. Ia ingin menjual semua buahnya dengan harga termahal. Harga jual apel Rp 10.000 per kg dan jeruk Rp 15.000 per kg. Berapa banyak apel dan jeruk yang harus dijual untuk mendapatkan keuntungan maksimal? |
| Sedang | Sebuah perusahaan manufaktur memproduksi dua jenis produk, A dan B. Produk A membutuhkan 2 jam waktu produksi dan 1 unit bahan baku, sedangkan produk B membutuhkan 3 jam waktu produksi dan 2 unit bahan baku. Perusahaan memiliki 100 jam waktu produksi dan 50 unit bahan baku. Keuntungan per unit produk A adalah Rp 100.000 dan produk B adalah Rp 150.000. Berapa banyak produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan? |
| Sulit | Sebuah perusahaan transportasi memiliki 5 truk dan 10 supir. Setiap truk dapat mengangkut 10 ton barang. Perusahaan ingin mendistribusikan 50 ton barang ke 3 kota dengan biaya transportasi yang minimal. Bagaimana penugasan truk dan supir yang optimal untuk meminimalkan biaya transportasi? |
Contoh Soal Riset Operasi yang Melibatkan Pengambilan Keputusan
Riset operasi sering digunakan untuk membantu dalam pengambilan keputusan yang kompleks. Berikut contohnya:
Sebuah perusahaan ingin meluncurkan produk baru. Mereka memiliki dua pilihan strategi pemasaran: strategi A dan strategi B. Strategi A membutuhkan biaya lebih tinggi tetapi diprediksi akan menghasilkan keuntungan yang lebih besar. Strategi B membutuhkan biaya lebih rendah tetapi diprediksi akan menghasilkan keuntungan yang lebih kecil. Perusahaan ingin memilih strategi pemasaran yang optimal berdasarkan analisis risiko dan keuntungan.
Dalam contoh ini, riset operasi dapat digunakan untuk menganalisis risiko dan keuntungan dari setiap strategi pemasaran. Metode yang dapat digunakan adalah analisis keputusan, yang melibatkan pembuatan pohon keputusan dan perhitungan nilai harapan untuk setiap pilihan.
Contoh Soal Riset Operasi yang Melibatkan Optimasi Sumber Daya
Riset operasi juga digunakan untuk mengoptimalkan penggunaan sumber daya yang terbatas. Berikut contohnya:
Sebuah pabrik ingin memaksimalkan produksi produk A dan produk B dengan menggunakan sumber daya yang terbatas. Pabrik memiliki 100 jam waktu produksi, 50 unit bahan baku, dan 20 pekerja. Produk A membutuhkan 2 jam waktu produksi, 1 unit bahan baku, dan 1 pekerja per unit. Produk B membutuhkan 3 jam waktu produksi, 2 unit bahan baku, dan 2 pekerja per unit. Berapa banyak produk A dan B yang harus diproduksi untuk memaksimalkan produksi?
Dalam contoh ini, riset operasi dapat digunakan untuk menentukan jumlah optimal produk A dan B yang harus diproduksi dengan mempertimbangkan kendala waktu produksi, bahan baku, dan tenaga kerja. Metode yang dapat digunakan adalah pemrograman linear, yang melibatkan penyelesaian sistem persamaan linier untuk menemukan solusi optimal.
Penyelesaian Soal Riset Operasi
Riset operasi merupakan disiplin ilmu yang menggunakan pendekatan matematis dan statistik untuk membantu pengambilan keputusan optimal dalam berbagai situasi. Dalam menyelesaikan soal riset operasi, terdapat beberapa langkah umum yang perlu dilakukan, baik dengan menggunakan metode simplex maupun metode grafis.
Langkah-langkah Penyelesaian Soal Riset Operasi
Berikut adalah langkah-langkah umum dalam menyelesaikan soal riset operasi:
- Mendefinisikan masalah: Langkah pertama adalah memahami dengan jelas masalah yang ingin diselesaikan. Hal ini melibatkan identifikasi tujuan, batasan, dan variabel yang terlibat.
- Membangun model matematika: Setelah memahami masalah, langkah selanjutnya adalah merumuskan model matematika yang merepresentasikan masalah tersebut. Model ini terdiri dari fungsi objektif yang ingin dioptimalkan (dimaksimalkan atau diminimalkan) dan kendala-kendala yang membatasi nilai variabel.
- Memecahkan model: Setelah model matematika dibangun, langkah selanjutnya adalah memecahkan model tersebut untuk menemukan solusi optimal. Solusi optimal merupakan nilai variabel yang memenuhi semua kendala dan mengoptimalkan fungsi objektif.
- Menganalisis solusi: Setelah solusi optimal ditemukan, langkah terakhir adalah menganalisis solusi tersebut. Analisis ini melibatkan interpretasi solusi dalam konteks masalah asli dan evaluasi sensitivitas solusi terhadap perubahan parameter model.
Penyelesaian Soal Riset Operasi dengan Metode Simplex
Metode simplex merupakan metode aljabar linier yang digunakan untuk menyelesaikan masalah pemrograman linier. Metode ini bekerja dengan iteratif, yaitu dengan bergerak dari satu solusi yang layak ke solusi yang layak lainnya sampai solusi optimal ditemukan.
Contoh soal riset operasi dan jawabannya bisa jadi terlihat rumit, tapi sebenarnya konsepnya mirip dengan menghitung jarak di peta. Misalnya, kamu mau tahu berapa jarak sebenarnya antara dua kota, kamu bisa gunakan skala peta yang ada di contoh soal skala peta kelas 7.
Nah, konsep skala ini juga diterapkan dalam riset operasi, cuma objeknya bukan peta tapi bisa berupa model produksi, alur distribusi, atau bahkan strategi marketing. Jadi, dengan memahami skala, kamu bisa mengoptimalkan proses dan mencapai tujuan yang lebih efektif.
- Menentukan variabel keputusan: Langkah pertama adalah menentukan variabel keputusan yang akan digunakan dalam model.
- Menentukan fungsi objektif: Langkah selanjutnya adalah menentukan fungsi objektif yang ingin dioptimalkan.
- Menentukan kendala: Langkah selanjutnya adalah menentukan kendala-kendala yang membatasi nilai variabel.
- Membangun tabel simplex: Setelah model matematika didefinisikan, langkah selanjutnya adalah membangun tabel simplex. Tabel ini berisi informasi tentang variabel keputusan, koefisien fungsi objektif, dan koefisien kendala.
- Melakukan iterasi: Setelah tabel simplex dibangun, langkah selanjutnya adalah melakukan iterasi untuk mencari solusi optimal. Iterasi ini melibatkan pemilihan variabel masuk dan keluar dari basis, serta pembaruan nilai variabel.
- Menentukan solusi optimal: Iterasi dilakukan sampai solusi optimal ditemukan. Solusi optimal ditandai dengan semua nilai variabel non-negatif dan nilai fungsi objektif optimal.
Penyelesaian Soal Riset Operasi dengan Metode Grafis
Metode grafis merupakan metode visual yang digunakan untuk menyelesaikan masalah pemrograman linier dengan dua variabel. Metode ini bekerja dengan menggambarkan kendala-kendala sebagai garis pada bidang koordinat dan mencari titik optimal yang terletak pada daerah layak.
- Menentukan variabel keputusan: Langkah pertama adalah menentukan variabel keputusan yang akan digunakan dalam model.
- Menentukan fungsi objektif: Langkah selanjutnya adalah menentukan fungsi objektif yang ingin dioptimalkan.
- Menentukan kendala: Langkah selanjutnya adalah menentukan kendala-kendala yang membatasi nilai variabel.
- Menggambar garis kendala: Setelah kendala didefinisikan, langkah selanjutnya adalah menggambar garis kendala pada bidang koordinat. Setiap garis mewakili satu kendala.
- Menentukan daerah layak: Setelah semua garis kendala digambar, langkah selanjutnya adalah menentukan daerah layak. Daerah layak adalah daerah yang memenuhi semua kendala.
- Mencari titik optimal: Setelah daerah layak ditentukan, langkah selanjutnya adalah mencari titik optimal. Titik optimal adalah titik yang terletak pada daerah layak dan mengoptimalkan fungsi objektif.
Model Riset Operasi: Contoh Soal Riset Operasi Dan Jawabannya
Riset operasi merupakan bidang ilmu yang menggunakan metode kuantitatif untuk memecahkan masalah kompleks dalam berbagai bidang, seperti bisnis, manufaktur, transportasi, dan kesehatan. Model riset operasi adalah representasi matematis dari suatu sistem atau masalah, yang memungkinkan kita untuk menganalisis dan mengoptimalkan sistem tersebut.
Jenis Model Riset Operasi
Model riset operasi dapat dikategorikan menjadi beberapa jenis, tergantung pada sifat masalah yang dihadapi dan metode yang digunakan untuk menyelesaikannya. Beberapa jenis model riset operasi yang umum digunakan adalah:
- Model Linear Programming: Model ini digunakan untuk memecahkan masalah optimasi dengan kendala linier, yang berarti bahwa semua variabel dan fungsi tujuan dalam model tersebut dapat dinyatakan sebagai persamaan linier. Model linear programming sering digunakan untuk memaksimalkan keuntungan atau meminimalkan biaya dalam berbagai situasi, seperti produksi, transportasi, dan penjadwalan.
- Model Integer Programming: Model ini merupakan perluasan dari model linear programming, di mana beberapa atau semua variabel dalam model dibatasi untuk mengambil nilai integer. Model integer programming sering digunakan untuk memecahkan masalah yang melibatkan keputusan diskrit, seperti memilih lokasi pabrik atau mengalokasikan sumber daya ke berbagai proyek.
- Model Network Flow: Model ini digunakan untuk menganalisis dan mengoptimalkan aliran dalam jaringan, seperti aliran barang dalam rantai pasokan, aliran data dalam jaringan komputer, atau aliran air dalam sistem irigasi. Model network flow dapat digunakan untuk menemukan jalur terpendek, aliran maksimum, atau aliran minimum biaya dalam jaringan.
Contoh Penerapan Model Linear Programming
Misalnya, sebuah perusahaan manufaktur ingin memaksimalkan keuntungannya dengan memproduksi dua jenis produk, A dan B. Perusahaan memiliki sumber daya terbatas, seperti bahan baku, tenaga kerja, dan waktu mesin. Setiap produk memerlukan jumlah sumber daya yang berbeda. Model linear programming dapat digunakan untuk menentukan jumlah optimal produk A dan B yang harus diproduksi untuk memaksimalkan keuntungan, dengan mempertimbangkan kendala sumber daya yang tersedia.
Contoh Penerapan Model Integer Programming
Contohnya, sebuah perusahaan ingin membangun beberapa gudang baru untuk melayani pelanggannya di seluruh negara. Perusahaan memiliki beberapa lokasi potensial untuk gudang, dan setiap lokasi memiliki biaya pembangunan dan kapasitas penyimpanan yang berbeda. Model integer programming dapat digunakan untuk menentukan lokasi optimal untuk gudang baru, dengan mempertimbangkan biaya pembangunan, kapasitas penyimpanan, dan jarak ke pelanggan.
Perangkat Lunak Riset Operasi
Riset operasi merupakan disiplin ilmu yang menggunakan metode kuantitatif untuk memecahkan masalah kompleks dalam berbagai bidang, seperti bisnis, industri, dan pemerintahan. Dalam praktiknya, penggunaan perangkat lunak khusus dapat membantu para praktisi riset operasi dalam menyelesaikan masalah secara efisien dan akurat.
Berbagai Perangkat Lunak Riset Operasi
Perangkat lunak riset operasi dirancang untuk membantu menyelesaikan berbagai masalah riset operasi, mulai dari perencanaan produksi dan manajemen inventaris hingga optimasi jaringan dan pengambilan keputusan. Berikut adalah beberapa jenis perangkat lunak yang umum digunakan:
- Perangkat Lunak Pemrograman Linear: Perangkat lunak ini digunakan untuk menyelesaikan masalah pemrograman linear, yang merupakan jenis masalah optimasi matematika yang melibatkan pencarian solusi optimal untuk fungsi objektif dengan batasan linear. Contohnya adalah perangkat lunak seperti LINDO, CPLEX, dan Gurobi. Perangkat lunak ini memiliki kemampuan untuk memecahkan masalah pemrograman linear skala besar dengan cepat dan akurat.
- Perangkat Lunak Simulasi: Perangkat lunak simulasi digunakan untuk mensimulasikan sistem kompleks dan menganalisis perilaku mereka dalam berbagai skenario. Contohnya adalah perangkat lunak seperti Arena, Simul8, dan AnyLogic. Perangkat lunak simulasi membantu para praktisi riset operasi dalam memahami perilaku sistem, mengidentifikasi bottleneck, dan mengevaluasi berbagai strategi.
- Perangkat Lunak Optimasi Heuristik: Perangkat lunak optimasi heuristik digunakan untuk menemukan solusi optimal untuk masalah yang sulit dipecahkan secara analitis. Contohnya adalah perangkat lunak seperti Genetic Algorithm Toolbox, Simulated Annealing Toolbox, dan Tabu Search Toolbox. Perangkat lunak ini memanfaatkan algoritma heuristik untuk menemukan solusi yang baik dalam waktu yang relatif singkat, meskipun tidak selalu optimal.
- Perangkat Lunak Pengambilan Keputusan: Perangkat lunak pengambilan keputusan membantu para praktisi riset operasi dalam mengidentifikasi dan mengevaluasi pilihan yang tersedia, serta memilih solusi terbaik berdasarkan kriteria yang telah ditentukan. Contohnya adalah perangkat lunak seperti Decision-Pro, Expert Choice, dan Analytic Hierarchy Process (AHP) Toolbox. Perangkat lunak ini membantu dalam pengambilan keputusan yang kompleks dan melibatkan banyak faktor.
Contoh Penggunaan Perangkat Lunak Riset Operasi
Berikut adalah beberapa contoh penggunaan perangkat lunak riset operasi dalam kasus nyata:
- Perencanaan Produksi: Perusahaan manufaktur dapat menggunakan perangkat lunak pemrograman linear untuk merencanakan produksi, meminimalkan biaya, dan memenuhi permintaan pelanggan. Misalnya, sebuah perusahaan manufaktur dapat menggunakan perangkat lunak ini untuk menentukan jumlah produk yang harus diproduksi untuk setiap jenis produk, dengan mempertimbangkan keterbatasan kapasitas produksi, bahan baku, dan tenaga kerja.
- Manajemen Inventaris: Perangkat lunak simulasi dapat digunakan untuk mengoptimalkan manajemen inventaris, meminimalkan biaya penyimpanan, dan menghindari kekurangan persediaan. Misalnya, sebuah perusahaan ritel dapat menggunakan perangkat lunak simulasi untuk menganalisis dampak perubahan kebijakan inventaris terhadap tingkat persediaan, biaya penyimpanan, dan tingkat layanan pelanggan.
- Optimasi Jaringan: Perangkat lunak optimasi heuristik dapat digunakan untuk mengoptimalkan jaringan transportasi, meminimalkan biaya transportasi, dan meningkatkan efisiensi pengiriman. Misalnya, sebuah perusahaan logistik dapat menggunakan perangkat lunak ini untuk menentukan rute pengiriman yang optimal, dengan mempertimbangkan jarak, waktu tempuh, dan kapasitas kendaraan.
- Pengambilan Keputusan Strategis: Perangkat lunak pengambilan keputusan dapat digunakan untuk membantu perusahaan dalam membuat keputusan strategis, seperti investasi, pengembangan produk, dan strategi pemasaran. Misalnya, sebuah perusahaan dapat menggunakan perangkat lunak ini untuk mengevaluasi berbagai strategi pemasaran dan memilih strategi yang paling efektif untuk mencapai target pasar.
Daftar Perangkat Lunak Riset Operasi, Contoh soal riset operasi dan jawabannya
Berikut adalah tabel yang berisi daftar perangkat lunak riset operasi dengan fitur dan keunggulan masing-masing:
| Nama Perangkat Lunak | Fitur Utama | Keunggulan |
|---|---|---|
| LINDO | Pemrograman linear, integer programming, non-linear programming | Mudah digunakan, antarmuka yang ramah pengguna, kemampuan untuk memecahkan masalah skala besar |
| CPLEX | Pemrograman linear, integer programming, non-linear programming, mixed-integer programming | Kinerja tinggi, kemampuan untuk memecahkan masalah yang sangat kompleks, dukungan untuk berbagai format data |
| Gurobi | Pemrograman linear, integer programming, non-linear programming, mixed-integer programming | Kinerja tinggi, kemampuan untuk memecahkan masalah yang sangat kompleks, dukungan untuk berbagai format data |
| Arena | Simulasi sistem diskrit, simulasi sistem kontinu, simulasi berbasis agen | Antarmuka yang ramah pengguna, kemampuan untuk membangun model simulasi yang kompleks, dukungan untuk berbagai jenis analisis |
| Simul8 | Simulasi sistem diskrit, simulasi sistem kontinu, simulasi berbasis agen | Kinerja tinggi, kemampuan untuk memecahkan masalah yang sangat kompleks, dukungan untuk berbagai format data |
| AnyLogic | Simulasi sistem diskrit, simulasi sistem kontinu, simulasi berbasis agen | Kinerja tinggi, kemampuan untuk memecahkan masalah yang sangat kompleks, dukungan untuk berbagai format data |
| Genetic Algorithm Toolbox | Algoritma genetika, optimasi heuristik | Mudah digunakan, kemampuan untuk memecahkan masalah yang kompleks, dukungan untuk berbagai jenis masalah |
| Simulated Annealing Toolbox | Simulated annealing, optimasi heuristik | Mudah digunakan, kemampuan untuk memecahkan masalah yang kompleks, dukungan untuk berbagai jenis masalah |
| Tabu Search Toolbox | Tabu search, optimasi heuristik | Mudah digunakan, kemampuan untuk memecahkan masalah yang kompleks, dukungan untuk berbagai jenis masalah |
| Decision-Pro | Pengambilan keputusan, analisis risiko, analisis sensitivitas | Antarmuka yang ramah pengguna, kemampuan untuk membangun model pengambilan keputusan yang kompleks, dukungan untuk berbagai jenis analisis |
| Expert Choice | Analytic Hierarchy Process (AHP), pengambilan keputusan multi-kriteria | Antarmuka yang ramah pengguna, kemampuan untuk membangun model pengambilan keputusan yang kompleks, dukungan untuk berbagai jenis analisis |
| Analytic Hierarchy Process (AHP) Toolbox | Analytic Hierarchy Process (AHP), pengambilan keputusan multi-kriteria | Antarmuka yang ramah pengguna, kemampuan untuk membangun model pengambilan keputusan yang kompleks, dukungan untuk berbagai jenis analisis |
Tren dan Perkembangan Riset Operasi
Riset operasi merupakan bidang ilmu yang mempelajari penggunaan metode ilmiah untuk menyelesaikan masalah kompleks, khususnya yang melibatkan pengambilan keputusan. Bidang ini telah mengalami perkembangan pesat selama beberapa dekade terakhir, seiring dengan munculnya teknologi baru dan kompleksitas masalah yang dihadapi oleh berbagai sektor.
Perkembangan Riset Operasi di Era Digital
Perkembangan teknologi digital telah membuka peluang baru dalam riset operasi. Kehadiran data besar (big data) memungkinkan pengambilan keputusan yang lebih akurat dan efisien. Data besar dapat dianalisis menggunakan algoritma canggih, seperti machine learning dan deep learning, untuk mengidentifikasi pola dan tren yang tidak terlihat sebelumnya.
- Algoritma Optimasi: Algoritma optimasi yang canggih, seperti algoritma genetika dan simulated annealing, dapat digunakan untuk menemukan solusi optimal untuk masalah kompleks yang melibatkan banyak variabel.
- Simulasi: Simulasi komputer memungkinkan peneliti untuk mensimulasikan berbagai skenario dan menguji berbagai strategi, membantu dalam pengambilan keputusan yang lebih tepat.
- Analisis Prediktif: Teknik analisis prediktif, seperti time series analysis dan machine learning, dapat digunakan untuk memprediksi tren dan pola masa depan, membantu dalam pengambilan keputusan yang lebih proaktif.
Penerapan Riset Operasi dalam Mengatasi Masalah di Era Digital
Riset operasi memiliki peran penting dalam mengatasi berbagai masalah di era digital, seperti:
- Optimasi Rantai Pasokan: Riset operasi dapat digunakan untuk mengoptimalkan rantai pasokan, mulai dari perencanaan produksi hingga distribusi, dengan mempertimbangkan faktor-faktor seperti biaya, waktu, dan permintaan.
- Manajemen Risiko: Riset operasi dapat digunakan untuk mengidentifikasi dan menilai risiko, serta mengembangkan strategi mitigasi risiko yang efektif.
- Pengambilan Keputusan Bisnis: Riset operasi dapat digunakan untuk mendukung pengambilan keputusan bisnis, seperti penentuan harga, pemilihan investasi, dan strategi pemasaran.
- Personalisasi Layanan: Riset operasi dapat digunakan untuk mempersonalisasi layanan pelanggan, seperti rekomendasi produk dan layanan yang disesuaikan dengan kebutuhan individu.
Riset Operasi dalam Mendukung Program Sustainable Development Goals (SDGs)
Riset operasi dapat digunakan untuk mendukung program Sustainable Development Goals (SDGs) dengan membantu dalam mengoptimalkan sumber daya dan menemukan solusi yang berkelanjutan.
- Pengelolaan Sumber Daya: Riset operasi dapat digunakan untuk mengoptimalkan penggunaan sumber daya alam, seperti air dan energi, serta mengurangi limbah.
- Perencanaan Kota: Riset operasi dapat digunakan untuk merancang sistem transportasi yang efisien, mengurangi kemacetan, dan meningkatkan kualitas hidup perkotaan.
- Penanggulangan Bencana: Riset operasi dapat digunakan untuk mengembangkan strategi penanggulangan bencana yang efektif, seperti sistem peringatan dini dan manajemen evakuasi.
- Pengurangan Kemiskinan: Riset operasi dapat digunakan untuk mengoptimalkan program bantuan sosial, meningkatkan akses terhadap pendidikan dan kesehatan, dan mendorong pertumbuhan ekonomi yang inklusif.
Pemungkas
Mempelajari contoh soal riset operasi dan jawabannya adalah langkah awal yang penting untuk memahami dan menguasai konsep-konsep riset operasi. Dengan memahami teknik dasar, model-model yang digunakan, dan langkah-langkah penyelesaian soal, Anda dapat mengoptimalkan pengambilan keputusan dan meraih hasil yang lebih baik dalam berbagai bidang kehidupan.