Contoh soal rotasi terhadap titik pusat 0 0 – Pernahkah kamu membayangkan bagaimana sebuah titik atau objek bisa berputar di sekitar titik tertentu? Rotasi terhadap titik pusat (0,0) merupakan salah satu konsep penting dalam geometri yang membahas tentang perputaran titik atau objek di sekitar titik pusat (0,0) dengan sudut tertentu. Bayangkan seperti jarum jam yang berputar, hanya saja titik pusatnya adalah titik (0,0) pada koordinat kartesius.
Rotasi ini ternyata memiliki peran penting dalam berbagai bidang, mulai dari seni, desain, hingga teknologi. Kamu mungkin pernah melihat animasi atau gambar yang diputar, atau bahkan desain logo yang menggunakan konsep rotasi. Di dalam dunia matematika, rotasi juga memiliki aplikasi yang luas dalam geometri, aljabar linear, dan kalkulus.
Pengertian Rotasi Terhadap Titik Pusat (0,0)
Rotasi terhadap titik pusat (0,0) merupakan transformasi geometri yang memutar suatu titik atau bangun geometri terhadap titik pusat (0,0) dengan sudut tertentu. Dalam rotasi, jarak titik ke titik pusat tetap sama, tetapi posisinya berubah sesuai dengan sudut rotasi.
Ilustrasi Rotasi Terhadap Titik Pusat (0,0)
Bayangkan sebuah titik A (2, 1) yang akan dirotasi 90 derajat searah jarum jam terhadap titik pusat (0,0). Setelah rotasi, titik A akan berpindah ke posisi A’ (-1, 2). Perhatikan bahwa jarak titik A ke titik pusat (0,0) tetap sama dengan jarak titik A’ ke titik pusat (0,0).
Ilustrasi rotasi dapat digambarkan dengan diagram seperti berikut:
[Gambar ilustrasi titik A (2,1) dirotasi 90 derajat searah jarum jam terhadap titik pusat (0,0) menjadi A’ (-1, 2). Titik A dan A’ memiliki jarak yang sama ke titik pusat (0,0).]
Jenis-Jenis Rotasi Terhadap Titik Pusat (0,0)
Rotasi terhadap titik pusat (0,0) dapat diklasifikasikan berdasarkan sudut rotasi dan arahnya. Berikut adalah beberapa jenis rotasi yang umum:
| Jenis Rotasi | Sudut Rotasi | Contoh Ilustrasi |
|---|---|---|
| Rotasi 90 derajat searah jarum jam | 90 derajat | [Gambar ilustrasi titik A (2,1) dirotasi 90 derajat searah jarum jam terhadap titik pusat (0,0) menjadi A’ (-1, 2). Titik A dan A’ memiliki jarak yang sama ke titik pusat (0,0).] |
| Rotasi 90 derajat berlawanan arah jarum jam | 90 derajat | [Gambar ilustrasi titik A (2,1) dirotasi 90 derajat berlawanan arah jarum jam terhadap titik pusat (0,0) menjadi A’ (1, -2). Titik A dan A’ memiliki jarak yang sama ke titik pusat (0,0).] |
| Rotasi 180 derajat | 180 derajat | [Gambar ilustrasi titik A (2,1) dirotasi 180 derajat terhadap titik pusat (0,0) menjadi A’ (-2, -1). Titik A dan A’ memiliki jarak yang sama ke titik pusat (0,0).] |
| Rotasi 270 derajat searah jarum jam | 270 derajat | [Gambar ilustrasi titik A (2,1) dirotasi 270 derajat searah jarum jam terhadap titik pusat (0,0) menjadi A’ (1, -2). Titik A dan A’ memiliki jarak yang sama ke titik pusat (0,0).] |
| Rotasi 270 derajat berlawanan arah jarum jam | 270 derajat | [Gambar ilustrasi titik A (2,1) dirotasi 270 derajat berlawanan arah jarum jam terhadap titik pusat (0,0) menjadi A’ (-1, 2). Titik A dan A’ memiliki jarak yang sama ke titik pusat (0,0).] |
Rumus Rotasi Terhadap Titik Pusat (0,0)
Rotasi merupakan transformasi geometri yang memindahkan titik atau bangun geometri di sekitar titik pusat tertentu dengan sudut tertentu. Dalam kasus rotasi terhadap titik pusat (0,0), titik-titik pada bidang Cartesian diputar dengan sudut θ terhadap titik asal. Untuk memahami rumus rotasi, kita perlu memahami hubungannya dengan trigonometri.
Rumus Rotasi
Rumus umum untuk rotasi titik (x,y) terhadap titik pusat (0,0) dengan sudut θ adalah:
x’ = x cos θ – y sin θ
y’ = x sin θ + y cos θ
di mana:
- (x,y) adalah koordinat titik awal
- (x’,y’) adalah koordinat titik setelah diputar
- θ adalah sudut rotasi
Hubungan dengan Trigonometri
Rumus rotasi ini didasarkan pada konsep trigonometri, khususnya lingkaran satuan. Bayangkan titik (x,y) pada lingkaran satuan. Jika kita putar titik tersebut dengan sudut θ, maka koordinat titik baru (x’,y’) dapat dihitung dengan menggunakan fungsi sinus dan cosinus.
Dalam lingkaran satuan, cos θ adalah proyeksi titik (x,y) ke sumbu x, sedangkan sin θ adalah proyeksi titik (x,y) ke sumbu y. Dengan menggunakan rumus rotasi, kita dapat menghitung koordinat baru (x’,y’) berdasarkan proyeksi titik (x,y) ke sumbu x dan y.
Contoh Penerapan
Misalnya, kita ingin memutar titik (2,3) sebesar 90 derajat berlawanan arah jarum jam terhadap titik pusat (0,0).
Maka, kita dapat menerapkan rumus rotasi dengan θ = 90 derajat:
x’ = 2 cos 90° – 3 sin 90° = -3
y’ = 2 sin 90° + 3 cos 90° = 2
Jadi, koordinat titik setelah diputar adalah (-3,2).
Contoh Soal Rotasi Terhadap Titik Pusat (0,0)
Pada pembahasan sebelumnya, telah dijelaskan tentang konsep rotasi terhadap titik pusat (0,0) dan rumus yang digunakan untuk menentukan hasil rotasi titik. Sekarang, mari kita bahas beberapa contoh soal untuk mengasah pemahaman Anda tentang konsep rotasi.
Rotasi Titik
Misalkan kita ingin merotasi titik (a,b) terhadap titik pusat (0,0) dengan sudut θ. Rumus rotasi yang digunakan adalah:
(x’, y’) = (a cos θ – b sin θ, a sin θ + b cos θ)
Untuk menyelesaikan soal rotasi titik, Anda perlu mengganti nilai a, b, dan θ ke dalam rumus tersebut.
Contoh Soal Rotasi Segitiga
Misalkan kita memiliki segitiga dengan titik-titik sudut A(2,1), B(4,3), dan C(1,5). Tentukan koordinat titik-titik sudut segitiga setelah dirotasi 90 derajat berlawanan arah jarum jam terhadap titik pusat (0,0).
Untuk menyelesaikan soal ini, kita perlu merotasi setiap titik sudut segitiga tersebut dengan menggunakan rumus rotasi. Berikut langkah-langkahnya:
- Tentukan nilai θ, yaitu 90 derajat.
- Hitung koordinat titik A’ setelah dirotasi:
- x’ = 2 cos 90° – 1 sin 90° = -1
- y’ = 2 sin 90° + 1 cos 90° = 2
- Hitung koordinat titik B’ setelah dirotasi:
- x’ = 4 cos 90° – 3 sin 90° = -3
- y’ = 4 sin 90° + 3 cos 90° = 4
- Hitung koordinat titik C’ setelah dirotasi:
- x’ = 1 cos 90° – 5 sin 90° = -5
- y’ = 1 sin 90° + 5 cos 90° = 1
- Jadi, koordinat titik-titik sudut segitiga setelah dirotasi adalah A'(-1,2), B'(-3,4), dan C'(-5,1).
Contoh Soal Rotasi Persegi Panjang
Misalkan kita memiliki persegi panjang dengan titik-titik sudut P(1,1), Q(4,1), R(4,3), dan S(1,3). Tentukan koordinat titik-titik sudut persegi panjang setelah dirotasi 180 derajat terhadap titik pusat (0,0).
Contoh soal rotasi terhadap titik pusat (0, 0) biasanya melibatkan menentukan koordinat bayangan suatu titik setelah diputar dengan sudut tertentu. Misalnya, titik A(2, 3) diputar 90 derajat searah jarum jam. Nah, untuk menyelesaikannya, kita perlu memahami konsep trigonometri dan fungsi naik-turunnya.
Contoh soal fungsi naik dan fungsi turun trigonometri bisa membantu kita memahami bagaimana menentukan nilai sinus, cosinus, dan tangen pada sudut tertentu. Dengan menguasai konsep ini, kita dapat dengan mudah menentukan koordinat bayangan titik A setelah dirotasi.
Langkah-langkahnya sama seperti contoh soal segitiga. Kita perlu merotasi setiap titik sudut persegi panjang dengan menggunakan rumus rotasi:
- Tentukan nilai θ, yaitu 180 derajat.
- Hitung koordinat titik P’ setelah dirotasi:
- x’ = 1 cos 180° – 1 sin 180° = -1
- y’ = 1 sin 180° + 1 cos 180° = -1
- Hitung koordinat titik Q’ setelah dirotasi:
- x’ = 4 cos 180° – 1 sin 180° = -4
- y’ = 4 sin 180° + 1 cos 180° = -1
- Hitung koordinat titik R’ setelah dirotasi:
- x’ = 4 cos 180° – 3 sin 180° = -4
- y’ = 4 sin 180° + 3 cos 180° = -3
- Hitung koordinat titik S’ setelah dirotasi:
- x’ = 1 cos 180° – 3 sin 180° = -1
- y’ = 1 sin 180° + 3 cos 180° = -3
- Jadi, koordinat titik-titik sudut persegi panjang setelah dirotasi adalah P'(-1,-1), Q'(-4,-1), R'(-4,-3), dan S'(-1,-3).
Penerapan Rotasi Terhadap Titik Pusat (0,0)
Rotasi terhadap titik pusat (0,0) merupakan konsep fundamental dalam geometri yang memiliki aplikasi luas dalam berbagai bidang, mulai dari seni dan desain hingga teknologi. Penerapannya memungkinkan kita untuk memanipulasi objek dan menciptakan efek visual yang menarik.
Penerapan dalam Seni dan Desain
Dalam seni dan desain, rotasi terhadap titik pusat (0,0) digunakan untuk menciptakan pola, motif, dan efek simetris. Misalnya, dalam seni kaligrafi, rotasi digunakan untuk menghasilkan bentuk-bentuk huruf yang rumit dan unik. Desainer grafis juga menggunakan rotasi untuk membuat logo, ikon, dan elemen visual lainnya yang menarik perhatian.
- Rotasi 90 derajat pada sebuah persegi panjang akan menghasilkan sebuah persegi.
- Rotasi 180 derajat pada sebuah lingkaran akan menghasilkan lingkaran yang sama.
Penerapan dalam Teknologi
Dalam teknologi, rotasi terhadap titik pusat (0,0) memiliki peran penting dalam pemrosesan gambar, animasi, dan simulasi. Perangkat lunak pengolah gambar memanfaatkan rotasi untuk memutar, memiringkan, atau mengubah orientasi gambar. Dalam animasi, rotasi digunakan untuk menciptakan gerakan yang realistis pada objek 3D.
- Dalam pemrograman komputer, fungsi rotasi dapat diterapkan pada objek 2D atau 3D, seperti dalam game, desain grafis, dan aplikasi simulasi.
- Rotasi digunakan dalam pemrosesan gambar untuk mengubah orientasi gambar, misalnya, memutar gambar 90 derajat atau 180 derajat.
Keterkaitan dengan Transformasi Geometri Lainnya
Rotasi terhadap titik pusat (0,0) merupakan salah satu dari empat transformasi geometri dasar, yaitu rotasi, translasi, refleksi, dan dilatasi. Transformasi geometri lainnya dapat dikombinasikan dengan rotasi untuk menghasilkan efek visual yang lebih kompleks. Misalnya, translasi dan rotasi dapat digunakan bersamaan untuk memindahkan dan memutar objek secara simultan.
Rotasi terhadap titik pusat (0,0) merupakan transformasi isometri, yang berarti bahwa jarak antara dua titik tetap sama setelah rotasi.
Sifat-sifat Rotasi Terhadap Titik Pusat (0,0)
Rotasi terhadap titik pusat (0,0) merupakan transformasi geometri yang memutar setiap titik pada bidang terhadap titik pusat (0,0) dengan sudut tertentu. Transformasi ini memiliki beberapa sifat penting yang mempengaruhi hasil rotasi terhadap objek geometri.
Kekekalan Jarak
Salah satu sifat penting dari rotasi terhadap titik pusat (0,0) adalah kekekalan jarak. Artinya, jarak antara dua titik pada objek geometri akan tetap sama setelah dilakukan rotasi. Hal ini karena rotasi hanya mengubah posisi titik-titik, tetapi tidak mengubah jarak relatif antara mereka.
Kekekalan Sudut
Selain kekekalan jarak, rotasi terhadap titik pusat (0,0) juga memiliki sifat kekekalan sudut. Sudut antara dua garis atau dua segmen garis pada objek geometri akan tetap sama setelah dilakukan rotasi. Ini berarti bahwa bentuk dan ukuran objek geometri akan tetap sama setelah rotasi, hanya saja posisinya yang berubah.
Tabel Sifat Rotasi
| Sifat | Contoh |
|---|---|
| Kekekalan Jarak | Misalnya, jika kita memutar segitiga ABC dengan titik pusat (0,0) sebesar 90 derajat, maka jarak antara titik A dan titik B, titik B dan titik C, serta titik C dan titik A akan tetap sama setelah rotasi. |
| Kekekalan Sudut | Jika kita memutar persegi ABCD dengan titik pusat (0,0) sebesar 45 derajat, maka sudut-sudut persegi, yaitu 90 derajat, akan tetap sama setelah rotasi. |
Rotasi Terhadap Titik Pusat (0,0) dengan Sudut Berbeda
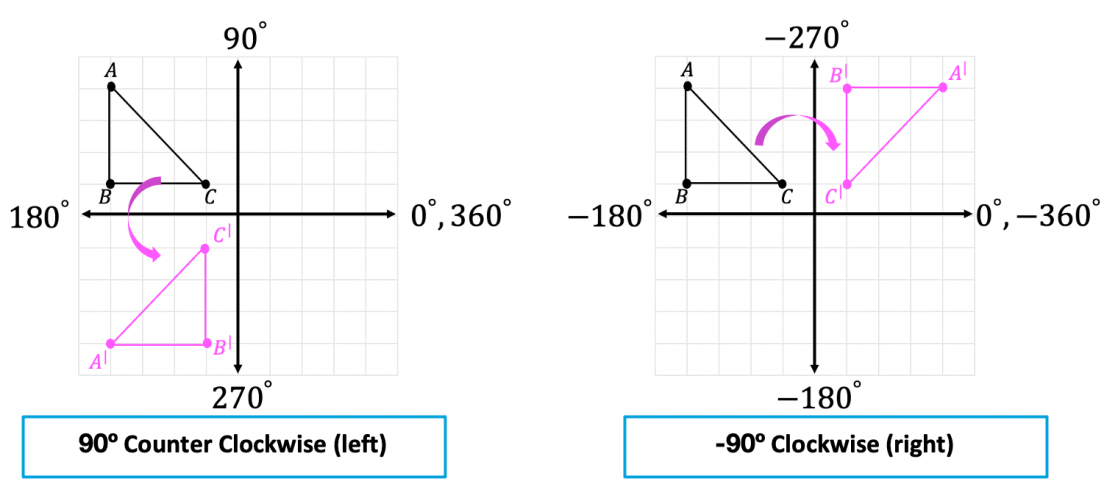
Rotasi terhadap titik pusat (0,0) merupakan transformasi geometri yang memutar suatu titik atau bangun geometri terhadap titik pusat (0,0) dengan sudut tertentu. Sudut rotasi dapat bernilai positif atau negatif, yang menunjukkan arah rotasi, yaitu berlawanan arah jarum jam (positif) atau searah jarum jam (negatif).
Rumus Rotasi untuk Sudut Khusus
Untuk sudut-sudut khusus seperti 90 derajat, 180 derajat, dan 270 derajat, terdapat rumus rotasi yang lebih sederhana. Berikut adalah rumus-rumus tersebut:
- Rotasi 90 derajat: (x, y) diputar menjadi (-y, x)
- Rotasi 180 derajat: (x, y) diputar menjadi (-x, -y)
- Rotasi 270 derajat: (x, y) diputar menjadi (y, -x)
Contoh Soal Rotasi dengan Sudut Khusus
Misalkan titik A(2, 3) dirotasikan terhadap titik pusat (0, 0) dengan sudut 90 derajat. Tentukan koordinat bayangan titik A.
- Tentukan rumus rotasi untuk sudut 90 derajat: (x, y) diputar menjadi (-y, x).
- Terapkan rumus pada titik A(2, 3): (-3, 2).
- Jadi, koordinat bayangan titik A adalah (-3, 2).
Diagram Rotasi Titik (x,y) terhadap Titik Pusat (0,0)
Berikut adalah diagram yang menunjukkan hasil rotasi titik (x, y) terhadap titik pusat (0, 0) dengan sudut 90 derajat, 180 derajat, dan 270 derajat:
Rotasi 90 derajat: Titik (x, y) diputar 90 derajat berlawanan arah jarum jam menjadi titik (-y, x). Bayangkan titik (x, y) bergerak searah jarum jam hingga membentuk sudut 90 derajat terhadap titik pusat (0, 0). Titik hasil rotasi berada di kuadran yang berbeda dengan titik awal, yaitu jika titik awal di kuadran I, maka titik hasil rotasi berada di kuadran II.
Rotasi 180 derajat: Titik (x, y) diputar 180 derajat berlawanan arah jarum jam menjadi titik (-x, -y). Bayangkan titik (x, y) bergerak searah jarum jam hingga membentuk sudut 180 derajat terhadap titik pusat (0, 0). Titik hasil rotasi berada di kuadran yang berlawanan dengan titik awal, yaitu jika titik awal di kuadran I, maka titik hasil rotasi berada di kuadran III.
Rotasi 270 derajat: Titik (x, y) diputar 270 derajat berlawanan arah jarum jam menjadi titik (y, -x). Bayangkan titik (x, y) bergerak searah jarum jam hingga membentuk sudut 270 derajat terhadap titik pusat (0, 0). Titik hasil rotasi berada di kuadran yang berbeda dengan titik awal, yaitu jika titik awal di kuadran I, maka titik hasil rotasi berada di kuadran IV.
Rotasi Terhadap Titik Pusat (0,0) dalam Koordinat Kartesius
Rotasi terhadap titik pusat (0,0) dalam koordinat kartesius merupakan transformasi geometri yang memutar suatu titik atau bangun geometri terhadap titik asal (0,0) dengan sudut tertentu. Proses rotasi ini akan menghasilkan titik atau bangun geometri baru yang memiliki bentuk dan ukuran yang sama dengan titik atau bangun geometri awal, namun posisinya berubah.
Cara Melakukan Rotasi Terhadap Titik Pusat (0,0)
Untuk melakukan rotasi terhadap titik pusat (0,0), kita dapat menggunakan rumus rotasi berikut:
x’ = x cos θ – y sin θ
y’ = x sin θ + y cos θ
di mana:
- (x, y) adalah koordinat titik awal
- (x’, y’) adalah koordinat titik hasil rotasi
- θ adalah sudut rotasi
Rumus ini didasarkan pada konsep trigonometri dan hubungan antara koordinat kartesius dengan sudut. Dengan menggunakan rumus ini, kita dapat menentukan koordinat titik hasil rotasi dengan mudah.
Contoh Soal Rotasi Titik (x,y) Terhadap Titik Pusat (0,0)
Misalnya, kita ingin merotasi titik (2, 3) terhadap titik pusat (0,0) dengan sudut 90 derajat. Maka, kita dapat menggunakan rumus rotasi di atas:
x’ = 2 cos 90° – 3 sin 90° = -3
y’ = 2 sin 90° + 3 cos 90° = 2
Jadi, titik (2, 3) setelah dirotasi 90 derajat terhadap titik pusat (0,0) akan menjadi titik (-3, 2).
Tabel Koordinat Titik Awal dan Titik Hasil Rotasi
| Titik Awal (x, y) | Sudut Rotasi (θ) | Titik Hasil Rotasi (x’, y’) |
|---|---|---|
| (2, 3) | 90° | (-3, 2) |
| (1, 1) | 180° | (-1, -1) |
| (-2, 4) | 270° | (4, 2) |
Tabel di atas menunjukkan contoh koordinat titik awal dan titik hasil rotasi setelah diputar terhadap titik pusat (0,0) dengan sudut tertentu. Dengan memahami konsep rotasi terhadap titik pusat (0,0) dan menggunakan rumus rotasi, kita dapat menentukan koordinat titik hasil rotasi dengan mudah.
Rotasi Terhadap Titik Pusat (0,0) dalam Vektor
Rotasi dalam vektor merupakan transformasi geometri yang mengubah posisi suatu vektor dengan memutarnya terhadap suatu titik pusat tertentu. Dalam konteks ini, kita akan membahas rotasi terhadap titik pusat (0,0), yang merupakan titik asal dalam sistem koordinat kartesius.
Rotasi Vektor Terhadap Titik Pusat (0,0), Contoh soal rotasi terhadap titik pusat 0 0
Rotasi vektor terhadap titik pusat (0,0) dapat dilakukan dengan menggunakan konsep perkalian matriks. Matriks rotasi yang digunakan untuk memutar vektor (a, b) dengan sudut θ terhadap titik pusat (0,0) adalah:
[cos θ -sin θ]
[sin θ cos θ]
Hasil rotasi vektor (a, b) terhadap titik pusat (0,0) dengan sudut θ dapat diperoleh dengan mengalikan matriks rotasi dengan vektor (a, b).
Hasil rotasi vektor dapat dihitung sebagai berikut:
[cos θ -sin θ] [a] = [a cos θ – b sin θ]
[sin θ cos θ] [b] [a sin θ + b cos θ]
Jadi, vektor (a, b) setelah dirotasi dengan sudut θ terhadap titik pusat (0,0) menjadi vektor (a cos θ – b sin θ, a sin θ + b cos θ).
Contoh Soal Rotasi Vektor
Misalkan kita memiliki vektor (2, 3) yang ingin dirotasi dengan sudut 45° terhadap titik pusat (0,0).
Langkah-langkah untuk menyelesaikan soal ini adalah:
- Tentukan matriks rotasi dengan sudut θ = 45°.
- Kalikan matriks rotasi dengan vektor (2, 3).
- Hasil perkalian matriks adalah vektor baru yang merupakan hasil rotasi vektor (2, 3) terhadap titik pusat (0,0) dengan sudut 45°.
Matriks rotasi dengan sudut 45° adalah:
[cos 45° -sin 45°]
[sin 45° cos 45°]
Hasil perkalian matriks rotasi dengan vektor (2, 3) adalah:
[cos 45° -sin 45°] [2] = [2 cos 45° – 3 sin 45°] ≈ [ -0.71 ]
[sin 45° cos 45°] [3] [2 sin 45° + 3 cos 45°] ≈ [ 3.54 ]
Jadi, hasil rotasi vektor (2, 3) terhadap titik pusat (0,0) dengan sudut 45° adalah vektor (-0.71, 3.54).
Diagram Ilustrasi Rotasi Vektor
Untuk menggambarkan hasil rotasi vektor dalam diagram, kita dapat menggunakan sistem koordinat kartesius.
Gambarlah vektor awal (2, 3) dan titik pusat (0, 0) pada sistem koordinat kartesius. Kemudian, putar vektor (2, 3) dengan sudut 45° terhadap titik pusat (0, 0). Hasil rotasi vektor akan menjadi vektor (-0.71, 3.54).
Diagram ini menunjukkan bahwa vektor (2, 3) telah dirotasi dengan sudut 45° terhadap titik pusat (0, 0) dan menghasilkan vektor baru (-0.71, 3.54).
Rotasi Terhadap Titik Pusat (0,0) dalam Persamaan Linear: Contoh Soal Rotasi Terhadap Titik Pusat 0 0
Rotasi terhadap titik pusat (0,0) merupakan transformasi geometri yang memutar setiap titik pada bidang terhadap titik asal (0,0) dengan sudut tertentu. Transformasi ini dapat diterapkan pada persamaan linear, dan akan mengubah bentuk persamaan tersebut.
Pengaruh Rotasi terhadap Persamaan Linear
Rotasi terhadap titik pusat (0,0) pada persamaan linear akan mengubah posisi garis yang direpresentasikan oleh persamaan tersebut. Sudut rotasi menentukan sejauh mana garis tersebut berputar.
Contoh Persamaan Linear dan Rotasi
Misalkan kita memiliki persamaan linear y = x. Persamaan ini merepresentasikan garis lurus yang melewati titik asal dan memiliki kemiringan 1. Jika kita memutar garis ini 90 derajat searah jarum jam terhadap titik pusat (0,0), maka persamaan garis tersebut akan berubah menjadi x = -y.
- Persamaan awal: y = x
- Rotasi 90 derajat searah jarum jam: x = -y
Perubahan ini dapat dijelaskan dengan memahami bagaimana rotasi mempengaruhi koordinat titik pada garis. Setiap titik (x, y) pada garis y = x akan diputar 90 derajat searah jarum jam, menghasilkan titik baru (-y, x). Jika kita substitusikan koordinat baru ini ke dalam persamaan awal, kita akan mendapatkan x = -y.
Hubungan Rotasi dengan Transformasi Geometri Lainnya
Rotasi terhadap titik pusat (0,0) dapat dikombinasikan dengan transformasi geometri lainnya seperti translasi dan refleksi untuk menghasilkan transformasi yang lebih kompleks. Misalnya, jika kita mentranslasikan garis y = x sebesar 2 satuan ke kanan, kemudian memutarnya 90 derajat searah jarum jam terhadap titik pusat (0,0), maka kita akan mendapatkan garis baru dengan persamaan x = -y + 2.
- Translasi 2 satuan ke kanan: y = x + 2
- Rotasi 90 derajat searah jarum jam: x = -y + 2
Dengan menggabungkan berbagai transformasi geometri, kita dapat menghasilkan berbagai bentuk dan posisi garis baru dari persamaan linear awal.
Rotasi Terhadap Titik Pusat (0,0) dalam Transformasi Geometri
Rotasi terhadap titik pusat (0,0) merupakan salah satu transformasi geometri yang mengubah posisi suatu titik atau bangun geometri dengan memutarnya terhadap titik pusat (0,0) pada bidang kartesius. Dalam transformasi ini, bentuk dan ukuran bangun geometri tetap sama, hanya posisinya yang berubah. Rotasi dapat didefinisikan dengan sudut putar dan arah putaran, yang menentukan sejauh mana dan ke mana bangun geometri diputar.
Jenis-Jenis Transformasi Geometri
Transformasi geometri merupakan proses perubahan posisi, bentuk, dan ukuran suatu bangun geometri. Selain rotasi, terdapat beberapa jenis transformasi geometri lainnya, yaitu:
- Translasi: Pergeseran suatu bangun geometri ke arah tertentu dengan jarak tertentu. Bayangkan sebuah kotak yang digeser ke kanan atau ke atas, itu adalah contoh translasi.
- Refleksi: Pencerminan suatu bangun geometri terhadap garis tertentu. Bayangkan sebuah gambar yang dibalik, itu adalah contoh refleksi.
- Dilatasi: Perbesaran atau pengecilan suatu bangun geometri dengan faktor skala tertentu. Bayangkan sebuah lingkaran yang diperbesar atau diperkecil, itu adalah contoh dilatasi.
Contoh Ilustrasi Transformasi Geometri
| Jenis Transformasi | Ilustrasi | Keterangan |
|---|---|---|
| Rotasi | Bayangkan sebuah segitiga yang diputar 90 derajat searah jarum jam terhadap titik pusat (0,0). Posisi segitiga berubah, tetapi bentuk dan ukurannya tetap sama. | Sudut putar 90 derajat, arah putar searah jarum jam. |
| Translasi | Bayangkan sebuah persegi yang digeser 3 satuan ke kanan dan 2 satuan ke atas. Posisi persegi berubah, tetapi bentuk dan ukurannya tetap sama. | Pergeseran 3 satuan ke kanan dan 2 satuan ke atas. |
| Refleksi | Bayangkan sebuah lingkaran yang dicerminkan terhadap sumbu Y. Posisi lingkaran berubah, tetapi bentuk dan ukurannya tetap sama. | Pencerminan terhadap sumbu Y. |
| Dilatasi | Bayangkan sebuah persegi panjang yang diperbesar dengan faktor skala 2. Posisi persegi panjang berubah, bentuknya tetap sama, tetapi ukurannya menjadi dua kali lipat. | Faktor skala 2. |
Terakhir
Memahami konsep rotasi terhadap titik pusat (0,0) membuka pintu bagi kita untuk menjelajahi dunia geometri dengan lebih dalam. Mempelajari rumus, sifat-sifat, dan penerapannya dalam berbagai bidang akan memberikan pemahaman yang lebih komprehensif tentang transformasi geometri. Melalui contoh soal yang menarik dan ilustrasi yang jelas, kita dapat menjelajahi keindahan dan kompleksitas rotasi dalam geometri.






