Contoh soal segi empat dan segitiga – Segi empat dan segitiga merupakan bentuk geometri dasar yang sering kita temui dalam kehidupan sehari-hari. Dari bentuk rumah, meja, hingga potongan pizza, semuanya melibatkan konsep segi empat dan segitiga. Memahami konsep ini tidak hanya penting untuk pelajaran matematika, tetapi juga untuk memahami dunia di sekitar kita.
Dalam artikel ini, kita akan menjelajahi berbagai jenis segi empat dan segitiga, sifat-sifatnya, dan rumus untuk menghitung luas dan kelilingnya. Selain itu, kita juga akan melihat contoh soal dan penerapannya dalam berbagai bidang, seperti arsitektur, desain, dan teknik. Yuk, kita pelajari bersama!
Pengertian Segi Empat dan Segitiga
Segi empat dan segitiga merupakan dua bentuk geometri dasar yang sering kita jumpai dalam kehidupan sehari-hari. Kedua bentuk ini memiliki ciri khas yang berbeda, namun keduanya sama-sama penting dalam berbagai bidang, mulai dari arsitektur hingga ilmu pengetahuan.
Definisi Segi Empat dan Segitiga
Segi empat adalah bangun datar tertutup yang memiliki empat sisi dan empat sudut. Sedangkan segitiga adalah bangun datar tertutup yang memiliki tiga sisi dan tiga sudut.
Contoh Segi Empat dan Segitiga dalam Kehidupan Sehari-hari
Segi empat dan segitiga mudah kita temukan di sekitar kita. Berikut beberapa contohnya:
- Segi empat: Pintu, jendela, meja, buku, dan papan catur.
- Segitiga: Sepeda, potongan pizza, atap rumah, dan tanda peringatan.
Perbandingan Ciri-ciri Segi Empat dan Segitiga
Berikut tabel perbandingan ciri-ciri segi empat dan segitiga:
| Ciri | Segi Empat | Segitiga |
|---|---|---|
| Jumlah Sisi | 4 | 3 |
| Jumlah Sudut | 4 | 3 |
| Sifat Khusus |
|
|
Jenis-Jenis Segi Empat
Segi empat merupakan bangun datar yang memiliki empat sisi dan empat sudut. Jenis-jenis segi empat dibedakan berdasarkan ciri-ciri khusus yang dimilikinya, seperti panjang sisi, besar sudut, dan sifat paralel pada sisinya.
Persegi
Persegi adalah segi empat yang memiliki keempat sisinya sama panjang dan keempat sudutnya siku-siku (90 derajat).
- Ciri-ciri persegi:
- Keempat sisinya sama panjang.
- Keempat sudutnya siku-siku (90 derajat).
- Diagonalnya sama panjang dan saling tegak lurus.
- Diagonalnya membagi persegi menjadi empat segitiga siku-siku kongruen.
- Contoh Soal:
Sebuah persegi memiliki panjang sisi 5 cm. Hitunglah luas dan keliling persegi tersebut!
Penyelesaian:
- Luas persegi = sisi x sisi = 5 cm x 5 cm = 25 cm2
- Keliling persegi = 4 x sisi = 4 x 5 cm = 20 cm
Persegi Panjang
Persegi panjang adalah segi empat yang memiliki dua pasang sisi yang sejajar dan sama panjang, serta keempat sudutnya siku-siku (90 derajat).
- Ciri-ciri persegi panjang:
- Dua pasang sisi yang sejajar dan sama panjang.
- Keempat sudutnya siku-siku (90 derajat).
- Diagonalnya sama panjang.
- Diagonalnya membagi persegi panjang menjadi dua segitiga siku-siku kongruen.
- Contoh Soal:
Sebuah persegi panjang memiliki panjang 8 cm dan lebar 5 cm. Hitunglah luas dan keliling persegi panjang tersebut!
Penyelesaian:
- Luas persegi panjang = panjang x lebar = 8 cm x 5 cm = 40 cm2
- Keliling persegi panjang = 2 x (panjang + lebar) = 2 x (8 cm + 5 cm) = 26 cm
Jajar Genjang
Jajar genjang adalah segi empat yang memiliki dua pasang sisi yang sejajar dan sama panjang, tetapi keempat sudutnya tidak selalu siku-siku.
- Ciri-ciri jajar genjang:
- Dua pasang sisi yang sejajar dan sama panjang.
- Sudut yang berhadapan sama besar.
- Diagonalnya saling membagi dua.
- Contoh Soal:
Sebuah jajar genjang memiliki alas 10 cm, tinggi 6 cm, dan salah satu sudutnya 60 derajat. Hitunglah luas jajar genjang tersebut!
Penyelesaian:
- Luas jajar genjang = alas x tinggi = 10 cm x 6 cm = 60 cm2
Trapesium
Trapesium adalah segi empat yang memiliki tepat satu pasang sisi yang sejajar.
- Ciri-ciri trapesium:
- Memiliki tepat satu pasang sisi yang sejajar.
- Jumlah sudut-sudut yang berdekatan pada sisi sejajar adalah 180 derajat.
- Contoh Soal:
Sebuah trapesium memiliki panjang sisi sejajar 8 cm dan 12 cm, serta tinggi 5 cm. Hitunglah luas trapesium tersebut!
Penyelesaian:
- Luas trapesium = 1/2 x (jumlah sisi sejajar) x tinggi = 1/2 x (8 cm + 12 cm) x 5 cm = 50 cm2
Layang-layang
Layang-layang adalah segi empat yang memiliki dua pasang sisi yang berdekatan sama panjang.
- Ciri-ciri layang-layang:
- Dua pasang sisi yang berdekatan sama panjang.
- Diagonalnya saling tegak lurus.
- Salah satu diagonalnya membagi layang-layang menjadi dua segitiga sama kaki yang kongruen.
- Contoh Soal:
Sebuah layang-layang memiliki panjang diagonal 10 cm dan 8 cm. Hitunglah luas layang-layang tersebut!
Penyelesaian:
- Luas layang-layang = 1/2 x (diagonal 1 x diagonal 2) = 1/2 x (10 cm x 8 cm) = 40 cm2
Tabel Ringkasan Jenis Segi Empat
| Jenis Segi Empat | Ciri-ciri | Contoh Soal |
|---|---|---|
| Persegi | Keempat sisinya sama panjang, keempat sudutnya siku-siku | Hitung luas dan keliling persegi dengan sisi 5 cm. |
| Persegi Panjang | Dua pasang sisi yang sejajar dan sama panjang, keempat sudutnya siku-siku | Hitung luas dan keliling persegi panjang dengan panjang 8 cm dan lebar 5 cm. |
| Jajar Genjang | Dua pasang sisi yang sejajar dan sama panjang, sudut yang berhadapan sama besar | Hitung luas jajar genjang dengan alas 10 cm, tinggi 6 cm, dan sudut 60 derajat. |
| Trapesium | Memiliki tepat satu pasang sisi yang sejajar | Hitung luas trapesium dengan sisi sejajar 8 cm dan 12 cm, serta tinggi 5 cm. |
| Layang-layang | Dua pasang sisi yang berdekatan sama panjang, diagonalnya saling tegak lurus | Hitung luas layang-layang dengan diagonal 10 cm dan 8 cm. |
Jenis-Jenis Segitiga
Segitiga merupakan bangun datar yang memiliki tiga sisi dan tiga sudut. Segitiga dapat diklasifikasikan berdasarkan panjang sisi dan besar sudutnya. Klasifikasi ini membantu kita memahami sifat-sifat dan karakteristik setiap jenis segitiga.
Berdasarkan Panjang Sisi
Berdasarkan panjang sisinya, segitiga dapat dibedakan menjadi tiga jenis:
- Segitiga Sama Sisi: Segitiga yang memiliki ketiga sisinya sama panjang. Ketiga sudutnya juga sama besar, yaitu 60 derajat.
- Segitiga Sama Kaki: Segitiga yang memiliki dua sisi yang sama panjang. Kedua sudut yang berhadapan dengan sisi yang sama panjang juga sama besar.
- Segitiga Sembarang: Segitiga yang memiliki ketiga sisinya berbeda panjang. Ketiga sudutnya juga berbeda besar.
Berdasarkan Besar Sudut
Berdasarkan besar sudutnya, segitiga dapat dibedakan menjadi tiga jenis:
- Segitiga Siku-Siku: Segitiga yang memiliki satu sudut siku-siku (90 derajat). Sisi yang berhadapan dengan sudut siku-siku disebut hipotenusa, sedangkan dua sisi lainnya disebut kaki.
- Segitiga Lancip: Segitiga yang memiliki ketiga sudutnya lancip (kurang dari 90 derajat).
- Segitiga Tumpul: Segitiga yang memiliki satu sudut tumpul (lebih dari 90 derajat).
Contoh Soal dan Cara Menentukan Jenis Segitiga
Berikut adalah contoh soal dan cara menentukan jenis segitiga berdasarkan informasi yang diberikan:
| Jenis Segitiga | Ciri-Ciri | Contoh Soal |
|---|---|---|
| Segitiga Sama Sisi | Ketiga sisinya sama panjang. Ketiga sudutnya sama besar (60 derajat). | Sebuah segitiga memiliki panjang sisi 5 cm, 5 cm, dan 5 cm. Tentukan jenis segitiga tersebut. |
| Segitiga Sama Kaki | Dua sisi yang sama panjang. Dua sudut yang berhadapan dengan sisi yang sama panjang juga sama besar. | Sebuah segitiga memiliki panjang sisi 4 cm, 4 cm, dan 6 cm. Tentukan jenis segitiga tersebut. |
| Segitiga Sembarang | Ketiga sisinya berbeda panjang. Ketiga sudutnya juga berbeda besar. | Sebuah segitiga memiliki panjang sisi 3 cm, 4 cm, dan 5 cm. Tentukan jenis segitiga tersebut. |
| Segitiga Siku-Siku | Memiliki satu sudut siku-siku (90 derajat). | Sebuah segitiga memiliki sudut 90 derajat, 45 derajat, dan 45 derajat. Tentukan jenis segitiga tersebut. |
| Segitiga Lancip | Ketiga sudutnya lancip (kurang dari 90 derajat). | Sebuah segitiga memiliki sudut 60 derajat, 70 derajat, dan 50 derajat. Tentukan jenis segitiga tersebut. |
| Segitiga Tumpul | Memiliki satu sudut tumpul (lebih dari 90 derajat). | Sebuah segitiga memiliki sudut 110 derajat, 40 derajat, dan 30 derajat. Tentukan jenis segitiga tersebut. |
Untuk menentukan jenis segitiga, kita dapat menggunakan informasi tentang panjang sisi dan besar sudut. Jika ketiga sisi sama panjang, maka segitiga tersebut adalah segitiga sama sisi. Jika dua sisi sama panjang, maka segitiga tersebut adalah segitiga sama kaki. Jika ketiga sisi berbeda panjang, maka segitiga tersebut adalah segitiga sembarang. Jika segitiga memiliki satu sudut siku-siku, maka segitiga tersebut adalah segitiga siku-siku. Jika ketiga sudutnya lancip, maka segitiga tersebut adalah segitiga lancip. Jika segitiga memiliki satu sudut tumpul, maka segitiga tersebut adalah segitiga tumpul.
Rumus Luas dan Keliling Segi Empat: Contoh Soal Segi Empat Dan Segitiga
Segi empat merupakan bangun datar yang memiliki empat sisi dan empat sudut. Ada berbagai jenis segi empat, seperti persegi, persegi panjang, jajar genjang, belah ketupat, trapesium, dan layang-layang. Setiap jenis segi empat memiliki rumus luas dan keliling yang berbeda. Untuk menghitung luas dan keliling segi empat, kita perlu mengetahui panjang sisi-sisinya.
Rumus Luas dan Keliling Segi Empat
Berikut adalah rumus luas dan keliling untuk setiap jenis segi empat:
- Persegi
- Luas: sisi x sisi
- Keliling: 4 x sisi
- Persegi Panjang
- Luas: panjang x lebar
- Keliling: 2 x (panjang + lebar)
- Jajar Genjang
- Luas: alas x tinggi
- Keliling: 2 x (alas + sisi miring)
- Belah Ketupat
- Luas: 1/2 x diagonal 1 x diagonal 2
- Keliling: 4 x sisi
- Trapesium
- Luas: 1/2 x (alas 1 + alas 2) x tinggi
- Keliling: sisi 1 + sisi 2 + sisi 3 + sisi 4
- Layang-layang
- Luas: 1/2 x diagonal 1 x diagonal 2
- Keliling: sisi 1 + sisi 2 + sisi 3 + sisi 4
Contoh Soal dan Penyelesaian
Berikut adalah contoh soal dan langkah-langkah penyelesaian untuk menghitung luas dan keliling segi empat:
Persegi
Sebuah persegi memiliki sisi sepanjang 5 cm. Hitunglah luas dan keliling persegi tersebut!
Penyelesaian:
- Luas: sisi x sisi = 5 cm x 5 cm = 25 cm2
- Keliling: 4 x sisi = 4 x 5 cm = 20 cm
Persegi Panjang
Sebuah persegi panjang memiliki panjang 10 cm dan lebar 5 cm. Hitunglah luas dan keliling persegi panjang tersebut!
Penyelesaian:
- Luas: panjang x lebar = 10 cm x 5 cm = 50 cm2
- Keliling: 2 x (panjang + lebar) = 2 x (10 cm + 5 cm) = 30 cm
Jajar Genjang
Sebuah jajar genjang memiliki alas 8 cm, tinggi 5 cm, dan sisi miring 6 cm. Hitunglah luas dan keliling jajar genjang tersebut!
Penyelesaian:
- Luas: alas x tinggi = 8 cm x 5 cm = 40 cm2
- Keliling: 2 x (alas + sisi miring) = 2 x (8 cm + 6 cm) = 28 cm
Belah Ketupat
Sebuah belah ketupat memiliki diagonal 1 sepanjang 12 cm dan diagonal 2 sepanjang 16 cm. Hitunglah luas dan keliling belah ketupat tersebut!
Penyelesaian:
- Luas: 1/2 x diagonal 1 x diagonal 2 = 1/2 x 12 cm x 16 cm = 96 cm2
- Keliling: 4 x sisi = 4 x 10 cm = 40 cm (sisi belah ketupat dapat dihitung dengan teorema Pythagoras)
Trapesium
Sebuah trapesium memiliki alas 1 10 cm, alas 2 6 cm, tinggi 4 cm, dan sisi miring 5 cm dan 7 cm. Hitunglah luas dan keliling trapesium tersebut!
Penyelesaian:
- Luas: 1/2 x (alas 1 + alas 2) x tinggi = 1/2 x (10 cm + 6 cm) x 4 cm = 32 cm2
- Keliling: sisi 1 + sisi 2 + sisi 3 + sisi 4 = 10 cm + 6 cm + 5 cm + 7 cm = 28 cm
Layang-layang
Sebuah layang-layang memiliki diagonal 1 sepanjang 10 cm dan diagonal 2 sepanjang 8 cm. Hitunglah luas dan keliling layang-layang tersebut!
Penyelesaian:
- Luas: 1/2 x diagonal 1 x diagonal 2 = 1/2 x 10 cm x 8 cm = 40 cm2
- Keliling: sisi 1 + sisi 2 + sisi 3 + sisi 4 = 6 cm + 6 cm + 5 cm + 5 cm = 22 cm (sisi layang-layang dapat dihitung dengan teorema Pythagoras)
Tabel Rumus Luas dan Keliling Segi Empat
| Jenis Segi Empat | Rumus Luas | Rumus Keliling |
|---|---|---|
| Persegi | sisi x sisi | 4 x sisi |
| Persegi Panjang | panjang x lebar | 2 x (panjang + lebar) |
| Jajar Genjang | alas x tinggi | 2 x (alas + sisi miring) |
| Belah Ketupat | 1/2 x diagonal 1 x diagonal 2 | 4 x sisi |
| Trapesium | 1/2 x (alas 1 + alas 2) x tinggi | sisi 1 + sisi 2 + sisi 3 + sisi 4 |
| Layang-layang | 1/2 x diagonal 1 x diagonal 2 | sisi 1 + sisi 2 + sisi 3 + sisi 4 |
Rumus Luas dan Keliling Segitiga
Segitiga adalah bangun datar yang memiliki tiga sisi dan tiga sudut. Jenis-jenis segitiga dibedakan berdasarkan panjang sisi dan besar sudutnya. Rumus luas dan keliling segitiga dapat digunakan untuk menghitung luas dan keliling dari berbagai jenis segitiga.
Rumus Luas Segitiga
Luas segitiga adalah ukuran area yang dibatasi oleh ketiga sisinya. Rumus luas segitiga adalah:
Luas = 1/2 x alas x tinggi
Keterangan:
- Alas adalah salah satu sisi segitiga.
- Tinggi adalah garis tegak lurus dari titik sudut yang berhadapan dengan alas ke alas segitiga.
Rumus Keliling Segitiga
Keliling segitiga adalah jumlah panjang ketiga sisinya. Rumus keliling segitiga adalah:
Keliling = sisi 1 + sisi 2 + sisi 3
Contoh Soal Luas dan Keliling Segitiga
Berikut adalah contoh soal dan langkah-langkah penyelesaian untuk menghitung luas dan keliling segitiga:
Contoh Soal Luas Segitiga
Sebuah segitiga memiliki alas 10 cm dan tinggi 8 cm. Hitunglah luas segitiga tersebut!
Penyelesaian:
- Diketahui: alas = 10 cm, tinggi = 8 cm.
- Rumus luas segitiga: Luas = 1/2 x alas x tinggi.
- Substitusikan nilai alas dan tinggi ke dalam rumus: Luas = 1/2 x 10 cm x 8 cm = 40 cm2.
- Jadi, luas segitiga tersebut adalah 40 cm2.
Contoh Soal Keliling Segitiga
Sebuah segitiga memiliki sisi-sisi dengan panjang 5 cm, 7 cm, dan 9 cm. Hitunglah keliling segitiga tersebut!
Penyelesaian:
- Diketahui: sisi 1 = 5 cm, sisi 2 = 7 cm, sisi 3 = 9 cm.
- Rumus keliling segitiga: Keliling = sisi 1 + sisi 2 + sisi 3.
- Substitusikan nilai sisi-sisi ke dalam rumus: Keliling = 5 cm + 7 cm + 9 cm = 21 cm.
- Jadi, keliling segitiga tersebut adalah 21 cm.
Tabel Rumus Luas dan Keliling Segitiga
| Jenis Segitiga | Rumus Luas | Rumus Keliling |
|---|---|---|
| Segitiga Siku-siku | Luas = 1/2 x alas x tinggi | Keliling = sisi 1 + sisi 2 + sisi 3 |
| Segitiga Sama Kaki | Luas = 1/2 x alas x tinggi | Keliling = 2 x sisi sama kaki + alas |
| Segitiga Sama Sisi | Luas = √3/4 x sisi2 | Keliling = 3 x sisi |
Sifat-Sifat Khusus Segi Empat
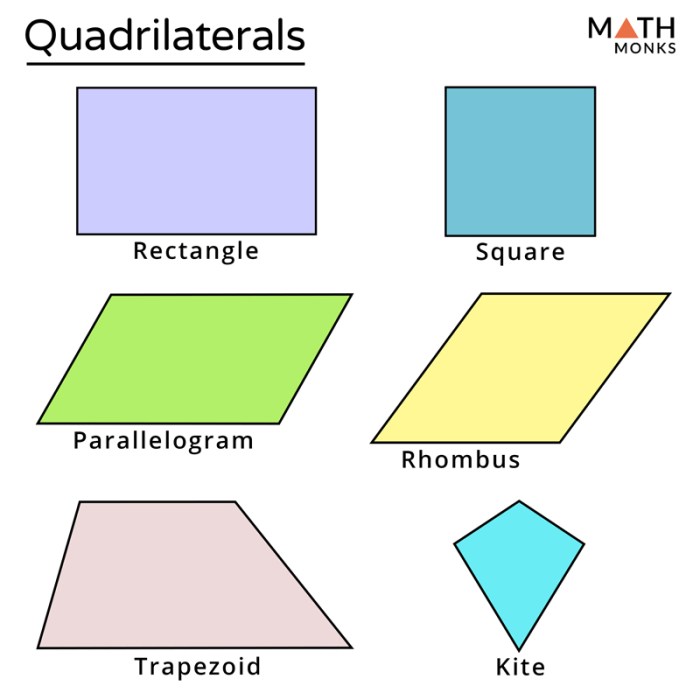
Segi empat adalah bangun datar yang memiliki empat sisi dan empat sudut. Ada berbagai jenis segi empat, masing-masing dengan sifat-sifat khusus yang membedakannya. Sifat-sifat khusus ini sangat penting dalam menyelesaikan berbagai masalah geometri, seperti menghitung luas, keliling, dan sudut-sudutnya.
Sifat-Sifat Khusus Segi Empat
Berikut ini adalah beberapa sifat khusus yang dimiliki oleh setiap jenis segi empat:
- Persegi Panjang : Memiliki empat sudut siku-siku, sisi-sisi yang berhadapan sejajar dan sama panjang, dan diagonal yang sama panjang dan saling membagi dua.
- Persegi : Memiliki empat sudut siku-siku, semua sisi sama panjang, dan diagonal yang sama panjang, saling membagi dua, dan saling tegak lurus.
- Jajar Genjang : Memiliki sisi-sisi yang berhadapan sejajar dan sama panjang, sudut-sudut yang berhadapan sama besar, dan diagonal yang saling membagi dua.
- Belah Ketupat : Memiliki semua sisi sama panjang, sudut-sudut yang berhadapan sama besar, diagonal yang saling membagi dua dan saling tegak lurus.
- Trapesium : Memiliki satu pasang sisi sejajar, yang disebut alas dan tinggi. Dua sisi lainnya tidak sejajar. Diagonal trapesium saling membagi dua.
- Trapesium Siku-Siku : Memiliki satu sudut siku-siku.
- Trapesium Sama Kaki : Memiliki dua sisi miring yang sama panjang dan dua sudut alas yang sama besar.
Contoh Soal dan Penyelesaian
Berikut ini adalah contoh soal dan penyelesaian yang memanfaatkan sifat-sifat khusus segi empat:
Soal:
Sebuah persegi panjang memiliki panjang 12 cm dan lebar 8 cm. Tentukan panjang diagonalnya!
Mencari contoh soal segi empat dan segitiga? Kamu bisa menemukan banyak soal latihan di buku teks atau website edukasi. Nah, kalau kamu tertarik untuk mempelajari materi yang lebih menantang, coba deh cek contoh soal grafik fungsi eksponen dan jawabannya.
Setelah itu, kamu bisa kembali berlatih soal segi empat dan segitiga dengan pemahaman yang lebih luas tentang konsep matematika.
Penyelesaian:
Diagonal persegi panjang membagi persegi panjang menjadi dua segitiga siku-siku. Dengan menggunakan teorema Pythagoras, kita dapat menghitung panjang diagonalnya:
Diagonal2 = Panjang2 + Lebar2
Diagonal2 = 122 + 82
Diagonal2 = 144 + 64
Diagonal2 = 208
Diagonal = √208 = 4√13 cm
Jadi, panjang diagonal persegi panjang tersebut adalah 4√13 cm.
Tabel Sifat-Sifat Khusus Segi Empat
| Jenis Segi Empat | Jumlah Sudut | Simetri | Diagonal |
|---|---|---|---|
| Persegi Panjang | 4 sudut siku-siku | 2 sumbu simetri | Sama panjang, saling membagi dua |
| Persegi | 4 sudut siku-siku | 4 sumbu simetri | Sama panjang, saling membagi dua, saling tegak lurus |
| Jajar Genjang | Sudut-sudut yang berhadapan sama besar | Tidak memiliki sumbu simetri | Saling membagi dua |
| Belah Ketupat | Sudut-sudut yang berhadapan sama besar | 2 sumbu simetri | Saling membagi dua, saling tegak lurus |
| Trapesium | Tidak memiliki sifat khusus | Tidak memiliki sumbu simetri | Tidak memiliki sifat khusus |
| Trapesium Siku-Siku | Memiliki satu sudut siku-siku | Tidak memiliki sumbu simetri | Tidak memiliki sifat khusus |
| Trapesium Sama Kaki | Dua sudut alas sama besar | 1 sumbu simetri | Tidak memiliki sifat khusus |
Sifat-Sifat Khusus Segitiga
Segitiga, sebagai bangun datar yang memiliki tiga sisi dan tiga sudut, memiliki sifat-sifat khusus yang membedakannya dari bangun datar lainnya. Sifat-sifat ini sangat penting dalam mempelajari geometri dan membantu kita memahami berbagai hubungan antar sisi dan sudut segitiga. Dalam pembahasan ini, kita akan menjelajahi beberapa sifat khusus yang dimiliki oleh segitiga, termasuk teorema Pythagoras, garis tinggi, dan jumlah sudut.
Jenis-Jenis Segitiga dan Sifat-Sifatnya
Berdasarkan panjang sisinya, segitiga dapat dibedakan menjadi tiga jenis:
- Segitiga Sama Sisi: Ketiga sisinya memiliki panjang yang sama. Setiap sudutnya berukuran 60 derajat.
- Segitiga Sama Kaki: Dua sisinya memiliki panjang yang sama. Dua sudut yang berhadapan dengan sisi yang sama panjang juga memiliki ukuran yang sama.
- Segitiga Sembarang: Ketiga sisinya memiliki panjang yang berbeda. Ukuran sudutnya juga berbeda.
Berdasarkan besar sudutnya, segitiga dapat dibedakan menjadi tiga jenis:
- Segitiga Siku-Siku: Salah satu sudutnya berukuran 90 derajat. Sisi yang berhadapan dengan sudut siku-siku disebut hipotenusa, sedangkan dua sisi lainnya disebut kaki.
- Segitiga Lancip: Ketiga sudutnya berukuran kurang dari 90 derajat.
- Segitiga Tumpul: Salah satu sudutnya berukuran lebih dari 90 derajat.
Teorema Pythagoras, Contoh soal segi empat dan segitiga
Teorema Pythagoras adalah salah satu sifat khusus yang berlaku untuk segitiga siku-siku. Teorema ini menyatakan bahwa kuadrat hipotenusa sama dengan jumlah kuadrat kedua kakinya.
a2 + b2 = c2
di mana:
- a dan b adalah panjang kaki segitiga siku-siku
- c adalah panjang hipotenusa
Teorema Pythagoras dapat digunakan untuk mencari panjang salah satu sisi segitiga siku-siku jika dua sisi lainnya diketahui.
Contoh Soal 1
Sebuah segitiga siku-siku memiliki panjang kaki 3 cm dan 4 cm. Tentukan panjang hipotenusanya!
Penyelesaian:
Dengan menggunakan teorema Pythagoras, kita dapat menghitung panjang hipotenusa (c):
c2 = a2 + b2
c2 = 32 + 42
c2 = 9 + 16
c2 = 25
c = √25
c = 5 cm
Jadi, panjang hipotenusa segitiga tersebut adalah 5 cm.
Garis Tinggi
Garis tinggi segitiga adalah garis tegak lurus yang ditarik dari suatu titik sudut ke sisi yang berhadapan (atau perpanjangannya). Garis tinggi membagi segitiga menjadi dua segitiga siku-siku. Panjang garis tinggi dapat dihitung dengan menggunakan rumus luas segitiga.
Contoh Soal 2
Sebuah segitiga memiliki alas 6 cm dan tinggi 4 cm. Tentukan luas segitiga tersebut!
Penyelesaian:
Luas segitiga dapat dihitung dengan rumus:
Luas = 1/2 x alas x tinggi
Dengan memasukkan nilai alas dan tinggi yang diketahui, kita dapat menghitung luas segitiga:
Luas = 1/2 x 6 cm x 4 cm
Luas = 12 cm2
Jadi, luas segitiga tersebut adalah 12 cm2.
Jumlah Sudut Segitiga
Jumlah sudut dalam setiap segitiga selalu sama, yaitu 180 derajat. Hal ini dapat dibuktikan dengan menarik garis sejajar dengan salah satu sisi segitiga.
Contoh Soal 3
Sebuah segitiga memiliki dua sudut yang berukuran 50 derajat dan 70 derajat. Tentukan besar sudut ketiga!
Penyelesaian:
Jumlah ketiga sudut dalam segitiga adalah 180 derajat. Oleh karena itu, besar sudut ketiga dapat dihitung dengan:
Sudut ketiga = 180 derajat – 50 derajat – 70 derajat
Sudut ketiga = 60 derajat
Jadi, besar sudut ketiga segitiga tersebut adalah 60 derajat.
Tabel Sifat-Sifat Khusus Segitiga
| Jenis Segitiga | Sifat Khusus |
|---|---|
| Segitiga Sama Sisi | Ketiga sisinya sama panjang. Setiap sudutnya berukuran 60 derajat. |
| Segitiga Sama Kaki | Dua sisinya sama panjang. Dua sudut yang berhadapan dengan sisi yang sama panjang juga memiliki ukuran yang sama. |
| Segitiga Sembarang | Ketiga sisinya memiliki panjang yang berbeda. Ukuran sudutnya juga berbeda. |
| Segitiga Siku-Siku | Salah satu sudutnya berukuran 90 derajat. Sisi yang berhadapan dengan sudut siku-siku disebut hipotenusa, sedangkan dua sisi lainnya disebut kaki. |
| Segitiga Lancip | Ketiga sudutnya berukuran kurang dari 90 derajat. |
| Segitiga Tumpul | Salah satu sudutnya berukuran lebih dari 90 derajat. |
Penerapan Segi Empat dan Segitiga dalam Kehidupan Sehari-hari
Segi empat dan segitiga merupakan bentuk geometri dasar yang sering kita jumpai dalam kehidupan sehari-hari. Bentuk-bentuk ini tidak hanya hadir dalam buku pelajaran matematika, tetapi juga diterapkan dalam berbagai bidang, mulai dari arsitektur hingga teknik. Sifat-sifat geometri yang melekat pada segi empat dan segitiga menjadi kunci dalam menentukan stabilitas, kekuatan, dan keindahan desain dalam berbagai aplikasi.
Arsitektur
Dalam arsitektur, segi empat dan segitiga menjadi elemen dasar dalam membangun struktur yang kokoh dan estetis. Bangunan dengan bentuk segi empat, seperti rumah, gedung perkantoran, dan hotel, menawarkan ruang yang luas dan fleksibel. Sifat-sifat segi empat, seperti kestabilan dan kekuatan, menjadikan bentuk ini ideal untuk membangun dinding, lantai, dan atap yang kuat. Segitiga, di sisi lain, memiliki sifat-sifat yang unik yang membuatnya ideal untuk membangun struktur yang kuat dan tahan terhadap beban berat. Misalnya, bentuk segitiga digunakan dalam konstruksi rangka atap, jembatan, dan menara, karena sifatnya yang kuat dan stabil.
Desain
Dalam desain, segi empat dan segitiga menjadi elemen visual yang kuat dalam menciptakan komposisi yang menarik dan harmonis. Dalam desain grafis, segi empat dan segitiga sering digunakan sebagai bentuk dasar untuk membuat logo, poster, dan ilustrasi. Sifat-sifat geometri dari segi empat dan segitiga, seperti simetri, keseimbangan, dan proporsi, memainkan peran penting dalam menciptakan desain yang estetis dan mudah dipahami. Contohnya, logo perusahaan sering kali menggunakan bentuk segi empat atau segitiga untuk memberikan kesan yang kuat, sederhana, dan mudah diingat.
Teknik
Dalam teknik, segi empat dan segitiga memainkan peran penting dalam berbagai aplikasi, mulai dari desain mesin hingga konstruksi jembatan. Bentuk segi empat, dengan sifat-sifatnya yang stabil dan mudah dihitung, sering digunakan dalam desain mesin dan struktur. Misalnya, dalam desain mesin, segi empat digunakan untuk membangun blok mesin, rangka, dan komponen lainnya. Segitiga, dengan sifatnya yang kuat dan tahan terhadap beban, sering digunakan dalam konstruksi jembatan, rangka atap, dan menara. Dalam konstruksi jembatan, segitiga digunakan untuk membentuk rangka jembatan yang kuat dan stabil, sehingga mampu menahan beban berat dan tekanan dari lalu lintas.
Tabel Penerapan Segi Empat dan Segitiga
| Penerapan | Bidang | Sifat Geometri yang Berperan |
|---|---|---|
| Bangunan Rumah | Arsitektur | Kestabilan, kekuatan |
| Rangka Atap | Arsitektur | Kekuatan, stabilitas |
| Logo Perusahaan | Desain | Simetri, keseimbangan |
| Blok Mesin | Teknik | Kestabilan, kekuatan |
| Rangka Jembatan | Teknik | Kekuatan, stabilitas |
Soal-Soal Latihan Segi Empat dan Segitiga
Segi empat dan segitiga merupakan bentuk geometri dasar yang sering dijumpai dalam kehidupan sehari-hari. Untuk memahami konsep kedua bentuk geometri ini dengan lebih baik, berikut disajikan beberapa soal latihan yang dapat dicoba.
Soal Latihan dan Kunci Jawaban
Berikut adalah 5 soal latihan yang menguji pemahaman tentang konsep segi empat dan segitiga, beserta kunci jawabannya.
| No. | Soal | Kunci Jawaban |
|---|---|---|
| 1. | Sebuah persegi panjang memiliki panjang 10 cm dan lebar 5 cm. Berapakah keliling persegi panjang tersebut? | Keliling = 2 x (panjang + lebar) = 2 x (10 cm + 5 cm) = 30 cm |
| 2. | Sebuah segitiga siku-siku memiliki panjang sisi miring 13 cm dan salah satu sisi tegaknya 5 cm. Berapakah panjang sisi tegak lainnya? | Dengan teorema Pythagoras, panjang sisi tegak lainnya adalah √(13² – 5²) = √(169 – 25) = √144 = 12 cm |
| 3. | Sebuah belah ketupat memiliki panjang diagonal 12 cm dan 16 cm. Berapakah luas belah ketupat tersebut? | Luas belah ketupat = ½ x (diagonal 1 x diagonal 2) = ½ x (12 cm x 16 cm) = 96 cm² |
| 4. | Sebuah trapesium memiliki panjang sisi sejajar 8 cm dan 12 cm, serta tinggi 5 cm. Berapakah luas trapesium tersebut? | Luas trapesium = ½ x (sisi sejajar 1 + sisi sejajar 2) x tinggi = ½ x (8 cm + 12 cm) x 5 cm = 50 cm² |
| 5. | Sebuah segitiga sama sisi memiliki panjang sisi 6 cm. Berapakah luas segitiga tersebut? | Luas segitiga sama sisi = (√3/4) x sisi² = (√3/4) x 6² cm² = 9√3 cm² |
Tips dan Trik Mengerjakan Soal Segi Empat dan Segitiga
Materi geometri, khususnya tentang segi empat dan segitiga, sering muncul dalam berbagai ujian, mulai dari ujian sekolah hingga ujian masuk perguruan tinggi. Untuk menguasai materi ini dan menyelesaikan soal-soal dengan tepat, kamu perlu memahami konsep dasar dan menerapkan beberapa tips dan trik yang efektif. Berikut adalah beberapa tips dan trik yang bisa kamu gunakan untuk meningkatkan kemampuanmu dalam mengerjakan soal-soal segi empat dan segitiga.
Memahami Konsep Dasar
Langkah pertama yang penting adalah memahami konsep dasar dari segi empat dan segitiga. Tanpa pemahaman yang kuat tentang konsep dasar, kamu akan kesulitan dalam menyelesaikan soal-soal yang lebih kompleks.
- Definisi dan Sifat: Pastikan kamu memahami definisi dan sifat-sifat dari setiap jenis segi empat dan segitiga, seperti persegi panjang, persegi, jajar genjang, trapesium, segitiga siku-siku, segitiga sama kaki, dan segitiga sama sisi.
- Rumus Luas dan Keliling: Pelajari dan hafalkan rumus luas dan keliling dari setiap jenis segi empat dan segitiga. Kemampuan untuk mengingat rumus ini akan mempercepat proses perhitungan.
- Teorema Pythagoras: Teorema Pythagoras sangat penting untuk menyelesaikan soal-soal yang melibatkan segitiga siku-siku. Pastikan kamu memahami teorema ini dan bisa menerapkannya dalam berbagai situasi.
Mengenali Pola dan Hubungan
Banyak soal segi empat dan segitiga melibatkan pola dan hubungan antar bangun geometri. Kemampuan untuk mengenali pola ini akan sangat membantu dalam menyelesaikan soal.
- Hubungan Sudut: Perhatikan hubungan antar sudut dalam segi empat dan segitiga. Misalnya, jumlah sudut dalam segitiga selalu 180 derajat, sedangkan jumlah sudut dalam segi empat selalu 360 derajat.
- Hubungan Sisi: Pelajari hubungan antar sisi dalam segi empat dan segitiga. Misalnya, sisi-sisi yang berhadapan pada jajar genjang memiliki panjang yang sama, dan sisi-sisi yang berhadapan pada persegi panjang memiliki panjang yang sama.
- Kesamaan dan Kongruensi: Pahami konsep kesamaan dan kongruensi dalam segi empat dan segitiga. Dua bangun dikatakan sama jika memiliki bentuk yang sama, sedangkan dua bangun dikatakan kongruen jika memiliki bentuk dan ukuran yang sama.
Strategi Menyelesaikan Soal
Berikut adalah beberapa strategi yang dapat kamu gunakan untuk menyelesaikan soal-soal segi empat dan segitiga:
- Membuat Gambar: Selalu buat gambar untuk membantu memvisualisasikan soal. Gambar yang jelas akan memudahkanmu dalam memahami hubungan antar bangun geometri.
- Menuliskan Rumus: Sebelum menyelesaikan soal, tuliskan rumus yang relevan dengan soal tersebut. Hal ini akan membantu kamu dalam mengingat rumus dan menghindari kesalahan.
- Mencari Hubungan: Perhatikan hubungan antar bangun geometri dalam soal. Misalnya, jika terdapat segitiga siku-siku, kamu bisa menggunakan teorema Pythagoras.
- Menghindari Kesalahan Umum: Perhatikan kesalahan umum yang sering terjadi dalam mengerjakan soal segi empat dan segitiga, seperti salah menggunakan rumus atau salah menafsirkan gambar.
Melatih Kemampuan
Latihan adalah kunci untuk menguasai materi geometri. Semakin banyak kamu berlatih, semakin mahir kamu dalam menyelesaikan soal-soal.
- Kerjakan Soal Latihan: Cari soal latihan yang banyak dan beragam. Soal latihan akan membantu kamu dalam mengasah kemampuan dan mengidentifikasi kelemahan.
- Berdiskusi dengan Teman: Berdiskusi dengan teman tentang soal-soal yang sulit. Diskusi akan membantu kamu dalam memahami konsep dan menemukan solusi yang tepat.
- Mencari Referensi: Cari referensi tambahan, seperti buku, website, atau video, untuk mempelajari materi geometri dengan lebih mendalam.
Contoh Soal dan Pembahasan
Untuk lebih memahami tips dan trik yang telah dibahas, berikut adalah contoh soal dan pembahasannya.
| No | Soal | Pembahasan |
|---|---|---|
| 1 | Sebuah persegi panjang memiliki panjang 12 cm dan lebar 8 cm. Hitunglah luas persegi panjang tersebut! | Luas persegi panjang = panjang x lebar = 12 cm x 8 cm = 96 cm2 |
| 2 | Sebuah segitiga siku-siku memiliki panjang sisi siku-sikunya 5 cm dan 12 cm. Hitunglah panjang sisi miringnya! | Berdasarkan teorema Pythagoras, panjang sisi miring = √(52 + 122) = √(25 + 144) = √169 = 13 cm |
Terakhir
Dengan memahami konsep segi empat dan segitiga, kita dapat menyelesaikan berbagai masalah geometri dengan lebih mudah. Penerapannya dalam berbagai bidang menunjukkan betapa pentingnya mempelajari bentuk-bentuk dasar ini. Semoga artikel ini bermanfaat untuk meningkatkan pemahaman Anda tentang segi empat dan segitiga.






