Contoh soal sinus – Sinus, salah satu fungsi trigonometri dasar, memegang peran penting dalam berbagai bidang seperti fisika, teknik, dan seni. Konsep sinus membantu kita memahami hubungan antara sudut dan sisi dalam segitiga siku-siku, yang memiliki aplikasi luas dalam kehidupan sehari-hari. Dari menghitung tinggi bangunan hingga menganalisis gelombang suara, sinus hadir sebagai alat yang ampuh dalam menyelesaikan berbagai masalah. Mari kita telusuri lebih dalam tentang sinus melalui contoh soal yang menarik dan mudah dipahami.
Artikel ini akan membahas konsep sinus secara mendalam, mulai dari definisi hingga penerapannya dalam berbagai situasi. Kita akan mempelajari rumus sinus, menggambar grafik fungsi sinus, dan menjelajahi hubungannya dengan fungsi trigonometri lainnya. Selain itu, Anda akan menemukan berbagai contoh soal latihan yang dirancang untuk membantu Anda memahami dan menguasai konsep sinus dengan lebih baik.
Pengertian Sinus: Contoh Soal Sinus
Sinus dalam matematika merupakan salah satu fungsi trigonometri yang memiliki peranan penting dalam berbagai bidang, seperti fisika, teknik, dan ilmu komputer. Fungsi sinus menghubungkan sudut dalam segitiga siku-siku dengan perbandingan sisi-sisinya.
Pengertian Sinus
Sinus dari suatu sudut dalam segitiga siku-siku didefinisikan sebagai perbandingan panjang sisi di hadapan sudut tersebut dengan panjang sisi miring segitiga tersebut. Sisi di hadapan sudut adalah sisi yang berlawanan dengan sudut tersebut, sedangkan sisi miring adalah sisi terpanjang dalam segitiga siku-siku, yaitu sisi yang berhadapan dengan sudut siku-siku.
Contoh Sederhana Pengertian Sinus
Misalnya, kita memiliki segitiga siku-siku dengan sudut A, sudut B, dan sudut C (sudut siku-siku). Sisi di hadapan sudut A adalah sisi BC, sisi di hadapan sudut B adalah sisi AC, dan sisi miring adalah sisi AB. Maka, sinus dari sudut A (sin A) adalah perbandingan panjang sisi BC dengan panjang sisi AB.
Rumus Sinus, Cosinus, dan Tangen
Berikut adalah tabel yang berisi rumus sinus, cosinus, dan tangen:
| Fungsi Trigonometri | Rumus |
|---|---|
| Sinus (sin) | sin A = sisi di hadapan sudut A / sisi miring |
| Cosinus (cos) | cos A = sisi di samping sudut A / sisi miring |
| Tangen (tan) | tan A = sisi di hadapan sudut A / sisi di samping sudut A |
Rumus Sinus
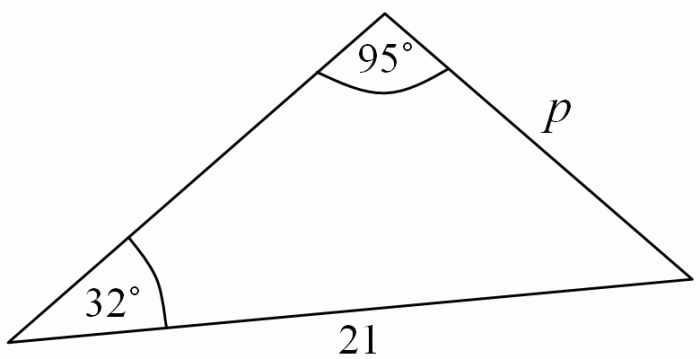
Sinus merupakan salah satu rasio trigonometri yang penting dalam matematika. Rumus sinus dapat digunakan untuk mencari panjang sisi segitiga siku-siku jika salah satu sudut dan sisi lain diketahui.
Rumus Sinus dalam Segitiga Siku-siku
Dalam segitiga siku-siku, sinus suatu sudut adalah perbandingan antara panjang sisi di hadapan sudut tersebut dengan panjang sisi miring.
sin A = sisi depan / sisi miring
di mana:
- A adalah sudut dalam segitiga siku-siku
- sisi depan adalah sisi yang berhadapan dengan sudut A
- sisi miring adalah sisi yang berhadapan dengan sudut siku-siku
Contoh Soal Mencari Sisi Miring Segitiga Siku-siku, Contoh soal sinus
Misalnya, kita memiliki segitiga siku-siku dengan sudut A = 30° dan sisi depan = 5 cm. Kita ingin mencari panjang sisi miring.
Dengan menggunakan rumus sinus, kita dapat menghitung sisi miring:
sin 30° = sisi depan / sisi miring
Kita tahu bahwa sin 30° = 1/2. Maka, kita dapat menulis:
1/2 = 5 cm / sisi miring
Untuk mencari sisi miring, kita dapat mengalikan kedua sisi persamaan dengan sisi miring dan kemudian membagi kedua sisi dengan 1/2.
sisi miring = 5 cm / (1/2) = 10 cm
Jadi, panjang sisi miring segitiga tersebut adalah 10 cm.
Menentukan Nilai Sinus untuk Sudut-sudut Istimewa
Nilai sinus untuk sudut-sudut istimewa (0°, 30°, 45°, 60°, 90°) dapat ditentukan dengan menggunakan tabel trigonometri atau dengan menggunakan segitiga siku-siku khusus.
Berikut adalah nilai sinus untuk sudut-sudut istimewa:
| Sudut | Nilai Sinus |
|---|---|
| 0° | 0 |
| 30° | 1/2 |
| 45° | √2/2 |
| 60° | √3/2 |
| 90° | 1 |
Nilai sinus untuk sudut-sudut istimewa ini sering digunakan dalam berbagai aplikasi matematika dan fisika.
Grafik Sinus
Grafik fungsi sinus merupakan representasi visual dari nilai fungsi sinus untuk berbagai sudut. Grafik ini memiliki pola berulang yang unik dan dapat digunakan untuk memahami perilaku fungsi sinus.
Menggambar Grafik Fungsi Sinus
Untuk menggambar grafik fungsi sinus y = sin x untuk satu periode, kita perlu memahami bahwa fungsi sinus memiliki periode 2π. Artinya, grafik fungsi sinus akan berulang setiap 2π radian. Berikut langkah-langkah untuk menggambar grafik fungsi sinus:
- Tentukan titik-titik penting pada satu periode, yaitu:
- Titik potong sumbu x: (0, 0), (π, 0), (2π, 0)
- Titik maksimum: (π/2, 1)
- Titik minimum: (3π/2, -1)
- Hubungkan titik-titik tersebut dengan kurva yang halus dan berulang untuk membentuk grafik fungsi sinus.
Identifikasi Amplitude, Periode, dan Titik Potong Sumbu X
Grafik fungsi sinus memiliki beberapa karakteristik penting, yaitu:
- Amplitude: Amplitude adalah jarak maksimum dari sumbu x ke titik tertinggi atau terendah pada grafik. Untuk fungsi y = sin x, amplitude-nya adalah 1.
- Periode: Periode adalah panjang satu siklus lengkap dari grafik. Untuk fungsi y = sin x, periodenya adalah 2π.
- Titik Potong Sumbu X: Titik potong sumbu x adalah titik-titik di mana grafik fungsi sinus memotong sumbu x. Untuk fungsi y = sin x, titik potong sumbu x adalah (nπ, 0), dengan n adalah bilangan bulat.
Pengaruh Perubahan Nilai a, b, c, dan d
Grafik fungsi sinus dapat dimodifikasi dengan menambahkan parameter a, b, c, dan d pada fungsi y = a sin (bx + c) + d. Berikut pengaruh masing-masing parameter:
- a: Nilai a menentukan amplitude grafik. Jika a > 1, amplitude akan lebih besar dari 1, dan jika 0 < a < 1, amplitude akan lebih kecil dari 1. Nilai a negatif akan menyebabkan grafik terbalik terhadap sumbu x.
- b: Nilai b menentukan periode grafik. Periode grafik adalah 2π/b. Jika b > 1, periode akan lebih kecil dari 2π, dan jika 0 < b < 1, periode akan lebih besar dari 2π.
- c: Nilai c menentukan pergeseran horizontal grafik. Grafik akan bergeser ke kiri sejauh c/b unit jika c > 0, dan bergeser ke kanan sejauh c/b unit jika c < 0.
- d: Nilai d menentukan pergeseran vertikal grafik. Grafik akan bergeser ke atas sejauh d unit jika d > 0, dan bergeser ke bawah sejauh d unit jika d < 0.
Penerapan Sinus
Sinus, salah satu fungsi trigonometri dasar, memiliki aplikasi yang luas dalam berbagai bidang, mulai dari fisika dan teknik hingga seni dan arsitektur. Fungsi sinus memungkinkan kita untuk memahami dan menghitung hubungan antara sudut dan sisi dalam segitiga siku-siku, yang pada gilirannya memungkinkan kita untuk memecahkan berbagai masalah yang melibatkan gerakan, jarak, dan tinggi.
Penerapan Sinus dalam Kehidupan Sehari-hari
Penerapan sinus dalam kehidupan sehari-hari dapat ditemukan di berbagai bidang, seperti:
- Fisika: Sinus digunakan dalam menghitung komponen vertikal dan horizontal gaya, percepatan, dan kecepatan dalam gerakan melingkar. Misalnya, pada gerakan bandul, sinus digunakan untuk menghitung kecepatan dan percepatan bandul pada titik tertentu.
- Teknik: Sinus digunakan dalam perhitungan struktur, seperti jembatan dan gedung. Misalnya, dalam perhitungan kekuatan struktur, sinus digunakan untuk menentukan tegangan dan regangan pada bahan.
- Seni: Sinus digunakan dalam seni untuk menciptakan efek visual yang menarik. Misalnya, dalam seni digital, sinus dapat digunakan untuk menghasilkan bentuk-bentuk gelombang dan pola yang unik.
Menghitung Tinggi Bangunan
Sinus dapat digunakan untuk menghitung tinggi bangunan dengan menggunakan sudut elevasi dan jarak dari bangunan. Misalnya, jika kita mengetahui sudut elevasi ke puncak bangunan adalah 30 derajat dan jarak dari bangunan adalah 50 meter, maka kita dapat menggunakan sinus untuk menghitung tinggi bangunan.
Sinus 30 derajat = Tinggi bangunan / Jarak dari bangunan
Tinggi bangunan = Sinus 30 derajat * Jarak dari bangunan
Tinggi bangunan = 0.5 * 50 meter = 25 meter
Menghitung Jarak
Sinus juga dapat digunakan untuk menghitung jarak dengan menggunakan sudut dan panjang sisi yang diketahui. Misalnya, jika kita mengetahui sudut elevasi ke puncak gunung adalah 45 derajat dan tinggi gunung adalah 1000 meter, maka kita dapat menggunakan sinus untuk menghitung jarak dari gunung.
Sinus 45 derajat = Tinggi gunung / Jarak dari gunung
Jarak dari gunung = Tinggi gunung / Sinus 45 derajat
Jarak dari gunung = 1000 meter / 0.707 = 1414 meter
Menghitung Kecepatan Benda
Sinus dapat digunakan untuk menghitung kecepatan benda dalam gerakan melingkar. Misalnya, jika kita mengetahui sudut yang ditempuh oleh benda dalam waktu tertentu dan jari-jari lingkaran, maka kita dapat menggunakan sinus untuk menghitung kecepatan benda.
Kecepatan = (Sudut / Waktu) * Jari-jari
Kecepatan = (Sinus (Sudut) * 2 * Pi * Jari-jari) / Waktu
Ilustrasi Sinus dalam Ayunan Sederhana
Ilustrasi berikut menunjukkan bagaimana sinus digunakan dalam menghitung panjang tali pada ayunan sederhana:
Bayangkan sebuah ayunan sederhana dengan panjang tali L dan sudut θ terhadap vertikal. Pada titik tertentu, ayunan memiliki perpindahan horizontal x dan perpindahan vertikal y.
Sinus sudut θ sama dengan perpindahan vertikal y dibagi dengan panjang tali L.
Sin θ = y / L
Dengan menggunakan persamaan ini, kita dapat menghitung panjang tali L jika kita mengetahui sudut θ dan perpindahan vertikal y.
Soal Latihan Sinus
Sinus merupakan salah satu konsep penting dalam trigonometri yang berhubungan dengan perbandingan sisi segitiga siku-siku. Penguasaan konsep sinus sangat penting untuk menyelesaikan berbagai masalah dalam matematika, fisika, dan bidang lainnya. Soal-soal latihan berikut ini akan membantu kamu dalam memahami dan menguasai konsep sinus.
Soal Latihan Sinus
Berikut ini adalah 5 soal latihan tentang sinus dengan berbagai tingkat kesulitan, lengkap dengan solusi dan penjelasannya.
| Soal | Solusi | Penjelasan |
|---|---|---|
| 1. Sebuah segitiga siku-siku memiliki sudut lancip 30° dan sisi miring 10 cm. Tentukan panjang sisi depan sudut 30°! | Sisi depan sudut 30° = 1/2 x sisi miring = 1/2 x 10 cm = 5 cm. | Dalam segitiga siku-siku, sinus sudut adalah perbandingan sisi depan sudut dengan sisi miring. Karena sinus 30° = 1/2, maka panjang sisi depan sudut 30° adalah setengah dari panjang sisi miring. |
| 2. Tentukan nilai sinus 45°! | Sinus 45° = √2 / 2 | Dalam segitiga siku-siku dengan sudut 45°, kedua sisi siku-siku memiliki panjang yang sama. Karena sinus sudut adalah perbandingan sisi depan sudut dengan sisi miring, maka sinus 45° = √2 / 2. |
| 3. Sebuah tangga dengan panjang 5 meter bersandar pada dinding. Jika sudut antara tangga dan tanah adalah 60°, tentukan tinggi tangga pada dinding! | Tinggi tangga pada dinding = 5 meter x sin 60° = 5 meter x √3 / 2 = 5√3 / 2 meter. | Sinus sudut adalah perbandingan sisi depan sudut dengan sisi miring. Dalam kasus ini, tinggi tangga pada dinding merupakan sisi depan sudut 60°, dan panjang tangga merupakan sisi miring. |
| 4. Tentukan nilai sinus 120°! | Sinus 120° = sin (180° – 60°) = sin 60° = √3 / 2 | Sudut 120° terletak di kuadran II. Pada kuadran II, sinus bernilai positif. Karena sinus 120° = sin (180° – 60°) = sin 60°, maka nilai sinus 120° = √3 / 2. |
| 5. Tentukan nilai sinus -30°! | Sinus -30° = -sin 30° = -1/2 | Sudut -30° terletak di kuadran IV. Pada kuadran IV, sinus bernilai negatif. Karena sinus -30° = -sin 30°, maka nilai sinus -30° = -1/2. |
Hubungan Sinus dengan Fungsi Trigonometri Lainnya
Sinus, cosinus, dan tangen adalah tiga fungsi trigonometri utama yang saling berhubungan erat. Hubungan antara ketiga fungsi ini dapat dipahami dengan mudah melalui konsep lingkaran satuan dan segitiga siku-siku.
Hubungan Sinus, Cosinus, dan Tangen
Hubungan antara sinus, cosinus, dan tangen dapat diringkas dalam rumus berikut:
tan θ = sin θ / cos θ
Rumus ini menunjukkan bahwa tangen suatu sudut adalah hasil bagi antara sinus sudut tersebut dengan cosinus sudut tersebut.
Contoh Soal
Misalnya, jika diketahui sin θ = 3/5 dan cos θ = 4/5, maka kita dapat menghitung tangen θ dengan menggunakan rumus di atas:
tan θ = sin θ / cos θ = (3/5) / (4/5) = 3/4
Diagram Hubungan Sinus, Cosinus, dan Tangen dalam Lingkaran Satuan
Diagram berikut menunjukkan hubungan antara sinus, cosinus, dan tangen dalam lingkaran satuan:
Gambar lingkaran satuan dengan titik (x,y) pada lingkaran. Titik (x,y) dihubungkan dengan titik (0,0) membentuk segitiga siku-siku. Sisi miring segitiga adalah jari-jari lingkaran satuan, yang bernilai 1. Sisi alas segitiga adalah x, dan sisi tegak segitiga adalah y. Sudut antara sumbu x positif dan sisi alas segitiga adalah θ.
Dalam diagram ini, sin θ diwakili oleh sisi tegak segitiga, cos θ diwakili oleh sisi alas segitiga, dan tan θ diwakili oleh perbandingan antara sisi tegak dan sisi alas segitiga.
Persamaan Trigonometri
Persamaan trigonometri adalah persamaan yang melibatkan fungsi trigonometri, seperti sinus, cosinus, dan tangen. Persamaan trigonometri yang melibatkan sinus adalah persamaan yang memuat fungsi sinus, seperti sin(x), sin(2x), atau sin(x/2).
Pengertian Persamaan Trigonometri yang Melibatkan Sinus
Persamaan trigonometri yang melibatkan sinus adalah persamaan yang memuat fungsi sinus. Fungsi sinus adalah fungsi yang menyatakan perbandingan antara sisi depan dan sisi miring dalam segitiga siku-siku. Persamaan trigonometri yang melibatkan sinus dapat berbentuk sederhana, seperti sin(x) = 1/2, atau lebih kompleks, seperti 2sin(2x) + 1 = 0.
Contoh Soal Persamaan Trigonometri yang Melibatkan Sinus
Berikut ini adalah contoh soal persamaan trigonometri yang melibatkan sinus:
Tentukan himpunan penyelesaian dari persamaan sin(x) = 1/2 untuk 0 ≤ x ≤ 2π.
Contoh soal sinus biasanya melibatkan perhitungan nilai sinus sudut tertentu atau mencari sudut yang memiliki nilai sinus tertentu. Soal-soal ini bisa ditemukan dalam berbagai konteks, seperti trigonometri, geometri, dan fisika. Nah, untuk memahami data secara visual, kita bisa menggunakan diagram ogive.
Ingin tahu lebih banyak tentang contoh soal ogive? Kamu bisa mengunjungi contoh soal ogive untuk mempelajari lebih lanjut. Setelah mempelajari ogive, kamu bisa mengaplikasikannya untuk menganalisis data yang berhubungan dengan contoh soal sinus, misalnya dalam menentukan distribusi sudut pada suatu objek.
Penyelesaian:
Untuk menyelesaikan persamaan sin(x) = 1/2, kita dapat menggunakan tabel nilai sinus atau rumus identitas trigonometri. Dalam tabel nilai sinus, kita dapat menemukan bahwa sin(π/6) = 1/2 dan sin(5π/6) = 1/2. Karena 0 ≤ x ≤ 2π, maka himpunan penyelesaiannya adalah π/6, 5π/6.
Cara Menyelesaikan Persamaan Trigonometri dengan Menggunakan Rumus Identitas Trigonometri
Untuk menyelesaikan persamaan trigonometri yang melibatkan sinus, kita dapat menggunakan rumus identitas trigonometri. Berikut ini adalah beberapa rumus identitas trigonometri yang dapat digunakan:
- sin2(x) + cos2(x) = 1
- sin(2x) = 2sin(x)cos(x)
- sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
Dengan menggunakan rumus identitas trigonometri, kita dapat mengubah persamaan trigonometri yang melibatkan sinus menjadi bentuk yang lebih sederhana sehingga lebih mudah untuk diselesaikan.
Aplikasi Sinus dalam Teknologi
Sinus, sebagai fungsi trigonometri, memiliki peran penting dalam berbagai bidang teknologi modern. Aplikasi sinus tidak terbatas pada matematika dan fisika, tetapi meluas ke dunia nyata, membentuk dasar dari berbagai perangkat dan sistem yang kita gunakan sehari-hari.
Pemrosesan Sinyal
Dalam pemrosesan sinyal, sinus digunakan untuk menganalisis dan memanipulasi sinyal analog, seperti suara, cahaya, dan sinyal elektromagnetik. Sinyal analog, yang bervariasi secara kontinu, dapat diuraikan menjadi kombinasi dari gelombang sinus dengan frekuensi dan amplitudo yang berbeda. Proses ini, yang dikenal sebagai analisis Fourier, memungkinkan kita untuk mengidentifikasi komponen frekuensi dalam sinyal dan memanipulasinya sesuai kebutuhan.
- Filter Sinyal: Filter elektronik, seperti filter low-pass dan high-pass, memanfaatkan sinus untuk memblokir atau melewatkan frekuensi tertentu dalam sinyal. Ini penting dalam audio, video, dan telekomunikasi untuk menghilangkan noise atau meningkatkan kualitas sinyal.
- Kompresi Audio: Algoritma kompresi audio, seperti MP3, menggunakan sinus untuk mewakili sinyal audio dengan lebih efisien. Dengan mengidentifikasi dan merepresentasikan hanya komponen frekuensi penting, mereka dapat mengurangi ukuran file audio tanpa kehilangan kualitas yang signifikan.
Telekomunikasi
Sinus adalah dasar dari komunikasi nirkabel modern. Gelombang elektromagnetik yang digunakan untuk mengirimkan data, seperti dalam jaringan seluler dan Wi-Fi, dapat dimodelkan menggunakan fungsi sinus. Frekuensi dan amplitudo gelombang sinus ini menentukan informasi yang ditransmisikan.
- Modulasi: Sinus digunakan dalam modulasi, proses yang menambahkan informasi ke sinyal pembawa. Dalam modulasi amplitudo (AM), amplitudo gelombang sinus diubah sesuai dengan sinyal informasi. Dalam modulasi frekuensi (FM), frekuensi gelombang sinus diubah.
- Antena: Antena, yang digunakan untuk mengirimkan dan menerima sinyal radio, dirancang berdasarkan prinsip-prinsip gelombang sinus. Bentuk dan ukuran antena menentukan frekuensi yang dapat mereka tangkap atau pancarkan.
Komputer Grafis
Sinus berperan penting dalam menciptakan efek visual yang realistis dalam komputer grafis. Fungsi sinus digunakan untuk menghasilkan gerakan, pencahayaan, dan tekstur yang halus dan alami.
- Animasi: Sinus digunakan untuk membuat gerakan berulang dan siklus, seperti gerakan ayunan pendulum, gelombang air, atau detak jantung. Dengan memanipulasi amplitudo dan frekuensi fungsi sinus, animator dapat menciptakan gerakan yang halus dan realistis.
- Pencahayaan: Sinus digunakan untuk menghitung intensitas cahaya yang dipantulkan dari permukaan objek. Dengan memodelkan pantulan cahaya sebagai gelombang sinus, para pengembang dapat menciptakan efek pencahayaan yang lebih realistis.
Contoh Aplikasi dalam Perangkat Elektronik
Sinus memiliki aplikasi yang luas dalam berbagai perangkat elektronik yang kita gunakan sehari-hari.
- Speaker: Speaker menggunakan magnet dan kumparan untuk mengubah sinyal listrik menjadi gelombang suara. Gelombang sinus yang dihasilkan oleh sinyal listrik menyebabkan kumparan bergetar, yang pada gilirannya menggetarkan udara dan menghasilkan suara.
- Mikrofon: Mikrofon mengubah gelombang suara menjadi sinyal listrik. Dalam mikrofon dinamis, gelombang suara menyebabkan diafragma bergetar, yang menggerakkan kumparan dalam medan magnet. Gerakan kumparan menghasilkan sinyal listrik yang sesuai dengan gelombang suara, yang sering kali berupa gelombang sinus.
- GPS: Sistem GPS menggunakan sinyal satelit untuk menentukan lokasi pengguna. Sinyal-sinyal ini dimodelkan menggunakan fungsi sinus, dan perangkat GPS menggunakan informasi ini untuk menghitung jarak dan posisi pengguna.
Ilustrasi Pembangkitan Gelombang Suara
Ilustrasi ini menunjukkan bagaimana sinus digunakan untuk menghasilkan gelombang suara. Gelombang sinus yang ditampilkan di sini mewakili sinyal listrik yang dikirim ke speaker. Amplitudo gelombang sinus menentukan volume suara, sementara frekuensi menentukan nada suara. Ketika sinyal listrik melewati speaker, diafragma speaker bergerak maju mundur sesuai dengan bentuk gelombang sinus, menghasilkan gelombang suara yang kita dengar.
Gambar ilustrasi: Sebuah gelombang sinus ditampilkan dengan sumbu horizontal mewakili waktu dan sumbu vertikal mewakili amplitudo. Gelombang sinus memiliki amplitudo yang bervariasi secara periodik, menunjukkan gerakan maju mundur diafragma speaker. Di bawah gelombang sinus, terdapat diagram sederhana speaker dengan diafragma yang bergerak maju mundur.
Sejarah Sinus
Konsep sinus dalam matematika memiliki sejarah panjang dan menarik, yang berakar pada zaman kuno. Perkembangan konsep sinus, seperti yang kita kenal sekarang, merupakan hasil dari kontribusi banyak ahli matematika dari berbagai budaya dan peradaban. Perjalanan ini mengantarkan kita pada pemahaman yang lebih dalam tentang trigonometri dan aplikasinya dalam berbagai bidang ilmu pengetahuan dan teknologi.
Perkembangan Awal Konsep Sinus
Konsep sinus pertama kali muncul dalam konteks astronomi di India kuno. Pada abad ke-2 SM, ahli matematika India, Hipparchus, menggunakan tabel korda untuk menghitung posisi bintang dan planet. Korda adalah garis lurus yang menghubungkan dua titik pada lingkaran, dan panjang korda ini terkait dengan sinus sudut yang dibentuk oleh dua jari-jari yang menghubungkan titik-titik tersebut ke pusat lingkaran. Namun, konsep sinus yang lebih modern baru muncul di India pada abad ke-5 Masehi.
- Pada abad ke-5 Masehi, ahli matematika India, Aryabhata, mengembangkan tabel sinus yang lebih lengkap dan akurat. Ia menggunakan konsep ‘ardha-jya’ (setengah korda) untuk menghitung nilai sinus. Konsep ini kemudian berkembang menjadi ‘jya’ (korda) yang menjadi dasar untuk pengembangan konsep sinus modern.
- Pada abad ke-7 Masehi, ahli matematika India, Brahmagupta, memperkenalkan konsep ‘jya-ardha’ (setengah korda) yang merupakan konsep yang sangat mirip dengan sinus modern. Ia juga mengembangkan rumus-rumus trigonometri yang melibatkan sinus, kosinus, dan tangen.
Peran Tokoh-Tokoh Penting
Seiring waktu, konsep sinus menyebar ke berbagai budaya dan peradaban, di mana para ahli matematika mengembangkan dan memperkaya konsep tersebut. Beberapa tokoh penting yang berperan dalam pengembangan konsep sinus antara lain:
- Muhammad ibn Musa al-Khwarizmi (780-850 M), seorang ahli matematika Persia, memperkenalkan konsep sinus dan kosinus ke dunia Islam. Ia menerjemahkan dan mengembangkan karya-karya matematikawan India, yang kemudian menyebar ke seluruh dunia Islam.
- Abu al-Wafa’ al-Buzjani (940-998 M), seorang ahli matematika Persia, mengembangkan tabel sinus yang lebih akurat dan memperkenalkan konsep tangen dan kotangen. Ia juga mengembangkan rumus-rumus trigonometri yang melibatkan sinus, kosinus, dan tangen.
- Nasir al-Din al-Tusi (1201-1274 M), seorang ahli matematika Persia, mengembangkan konsep sinus dan kosinus yang lebih modern. Ia juga mengembangkan tabel sinus yang sangat akurat, yang digunakan oleh para astronom dan ahli matematika selama berabad-abad.
- Georg von Peuerbach (1423-1461 M), seorang ahli matematika Austria, menerjemahkan dan mengembangkan karya-karya matematikawan Arab, termasuk tabel sinus. Ia juga mengembangkan tabel sinus yang lebih akurat dan memperkenalkan konsep tangen dan kotangen.
- Regiomontanus (1436-1476 M), seorang ahli matematika Jerman, mengembangkan konsep sinus dan kosinus yang lebih modern. Ia juga mengembangkan tabel sinus yang sangat akurat, yang digunakan oleh para astronom dan ahli matematika selama berabad-abad.
Timeline Perkembangan Konsep Sinus
Berikut adalah timeline yang menunjukkan perkembangan konsep sinus dari zaman kuno hingga saat ini:
| Zaman | Perkembangan | Tokoh |
|---|---|---|
| Abad ke-2 SM | Hipparchus menggunakan tabel korda untuk menghitung posisi bintang dan planet. | Hipparchus |
| Abad ke-5 Masehi | Aryabhata mengembangkan tabel sinus yang lebih lengkap dan akurat. | Aryabhata |
| Abad ke-7 Masehi | Brahmagupta memperkenalkan konsep ‘jya-ardha’ (setengah korda) yang merupakan konsep yang sangat mirip dengan sinus modern. | Brahmagupta |
| Abad ke-8 Masehi | Muhammad ibn Musa al-Khwarizmi memperkenalkan konsep sinus dan kosinus ke dunia Islam. | Muhammad ibn Musa al-Khwarizmi |
| Abad ke-10 Masehi | Abu al-Wafa’ al-Buzjani mengembangkan tabel sinus yang lebih akurat dan memperkenalkan konsep tangen dan kotangen. | Abu al-Wafa’ al-Buzjani |
| Abad ke-13 Masehi | Nasir al-Din al-Tusi mengembangkan konsep sinus dan kosinus yang lebih modern. | Nasir al-Din al-Tusi |
| Abad ke-15 Masehi | Georg von Peuerbach dan Regiomontanus mengembangkan tabel sinus yang lebih akurat dan memperkenalkan konsep tangen dan kotangen. | Georg von Peuerbach dan Regiomontanus |
| Abad ke-17 Masehi | Isaac Newton dan Gottfried Wilhelm Leibniz mengembangkan kalkulus, yang memungkinkan para matematikawan untuk menghitung nilai sinus dengan lebih akurat. | Isaac Newton dan Gottfried Wilhelm Leibniz |
| Abad ke-18 Masehi | Leonhard Euler mengembangkan rumus Euler, yang menghubungkan sinus dan kosinus dengan fungsi eksponensial. | Leonhard Euler |
| Abad ke-19 Masehi | Joseph Fourier mengembangkan deret Fourier, yang memungkinkan para matematikawan untuk menyatakan fungsi periodik, termasuk sinus, sebagai kombinasi linear dari fungsi sinus dan kosinus. | Joseph Fourier |
| Abad ke-20 Masehi | Perkembangan komputer memungkinkan para matematikawan untuk menghitung nilai sinus dengan lebih cepat dan akurat. | – |
Soal Sinus untuk Ujian
Sinus merupakan salah satu fungsi trigonometri yang penting dalam matematika dan fisika. Memahami konsep sinus dan penerapannya dalam berbagai situasi sangatlah krusial, baik untuk menyelesaikan masalah maupun untuk memahami fenomena alam. Soal-soal sinus dalam ujian biasanya dirancang untuk menguji pemahaman konsep dasar dan kemampuan untuk menerapkannya dalam berbagai konteks.
Artikel ini akan membahas contoh soal sinus yang sesuai untuk ujian dengan tingkat kesulitan sedang. Soal-soal ini dirancang untuk membantu siswa dalam mempersiapkan diri menghadapi ujian, sekaligus meningkatkan pemahaman mereka tentang konsep sinus.
Contoh Soal Sinus untuk Ujian
Berikut ini adalah contoh soal sinus yang dapat digunakan untuk ujian, beserta solusi dan penjelasannya:
| Soal | Solusi | Penjelasan |
|---|---|---|
| Diketahui segitiga siku-siku ABC dengan sudut siku-siku di C. Jika panjang sisi AB = 10 cm dan panjang sisi AC = 6 cm, tentukan nilai sinus sudut A. |
Langkah 1: Tentukan panjang sisi BC menggunakan teorema Pythagoras: BC2 = AB2 – AC2 BC2 = 102 – 62 BC2 = 100 – 36 BC2 = 64 BC = √64 = 8 cm Langkah 2: Hitung nilai sinus sudut A: sin A = BC / AB sin A = 8 / 10 sin A = 4/5 Jadi, nilai sinus sudut A adalah 4/5. |
Soal ini menguji pemahaman siswa tentang definisi sinus dalam segitiga siku-siku. Sinus sudut A didefinisikan sebagai perbandingan panjang sisi depan sudut A (BC) dengan panjang sisi miring (AB). Untuk menentukan nilai sinus, siswa harus terlebih dahulu menghitung panjang sisi BC menggunakan teorema Pythagoras. |
| Tentukan nilai sinus 30 derajat. |
Nilai sinus 30 derajat adalah 1/2. Ini merupakan nilai sinus sudut istimewa yang harus diingat. |
Soal ini menguji pengetahuan siswa tentang nilai sinus sudut istimewa. Sudut 30 derajat merupakan salah satu sudut istimewa yang nilai sinusnya harus diingat. |
| Diketahui fungsi f(x) = 2 sin (x + π/4). Tentukan nilai maksimum dan minimum dari fungsi tersebut. |
Langkah 1: Tentukan amplitudo fungsi. Amplitudo fungsi sinus adalah nilai mutlak dari koefisien sinus, yaitu 2 dalam kasus ini. Langkah 2: Tentukan nilai maksimum dan minimum fungsi. Nilai maksimum fungsi adalah amplitudo, yaitu 2. Nilai minimum fungsi adalah negatif dari amplitudo, yaitu -2. Jadi, nilai maksimum fungsi f(x) = 2 sin (x + π/4) adalah 2 dan nilai minimumnya adalah -2. |
Soal ini menguji pemahaman siswa tentang sifat-sifat fungsi sinus, khususnya amplitudo dan nilai maksimum/minimum. Siswa harus memahami bahwa amplitudo fungsi sinus menentukan rentang nilai fungsi tersebut. |
Ringkasan Penutup
Dengan memahami konsep sinus dan menguasai contoh soal yang diberikan, Anda akan memiliki fondasi yang kuat untuk mempelajari trigonometri lebih lanjut. Ingat, latihan adalah kunci untuk menguasai materi, jadi jangan ragu untuk mencoba menyelesaikan soal-soal latihan yang telah disediakan. Selamat belajar dan semoga sukses dalam mempelajari dunia trigonometri!






