Contoh soal tabel distribusi frekuensi data tunggal – Pernahkah kamu melihat kumpulan data yang terlihat membingungkan dan sulit dipahami? Tenang, ada cara untuk mengorganisir dan menganalisis data tersebut dengan mudah! Salah satunya adalah dengan menggunakan tabel distribusi frekuensi data tunggal. Dengan tabel ini, kamu dapat mengelompokkan data dan melihat pola yang tersembunyi di dalamnya.
Tabel distribusi frekuensi data tunggal adalah alat yang ampuh untuk menyederhanakan data dan memudahkan interpretasinya. Dalam artikel ini, kita akan membahas contoh soal tabel distribusi frekuensi data tunggal, langkah-langkah penyelesaiannya, dan manfaatnya dalam berbagai bidang.
Pengertian Tabel Distribusi Frekuensi Data Tunggal
Tabel distribusi frekuensi data tunggal merupakan alat bantu yang digunakan untuk menyusun data tunggal ke dalam kelompok-kelompok tertentu dan mencatat berapa kali setiap kelompok tersebut muncul dalam data. Dengan kata lain, tabel ini memberikan gambaran tentang sebaran data tunggal dengan mengelompokkan data serupa dan menghitung frekuensi kemunculannya.
Contoh Data Tunggal dan Tabel Distribusi Frekuensi
Misalnya, kita ingin menganalisis nilai ujian matematika dari 10 siswa:
- 70
- 80
- 75
- 85
- 90
- 70
- 80
- 85
- 75
- 90
Data ini dapat disusun dalam tabel distribusi frekuensi seperti berikut:
| Nilai Ujian | Frekuensi |
|---|---|
| 70 | 2 |
| 75 | 2 |
| 80 | 2 |
| 85 | 2 |
| 90 | 2 |
Manfaat Tabel Distribusi Frekuensi
Tabel distribusi frekuensi membantu kita memahami data tunggal dengan cara:
- Mempermudah pengelompokan data: Data yang banyak dan kompleks dapat dikelompokkan berdasarkan nilai atau kategori tertentu, sehingga lebih mudah dipahami.
- Menunjukkan pola data: Frekuensi kemunculan setiap kelompok data menunjukkan pola sebaran data, misalnya, apakah data terpusat pada nilai tertentu atau tersebar merata.
- Memudahkan analisis data: Dengan tabel distribusi frekuensi, kita dapat dengan mudah melihat nilai data yang paling sering muncul, rentang data, dan sebagainya.
Langkah-Langkah Menyusun Tabel Distribusi Frekuensi Data Tunggal: Contoh Soal Tabel Distribusi Frekuensi Data Tunggal
Tabel distribusi frekuensi merupakan alat yang penting dalam analisis data. Tabel ini membantu kita memahami pola dan kecenderungan dalam data tunggal dengan mengelompokkan data ke dalam kelas-kelas tertentu. Dengan menggunakan tabel distribusi frekuensi, kita dapat dengan mudah melihat sebaran data, frekuensi kemunculan setiap kelas, dan nilai-nilai yang paling sering muncul.
Langkah-Langkah Menyusun Tabel Distribusi Frekuensi Data Tunggal
Berikut adalah langkah-langkah yang diperlukan untuk menyusun tabel distribusi frekuensi data tunggal:
- Menentukan Rentang Data: Rentang data adalah selisih antara nilai data terbesar dan nilai data terkecil. Untuk menentukan rentang data, kita perlu mencari nilai data terbesar dan terkecil dalam kumpulan data. Contoh: Jika nilai data terbesar adalah 100 dan nilai data terkecil adalah 20, maka rentang datanya adalah 100 – 20 = 80.
- Menentukan Jumlah Kelas: Jumlah kelas dalam tabel distribusi frekuensi akan menentukan seberapa detail data yang akan kita tampilkan. Jumlah kelas dapat ditentukan dengan menggunakan rumus Sturges:
k = 1 + 3,322 log n
di mana k adalah jumlah kelas dan n adalah jumlah data. Sebagai contoh, jika kita memiliki 50 data, maka jumlah kelasnya adalah k = 1 + 3,322 log 50 ≈ 7.
- Menentukan Panjang Kelas: Panjang kelas adalah selisih antara batas atas dan batas bawah kelas. Panjang kelas dapat dihitung dengan membagi rentang data dengan jumlah kelas. Contoh: Jika rentang data adalah 80 dan jumlah kelas adalah 7, maka panjang kelasnya adalah 80 / 7 ≈ 11,43. Kita dapat membulatkan panjang kelas menjadi 12 untuk memudahkan perhitungan.
- Menentukan Batas Kelas: Batas kelas adalah nilai-nilai yang membatasi setiap kelas. Batas kelas bawah adalah nilai terkecil dalam kelas, sedangkan batas kelas atas adalah nilai terbesar dalam kelas. Batas kelas bawah kelas pertama biasanya sama dengan nilai data terkecil, sedangkan batas kelas atas kelas terakhir biasanya sama dengan nilai data terbesar.
- Contoh: Jika nilai data terkecil adalah 20 dan panjang kelas adalah 12, maka batas kelas bawah kelas pertama adalah 20, batas kelas atas kelas pertama adalah 31 (20 + 12 – 1), batas kelas bawah kelas kedua adalah 32 (31 + 1), batas kelas atas kelas kedua adalah 43 (32 + 12 – 1), dan seterusnya.
- Menentukan Titik Tengah Kelas: Titik tengah kelas adalah nilai tengah dari setiap kelas. Titik tengah kelas dapat dihitung dengan menjumlahkan batas kelas bawah dan batas kelas atas, kemudian dibagi dua. Contoh: Jika batas kelas bawah kelas pertama adalah 20 dan batas kelas atas kelas pertama adalah 31, maka titik tengah kelas pertama adalah (20 + 31) / 2 = 25,5.
- Menghitung Frekuensi: Frekuensi adalah jumlah data yang masuk ke dalam setiap kelas. Untuk menghitung frekuensi, kita perlu menghitung berapa banyak data yang berada di antara batas kelas bawah dan batas kelas atas setiap kelas. Contoh: Jika kita memiliki 50 data dan 10 data berada di antara batas kelas bawah dan batas kelas atas kelas pertama, maka frekuensi kelas pertama adalah 10.
- Menentukan Frekuensi Kumulatif: Frekuensi kumulatif adalah jumlah frekuensi dari semua kelas sebelumnya. Frekuensi kumulatif kelas pertama sama dengan frekuensi kelas pertama. Frekuensi kumulatif kelas kedua adalah jumlah frekuensi kelas pertama dan kelas kedua, dan seterusnya. Contoh: Jika frekuensi kelas pertama adalah 10 dan frekuensi kelas kedua adalah 15, maka frekuensi kumulatif kelas kedua adalah 10 + 15 = 25.
Contoh Penyusunan Tabel Distribusi Frekuensi
Misalkan kita memiliki data tunggal berikut:
20, 22, 25, 28, 30, 32, 35, 38, 40, 42, 45, 48, 50, 52, 55, 58, 60, 62, 65, 68, 70, 72, 75, 78, 80, 82, 85, 88, 90, 92, 95, 98, 100
Berikut adalah langkah-langkah penyusunan tabel distribusi frekuensi data tunggal:
- Menentukan Rentang Data: Nilai data terbesar adalah 100 dan nilai data terkecil adalah 20, maka rentang datanya adalah 100 – 20 = 80.
- Menentukan Jumlah Kelas: Jumlah data adalah 35, maka jumlah kelasnya adalah k = 1 + 3,322 log 35 ≈ 6.
- Menentukan Panjang Kelas: Panjang kelasnya adalah 80 / 6 ≈ 13,33. Kita dapat membulatkan panjang kelas menjadi 14 untuk memudahkan perhitungan.
- Menentukan Batas Kelas: Batas kelas bawah kelas pertama adalah 20, batas kelas atas kelas pertama adalah 33 (20 + 14 – 1), batas kelas bawah kelas kedua adalah 34 (33 + 1), batas kelas atas kelas kedua adalah 47 (34 + 14 – 1), dan seterusnya.
- Menentukan Titik Tengah Kelas: Titik tengah kelas pertama adalah (20 + 33) / 2 = 26,5, titik tengah kelas kedua adalah (34 + 47) / 2 = 40,5, dan seterusnya.
- Menghitung Frekuensi: Frekuensi kelas pertama adalah 5, frekuensi kelas kedua adalah 7, dan seterusnya.
- Menentukan Frekuensi Kumulatif: Frekuensi kumulatif kelas pertama adalah 5, frekuensi kumulatif kelas kedua adalah 12 (5 + 7), dan seterusnya.
Tabel distribusi frekuensi data tunggal untuk data di atas adalah sebagai berikut:
| Kelas | Batas Kelas Bawah | Batas Kelas Atas | Frekuensi |
|---|---|---|---|
| 1 | 20 | 33 | 5 |
| 2 | 34 | 47 | 7 |
| 3 | 48 | 61 | 8 |
| 4 | 62 | 75 | 7 |
| 5 | 76 | 89 | 5 |
| 6 | 90 | 103 | 3 |
Tabel distribusi frekuensi ini menunjukkan bahwa data terkonsentrasi di kelas 3 (48 – 61) dengan frekuensi 8. Kita juga dapat melihat bahwa frekuensi kumulatif meningkat secara bertahap, menunjukkan bahwa data terdistribusi secara merata.
Jenis-Jenis Data Tunggal
Dalam tabel distribusi frekuensi, data tunggal adalah data yang muncul hanya satu kali dalam suatu rentang data. Jenis data tunggal dapat dibedakan berdasarkan karakteristik dan sifatnya. Berikut adalah beberapa jenis data tunggal yang umum ditemukan dalam tabel distribusi frekuensi:
Data Tunggal Numerik
Data tunggal numerik adalah data tunggal yang berbentuk angka. Data ini dapat berupa bilangan bulat atau desimal. Contohnya, dalam data tinggi badan siswa kelas 7, jika ada satu siswa dengan tinggi badan 155 cm, maka 155 cm merupakan data tunggal numerik.
- Karakteristik: Data ini memiliki nilai yang pasti dan dapat diukur.
- Contoh: Tinggi badan, berat badan, skor ujian, nilai mata kuliah.
Data Tunggal Kategorikal
Data tunggal kategorikal adalah data tunggal yang berbentuk kategori atau label. Data ini tidak dapat diukur secara numerik. Contohnya, dalam data jenis kelamin siswa kelas 7, jika ada satu siswa dengan jenis kelamin perempuan, maka “perempuan” merupakan data tunggal kategorikal.
- Karakteristik: Data ini tidak memiliki nilai yang pasti dan tidak dapat diukur.
- Contoh: Jenis kelamin, warna rambut, warna mata, status pernikahan.
Data Tunggal Ordinal
Data tunggal ordinal adalah data tunggal yang berbentuk kategori yang memiliki urutan atau peringkat. Contohnya, dalam data peringkat siswa kelas 7, jika ada satu siswa dengan peringkat ke-5, maka “peringkat ke-5” merupakan data tunggal ordinal.
- Karakteristik: Data ini memiliki urutan atau peringkat, tetapi tidak memiliki nilai yang pasti dan tidak dapat diukur.
- Contoh: Tingkat kepuasan pelanggan, peringkat prestasi, kelas sosial.
| Jenis Data Tunggal | Contoh | Karakteristik |
|---|---|---|
| Numerik | Tinggi badan 170 cm | Nilai yang pasti dan dapat diukur |
| Kategorikal | Jenis kelamin perempuan | Tidak memiliki nilai yang pasti dan tidak dapat diukur |
| Ordinal | Peringkat ke-3 | Memiliki urutan atau peringkat, tetapi tidak memiliki nilai yang pasti dan tidak dapat diukur |
Contoh Soal Tabel Distribusi Frekuensi Data Tunggal
Tabel distribusi frekuensi data tunggal merupakan tabel yang menunjukkan frekuensi kemunculan setiap data tunggal dalam suatu kumpulan data. Tabel ini membantu dalam memahami pola distribusi data dan memudahkan analisis lebih lanjut. Berikut contoh soal tabel distribusi frekuensi data tunggal yang mencakup berbagai jenis data, lengkap dengan langkah-langkah penyelesaiannya.
Contoh Soal 1: Data Nilai Ujian
Misalkan terdapat data nilai ujian matematika dari 20 siswa sebagai berikut: 70, 80, 75, 85, 90, 70, 80, 75, 85, 90, 75, 80, 85, 90, 70, 80, 75, 85, 90, 80. Buatlah tabel distribusi frekuensi data tunggal dari data nilai ujian tersebut!
| Nilai | Frekuensi |
|---|---|
| 70 | 3 |
| 75 | 4 |
| 80 | 6 |
| 85 | 4 |
| 90 | 3 |
Langkah-langkah penyelesaian:
- Urutkan data nilai ujian dari yang terkecil hingga terbesar.
- Tentukan nilai yang berbeda (unique) dalam data, dalam contoh ini nilai yang berbeda adalah 70, 75, 80, 85, dan 90.
- Hitung frekuensi kemunculan setiap nilai yang berbeda. Misalnya, nilai 70 muncul sebanyak 3 kali, nilai 75 muncul sebanyak 4 kali, dan seterusnya.
- Buat tabel distribusi frekuensi dengan kolom nilai dan frekuensi. Masukkan nilai yang berbeda dan frekuensinya ke dalam tabel.
Contoh Soal 2: Data Tinggi Badan
Misalkan terdapat data tinggi badan (dalam cm) dari 15 orang sebagai berikut: 160, 165, 170, 165, 170, 160, 175, 165, 170, 160, 175, 165, 170, 175, 180. Buatlah tabel distribusi frekuensi data tunggal dari data tinggi badan tersebut!
| Tinggi Badan (cm) | Frekuensi |
|---|---|
| 160 | 3 |
| 165 | 4 |
| 170 | 4 |
| 175 | 3 |
| 180 | 1 |
Langkah-langkah penyelesaiannya sama dengan contoh soal 1, yaitu:
- Urutkan data tinggi badan dari yang terkecil hingga terbesar.
- Tentukan tinggi badan yang berbeda (unique) dalam data, dalam contoh ini tinggi badan yang berbeda adalah 160, 165, 170, 175, dan 180.
- Hitung frekuensi kemunculan setiap tinggi badan yang berbeda. Misalnya, tinggi badan 160 cm muncul sebanyak 3 kali, tinggi badan 165 cm muncul sebanyak 4 kali, dan seterusnya.
- Buat tabel distribusi frekuensi dengan kolom tinggi badan dan frekuensi. Masukkan tinggi badan yang berbeda dan frekuensinya ke dalam tabel.
Contoh Soal 3: Data Jenis Kelamin
Misalkan terdapat data jenis kelamin dari 10 orang sebagai berikut: Laki-laki, Perempuan, Laki-laki, Perempuan, Laki-laki, Perempuan, Laki-laki, Perempuan, Laki-laki, Perempuan. Buatlah tabel distribusi frekuensi data tunggal dari data jenis kelamin tersebut!
| Jenis Kelamin | Frekuensi |
|---|---|
| Laki-laki | 5 |
| Perempuan | 5 |
Langkah-langkah penyelesaiannya sama dengan contoh soal 1 dan 2, yaitu:
- Tentukan jenis kelamin yang berbeda (unique) dalam data, dalam contoh ini jenis kelamin yang berbeda adalah Laki-laki dan Perempuan.
- Hitung frekuensi kemunculan setiap jenis kelamin yang berbeda. Misalnya, jenis kelamin Laki-laki muncul sebanyak 5 kali, jenis kelamin Perempuan muncul sebanyak 5 kali.
- Buat tabel distribusi frekuensi dengan kolom jenis kelamin dan frekuensi. Masukkan jenis kelamin yang berbeda dan frekuensinya ke dalam tabel.
Manfaat Tabel Distribusi Frekuensi Data Tunggal
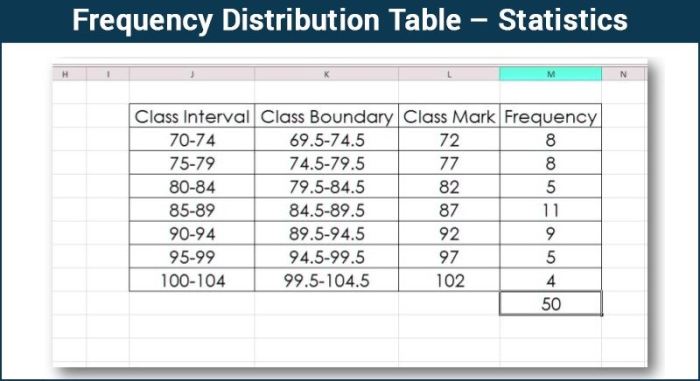
Tabel distribusi frekuensi data tunggal merupakan alat yang ampuh dalam analisis data. Dengan menyusun data ke dalam kelompok-kelompok, tabel ini membantu kita melihat pola dan tren yang tersembunyi dalam data mentah. Manfaatnya tidak hanya terbatas pada penyederhanaan data, tetapi juga memberikan pemahaman yang lebih dalam tentang karakteristik data.
Memudahkan Pemahaman Data, Contoh soal tabel distribusi frekuensi data tunggal
Salah satu manfaat utama tabel distribusi frekuensi adalah memudahkan pemahaman data. Data mentah yang banyak dan acak sulit dipahami, sedangkan tabel distribusi frekuensi menyusun data ke dalam kelas-kelas yang lebih terstruktur. Ini membantu kita melihat dengan jelas frekuensi kemunculan setiap nilai data dalam suatu rentang tertentu.
Contoh soal tabel distribusi frekuensi data tunggal biasanya berkaitan dengan menghitung frekuensi kemunculan data dalam rentang tertentu. Misalnya, kamu diminta untuk menghitung frekuensi skor ujian siswa dalam rentang nilai tertentu. Nah, setelah memahami konsep dasar tabel distribusi frekuensi, kamu bisa mencoba menganalisis data dari contoh soal iklan yang bisa kamu temukan di situs ini.
Contoh soal iklan ini bisa membantu kamu memahami bagaimana tabel distribusi frekuensi dapat digunakan untuk menganalisis data dalam dunia pemasaran. Dengan begitu, kamu akan lebih siap untuk mengerjakan contoh soal tabel distribusi frekuensi data tunggal dengan lebih baik.
Membantu Mengidentifikasi Pola dan Tren
Tabel distribusi frekuensi membantu kita mengidentifikasi pola dan tren dalam data. Dengan melihat frekuensi data dalam setiap kelas, kita dapat melihat distribusi data dan memahami bagaimana data tersebar. Misalnya, jika data terkonsentrasi di kelas tertentu, itu menunjukkan adanya pola atau kecenderungan dalam data.
Memudahkan Perbandingan Data
Tabel distribusi frekuensi memudahkan perbandingan data. Dengan menyusun data ke dalam kelas-kelas yang sama, kita dapat membandingkan distribusi data dari dua atau lebih kelompok. Ini membantu kita melihat perbedaan dan kesamaan antara kelompok-kelompok tersebut.
Memudahkan Perhitungan Statistik Deskriptif
Tabel distribusi frekuensi memudahkan perhitungan statistik deskriptif seperti rata-rata, median, modus, dan varians. Dengan tabel ini, kita dapat menghitung statistik deskriptif dengan lebih mudah dan akurat, tanpa harus bekerja dengan data mentah yang banyak.
Membantu dalam Pengambilan Keputusan
Tabel distribusi frekuensi memberikan informasi yang berharga untuk pengambilan keputusan. Dengan memahami pola dan tren dalam data, kita dapat membuat keputusan yang lebih tepat dan terinformasi. Misalnya, dalam bisnis, tabel distribusi frekuensi dapat membantu dalam menentukan strategi pemasaran yang efektif.
Contoh Konkrit
Misalnya, kita ingin menganalisis data tentang tinggi badan siswa di sebuah sekolah. Data mentah terdiri dari tinggi badan setiap siswa, yang mungkin sulit dipahami. Dengan menyusun data ke dalam tabel distribusi frekuensi, kita dapat melihat distribusi tinggi badan siswa. Misalnya, kita dapat melihat bahwa sebagian besar siswa memiliki tinggi badan di antara 160 cm dan 170 cm, sementara hanya sedikit siswa yang memiliki tinggi badan di bawah 150 cm atau di atas 180 cm. Informasi ini membantu kita memahami karakteristik tinggi badan siswa di sekolah tersebut.
Aplikasi Tabel Distribusi Frekuensi Data Tunggal
Tabel distribusi frekuensi data tunggal merupakan alat yang ampuh dalam menyusun dan menganalisis data yang dikumpulkan. Dengan mengelompokkan data ke dalam kelas-kelas tertentu, kita dapat melihat pola dan tren yang mungkin tidak terlihat jika data disajikan dalam bentuk mentah.
Kemampuan tabel distribusi frekuensi dalam meringkas data menjadikannya alat yang berguna dalam berbagai bidang, mulai dari penelitian ilmiah hingga pengambilan keputusan bisnis.
Contoh Aplikasi Tabel Distribusi Frekuensi Data Tunggal
Tabel distribusi frekuensi data tunggal memiliki banyak aplikasi dalam berbagai bidang, berikut beberapa contohnya:
- Pendidikan: Guru dapat menggunakan tabel distribusi frekuensi untuk menganalisis nilai ujian siswa. Dengan mengelompokkan nilai ke dalam kelas-kelas tertentu, guru dapat melihat sebaran nilai, mengidentifikasi siswa yang perlu bimbingan tambahan, dan mengevaluasi efektivitas metode pembelajaran.
- Kesehatan: Petugas kesehatan dapat menggunakan tabel distribusi frekuensi untuk menganalisis data pasien, seperti usia, tekanan darah, atau berat badan. Hal ini membantu mereka dalam mengidentifikasi tren dan pola penyakit, menentukan strategi pencegahan, dan memantau efektivitas pengobatan.
- Bisnis: Manajer dapat menggunakan tabel distribusi frekuensi untuk menganalisis data penjualan, seperti jumlah penjualan per hari, minggu, atau bulan. Informasi ini dapat membantu mereka dalam mengidentifikasi produk yang paling laris, mengoptimalkan strategi pemasaran, dan memprediksi tren penjualan di masa depan.
- Sosial: Peneliti sosial dapat menggunakan tabel distribusi frekuensi untuk menganalisis data survei, seperti pendapat masyarakat tentang isu-isu sosial, politik, atau ekonomi. Hasil analisis ini dapat memberikan gambaran tentang persepsi dan sikap masyarakat, yang berguna untuk membuat kebijakan publik yang lebih efektif.
Manfaat Tabel Distribusi Frekuensi dalam Pemecahan Masalah dan Pengambilan Keputusan
Tabel distribusi frekuensi membantu dalam memecahkan masalah dan mengambil keputusan dengan cara:
- Memudahkan Visualisasi Data: Tabel distribusi frekuensi menyajikan data dalam bentuk yang lebih mudah dipahami dan divisualisasikan, sehingga memudahkan dalam melihat pola dan tren yang mungkin tidak terlihat jika data disajikan dalam bentuk mentah.
- Mempermudah Analisis Data: Tabel distribusi frekuensi meringkas data menjadi bentuk yang lebih mudah dianalisis, sehingga memudahkan dalam menghitung statistik deskriptif seperti rata-rata, median, dan modus.
- Membantu dalam Pengambilan Keputusan: Informasi yang disajikan dalam tabel distribusi frekuensi dapat membantu dalam membuat keputusan yang lebih tepat, karena data yang disajikan lebih terstruktur dan mudah dipahami.
Pentingnya Tabel Distribusi Frekuensi Data Tunggal
Dalam dunia analisis data, tabel distribusi frekuensi data tunggal menjadi alat yang sangat berguna. Alat ini membantu kita untuk memahami pola dan tren dalam data dengan lebih baik, sehingga memudahkan kita dalam menarik kesimpulan yang lebih akurat. Tabel ini memberikan gambaran yang jelas tentang bagaimana data tersebar dan memberikan kita wawasan tentang frekuensi kemunculan setiap nilai dalam kumpulan data.
Memahami Pola dan Tren dalam Data
Tabel distribusi frekuensi data tunggal membantu kita memahami pola dan tren dalam data dengan mengelompokkan data ke dalam kelas-kelas tertentu. Dengan melihat frekuensi kemunculan data dalam setiap kelas, kita dapat mengidentifikasi nilai-nilai yang paling sering muncul, nilai-nilai yang jarang muncul, dan distribusi data secara keseluruhan.
Contoh Penerapan Tabel Distribusi Frekuensi
Misalnya, kita ingin menganalisis nilai ujian matematika dari 50 siswa. Dengan menggunakan tabel distribusi frekuensi, kita dapat mengelompokkan nilai ujian tersebut ke dalam kelas-kelas tertentu, seperti 0-20, 21-40, 41-60, 61-80, dan 81-100. Kemudian, kita dapat menghitung berapa banyak siswa yang mendapatkan nilai dalam setiap kelas. Dari tabel ini, kita dapat melihat dengan jelas bahwa sebagian besar siswa mendapatkan nilai di kelas 61-80, sementara hanya sedikit siswa yang mendapatkan nilai di kelas 0-20 dan 81-100.
Kesimpulan
Tabel distribusi frekuensi data tunggal adalah alat yang penting dalam analisis data karena membantu kita mengorganisir data, mengidentifikasi pola dan tren, dan membuat interpretasi yang tepat. Dengan memahami bagaimana data tersebar, kita dapat memperoleh pemahaman yang lebih baik tentang kumpulan data dan mengambil keputusan yang lebih tepat berdasarkan informasi yang diperoleh.
Kesulitan dalam Menyusun Tabel Distribusi Frekuensi Data Tunggal
Menyusun tabel distribusi frekuensi data tunggal mungkin terlihat mudah, namun ada beberapa kesulitan yang bisa dihadapi, terutama bagi pemula. Kesulitan ini bisa muncul dari berbagai faktor, mulai dari memahami konsep dasar hingga mengolah data dengan tepat.
Menentukan Banyaknya Kelas
Salah satu kesulitan yang sering dijumpai adalah menentukan banyaknya kelas yang tepat. Banyaknya kelas yang terlalu sedikit akan membuat data terlalu padat dan kurang detail, sementara terlalu banyak kelas akan membuat tabel terlalu kompleks dan sulit dipahami.
- Solusi: Untuk menentukan banyaknya kelas, bisa menggunakan rumus Sturges, yaitu:
K = 1 + 3.322 * log(n)
- Dimana K adalah banyaknya kelas dan n adalah jumlah data.
- Misalnya, jika terdapat 50 data, maka banyaknya kelas yang ideal adalah:
K = 1 + 3.322 * log(50) ≈ 7
Artinya, tabel distribusi frekuensi idealnya memiliki 7 kelas.
Menentukan Panjang Kelas
Kesulitan lain adalah menentukan panjang kelas yang tepat. Panjang kelas yang terlalu kecil akan membuat data terpecah-pecah dan kurang representatif, sementara terlalu besar akan membuat data terlalu umum dan kurang detail.
- Solusi: Panjang kelas dapat dihitung dengan rumus:
P = (Data Terbesar – Data Terkecil) / K
- Dimana P adalah panjang kelas, Data Terbesar adalah data terbesar dalam sampel, Data Terkecil adalah data terkecil dalam sampel, dan K adalah banyaknya kelas.
- Misalnya, jika data terbesar adalah 100 dan data terkecil adalah 20, dengan 7 kelas, maka panjang kelasnya adalah:
P = (100 – 20) / 7 ≈ 11.43
Panjang kelas sebaiknya dibulatkan ke angka yang mudah diinterpretasikan, misalnya 11 atau 12.
Menentukan Batas Kelas
Kesulitan selanjutnya adalah menentukan batas kelas yang tepat. Batas kelas harus jelas dan tidak tumpang tindih agar data dapat dikelompokkan dengan benar.
- Solusi: Untuk menentukan batas kelas, perlu diperhatikan:
- Batas kelas bawah kelas pertama harus lebih kecil dari data terkecil.
- Batas kelas atas kelas terakhir harus lebih besar dari data terbesar.
- Batas kelas atas kelas pertama harus sama dengan batas kelas bawah kelas kedua, dan seterusnya.
Contohnya, jika data terkecil adalah 20 dan data terbesar adalah 100, dengan panjang kelas 12, maka batas kelas bisa seperti ini:
| Kelas | Batas Kelas Bawah | Batas Kelas Atas |
|---|---|---|
| 1 | 18 | 29 |
| 2 | 30 | 41 |
| 3 | 42 | 53 |
| 4 | 54 | 65 |
| 5 | 66 | 77 |
| 6 | 78 | 89 |
| 7 | 90 | 101 |
Menghitung Frekuensi
Kesulitan terakhir adalah menghitung frekuensi data dalam setiap kelas. Frekuensi adalah jumlah data yang masuk dalam kelas tertentu.
- Solusi: Untuk menghitung frekuensi, bisa dilakukan dengan cara manual atau menggunakan software statistik.
- Cara manual, yaitu dengan menghitung satu per satu data yang masuk dalam kelas tertentu.
- Cara menggunakan software statistik, yaitu dengan memasukkan data ke dalam software dan software akan menghitung frekuensi secara otomatis.
Tips Menyusun Tabel Distribusi Frekuensi Data Tunggal
Tabel distribusi frekuensi data tunggal adalah alat yang efektif untuk menyajikan data dalam bentuk yang terstruktur dan mudah dipahami. Tabel ini membantu dalam mengorganisir data tunggal menjadi kelompok-kelompok yang lebih kecil, sehingga mudah untuk melihat pola dan tren dalam data. Menyusun tabel distribusi frekuensi yang baik membutuhkan pemahaman yang jelas tentang data dan tujuan analisis. Berikut adalah beberapa tips yang dapat membantu Anda dalam menyusun tabel distribusi frekuensi data tunggal yang akurat dan informatif.
Menentukan Interval Kelas
Interval kelas adalah rentang nilai yang digunakan untuk mengelompokkan data. Menentukan interval kelas yang tepat sangat penting untuk memastikan bahwa tabel distribusi frekuensi Anda efektif. Berikut adalah beberapa tips untuk menentukan interval kelas:
- Pertimbangkan rentang data: Rentang data adalah selisih antara nilai data terbesar dan terkecil. Interval kelas harus cukup besar untuk mencakup semua nilai data, tetapi tidak terlalu besar sehingga semua data dikelompokkan ke dalam satu kelas.
- Tentukan jumlah kelas: Jumlah kelas yang ideal biasanya antara 5 dan 15. Jumlah kelas yang terlalu sedikit dapat menyembunyikan pola dalam data, sedangkan jumlah kelas yang terlalu banyak dapat membuat tabel terlalu rumit.
- Pastikan interval kelas sama: Untuk menjaga konsistensi, interval kelas harus sama lebarnya.
Menentukan Titik Tengah Kelas
Titik tengah kelas adalah nilai tengah dari setiap interval kelas. Titik tengah kelas digunakan untuk menghitung statistik deskriptif seperti mean dan median.
- Hitung titik tengah kelas: Titik tengah kelas dapat dihitung dengan menjumlahkan batas bawah dan batas atas interval kelas, kemudian membaginya dengan 2.
- Gunakan titik tengah kelas untuk perhitungan: Titik tengah kelas digunakan untuk menghitung statistik deskriptif seperti mean dan median.
Menentukan Frekuensi
Frekuensi adalah jumlah data yang jatuh ke dalam setiap interval kelas. Frekuensi membantu Anda memahami distribusi data.
- Hitung frekuensi: Hitung jumlah data yang jatuh ke dalam setiap interval kelas. Anda dapat menggunakan tabel frekuensi untuk mencatat frekuensi setiap kelas.
- Verifikasi jumlah frekuensi: Pastikan jumlah frekuensi sama dengan jumlah total data.
Menyusun Tabel
Setelah menentukan interval kelas, titik tengah kelas, dan frekuensi, Anda dapat menyusun tabel distribusi frekuensi.
- Buat tabel: Gunakan tabel untuk menyajikan data yang terorganisir.
- Sertakan kolom untuk interval kelas, titik tengah kelas, dan frekuensi: Kolom-kolom ini memungkinkan Anda untuk dengan mudah melihat distribusi data.
- Berikan judul tabel: Judul tabel harus jelas dan deskriptif, sehingga pembaca dapat dengan mudah memahami isi tabel.
Menambahkan Kolom Tambahan
Anda dapat menambahkan kolom tambahan ke tabel distribusi frekuensi untuk memberikan informasi tambahan tentang data.
- Kolom frekuensi relatif: Kolom ini menunjukkan proporsi data yang jatuh ke dalam setiap interval kelas.
- Kolom frekuensi kumulatif: Kolom ini menunjukkan jumlah data yang jatuh ke dalam interval kelas tersebut dan semua interval kelas sebelumnya.
Menampilkan Tabel
Setelah tabel distribusi frekuensi Anda selesai, Anda dapat menampilkannya dalam berbagai cara.
- Gunakan grafik: Grafik seperti histogram atau poligon frekuensi dapat membantu memvisualisasikan distribusi data.
- Gunakan tabel: Tabel distribusi frekuensi dapat ditampilkan dalam bentuk tabel yang sederhana dan mudah dipahami.
Tips Tambahan
- Perhatikan skala: Pastikan skala pada tabel Anda sesuai dengan data Anda.
- Gunakan label yang jelas: Berikan label yang jelas untuk setiap kolom dan baris dalam tabel Anda.
- Perhatikan kejelasan: Pastikan tabel Anda mudah dibaca dan dipahami.
Terakhir
Dengan memahami cara menyusun dan menginterpretasikan tabel distribusi frekuensi data tunggal, kamu akan mampu melihat pola dan tren dalam data yang kompleks. Alat ini sangat berguna dalam berbagai bidang, seperti statistik, riset, dan bahkan dalam kehidupan sehari-hari. Jadi, jangan ragu untuk mempraktikkan dan menguasai teknik ini untuk mengoptimalkan analisis data kamu.




