Contoh soal tabel kebenaran – Tabel kebenaran adalah alat yang ampuh dalam logika proposisional. Dengan menggunakan tabel kebenaran, kita dapat menganalisis dan memahami hubungan antar pernyataan, menguji validitas argumen, dan menentukan kesetaraan logika. Tabel kebenaran membantu kita dalam memahami logika dengan cara yang terstruktur dan sistematis.
Dalam artikel ini, kita akan menjelajahi berbagai contoh soal tabel kebenaran, mulai dari yang sederhana hingga yang kompleks. Dengan mempelajari contoh-contoh ini, kita akan dapat menguasai konsep tabel kebenaran dan mengaplikasikannya dalam berbagai konteks logika.
Pengertian Tabel Kebenaran
Dalam dunia logika proposisional, tabel kebenaran menjadi alat penting untuk memahami nilai kebenaran dari pernyataan majemuk. Tabel kebenaran memungkinkan kita untuk menganalisis dan menentukan nilai kebenaran suatu pernyataan kompleks dengan cara yang sistematis dan mudah dipahami.
Pengertian Tabel Kebenaran
Tabel kebenaran adalah representasi tabular yang menunjukkan semua kemungkinan kombinasi nilai kebenaran untuk pernyataan-pernyataan dasar yang membentuk suatu pernyataan majemuk, dan nilai kebenaran dari pernyataan majemuk tersebut untuk setiap kombinasi nilai kebenaran tersebut.
Contoh Tabel Kebenaran
Sebagai contoh sederhana, perhatikan pernyataan “Jika hari hujan, maka saya memakai payung.” Pernyataan ini merupakan pernyataan majemuk yang terdiri dari dua pernyataan dasar: “Hari hujan” dan “Saya memakai payung”.
| Hari Hujan | Saya Memakai Payung | Jika Hari Hujan, Maka Saya Memakai Payung |
|---|---|---|
| Benar | Benar | Benar |
| Benar | Salah | Salah |
| Salah | Benar | Benar |
| Salah | Salah | Benar |
Tabel kebenaran di atas menunjukkan semua kemungkinan kombinasi nilai kebenaran untuk kedua pernyataan dasar tersebut. Sebagai contoh, baris pertama menunjukkan bahwa jika hari hujan (benar) dan saya memakai payung (benar), maka pernyataan majemuk “Jika hari hujan, maka saya memakai payung” juga benar.
Operator Logika
Operator logika adalah simbol atau kata yang digunakan untuk menghubungkan pernyataan-pernyataan logika, dan hasilnya adalah nilai kebenaran (benar atau salah). Operator logika ini penting dalam logika, matematika, dan ilmu komputer untuk membangun pernyataan yang lebih kompleks dan menganalisis hubungan antar pernyataan.
Tabel Kebenaran Operator Logika Dasar
Tabel kebenaran adalah alat yang berguna untuk memahami bagaimana operator logika bekerja. Tabel ini menunjukkan semua kemungkinan kombinasi nilai kebenaran untuk setiap pernyataan, dan nilai kebenaran hasil dari operasi logika tersebut.
| Operator | Simbol | Keterangan | Contoh Tabel Kebenaran | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Negasi | ¬ | Mengubah nilai kebenaran dari pernyataan menjadi kebalikannya. Jika pernyataan benar, negasinya salah, dan sebaliknya. |
|
|||||||||||||||
| Konjungsi | ∧ | Hanya benar jika kedua pernyataan yang dihubungkan benar. |
|
|||||||||||||||
| Disjungsi | ∨ | Benar jika setidaknya satu dari pernyataan yang dihubungkan benar. |
|
|||||||||||||||
| Implikasi | → | Hanya salah jika pernyataan pertama benar dan pernyataan kedua salah. |
|
|||||||||||||||
| Biimplikasi | ↔ | Benar jika kedua pernyataan yang dihubungkan memiliki nilai kebenaran yang sama (keduanya benar atau keduanya salah). |
|
Contoh Soal Tabel Kebenaran Sederhana
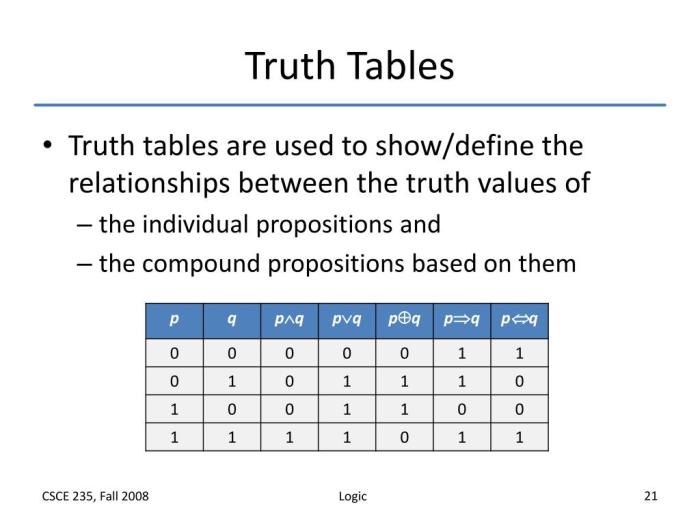
Tabel kebenaran merupakan alat yang sangat berguna dalam logika proposisional untuk menganalisis dan mengevaluasi kebenaran pernyataan majemuk. Dengan menggunakan tabel kebenaran, kita dapat menentukan nilai kebenaran dari suatu pernyataan majemuk berdasarkan nilai kebenaran dari pernyataan-pernyataan penyusunnya. Berikut ini adalah contoh soal tabel kebenaran sederhana untuk membantu Anda memahami konsep ini.
Contoh Soal 1: Pernyataan “p dan q”
Misalkan kita memiliki pernyataan “p dan q” dengan p: “Hari ini cerah” dan q: “Saya pergi ke pantai.” Untuk membuat tabel kebenaran, kita perlu mempertimbangkan semua kemungkinan kombinasi nilai kebenaran untuk p dan q. Karena p dan q adalah pernyataan sederhana, masing-masing dapat bernilai benar (T) atau salah (F).
| p | q | p dan q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Dari tabel di atas, dapat kita lihat bahwa pernyataan “p dan q” bernilai benar hanya jika p dan q keduanya bernilai benar. Jika salah satu atau keduanya bernilai salah, maka pernyataan “p dan q” juga bernilai salah.
Contoh Soal 2: Pernyataan “p atau q”
Misalkan kita memiliki pernyataan “p atau q” dengan p: “Saya makan nasi” dan q: “Saya makan mie.” Seperti pada contoh sebelumnya, kita perlu mempertimbangkan semua kemungkinan kombinasi nilai kebenaran untuk p dan q.
| p | q | p atau q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Dari tabel di atas, dapat kita lihat bahwa pernyataan “p atau q” bernilai benar jika salah satu atau keduanya bernilai benar. Pernyataan “p atau q” hanya bernilai salah jika p dan q keduanya bernilai salah.
Contoh Soal Tabel Kebenaran Kompleks
Tabel kebenaran adalah alat yang sangat berguna untuk menganalisis dan memahami logika proposisional. Dalam contoh-contoh sebelumnya, kita telah mempelajari bagaimana membuat tabel kebenaran untuk pernyataan sederhana. Namun, dalam logika, kita sering kali menghadapi pernyataan yang lebih kompleks yang melibatkan beberapa variabel proposisional dan operator logika. Dalam bagian ini, kita akan membahas beberapa contoh soal tabel kebenaran yang lebih kompleks.
Contoh Soal 1: Tabel Kebenaran untuk Pernyataan “Jika p maka q, dan r”
Pernyataan “Jika p maka q, dan r” merupakan contoh pernyataan kompleks yang melibatkan tiga variabel proposisional (p, q, r) dan dua operator logika (“jika…maka…” dan “dan”). Untuk membuat tabel kebenaran untuk pernyataan ini, kita perlu mempertimbangkan semua kemungkinan nilai kebenaran untuk p, q, dan r.
Misalkan:
- p: “Saya belajar”
- q: “Saya lulus ujian”
- r: “Saya senang”
Tabel kebenaran untuk pernyataan “Jika p maka q, dan r” adalah sebagai berikut:
| p | q | r | Jika p maka q | (Jika p maka q) dan r |
|---|---|---|---|---|
| B | B | B | B | B |
| B | B | S | B | S |
| B | S | B | S | S |
| B | S | S | S | S |
| S | B | B | B | B |
| S | B | S | B | S |
| S | S | B | B | B |
| S | S | S | B | S |
Dalam tabel ini, “B” mewakili nilai kebenaran “Benar” dan “S” mewakili nilai kebenaran “Salah”. Kolom “Jika p maka q” menunjukkan nilai kebenaran implikasi “Jika p maka q” untuk setiap kombinasi nilai kebenaran p dan q. Kolom “(Jika p maka q) dan r” menunjukkan nilai kebenaran konjungsi “Jika p maka q, dan r” untuk setiap kombinasi nilai kebenaran p, q, dan r.
Contoh Soal 2: Tabel Kebenaran untuk Pernyataan “p atau (q dan r)”
Pernyataan “p atau (q dan r)” merupakan contoh lain dari pernyataan kompleks yang melibatkan tiga variabel proposisional (p, q, r) dan dua operator logika (“atau” dan “dan”). Untuk membuat tabel kebenaran untuk pernyataan ini, kita perlu mempertimbangkan semua kemungkinan nilai kebenaran untuk p, q, dan r.
Contoh soal tabel kebenaran membantu kita memahami konsep logika proposisi. Dalam tabel kebenaran, kita bisa melihat nilai kebenaran dari pernyataan-pernyataan yang dirangkai dengan operator logika. Ingat, logika proposisi merupakan dasar penting dalam mempelajari berbagai bidang, termasuk komputer dan sistem informasi.
Nah, buat kamu yang ingin mendalami materi ini, coba deh cek contoh soal dan pembahasan tkpa yang bisa membantu kamu memahami konsep tabel kebenaran dan logika proposisi secara lebih mendalam. Dengan memahami konsep dasar logika proposisi, kamu bisa lebih mudah dalam memecahkan soal-soal yang berhubungan dengan tabel kebenaran dan berbagai materi logika lainnya.
Misalkan:
- p: “Saya makan apel”
- q: “Saya makan pisang”
- r: “Saya makan jeruk”
Tabel kebenaran untuk pernyataan “p atau (q dan r)” adalah sebagai berikut:
| p | q | r | q dan r | p atau (q dan r) |
|---|---|---|---|---|
| B | B | B | B | B |
| B | B | S | S | B |
| B | S | B | S | B |
| B | S | S | S | B |
| S | B | B | B | B |
| S | B | S | S | S |
| S | S | B | S | S |
| S | S | S | S | S |
Dalam tabel ini, “B” mewakili nilai kebenaran “Benar” dan “S” mewakili nilai kebenaran “Salah”. Kolom “q dan r” menunjukkan nilai kebenaran konjungsi “q dan r” untuk setiap kombinasi nilai kebenaran q dan r. Kolom “p atau (q dan r)” menunjukkan nilai kebenaran disjungsi “p atau (q dan r)” untuk setiap kombinasi nilai kebenaran p, q, dan r.
Penerapan Tabel Kebenaran
Tabel kebenaran adalah alat yang sangat berguna dalam logika, terutama untuk menganalisis dan memvalidasi argumen. Dengan menggunakan tabel kebenaran, kita dapat menentukan apakah suatu argumen valid atau tidak, dan juga dapat menguji kesetaraan logika dari dua pernyataan.
Validitas Argumen
Untuk menentukan validitas argumen, kita perlu memeriksa apakah kesimpulan argumen tersebut merupakan konsekuensi logis dari premis-premisnya. Dengan menggunakan tabel kebenaran, kita dapat menguji semua kemungkinan kombinasi nilai kebenaran untuk premis dan kesimpulan. Jika semua baris pada tabel kebenaran menunjukkan bahwa kesimpulan benar ketika semua premis benar, maka argumen tersebut valid.
Contoh:, Contoh soal tabel kebenaran
Misalkan kita memiliki argumen berikut:
Semua manusia adalah mamalia.
Semua mamalia adalah hewan.
Jadi, semua manusia adalah hewan.
Untuk menentukan validitas argumen ini, kita dapat membuat tabel kebenaran dengan tiga kolom, satu untuk setiap pernyataan. Kolom pertama mewakili premis pertama, kolom kedua mewakili premis kedua, dan kolom ketiga mewakili kesimpulan.
| Semua manusia adalah mamalia | Semua mamalia adalah hewan | Semua manusia adalah hewan |
|---|---|---|
| Benar | Benar | Benar |
| Benar | Salah | Salah |
| Salah | Benar | Salah |
| Salah | Salah | Salah |
Dari tabel kebenaran ini, kita dapat melihat bahwa kesimpulan benar ketika kedua premis benar. Oleh karena itu, argumen ini valid.
Kesetaraan Logika
Dua pernyataan dikatakan setara secara logika jika memiliki nilai kebenaran yang sama untuk setiap kombinasi nilai kebenaran dari variabel proposisional yang terlibat. Dengan menggunakan tabel kebenaran, kita dapat menguji kesetaraan logika dari dua pernyataan.
Contoh:, Contoh soal tabel kebenaran
Misalkan kita ingin menguji kesetaraan logika dari dua pernyataan berikut:
p → q
¬p ∨ q
Untuk menguji kesetaraan logika ini, kita dapat membuat tabel kebenaran dengan dua kolom, satu untuk setiap pernyataan. Kolom pertama mewakili p → q, dan kolom kedua mewakili ¬p ∨ q.
| p | q | p → q | ¬p ∨ q |
|---|---|---|---|
| Benar | Benar | Benar | Benar |
| Benar | Salah | Salah | Salah |
| Salah | Benar | Benar | Benar |
| Salah | Salah | Benar | Benar |
Dari tabel kebenaran ini, kita dapat melihat bahwa kedua pernyataan memiliki nilai kebenaran yang sama untuk setiap kombinasi nilai kebenaran dari p dan q. Oleh karena itu, kedua pernyataan tersebut setara secara logika.
Contoh Soal Tabel Kebenaran dengan Negasi
Dalam logika proposisional, negasi merupakan operasi yang mengubah nilai kebenaran suatu pernyataan. Jika pernyataan awalnya bernilai benar, maka negasinya bernilai salah, dan sebaliknya. Dalam tabel kebenaran, negasi direpresentasikan dengan simbol “¬”.
Berikut adalah contoh soal tabel kebenaran dengan negasi yang dapat membantu Anda memahami konsep ini:
Soal 1: Negasi Pernyataan Tunggal
Buat tabel kebenaran untuk pernyataan “¬p”, dengan p: “Saya suka makan cokelat.”
| p | ¬p |
|---|---|
| Benar | Salah |
| Salah | Benar |
Tabel kebenaran ini menunjukkan bahwa jika pernyataan “Saya suka makan cokelat” bernilai benar, maka negasinya “¬p” bernilai salah. Sebaliknya, jika pernyataan “Saya suka makan cokelat” bernilai salah, maka negasinya “¬p” bernilai benar.
Soal 2: Negasi Pernyataan Gabungan
Buat tabel kebenaran untuk pernyataan “¬(p dan q)”, dengan p: “Saya suka membaca buku” dan q: “Saya suka menonton film.”
| p | q | p dan q | ¬(p dan q) |
|---|---|---|---|
| Benar | Benar | Benar | Salah |
| Benar | Salah | Salah | Benar |
| Salah | Benar | Salah | Benar |
| Salah | Salah | Salah | Benar |
Tabel kebenaran ini menunjukkan bahwa negasi dari pernyataan gabungan “p dan q” bernilai benar jika dan hanya jika salah satu dari pernyataan p atau q bernilai salah, atau keduanya bernilai salah.
Contoh Soal Tabel Kebenaran dengan Konjungsi
Tabel kebenaran adalah alat yang sangat berguna dalam logika proposisional untuk menganalisis kebenaran pernyataan majemuk berdasarkan nilai kebenaran pernyataan-pernyataan penyusunnya. Salah satu operator logika yang sering digunakan adalah konjungsi, yang dilambangkan dengan “∧” dan diartikan sebagai “dan”.
Contoh Soal 1: “p dan q”
Berikut adalah contoh soal tabel kebenaran untuk pernyataan “p dan q”, dengan p: “Hari ini panas” dan q: “Saya minum es teh.”
| p | q | p ∧ q |
|---|---|---|
| Benar | Benar | Benar |
| Benar | Salah | Salah |
| Salah | Benar | Salah |
| Salah | Salah | Salah |
Dari tabel kebenaran ini, kita dapat melihat bahwa pernyataan “p dan q” hanya bernilai benar ketika kedua pernyataan p dan q bernilai benar. Jika salah satu atau keduanya bernilai salah, maka pernyataan “p dan q” juga bernilai salah.
Contoh Soal 2: “(p dan q) dan r”
Berikut adalah contoh soal tabel kebenaran untuk pernyataan “(p dan q) dan r”, dengan p: “Saya bangun pagi”, q: “Saya sarapan”, dan r: “Saya pergi ke sekolah.”
| p | q | r | p ∧ q | (p ∧ q) ∧ r |
|---|---|---|---|---|
| Benar | Benar | Benar | Benar | Benar |
| Benar | Benar | Salah | Benar | Salah |
| Benar | Salah | Benar | Salah | Salah |
| Benar | Salah | Salah | Salah | Salah |
| Salah | Benar | Benar | Salah | Salah |
| Salah | Benar | Salah | Salah | Salah |
| Salah | Salah | Benar | Salah | Salah |
| Salah | Salah | Salah | Salah | Salah |
Dalam tabel ini, kita dapat melihat bahwa pernyataan “(p dan q) dan r” hanya bernilai benar ketika semua pernyataan p, q, dan r bernilai benar. Jika salah satu atau lebih dari pernyataan tersebut bernilai salah, maka pernyataan “(p dan q) dan r” juga bernilai salah.
Contoh Soal Tabel Kebenaran dengan Disjungsi
Tabel kebenaran adalah alat yang sangat berguna dalam logika proposisional. Tabel kebenaran membantu kita untuk menganalisis dan memahami kebenaran suatu pernyataan kompleks dengan mencantumkan semua kemungkinan kombinasi nilai kebenaran untuk proposisi-proposisi yang terlibat. Disjungsi, yang dilambangkan dengan simbol “∨”, adalah salah satu konektor logika yang penting. Disjungsi menyatakan “atau”. Pernyataan “p ∨ q” benar jika setidaknya salah satu dari p atau q benar. Berikut adalah contoh soal tabel kebenaran dengan disjungsi.
Contoh Soal 1: “p atau q”
Misalkan p: “Saya suka bermain tenis” dan q: “Saya suka bermain badminton.”
Pernyataan “p atau q” berarti “Saya suka bermain tenis atau saya suka bermain badminton.”
Untuk membuat tabel kebenaran, kita perlu mencantumkan semua kemungkinan kombinasi nilai kebenaran untuk p dan q. Berikut adalah tabel kebenaran untuk pernyataan “p atau q”:
| p | q | p ∨ q |
|---|---|---|
| Benar | Benar | Benar |
| Benar | Salah | Benar |
| Salah | Benar | Benar |
| Salah | Salah | Salah |
Dari tabel kebenaran ini, kita dapat melihat bahwa pernyataan “p atau q” hanya salah jika kedua proposisi p dan q salah.
Contoh Soal 2: “(p atau q) atau r”
Misalkan p: “Saya belajar matematika”, q: “Saya belajar fisika”, dan r: “Saya belajar kimia.”
Pernyataan “(p atau q) atau r” berarti “Saya belajar matematika atau saya belajar fisika, atau saya belajar kimia.”
Untuk membuat tabel kebenaran, kita perlu mencantumkan semua kemungkinan kombinasi nilai kebenaran untuk p, q, dan r. Berikut adalah tabel kebenaran untuk pernyataan “(p atau q) atau r”:
| p | q | r | (p ∨ q) | (p ∨ q) ∨ r |
|---|---|---|---|---|
| Benar | Benar | Benar | Benar | Benar |
| Benar | Benar | Salah | Benar | Benar |
| Benar | Salah | Benar | Benar | Benar |
| Benar | Salah | Salah | Benar | Benar |
| Salah | Benar | Benar | Benar | Benar |
| Salah | Benar | Salah | Benar | Benar |
| Salah | Salah | Benar | Salah | Benar |
| Salah | Salah | Salah | Salah | Salah |
Dari tabel kebenaran ini, kita dapat melihat bahwa pernyataan “(p atau q) atau r” hanya salah jika ketiga proposisi p, q, dan r salah.
Contoh Soal Tabel Kebenaran dengan Implikasi
Tabel kebenaran merupakan alat yang sangat berguna untuk menganalisis dan memahami pernyataan-pernyataan logika. Dalam tabel kebenaran, setiap pernyataan diuji dengan semua kemungkinan nilai kebenarannya, sehingga kita dapat mengetahui nilai kebenaran dari pernyataan yang lebih kompleks yang dibangun dari pernyataan-pernyataan tersebut.
Salah satu jenis pernyataan logika yang penting adalah implikasi. Implikasi adalah pernyataan yang menyatakan bahwa jika suatu pernyataan benar, maka pernyataan lainnya juga benar. Simbol untuk implikasi adalah “→”.
Contoh Soal 1
Soal pertama kita adalah membuat tabel kebenaran untuk pernyataan “Jika p maka q”, dengan p: “Saya belajar dengan giat” dan q: “Saya mendapatkan nilai bagus.” Berikut langkah-langkahnya:
- Identifikasi variabel-variabel yang terlibat dalam pernyataan. Dalam kasus ini, variabel-variabelnya adalah p dan q.
- Buat tabel dengan kolom untuk setiap variabel dan kolom untuk pernyataan implikasi (p → q).
- Tuliskan semua kemungkinan kombinasi nilai kebenaran untuk p dan q. Karena setiap variabel memiliki dua kemungkinan nilai kebenaran (benar atau salah), maka ada 22 = 4 kemungkinan kombinasi.
- Hitung nilai kebenaran untuk pernyataan implikasi (p → q) untuk setiap kombinasi nilai kebenaran p dan q. Ingat bahwa implikasi hanya salah jika pernyataan pertama benar dan pernyataan kedua salah.
| p | q | p → q |
|---|---|---|
| Benar | Benar | Benar |
| Benar | Salah | Salah |
| Salah | Benar | Benar |
| Salah | Salah | Benar |
Contoh Soal 2
Soal kedua kita adalah membuat tabel kebenaran untuk pernyataan “Jika (p dan q) maka r”, dengan p: “Saya makan nasi”, q: “Saya makan sayur”, dan r: “Saya kenyang.” Berikut langkah-langkahnya:
- Identifikasi variabel-variabel yang terlibat dalam pernyataan. Dalam kasus ini, variabel-variabelnya adalah p, q, dan r.
- Buat tabel dengan kolom untuk setiap variabel dan kolom untuk pernyataan implikasi ((p dan q) → r).
- Tuliskan semua kemungkinan kombinasi nilai kebenaran untuk p, q, dan r. Karena setiap variabel memiliki dua kemungkinan nilai kebenaran (benar atau salah), maka ada 23 = 8 kemungkinan kombinasi.
- Hitung nilai kebenaran untuk pernyataan (p dan q) untuk setiap kombinasi nilai kebenaran p dan q. Ingat bahwa konjungsi (dan) hanya benar jika kedua pernyataan benar.
- Hitung nilai kebenaran untuk pernyataan implikasi ((p dan q) → r) untuk setiap kombinasi nilai kebenaran (p dan q) dan r. Ingat bahwa implikasi hanya salah jika pernyataan pertama benar dan pernyataan kedua salah.
| p | q | r | (p dan q) | (p dan q) → r |
|---|---|---|---|---|
| Benar | Benar | Benar | Benar | Benar |
| Benar | Benar | Salah | Benar | Salah |
| Benar | Salah | Benar | Salah | Benar |
| Benar | Salah | Salah | Salah | Benar |
| Salah | Benar | Benar | Salah | Benar |
| Salah | Benar | Salah | Salah | Benar |
| Salah | Salah | Benar | Salah | Benar |
| Salah | Salah | Salah | Salah | Benar |
Ringkasan Terakhir
Memahami tabel kebenaran adalah langkah penting dalam memahami logika. Dengan menggunakan tabel kebenaran, kita dapat menganalisis pernyataan, menguji argumen, dan menemukan kesetaraan logika. Dengan mempelajari contoh-contoh soal yang telah diuraikan, kita dapat memperoleh pemahaman yang lebih dalam tentang logika dan mengaplikasikannya dalam berbagai bidang, seperti ilmu komputer, matematika, dan filsafat.