Contoh soal tentang matriks – Pernahkah Anda mendengar tentang matriks? Dalam matematika, matriks adalah susunan bilangan yang disusun dalam baris dan kolom. Konsep ini mungkin terdengar rumit, tapi sebenarnya matriks punya banyak aplikasi menarik dalam kehidupan sehari-hari, mulai dari ekonomi hingga komputer grafis. Bayangkan saja, bagaimana komputer mampu menampilkan gambar 3D yang realistis? Rahasianya terletak pada penggunaan matriks!
Di artikel ini, kita akan menjelajahi dunia matriks melalui contoh soal yang mudah dipahami. Anda akan belajar tentang berbagai jenis matriks, operasi matriks, determinan, invers, dan aplikasi praktisnya. Siap-siap untuk menjelajahi dunia matriks yang penuh dengan keajaiban!
Pengertian Matriks: Contoh Soal Tentang Matriks
Matriks merupakan suatu susunan bilangan yang disusun dalam bentuk baris dan kolom. Matriks sangat penting dalam berbagai bidang ilmu seperti matematika, fisika, kimia, ekonomi, dan komputer. Dalam matematika, matriks digunakan untuk menyelesaikan sistem persamaan linear, transformasi geometri, dan banyak lagi.
Contoh Matriks
Contoh matriks adalah sebagai berikut:
A =
$$\beginbmatrix 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \endbmatrix$$
Matriks A di atas memiliki 3 baris dan 3 kolom. Ordo dari matriks A adalah 3 x 3. Elemen-elemen dari matriks A adalah bilangan 1, 2, 3, 4, 5, 6, 7, 8, dan 9.
Jenis-Jenis Matriks
Berikut adalah beberapa jenis matriks beserta contohnya:
| Jenis Matriks | Contoh | Keterangan |
|---|---|---|
| Matriks Persegi | $$\beginbmatrix 1 & 2 \\ 3 & 4 \endbmatrix$$ | Matriks yang memiliki jumlah baris dan kolom yang sama. |
| Matriks Nol | $$\beginbmatrix 0 & 0 \\ 0 & 0 \endbmatrix$$ | Matriks yang semua elemennya bernilai 0. |
| Matriks Identitas | $$\beginbmatrix 1 & 0 \\ 0 & 1 \endbmatrix$$ | Matriks persegi dengan elemen diagonal utama bernilai 1 dan elemen lainnya bernilai 0. |
| Matriks Diagonal | $$\beginbmatrix 1 & 0 \\ 0 & 4 \endbmatrix$$ | Matriks persegi dengan elemen non-diagonal bernilai 0. |
| Matriks Segitiga Atas | $$\beginbmatrix 1 & 2 & 3 \\ 0 & 4 & 5 \\ 0 & 0 & 6 \endbmatrix$$ | Matriks persegi dengan elemen di bawah diagonal utama bernilai 0. |
| Matriks Segitiga Bawah | $$\beginbmatrix 1 & 0 & 0 \\ 2 & 3 & 0 \\ 4 & 5 & 6 \endbmatrix$$ | Matriks persegi dengan elemen di atas diagonal utama bernilai 0. |
| Matriks Transpose | $$\beginbmatrix 1 & 2 \\ 3 & 4 \endbmatrix^T = \beginbmatrix 1 & 3 \\ 2 & 4 \endbmatrix$$ | Matriks yang diperoleh dengan menukar baris dan kolom dari matriks aslinya. |
Operasi Matriks
Setelah mempelajari definisi dan jenis-jenis matriks, kita akan menjelajahi berbagai operasi yang dapat dilakukan pada matriks. Operasi matriks ini memiliki peran penting dalam berbagai bidang seperti matematika, fisika, ekonomi, dan ilmu komputer.
Penjumlahan Matriks
Penjumlahan matriks adalah operasi yang menggabungkan dua matriks dengan dimensi yang sama. Untuk menjumlahkan dua matriks, kita menjumlahkan elemen-elemen yang memiliki posisi yang sama dalam kedua matriks tersebut.
- Syarat penjumlahan matriks adalah kedua matriks harus memiliki ordo yang sama.
- Hasil penjumlahan matriks adalah matriks baru dengan ordo yang sama dengan matriks yang dijumlahkan.
Perkalian Matriks dengan Skalar
Perkalian matriks dengan skalar adalah operasi yang mengalikan setiap elemen matriks dengan skalar tersebut. Skalar adalah bilangan real yang tidak memiliki dimensi.
- Hasil perkalian matriks dengan skalar adalah matriks baru dengan ordo yang sama dengan matriks awal.
- Setiap elemen dalam matriks hasil perkalian adalah hasil perkalian elemen matriks awal dengan skalar.
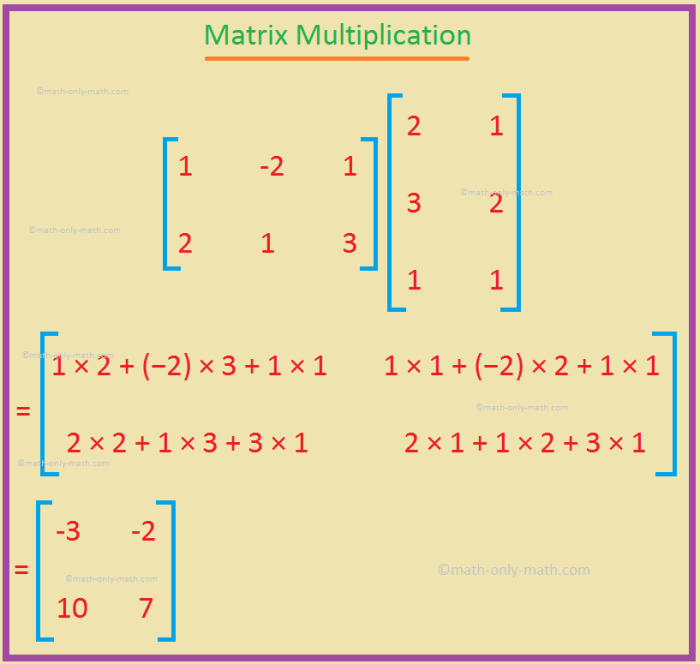
Perkalian Matriks dengan Matriks Lain
Perkalian matriks dengan matriks lain adalah operasi yang lebih kompleks daripada penjumlahan matriks atau perkalian matriks dengan skalar. Syarat perkalian matriks adalah jumlah kolom matriks pertama harus sama dengan jumlah baris matriks kedua.
- Hasil perkalian matriks adalah matriks baru dengan jumlah baris sama dengan matriks pertama dan jumlah kolom sama dengan matriks kedua.
- Elemen pada baris ke-i dan kolom ke-j dari matriks hasil perkalian dihitung dengan menjumlahkan hasil perkalian elemen-elemen pada baris ke-i dari matriks pertama dengan elemen-elemen pada kolom ke-j dari matriks kedua.
Determinan Matriks
Determinan matriks adalah sebuah nilai skalar yang dikaitkan dengan matriks persegi. Nilai ini dapat digunakan untuk menyelesaikan sistem persamaan linear, menentukan invers matriks, dan dalam berbagai aplikasi matematika lainnya.
Determinan Matriks 2×2
Determinan matriks 2×2 dihitung dengan rumus berikut:
Determinan matriks
A =
[ a b ]
[ c d ]
adalah det(A) = ad – bc
Contohnya, jika kita memiliki matriks:
A =
[ 2 3 ]
[ 1 4 ]
Maka determinannya adalah:
det(A) = (2 * 4) – (3 * 1) = 8 – 3 = 5
Determinan Matriks 3×3
Untuk menghitung determinan matriks 3×3, kita dapat menggunakan metode ekspansi kofaktor. Metode ini melibatkan penguraian matriks 3×3 menjadi tiga matriks 2×2, dan kemudian menghitung determinan masing-masing matriks 2×2.
Berikut adalah contoh soal tentang menghitung determinan matriks 3×3:
Hitunglah determinan dari matriks:
A =
[ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
Untuk menghitung determinan, kita dapat menggunakan ekspansi kofaktor pada baris pertama:
det(A) = 1 * det([ 5 6 ]
[ 8 9 ]) – 2 * det([ 4 6 ]
[ 7 9 ]) + 3 * det([ 4 5 ]
[ 7 8 ])
Kemudian, kita menghitung determinan matriks 2×2:
det(A) = 1 * (5 * 9 – 6 * 8) – 2 * (4 * 9 – 6 * 7) + 3 * (4 * 8 – 5 * 7)
= 1 * (-3) – 2 * (-6) + 3 * (-3)
= -3 + 12 – 9
= 0
Determinan Matriks dan Invers Matriks
Determinan matriks berhubungan erat dengan invers matriks. Sebuah matriks persegi memiliki invers jika dan hanya jika determinannya tidak sama dengan nol.
Invers matriks adalah matriks yang, ketika dikalikan dengan matriks aslinya, menghasilkan matriks identitas. Invers matriks dapat dihitung dengan menggunakan rumus berikut:
A⁻¹ = (1/det(A)) * adj(A)
Dimana:
- A⁻¹ adalah invers matriks A
- det(A) adalah determinan matriks A
- adj(A) adalah adjoin matriks A
Adjoin matriks A adalah transpos dari matriks kofaktor A. Kofaktor dari elemen matriks adalah determinan dari sub-matriks yang dihasilkan dengan menghapus baris dan kolom elemen tersebut, dikalikan dengan (-1)^(i+j), di mana i dan j adalah indeks baris dan kolom elemen tersebut.
Invers Matriks
Invers matriks adalah matriks yang ketika dikalikan dengan matriks asalnya akan menghasilkan matriks identitas. Matriks identitas adalah matriks persegi dengan semua elemen diagonal utamanya bernilai 1 dan elemen lainnya bernilai 0. Invers matriks hanya ada jika determinan matriks tersebut tidak sama dengan nol.
Mencari Invers Matriks 2×2
Untuk mencari invers matriks 2×2, kita dapat menggunakan rumus berikut:
Invers dari matriks
a b c d adalah:
d -b -c a di mana 1/(ad-bc) adalah determinan matriks.
Contohnya, untuk mencari invers dari matriks:
| 2 | 3 |
| 1 | 4 |
Pertama, kita hitung determinannya:
(2)(4) – (3)(1) = 5
Kemudian, kita gunakan rumus di atas untuk mencari inversnya:
| 4 | -3 |
| -1 | 2 |
Diperoleh hasil:
| 1/5 | -3/5 |
| -1/5 | 2/5 |
Contoh Soal Mencari Invers Matriks 3×3
Carilah invers dari matriks:
| 1 | 2 | 3 |
| 0 | 1 | 4 |
| 5 | 6 | 0 |
Syarat Suatu Matriks Memiliki Invers
Suatu matriks memiliki invers jika dan hanya jika determinannya tidak sama dengan nol. Determinan matriks adalah nilai skalar yang dihitung dari elemen-elemen matriks tersebut. Jika determinan matriks sama dengan nol, maka matriks tersebut tidak memiliki invers.
Sistem Persamaan Linear
Sistem persamaan linear adalah kumpulan persamaan linear yang melibatkan variabel yang sama. Matriks dapat digunakan sebagai alat yang efektif untuk menyelesaikan sistem persamaan linear, khususnya ketika kita berhadapan dengan sistem persamaan yang melibatkan banyak variabel.
Cara Menyelesaikan Sistem Persamaan Linear dengan Matriks
Untuk menyelesaikan sistem persamaan linear dengan matriks, kita dapat menggunakan metode matriks terbalik atau metode eliminasi Gauss-Jordan.
- Metode Matriks Terbalik: Dalam metode ini, kita mengubah sistem persamaan linear menjadi bentuk matriks AX = B, di mana A adalah matriks koefisien, X adalah matriks variabel, dan B adalah matriks konstanta. Kemudian, kita mencari invers dari matriks A, yaitu A-1. Solusi sistem persamaan linear diperoleh dengan mengalikan kedua ruas persamaan dengan A-1, sehingga X = A-1B.
- Metode Eliminasi Gauss-Jordan: Metode ini melibatkan operasi baris elementer pada matriks yang diperluas, yang merupakan gabungan matriks koefisien dan matriks konstanta. Operasi baris elementer ini bertujuan untuk mengubah matriks yang diperluas menjadi bentuk eselon baris tereduksi (Reduced Row Echelon Form, RREF), di mana solusi sistem persamaan linear dapat langsung dibaca.
Contoh Soal Sistem Persamaan Linear 2 Variabel
Misalkan kita memiliki sistem persamaan linear berikut:
2x + 3y = 7
x – y = 1
Untuk menyelesaikan sistem persamaan linear ini dengan metode matriks, kita dapat menulisnya dalam bentuk matriks:
2 3 7 1 -1 1
Kita dapat menggunakan metode eliminasi Gauss-Jordan untuk menyelesaikan sistem persamaan linear ini. Operasi baris elementer yang dapat dilakukan meliputi:
- Menukar dua baris
- Mengalikan baris dengan konstanta non-nol
- Menambahkan kelipatan satu baris ke baris lain
Tujuannya adalah untuk mengubah matriks yang diperluas menjadi bentuk eselon baris tereduksi (RREF). Dalam bentuk RREF, matriks koefisien akan menjadi matriks identitas, dan solusi sistem persamaan linear dapat langsung dibaca dari kolom konstanta.
Contoh soal tentang matriks biasanya melibatkan operasi seperti penjumlahan, pengurangan, perkalian, dan determinan. Nah, kalau kamu lagi belajar tentang kurs jual dan kurs beli, kamu bisa coba cari contoh soal di contoh soal kurs jual dan kurs beli untuk melatih kemampuanmu dalam menghitung nilai tukar mata uang.
Soal-soal tentang kurs jual dan kurs beli ini sebenarnya bisa juga dihubungkan dengan konsep matriks, lho! Misalnya, kamu bisa membuat matriks untuk merepresentasikan nilai tukar mata uang berbagai negara. Seru, kan?
Metode Eliminasi Gauss-Jordan
Metode eliminasi Gauss-Jordan adalah metode sistematis untuk menyelesaikan sistem persamaan linear dengan menggunakan operasi baris elementer pada matriks yang diperluas. Langkah-langkah dalam metode ini adalah:
- Tulis sistem persamaan linear dalam bentuk matriks yang diperluas. Matriks yang diperluas adalah gabungan matriks koefisien dan matriks konstanta.
- Ubah matriks yang diperluas menjadi bentuk eselon baris tereduksi (RREF). Ini dilakukan dengan melakukan operasi baris elementer pada matriks yang diperluas.
- Baca solusi sistem persamaan linear dari bentuk RREF. Solusi dapat dibaca langsung dari kolom konstanta dalam bentuk RREF.
Metode eliminasi Gauss-Jordan merupakan metode yang umum digunakan untuk menyelesaikan sistem persamaan linear karena relatif mudah diterapkan dan menghasilkan solusi yang akurat. Metode ini juga dapat digunakan untuk menentukan apakah sistem persamaan linear memiliki solusi tunggal, solusi tak hingga, atau tidak memiliki solusi.
Aplikasi Matriks
Matriks merupakan alat matematika yang sangat berguna dan memiliki aplikasi yang luas dalam berbagai bidang, mulai dari ilmu komputer hingga ekonomi. Aplikasi matriks dalam kehidupan nyata sangat penting karena memungkinkan kita untuk memodelkan dan memecahkan masalah kompleks dengan cara yang lebih efisien dan efektif.
Aplikasi Matriks dalam Kehidupan Nyata
Matriks memiliki aplikasi yang luas dalam berbagai bidang, termasuk:
- Ekonomi: Matriks digunakan untuk memodelkan dan menganalisis hubungan ekonomi, seperti permintaan dan penawaran, input dan output, serta pertumbuhan ekonomi. Contohnya, matriks input-output digunakan untuk menganalisis hubungan antar sektor dalam suatu ekonomi. Matriks juga digunakan dalam analisis portofolio untuk mengoptimalkan alokasi aset.
- Fisika: Matriks digunakan dalam mekanika kuantum, elektromagnetisme, dan teori relativitas. Misalnya, matriks digunakan untuk mewakili operator kuantum dalam mekanika kuantum, dan matriks rotasi digunakan untuk menggambarkan rotasi benda kaku dalam mekanika klasik.
- Informatika: Matriks digunakan dalam berbagai bidang informatika, termasuk pemrosesan gambar, komputasi grafis, dan pembelajaran mesin. Contohnya, matriks digunakan untuk menyimpan dan memanipulasi data gambar dalam pemrosesan gambar, dan matriks digunakan untuk mewakili data dalam algoritma pembelajaran mesin.
Contoh Aplikasi Matriks dalam Bidang Ekonomi
Berikut adalah tabel yang berisi contoh-contoh aplikasi matriks dalam bidang ekonomi:
| Aplikasi | Contoh |
|---|---|
| Analisis Portofolio | Matriks digunakan untuk mewakili portofolio investasi, dengan setiap baris mewakili aset dan setiap kolom mewakili karakteristik aset (misalnya, pengembalian, risiko). Matriks ini kemudian digunakan untuk mengoptimalkan alokasi aset berdasarkan tujuan investor. |
| Analisis Input-Output | Matriks input-output digunakan untuk menganalisis hubungan antar sektor dalam suatu ekonomi. Matriks ini menunjukkan berapa banyak input yang dibutuhkan dari setiap sektor untuk menghasilkan satu unit output di sektor lain. Matriks input-output digunakan untuk mengukur dampak perubahan dalam satu sektor terhadap sektor lain. |
Contoh Soal Aplikasi Matriks dalam Bidang Ekonomi
Sebuah perusahaan memiliki dua pabrik yang memproduksi dua jenis produk, yaitu A dan B. Pabrik 1 memproduksi 100 unit produk A dan 50 unit produk B per hari, sedangkan pabrik 2 memproduksi 75 unit produk A dan 100 unit produk B per hari. Jika harga jual produk A adalah Rp10.000 per unit dan harga jual produk B adalah Rp15.000 per unit, tentukan total pendapatan perusahaan per hari dengan menggunakan matriks.
Solusi:
Mari kita definisikan matriks produksi sebagai berikut:
“`
P = [100 50]
[75 100]
“`
Dimana baris pertama mewakili pabrik 1 dan baris kedua mewakili pabrik 2, sedangkan kolom pertama mewakili produk A dan kolom kedua mewakili produk B.
Mari kita definisikan matriks harga sebagai berikut:
“`
H = [10000]
[15000]
“`
Dimana baris pertama mewakili harga produk A dan baris kedua mewakili harga produk B.
Total pendapatan perusahaan per hari dapat dihitung dengan mengalikan matriks produksi dengan matriks harga:
“`
Total Pendapatan = P * H
“`
“`
Total Pendapatan = [100 50] * [10000]
[75 100] [15000]
“`
“`
Total Pendapatan = [100*10000 + 50*15000]
[75*10000 + 100*15000]
“`
“`
Total Pendapatan = [1750000]
[2250000]
“`
Jadi, total pendapatan perusahaan per hari adalah Rp1.750.000 dari pabrik 1 dan Rp2.250.000 dari pabrik 2, sehingga total pendapatan perusahaan per hari adalah Rp4.000.000.
Matriks dalam Transformasi Geometri
Matriks adalah alat yang sangat berguna dalam geometri, terutama dalam melakukan transformasi geometri. Transformasi geometri adalah perubahan posisi, ukuran, atau bentuk objek geometri. Matriks memungkinkan kita untuk merepresentasikan dan melakukan transformasi ini dengan cara yang sistematis dan efisien.
Cara Matriks Melakukan Transformasi Geometri
Matriks dapat digunakan untuk melakukan berbagai transformasi geometri, seperti rotasi, refleksi, dan translasi. Berikut penjelasan singkatnya:
- Rotasi: Rotasi adalah transformasi yang memutar objek di sekitar titik tetap yang disebut pusat rotasi. Matriks rotasi digunakan untuk menentukan sudut dan arah rotasi.
- Refleksi: Refleksi adalah transformasi yang mencerminkan objek melintasi garis atau bidang yang disebut sumbu refleksi. Matriks refleksi digunakan untuk menentukan sumbu refleksi.
- Translasi: Translasi adalah transformasi yang menggeser objek tanpa mengubah bentuk atau ukurannya. Matriks translasi digunakan untuk menentukan arah dan jarak perpindahan.
Menerapkan Matriks pada Titik atau Bangun Datar
Untuk melakukan transformasi geometri menggunakan matriks, kita perlu mengalikan matriks transformasi dengan matriks yang merepresentasikan titik atau bangun datar. Misalnya, untuk memutar titik (x, y) dengan sudut θ searah jarum jam, kita dapat menggunakan matriks rotasi berikut:
[cos(θ) -sin(θ)]
[sin(θ) cos(θ)]
Hasil perkalian matriks rotasi dengan matriks titik (x, y) akan menghasilkan titik baru yang merupakan hasil rotasi.
Contoh Soal Transformasi Geometri
Sebuah segitiga dengan titik-titik (1, 1), (2, 3), dan (4, 2) dirotasi 90 derajat searah jarum jam dengan pusat rotasi di titik asal (0, 0). Tentukan koordinat titik-titik segitiga setelah rotasi.
Penyelesaian:
1. Matriks rotasi untuk rotasi 90 derajat searah jarum jam adalah:
[0 -1]
[1 0]
2. Tulis titik-titik segitiga dalam bentuk matriks:
[1 2 4]
[1 3 2]
3. Kalikan matriks rotasi dengan matriks titik-titik segitiga:
[0 -1] [1 2 4] = [-1 -3 -2]
[1 0] [1 3 2] [1 2 4]
4. Jadi, koordinat titik-titik segitiga setelah rotasi adalah (-1, 1), (-3, 2), dan (-2, 4).
Matriks dalam Statistika
Matriks merupakan alat yang sangat berguna dalam statistika, khususnya dalam analisis data statistik. Matriks membantu dalam menyederhanakan dan mengatur data dalam bentuk yang terstruktur, sehingga memudahkan analisis dan interpretasi.
Penggunaan Matriks dalam Analisis Data Statistik
Matriks digunakan dalam analisis data statistik untuk berbagai tujuan, antara lain:
- Representasi Data: Matriks dapat digunakan untuk merepresentasikan data dalam bentuk tabel, dimana setiap baris mewakili observasi dan setiap kolom mewakili variabel. Hal ini memudahkan dalam melihat dan memahami hubungan antar variabel.
- Operasi Matematika: Operasi matematika seperti penjumlahan, pengurangan, perkalian, dan invers pada matriks dapat diterapkan pada data statistik. Operasi ini memungkinkan analisis yang lebih kompleks, seperti perhitungan korelasi dan regresi.
- Analisis Multivariat: Matriks merupakan alat yang penting dalam analisis multivariat, yaitu analisis yang melibatkan lebih dari satu variabel. Matriks memungkinkan kita untuk mengidentifikasi hubungan dan pola antar variabel, dan melakukan analisis faktor dan analisis klaster.
Contoh Soal tentang Korelasi Antar Variabel, Contoh soal tentang matriks
Misalkan kita memiliki data tentang tinggi badan dan berat badan dari 5 orang:
| Nama | Tinggi Badan (cm) | Berat Badan (kg) |
|---|---|---|
| A | 160 | 55 |
| B | 170 | 65 |
| C | 180 | 75 |
| D | 165 | 60 |
| E | 175 | 70 |
Data ini dapat direpresentasikan dalam bentuk matriks:
X =
⎡ 160 55 ⎤
⎢ 170 65 ⎥
⎢ 180 75 ⎥
⎢ 165 60 ⎥
⎣ 175 70 ⎦
Untuk menghitung korelasi antar variabel, kita dapat menggunakan rumus:
r = Cov(X,Y) / (SD(X) * SD(Y))
Dimana:
- r adalah koefisien korelasi
- Cov(X,Y) adalah kovariansi antara variabel X dan Y
- SD(X) dan SD(Y) adalah standar deviasi dari variabel X dan Y
Kovariansi dan standar deviasi dapat dihitung dengan menggunakan operasi matriks. Hasil perhitungan korelasi akan menunjukkan seberapa kuat hubungan antara tinggi badan dan berat badan.
Representasi Data dalam Analisis Multivariat
Dalam analisis multivariat, matriks digunakan untuk merepresentasikan data dalam bentuk yang terstruktur, seperti matriks kovariansi dan matriks korelasi. Matriks kovariansi menunjukkan variabilitas bersama antar variabel, sedangkan matriks korelasi menunjukkan hubungan linear antar variabel. Matriks ini membantu dalam memahami hubungan kompleks antar variabel dan melakukan analisis lebih lanjut.
Matriks dalam Komputer Grafis
Matriks merupakan alat yang sangat penting dalam komputer grafis, khususnya dalam manipulasi objek 3D. Mereka memungkinkan kita untuk melakukan transformasi seperti rotasi, translasi, dan scaling dengan cara yang efisien dan mudah dipahami.
Transformasi Objek 3D
Bayangkan sebuah objek 3D, seperti kubus atau bola. Untuk memindahkan, memutar, atau mengubah ukuran objek ini di ruang 3D, kita dapat menggunakan matriks. Setiap transformasi dapat direpresentasikan oleh sebuah matriks yang dikalikan dengan vektor yang merepresentasikan titik-titik objek.
- Translasi: Matriks translasi menggeser objek ke lokasi baru. Matriks ini akan menambahkan nilai tertentu ke koordinat x, y, dan z setiap titik pada objek.
- Rotasi: Matriks rotasi memutar objek di sekitar suatu sumbu. Matriks ini akan mengubah koordinat x, y, dan z setiap titik berdasarkan sudut rotasi.
- Scaling: Matriks scaling mengubah ukuran objek. Matriks ini akan mengalikan koordinat x, y, dan z setiap titik dengan faktor skala tertentu.
Contoh Soal: Animasi dan Rendering 3D
Bayangkan sebuah animasi 3D sederhana, seperti bola yang bergerak melengkung. Kita dapat menggunakan matriks untuk menghitung posisi bola pada setiap frame animasi.
Misalnya, untuk memindahkan bola dari titik (0, 0, 0) ke titik (10, 10, 10) dalam 10 frame, kita dapat menggunakan matriks translasi yang menambahkan 1 ke koordinat x, y, dan z setiap frame.
Pada setiap frame, matriks translasi dikalikan dengan vektor posisi bola untuk mendapatkan posisi baru bola.
Matriks Proyeksi
Matriks proyeksi digunakan untuk mengubah objek 3D ke dalam representasi 2D yang dapat ditampilkan pada layar.
Proses proyeksi ini memungkinkan kita untuk melihat objek 3D dari berbagai sudut pandang. Ada berbagai jenis proyeksi, seperti proyeksi perspektif dan proyeksi ortografik.
- Proyeksi Perspektif: Jenis proyeksi ini menciptakan efek kedalaman, di mana objek yang lebih jauh tampak lebih kecil. Ini adalah proyeksi yang paling sering digunakan dalam game dan film 3D.
- Proyeksi Ortografik: Jenis proyeksi ini tidak menciptakan efek kedalaman, di mana semua objek tampak dengan ukuran yang sama terlepas dari jaraknya. Ini sering digunakan dalam gambar teknik dan desain.
Matriks dalam Kriptografi
Matriks, dalam dunia matematika, adalah susunan angka yang disusun dalam baris dan kolom. Ternyata, susunan angka sederhana ini memiliki peran penting dalam keamanan data, khususnya dalam kriptografi. Kriptografi adalah ilmu tentang mengamankan informasi dengan mengubahnya menjadi bentuk yang tidak terbaca tanpa kunci khusus. Matriks berperan dalam enkripsi dan dekripsi pesan, mengubah pesan asli menjadi kode yang sulit dipahami dan kembali lagi ke bentuk aslinya.
Enkripsi dan Dekripsi dengan Matriks
Enkripsi dengan matriks melibatkan pengubahan pesan teks menjadi matriks angka, kemudian dikalikan dengan matriks kunci. Matriks kunci ini merupakan matriks khusus yang digunakan untuk mengenkripsi dan mendekripsi pesan. Hasil perkalian matriks menghasilkan matriks yang terenkripsi, yang kemudian diubah kembali menjadi teks terenkripsi. Proses dekripsi dilakukan dengan mengalikan matriks terenkripsi dengan invers matriks kunci. Invers matriks kunci merupakan matriks yang jika dikalikan dengan matriks kunci menghasilkan matriks identitas. Dengan demikian, pesan terenkripsi dapat diubah kembali menjadi pesan asli.
Contoh Soal
Misalkan kita ingin mengenkripsi pesan “HAI” dengan menggunakan matriks kunci:
K = [[1, 2], [3, 4]]
Langkah pertama adalah mengubah pesan “HAI” menjadi matriks angka, dengan menggunakan tabel alfabet sebagai panduan:
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
Maka, matriks pesan “HAI” adalah:
P = [[8, 1, 9]]
Selanjutnya, kita kalikan matriks pesan dengan matriks kunci:
C = P * K = [[8, 1, 9]] * [[1, 2], [3, 4]] = [[29, 42]]
Matriks C adalah matriks terenkripsi. Untuk mendekripsi pesan, kita perlu mencari invers matriks kunci, yaitu:
K-1 = [[-2, 1], [1.5, -0.5]]
Kemudian, kalikan matriks terenkripsi dengan invers matriks kunci:
P = C * K-1 = [[29, 42]] * [[-2, 1], [1.5, -0.5]] = [[8, 1, 9]]
Hasilnya adalah matriks pesan asli. Dengan mengubah kembali matriks angka ke teks, kita mendapatkan pesan “HAI” semula.
Matriks Kunci
Matriks kunci merupakan kunci rahasia dalam kriptografi matriks. Matriks ini harus dipilih dengan cermat agar sulit ditebak oleh pihak yang tidak berwenang. Berikut adalah beberapa aspek penting dalam memilih matriks kunci:
- Matriks kunci harus memiliki invers. Jika matriks kunci tidak memiliki invers, maka pesan yang terenkripsi tidak dapat didekripsi kembali.
- Matriks kunci harus cukup besar untuk membuat proses dekripsi menjadi rumit. Semakin besar matriks kunci, semakin sulit untuk menemukan inversnya.
- Matriks kunci harus dijaga kerahasiaannya. Jika matriks kunci diketahui oleh pihak yang tidak berwenang, maka pesan yang terenkripsi dapat didekripsi dengan mudah.
Penutupan
Dengan memahami konsep matriks, Anda membuka pintu menuju dunia matematika yang lebih luas dan kompleks. Matriks bukan hanya sekadar susunan bilangan, tetapi alat yang ampuh untuk memecahkan masalah dan memodelkan fenomena di berbagai bidang. Dari aplikasi praktis dalam kehidupan sehari-hari hingga kompleksitas dunia komputer, matriks memainkan peran penting dalam membentuk dunia kita.





