Contoh soal tentang vektor fisika kelas 10 – Vektor, konsep penting dalam fisika, hadir dalam berbagai aspek kehidupan kita. Dari arah dan kecepatan mobil hingga gaya yang kita gunakan untuk mendorong benda, vektor membantu kita memahami dunia secara lebih mendalam. Dalam fisika kelas 10, pemahaman tentang vektor menjadi dasar untuk mempelajari berbagai topik seperti gerak, gaya, dan energi.
Artikel ini akan mengajak Anda menjelajahi dunia vektor melalui contoh soal yang menarik dan menantang. Mulai dari pengertian dasar hingga penerapan vektor dalam berbagai fenomena fisika, Anda akan diajak untuk memahami konsep ini secara lebih komprehensif.
Pengertian Vektor
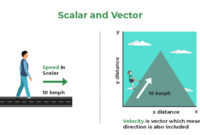
Dalam dunia fisika, kita seringkali berhadapan dengan besaran yang memiliki nilai dan arah. Besaran seperti ini disebut sebagai vektor. Vektor memiliki peran penting dalam memahami berbagai fenomena fisika, mulai dari gaya dan kecepatan hingga perpindahan dan medan magnet. Untuk memahami konsep vektor secara lebih mendalam, mari kita bahas pengertian vektor, contohnya dalam kehidupan sehari-hari, dan perbedaannya dengan besaran skalar.
Pengertian Vektor dalam Fisika
Vektor adalah besaran fisika yang memiliki nilai (besar) dan arah. Vektor dapat digambarkan sebagai panah dengan panjang tertentu yang mewakili nilai atau besarnya, dan arah panah menunjukkan arah vektor tersebut.
Contoh Vektor dalam Kehidupan Sehari-hari
Vektor hadir dalam berbagai aspek kehidupan kita. Berikut beberapa contohnya:
- Kecepatan mobil: Kecepatan mobil tidak hanya diukur dalam nilai (misalnya 60 km/jam) tetapi juga arah (misalnya ke timur).
- Gaya yang diberikan pada benda: Ketika kita mendorong atau menarik sebuah benda, gaya yang kita berikan memiliki nilai (besarnya gaya) dan arah (arah dorong atau tarikan).
- Perpindahan: Ketika kita berjalan dari satu titik ke titik lain, perpindahan kita memiliki nilai (jarak yang ditempuh) dan arah (arah perjalanan).
Perbedaan Vektor dan Skalar
Vektor dan skalar merupakan besaran fisika yang berbeda. Skalar adalah besaran yang hanya memiliki nilai, tanpa arah. Berikut perbedaannya:
| Ciri | Vektor | Skalar |
|---|---|---|
| Nilai | Memiliki nilai | Memiliki nilai |
| Arah | Memiliki arah | Tidak memiliki arah |
| Contoh | Kecepatan, gaya, perpindahan | Massa, suhu, waktu |
Penjumlahan dan Pengurangan Vektor
Vektor adalah besaran yang memiliki nilai dan arah. Dalam fisika, vektor digunakan untuk menggambarkan berbagai besaran seperti kecepatan, gaya, dan perpindahan. Penjumlahan dan pengurangan vektor adalah operasi dasar yang penting untuk memahami konsep vektor dan menerapkannya dalam berbagai masalah fisika.
Metode Penjumlahan Vektor Secara Grafis
Penjumlahan vektor secara grafis dapat dilakukan dengan menggunakan dua metode utama: metode segitiga dan metode jajargenjang. Metode ini membantu kita untuk memvisualisasikan penjumlahan vektor dan memahami arah resultan vektor.
Metode Segitiga
Metode segitiga adalah metode yang sederhana dan mudah dipahami. Dalam metode ini, dua vektor digambar sebagai sisi-sisi segitiga, dan resultan vektor merupakan sisi ketiga dari segitiga tersebut. Berikut adalah langkah-langkah penjumlahan vektor dengan metode segitiga:
- Gambarlah vektor pertama (A) dengan skala yang sesuai.
- Dari ujung vektor pertama (A), gambarlah vektor kedua (B) dengan skala yang sama dan sejajar dengan vektor kedua.
- Hubungkan titik awal vektor pertama (A) dengan ujung vektor kedua (B). Garis ini mewakili resultan vektor (R).
Arah resultan vektor (R) ditentukan oleh arah garis yang menghubungkan titik awal vektor pertama (A) dengan ujung vektor kedua (B). Besarnya resultan vektor (R) dapat diukur dengan menggunakan skala yang sama dengan yang digunakan untuk menggambar vektor pertama dan kedua.
Metode Jajargenjang
Metode jajargenjang adalah metode lain untuk menjumlahkan vektor secara grafis. Dalam metode ini, dua vektor digambar sebagai sisi-sisi jajargenjang, dan resultan vektor merupakan diagonal jajargenjang tersebut. Berikut adalah langkah-langkah penjumlahan vektor dengan metode jajargenjang:
- Gambarlah vektor pertama (A) dan vektor kedua (B) dengan skala yang sesuai.
- Dari titik ujung vektor pertama (A), gambarlah garis sejajar dengan vektor kedua (B) dengan panjang yang sama dengan vektor kedua.
- Dari titik ujung vektor kedua (B), gambarlah garis sejajar dengan vektor pertama (A) dengan panjang yang sama dengan vektor pertama.
- Hubungkan titik awal vektor pertama (A) dengan titik potong kedua garis yang baru dibuat. Garis ini mewakili resultan vektor (R).
Arah resultan vektor (R) ditentukan oleh arah garis yang menghubungkan titik awal vektor pertama (A) dengan titik potong kedua garis yang baru dibuat. Besarnya resultan vektor (R) dapat diukur dengan menggunakan skala yang sama dengan yang digunakan untuk menggambar vektor pertama dan kedua.
Metode Penjumlahan Vektor Secara Analitik
Metode penjumlahan vektor secara analitik menggunakan komponen-komponen vektor. Setiap vektor dapat diuraikan menjadi komponen-komponennya dalam sumbu x dan sumbu y. Penjumlahan vektor secara analitik dilakukan dengan menjumlahkan komponen-komponen yang searah.
Misalnya, vektor A dengan komponen Ax dan Ay, dan vektor B dengan komponen Bx dan By, maka resultan vektor (R) dapat dihitung dengan menggunakan rumus berikut:
Rx = Ax + Bx
Ry = Ay + By
Besarnya resultan vektor (R) dapat dihitung dengan menggunakan teorema Pythagoras:
R = √(Rx² + Ry²)
Arah resultan vektor (R) dapat dihitung dengan menggunakan rumus berikut:
θ = tan⁻¹(Ry/Rx)
di mana θ adalah sudut yang dibentuk oleh resultan vektor (R) dengan sumbu x.
Contoh Soal Pengurangan Vektor
Misalkan kita memiliki dua vektor, A dan B, dengan komponen-komponen sebagai berikut:
- A = (3, 4)
- B = (1, 2)
Untuk menghitung vektor A – B, kita dapat mengurangkan komponen-komponen yang searah:
A – B = (3 – 1, 4 – 2) = (2, 2)
Jadi, vektor A – B memiliki komponen (2, 2).
Perkalian Vektor dengan Skalar
Perkalian vektor dengan skalar merupakan operasi dasar dalam vektor yang melibatkan perkalian vektor dengan suatu bilangan. Hasil perkalian ini menghasilkan vektor baru yang memiliki arah yang sama atau berlawanan dengan vektor awal, tetapi dengan besar yang berbeda. Perkalian vektor dengan skalar memiliki banyak aplikasi dalam fisika, seperti dalam menghitung resultan gaya, kecepatan, dan percepatan.
Cara Mengalikan Vektor dengan Skalar
Untuk mengalikan vektor dengan skalar, cukup kalikan setiap komponen vektor dengan skalar tersebut. Misalkan kita memiliki vektor a = (ax, ay, az) dan skalar k, maka perkalian skalar dengan vektor tersebut dapat ditulis sebagai:
ka = (kax, kay, kaz)
Perkalian ini menghasilkan vektor baru yang memiliki arah yang sama atau berlawanan dengan vektor awal, tergantung pada tanda skalar k. Jika k positif, maka arah vektor baru sama dengan vektor awal. Jika k negatif, maka arah vektor baru berlawanan dengan vektor awal.
Contoh soal tentang vektor fisika kelas 10 biasanya membahas tentang penjumlahan, pengurangan, dan perkalian vektor, serta penerapannya dalam berbagai situasi. Konsep vektor ini juga memiliki peran penting dalam matematika terapan untuk bisnis dan ekonomi, seperti pada analisis data pasar, optimasi strategi produksi, dan perencanaan keuangan.
Sebagai contoh, untuk memahami bagaimana perubahan harga suatu produk memengaruhi permintaan, kita dapat menggunakan konsep vektor dan matriks. Nah, untuk mempelajari lebih lanjut tentang contoh soal matematika terapan untuk bisnis dan ekonomi, kamu bisa mengunjungi contoh soal matematika terapan untuk bisnis dan ekonomi.
Nah, kembali ke soal vektor fisika kelas 10, penting untuk memahami konsep-konsep dasar seperti resultan vektor dan proyeksi vektor agar kamu bisa menyelesaikan soal-soal yang lebih kompleks.
Contoh Soal Perkalian Vektor dengan Skalar
Misalkan kita memiliki vektor a = (2, 3, 1) dan skalar k = 3. Maka perkalian skalar dengan vektor tersebut adalah:
3a = 3(2, 3, 1) = (6, 9, 3)
Vektor baru 3a memiliki arah yang sama dengan vektor a, tetapi besarnya tiga kali lipat dari vektor a.
Pengaruh Perkalian Skalar terhadap Arah dan Besar Vektor
- Arah Vektor: Perkalian skalar dengan vektor tidak mengubah arah vektor jika skalarnya positif. Jika skalarnya negatif, arah vektor akan berlawanan dengan vektor awal.
- Besar Vektor: Perkalian skalar dengan vektor mengubah besar vektor. Besar vektor baru akan sama dengan besar vektor awal dikalikan dengan nilai absolut dari skalar.
Perkalian Vektor

Pada pembahasan sebelumnya, kita telah mengenal operasi penjumlahan dan pengurangan vektor. Dalam dunia fisika, operasi perkalian vektor juga sangat penting. Perkalian vektor memiliki dua jenis, yaitu perkalian dot (titik) dan perkalian silang. Kedua jenis perkalian ini memiliki perbedaan dalam cara menghitungnya dan hasil yang diperoleh.
Perkalian Dot (Titik) Vektor
Perkalian dot (titik) vektor adalah perkalian antara dua vektor yang menghasilkan skalar. Skalar adalah besaran yang hanya memiliki nilai dan tidak memiliki arah. Perkalian dot vektor sering digunakan untuk menentukan proyeksi satu vektor pada vektor lainnya, menghitung kerja yang dilakukan oleh gaya, atau menentukan besar sudut antara dua vektor.
Cara menghitung perkalian dot vektor adalah dengan mengalikan panjang proyeksi satu vektor pada vektor lainnya dengan panjang vektor yang lain. Secara matematis, perkalian dot vektor dapat dihitung dengan rumus:
A . B = |A| |B| cos θ
Dimana:
- A dan B adalah vektor.
- |A| dan |B| adalah besar vektor A dan B.
- θ adalah sudut antara vektor A dan B.
Contoh soal perkalian dot vektor:
Misalnya, terdapat dua vektor A dan B dengan besar |A| = 3 satuan dan |B| = 4 satuan. Sudut antara kedua vektor adalah 60 derajat. Hitunglah perkalian dot vektor A dan B!
Penyelesaian:
Pertama, kita cari cos 60 derajat yang nilainya 1/2. Kemudian, kita masukkan nilai ke dalam rumus:
A . B = |A| |B| cos θ = 3 x 4 x 1/2 = 6
Jadi, perkalian dot vektor A dan B adalah 6.
Perkalian Silang Vektor
Perkalian silang vektor adalah perkalian antara dua vektor yang menghasilkan vektor baru. Vektor baru ini tegak lurus terhadap kedua vektor awal dan arahnya ditentukan oleh aturan tangan kanan. Perkalian silang vektor sering digunakan untuk menghitung momen gaya, menghitung kecepatan sudut, atau menentukan arah medan magnet.
Cara menghitung perkalian silang vektor adalah dengan menggunakan rumus:
A x B = |A| |B| sin θ n
Dimana:
- A dan B adalah vektor.
- |A| dan |B| adalah besar vektor A dan B.
- θ adalah sudut antara vektor A dan B.
- n adalah vektor satuan yang tegak lurus terhadap vektor A dan B, arahnya ditentukan oleh aturan tangan kanan.
Contoh soal perkalian silang vektor:
Misalnya, terdapat dua vektor A dan B dengan besar |A| = 2 satuan dan |B| = 5 satuan. Sudut antara kedua vektor adalah 30 derajat. Hitunglah perkalian silang vektor A dan B!
Penyelesaian:
Pertama, kita cari sin 30 derajat yang nilainya 1/2. Kemudian, kita masukkan nilai ke dalam rumus:
A x B = |A| |B| sin θ n = 2 x 5 x 1/2 n = 5n
Jadi, perkalian silang vektor A dan B adalah 5n. Arah vektor n ditentukan oleh aturan tangan kanan, yaitu jika jari-jari tangan kanan menunjukkan arah vektor A dan jari tengah menunjukkan arah vektor B, maka ibu jari akan menunjukkan arah vektor n.
Proyeksi Vektor
Proyeksi vektor adalah konsep penting dalam fisika dan matematika yang digunakan untuk menentukan bagaimana suatu vektor diproyeksikan ke arah vektor lain. Dengan kata lain, proyeksi vektor adalah bayangan vektor pertama pada vektor kedua. Bayangan ini dapat berupa vektor atau skalar.
Pengertian Proyeksi Vektor
Proyeksi vektor merupakan representasi vektor yang diproyeksikan ke arah vektor lain. Vektor proyeksi ini adalah bayangan dari vektor pertama pada vektor kedua. Bayangan ini dapat berupa vektor atau skalar, tergantung pada jenis proyeksi yang dilakukan.
Contoh Soal Proyeksi Vektor, Contoh soal tentang vektor fisika kelas 10
Misalkan terdapat dua vektor, yaitu vektor a dan b. Vektor a = (3, 4) dan vektor b = (1, 2).
Untuk mencari proyeksi vektor a pada b, kita dapat menggunakan rumus:
Projba = ((a . b) / ||b||2) b
Dimana:
- a . b adalah hasil perkalian dot antara vektor a dan b.
- ||b|| adalah besarnya vektor b.
Langkah-langkah menghitung proyeksi vektor a pada b:
- Hitung perkalian dot antara a dan b:
a . b = (3 * 1) + (4 * 2) = 11 - Hitung besarnya vektor b:
||b|| = √(12 + 22) = √5 - Hitung proyeksi vektor a pada b:
Projba = ((11) / (√5)2) (1, 2) = (11/5, 22/5)
Jadi, proyeksi vektor a pada b adalah (11/5, 22/5).
Cara Menghitung Proyeksi Vektor
Ada beberapa cara untuk menghitung proyeksi vektor, tergantung pada jenis proyeksi yang ingin dicari:
- Proyeksi Skalar:
Proyeksi skalar adalah panjang proyeksi vektor pada vektor lain. Untuk menghitungnya, gunakan rumus:
Projba = (a . b) / ||b||
Rumus ini merupakan perkalian dot antara vektor a dan b, dibagi dengan besarnya vektor b.
- Proyeksi Vektor:
Proyeksi vektor adalah vektor yang dihasilkan dari proyeksi vektor pertama pada vektor kedua. Untuk menghitungnya, gunakan rumus:
Projba = ((a . b) / ||b||2) b
Rumus ini merupakan perkalian dot antara vektor a dan b, dibagi dengan kuadrat besarnya vektor b, lalu dikalikan dengan vektor b.
Vektor Posisi dan Perpindahan
Vektor posisi dan vektor perpindahan adalah konsep penting dalam fisika yang digunakan untuk menggambarkan lokasi dan perubahan posisi suatu objek. Kedua vektor ini memiliki arah dan besar, sehingga memberikan informasi lengkap tentang gerakan objek.
Vektor Posisi
Vektor posisi adalah vektor yang menunjukkan lokasi suatu objek terhadap titik acuan tertentu, yang biasanya disebut titik asal. Vektor posisi dilambangkan dengan simbol r dan digambarkan sebagai garis berarah yang menghubungkan titik asal ke lokasi objek.
Contoh Soal Vektor Posisi:
Sebuah mobil berada 5 km di sebelah timur dan 3 km di sebelah utara dari titik asal. Tentukan vektor posisi mobil tersebut!
- Vektor posisi mobil dapat diwakili oleh garis berarah yang menghubungkan titik asal ke lokasi mobil.
- Panjang vektor posisi adalah jarak antara titik asal dan lokasi mobil, yang dapat dihitung menggunakan teorema Pythagoras: √(5² + 3²) = √34 km.
- Arah vektor posisi dapat ditentukan dengan menggunakan sudut yang dibentuk oleh vektor posisi dengan sumbu x. Sudut tersebut dapat dihitung dengan menggunakan fungsi tangen: tan θ = 3/5, sehingga θ = 30,96°.
- Jadi, vektor posisi mobil adalah r = (5 km, 3 km) atau r = √34 km pada sudut 30,96° terhadap sumbu x.
Vektor Perpindahan
Vektor perpindahan adalah vektor yang menunjukkan perubahan posisi suatu objek dari posisi awal ke posisi akhir. Vektor perpindahan dilambangkan dengan simbol Δr dan digambarkan sebagai garis berarah yang menghubungkan posisi awal ke posisi akhir objek.
Contoh Soal Vektor Perpindahan:
Sebuah mobil bergerak dari titik A (2 km, 1 km) ke titik B (5 km, 4 km). Tentukan vektor perpindahan mobil tersebut!
- Vektor perpindahan mobil dapat diwakili oleh garis berarah yang menghubungkan titik A ke titik B.
- Panjang vektor perpindahan adalah jarak antara titik A dan titik B, yang dapat dihitung menggunakan teorema Pythagoras: √((5-2)² + (4-1)²) = √18 km.
- Arah vektor perpindahan dapat ditentukan dengan menggunakan sudut yang dibentuk oleh vektor perpindahan dengan sumbu x. Sudut tersebut dapat dihitung dengan menggunakan fungsi tangen: tan θ = (4-1)/(5-2) = 1, sehingga θ = 45°.
- Jadi, vektor perpindahan mobil adalah Δr = (3 km, 3 km) atau Δr = √18 km pada sudut 45° terhadap sumbu x.
Kecepatan dan Percepatan Vektor: Contoh Soal Tentang Vektor Fisika Kelas 10
Dalam fisika, kecepatan dan percepatan bukan hanya tentang seberapa cepat atau lambat suatu objek bergerak, tetapi juga tentang arah pergerakannya. Konsep ini diwakili oleh besaran vektor, yang memiliki besar dan arah. Kecepatan dan percepatan vektor berperan penting dalam memahami gerak benda, terutama dalam gerak lurus berubah beraturan (GLBB) dan gerak melingkar.
Kecepatan Vektor
Kecepatan vektor adalah besaran vektor yang menunjukkan seberapa cepat suatu objek bergerak dan ke arah mana objek tersebut bergerak. Kecepatan vektor dapat dihitung dengan membagi perpindahan dengan waktu tempuh. Perpindahan adalah perubahan posisi suatu objek dari posisi awal ke posisi akhir, dan merupakan besaran vektor.
- Rumus kecepatan vektor: v = Δr / Δt
- Dimana:
- v adalah kecepatan vektor
- Δr adalah perpindahan
- Δt adalah selang waktu
Contoh Soal Kecepatan Vektor
Sebuah mobil bergerak dari titik A ke titik B dengan kecepatan 72 km/jam ke arah timur. Kemudian, mobil tersebut berbelok ke arah utara dan bergerak dengan kecepatan 54 km/jam. Tentukan kecepatan vektor mobil tersebut!
- Kecepatan vektor mobil di awal: 72 km/jam ke arah timur
- Kecepatan vektor mobil setelah berbelok: 54 km/jam ke arah utara
- Kecepatan vektor total mobil: √(72² + 54²) = 90 km/jam
- Arah kecepatan vektor total: tan θ = 54/72 = 0,75, maka θ = 36,87° (sudut terhadap arah timur)
Jadi, kecepatan vektor total mobil adalah 90 km/jam dengan sudut 36,87° terhadap arah timur.
Percepatan Vektor
Percepatan vektor adalah besaran vektor yang menunjukkan seberapa cepat kecepatan suatu objek berubah dan ke arah mana perubahan kecepatan tersebut terjadi. Percepatan vektor dapat dihitung dengan membagi perubahan kecepatan dengan waktu tempuh. Perubahan kecepatan adalah selisih antara kecepatan akhir dan kecepatan awal suatu objek, dan merupakan besaran vektor.
- Rumus percepatan vektor: a = Δv / Δt
- Dimana:
- a adalah percepatan vektor
- Δv adalah perubahan kecepatan
- Δt adalah selang waktu
Contoh Soal Percepatan Vektor
Sebuah sepeda motor melaju dengan kecepatan 10 m/s ke arah timur. Kemudian, sepeda motor tersebut mengerem dan berhenti dalam waktu 5 detik. Tentukan percepatan vektor sepeda motor tersebut!
- Kecepatan awal sepeda motor: 10 m/s ke arah timur
- Kecepatan akhir sepeda motor: 0 m/s
- Perubahan kecepatan sepeda motor: Δv = 0 – 10 = -10 m/s
- Percepatan vektor sepeda motor: a = Δv / Δt = -10 / 5 = -2 m/s²
Jadi, percepatan vektor sepeda motor adalah -2 m/s² ke arah barat. Tanda negatif menunjukkan bahwa percepatan berlawanan arah dengan kecepatan awal.
Gaya dan Momentum Vektor
Dalam fisika, banyak besaran yang tidak hanya memiliki nilai numerik, tetapi juga arah. Besaran-besaran ini disebut besaran vektor. Gaya dan momentum adalah contoh besaran vektor yang penting dalam memahami pergerakan dan interaksi benda. Mari kita bahas lebih lanjut tentang gaya dan momentum vektor.
Pengertian Gaya Vektor
Gaya vektor adalah besaran yang memiliki nilai numerik dan arah. Nilai numerik gaya menunjukkan seberapa kuat gaya tersebut, sedangkan arahnya menunjukkan ke mana gaya tersebut bekerja. Gaya dapat menyebabkan perubahan kecepatan atau arah gerak benda.
Gaya vektor dapat digambarkan dengan panah. Panjang panah menunjukkan besarnya gaya, sedangkan arah panah menunjukkan arah gaya. Contohnya, jika kita mendorong sebuah kotak ke kanan dengan gaya 10 Newton, maka gaya vektor dapat digambarkan dengan panah yang panjangnya 10 unit dan mengarah ke kanan.
Contoh Soal Gaya Vektor
Sebuah kotak didorong oleh dua orang dengan gaya yang berbeda. Orang pertama mendorong kotak ke kanan dengan gaya 50 Newton, sedangkan orang kedua mendorong kotak ke kiri dengan gaya 30 Newton. Tentukan resultan gaya yang bekerja pada kotak tersebut.
Untuk menyelesaikan soal ini, kita dapat menggunakan prinsip penjumlahan vektor. Karena kedua gaya bekerja pada arah yang berlawanan, resultan gaya dapat dihitung dengan mengurangi kedua gaya tersebut. Jadi, resultan gaya yang bekerja pada kotak tersebut adalah 50 Newton – 30 Newton = 20 Newton ke kanan.
Pengertian Momentum Vektor
Momentum vektor adalah besaran yang mengukur kecenderungan suatu benda untuk mempertahankan gerak lurus beraturan. Momentum vektor merupakan hasil kali massa benda dengan kecepatannya. Momentum vektor juga memiliki nilai numerik dan arah.
Momentum vektor dapat digambarkan dengan panah. Panjang panah menunjukkan besarnya momentum, sedangkan arah panah menunjukkan arah gerak benda. Semakin besar massa benda atau kecepatannya, semakin besar momentumnya.
Contoh Soal Momentum Vektor
Sebuah mobil dengan massa 1000 kg bergerak dengan kecepatan 20 m/s ke timur. Tentukan momentum mobil tersebut.
Momentum mobil dapat dihitung dengan mengalikan massa mobil dengan kecepatannya. Jadi, momentum mobil tersebut adalah 1000 kg × 20 m/s = 20.000 kg m/s ke timur.
Penerapan Vektor dalam Fisika
Vektor adalah besaran fisika yang memiliki nilai dan arah. Dalam kehidupan sehari-hari, kita seringkali menjumpai besaran vektor seperti kecepatan, percepatan, gaya, dan perpindahan. Vektor memiliki peran penting dalam berbagai bidang fisika, mulai dari mekanika hingga elektromagnetisme.
Contoh Penerapan Vektor dalam Fisika
Berikut adalah beberapa contoh penerapan vektor dalam fisika:
- Kecepatan: Kecepatan adalah besaran vektor yang menunjukkan seberapa cepat suatu benda bergerak dan ke arah mana. Misalnya, mobil yang bergerak ke timur dengan kecepatan 60 km/jam memiliki kecepatan vektor yang berarah ke timur dan memiliki nilai 60 km/jam.
- Percepatan: Percepatan adalah besaran vektor yang menunjukkan seberapa cepat kecepatan suatu benda berubah dan ke arah mana. Misalnya, mobil yang melaju di jalan tol dengan kecepatan konstan memiliki percepatan nol, sementara mobil yang direm memiliki percepatan yang berarah berlawanan dengan arah gerak mobil.
- Gaya: Gaya adalah besaran vektor yang menunjukkan kekuatan yang bekerja pada suatu benda dan ke arah mana. Misalnya, gaya gravitasi yang bekerja pada apel yang jatuh dari pohon memiliki arah ke bawah dan memiliki nilai yang bergantung pada massa apel dan percepatan gravitasi.
- Perpindahan: Perpindahan adalah besaran vektor yang menunjukkan perubahan posisi suatu benda dari titik awal ke titik akhir. Misalnya, seorang pejalan kaki yang berjalan 5 meter ke utara kemudian 3 meter ke timur memiliki perpindahan vektor yang berarah ke arah timur laut dan memiliki nilai 5,83 meter (menggunakan teorema Pythagoras).
Tabel Penerapan Vektor dalam Fisika
Berikut adalah tabel yang berisi berbagai contoh penerapan vektor dalam fisika:
| Nama Penerapan | Deskripsi Singkat | Rumus yang Digunakan | Ilustrasi (Gambar) |
|---|---|---|---|
| Kecepatan | Besaran vektor yang menunjukkan seberapa cepat suatu benda bergerak dan ke arah mana. | v = Δs/Δt |
Ilustrasi: Sebuah mobil yang bergerak ke timur dengan kecepatan 60 km/jam. Vektor kecepatannya berarah ke timur dan memiliki nilai 60 km/jam. |
| Percepatan | Besaran vektor yang menunjukkan seberapa cepat kecepatan suatu benda berubah dan ke arah mana. | a = Δv/Δt |
Ilustrasi: Sebuah mobil yang direm memiliki percepatan yang berarah berlawanan dengan arah gerak mobil. |
| Gaya | Besaran vektor yang menunjukkan kekuatan yang bekerja pada suatu benda dan ke arah mana. | F = ma |
Ilustrasi: Gaya gravitasi yang bekerja pada apel yang jatuh dari pohon memiliki arah ke bawah dan memiliki nilai yang bergantung pada massa apel dan percepatan gravitasi. |
| Perpindahan | Besaran vektor yang menunjukkan perubahan posisi suatu benda dari titik awal ke titik akhir. | Δs = sakhir – sawal |
Ilustrasi: Seorang pejalan kaki yang berjalan 5 meter ke utara kemudian 3 meter ke timur memiliki perpindahan vektor yang berarah ke arah timur laut dan memiliki nilai 5,83 meter (menggunakan teorema Pythagoras). |
Contoh Kasus Nyata Penerapan Vektor dalam Fisika
Berikut adalah contoh kasus nyata penerapan vektor dalam fisika:
Sebuah pesawat terbang ingin terbang dari kota A ke kota B. Jarak antara kota A dan kota B adalah 500 km. Pesawat tersebut harus terbang dengan kecepatan 500 km/jam agar sampai di kota B dalam waktu 1 jam. Namun, angin bertiup dengan kecepatan 100 km/jam ke arah barat. Untuk mencapai kota B tepat waktu, pilot harus memperhitungkan arah dan kecepatan angin.
Pilot menggunakan vektor untuk menentukan arah dan kecepatan terbang yang tepat. Pilot harus terbang dengan kecepatan dan arah yang tepat agar pesawat dapat sampai di kota B tepat waktu, meskipun ada angin yang bertiup.
Soal Latihan Vektor
Vektor adalah besaran yang memiliki nilai dan arah. Vektor sangat penting dalam fisika, karena banyak besaran fisika yang bersifat vektor, seperti kecepatan, percepatan, gaya, dan momentum. Dalam mempelajari vektor, kamu akan mempelajari tentang penjumlahan vektor, pengurangan vektor, perkalian vektor dengan skalar, dan perkalian vektor dengan vektor lainnya.
Berikut ini adalah beberapa soal latihan tentang vektor yang bisa kamu kerjakan untuk menguji pemahamanmu tentang konsep vektor.
Soal Latihan Vektor
Soal latihan ini bertujuan untuk menguji pemahamanmu tentang operasi vektor dasar, seperti penjumlahan dan pengurangan vektor, serta perkalian vektor dengan skalar.
- Dua buah vektor, yaitu A = 3i + 4j dan B = -2i + 5j. Tentukan vektor resultan dari penjumlahan kedua vektor tersebut!
- Tentukan vektor satuan dari vektor A = 4i – 3j!
- Vektor A = 2i + 3j dan B = 4i – 2j. Tentukan hasil dari perkalian skalar 2 dengan vektor A + B!
- Tentukan sudut antara vektor A = 3i + 4j dan B = -2i + 5j!
- Dua buah vektor, yaitu A = 3i + 4j dan B = -2i + 5j. Tentukan proyeksi vektor A pada vektor B!
Solusi Soal Latihan Vektor
Berikut ini adalah solusi lengkap untuk setiap soal latihan vektor di atas.
-
Vektor resultan dari penjumlahan kedua vektor tersebut adalah:
A + B = (3i + 4j) + (-2i + 5j) = (3 – 2)i + (4 + 5)j = i + 9j
Jadi, vektor resultan dari penjumlahan kedua vektor tersebut adalah i + 9j.
-
Vektor satuan dari vektor A = 4i – 3j adalah:
 = A / |A| = (4i – 3j) / √(4² + (-3)²) = (4i – 3j) / 5 = (4/5)i – (3/5)j
Jadi, vektor satuan dari vektor A = 4i – 3j adalah (4/5)i – (3/5)j.
-
Hasil dari perkalian skalar 2 dengan vektor A + B adalah:
2(A + B) = 2[(2i + 3j) + (4i – 2j)] = 2(6i + j) = 12i + 2j
Jadi, hasil dari perkalian skalar 2 dengan vektor A + B adalah 12i + 2j.
-
Sudut antara vektor A = 3i + 4j dan B = -2i + 5j dapat ditentukan dengan menggunakan rumus:
cos θ = (A · B) / (|A| |B|)
Dimana A · B adalah perkalian dot antara vektor A dan B, |A| adalah panjang vektor A, dan |B| adalah panjang vektor B.
Pertama, kita hitung perkalian dot antara vektor A dan B:
A · B = (3i + 4j) · (-2i + 5j) = (3)(-2) + (4)(5) = 14
Kemudian, kita hitung panjang vektor A dan B:
|A| = √(3² + 4²) = 5
|B| = √((-2)² + 5²) = √29Sekarang, kita bisa menghitung sudut antara vektor A dan B:
cos θ = (A · B) / (|A| |B|) = 14 / (5 √29)
θ = arccos(14 / (5 √29)) ≈ 50.7°Jadi, sudut antara vektor A = 3i + 4j dan B = -2i + 5j adalah sekitar 50.7°.
-
Proyeksi vektor A pada vektor B dapat ditentukan dengan menggunakan rumus:
ProjBA = [(A · B) / (|B|²)] B
Dimana A · B adalah perkalian dot antara vektor A dan B, |B| adalah panjang vektor B.
Pertama, kita hitung perkalian dot antara vektor A dan B:
A · B = (3i + 4j) · (-2i + 5j) = (3)(-2) + (4)(5) = 14
Kemudian, kita hitung panjang vektor B:
|B| = √((-2)² + 5²) = √29
Sekarang, kita bisa menghitung proyeksi vektor A pada vektor B:
ProjBA = [(A · B) / (|B|²)] B = [14 / (√29)²] (-2i + 5j) = (14/29)(-2i + 5j) = (-28/29)i + (70/29)j
Jadi, proyeksi vektor A pada vektor B adalah (-28/29)i + (70/29)j.
Simpulan Akhir
Dengan memahami konsep vektor dan menguasai berbagai metode penyelesaian soal, Anda akan mampu menghadapi berbagai tantangan dalam mempelajari fisika. Melalui contoh soal yang disajikan, diharapkan Anda dapat mengasah kemampuan berpikir kritis dan analitis dalam menyelesaikan masalah yang berkaitan dengan vektor.