Contoh soal uji hipotesis 2 sampel – Uji hipotesis dua sampel merupakan teknik statistik yang digunakan untuk menguji perbedaan antara dua kelompok data. Teknik ini sering digunakan dalam berbagai bidang, seperti penelitian medis, ilmu sosial, dan bisnis, untuk menjawab pertanyaan seperti: “Apakah ada perbedaan signifikan dalam tingkat kepuasan pelanggan antara dua strategi pemasaran yang berbeda?” atau “Apakah ada perbedaan signifikan dalam skor ujian antara siswa yang menggunakan metode belajar A dan siswa yang menggunakan metode belajar B?”.
Artikel ini akan membahas contoh soal uji hipotesis dua sampel, mulai dari pengertian, jenis-jenis, langkah-langkah, interpretasi hasil, hingga aplikasi dalam berbagai bidang. Dengan memahami konsep dan penerapan uji hipotesis dua sampel, Anda dapat memperoleh pemahaman yang lebih baik tentang bagaimana menguji perbedaan antara dua kelompok data dan menarik kesimpulan yang valid berdasarkan data yang tersedia.
Pengertian Uji Hipotesis Dua Sampel: Contoh Soal Uji Hipotesis 2 Sampel
Uji hipotesis dua sampel adalah metode statistik yang digunakan untuk membandingkan dua kelompok data yang berbeda. Metode ini memungkinkan kita untuk menguji apakah terdapat perbedaan signifikan antara dua kelompok data tersebut, atau apakah perbedaan tersebut hanya terjadi karena faktor kebetulan.
Tujuan Uji Hipotesis Dua Sampel
Tujuan utama dari uji hipotesis dua sampel adalah untuk menentukan apakah terdapat perbedaan yang signifikan antara dua kelompok data yang berbeda. Dengan kata lain, kita ingin mengetahui apakah perbedaan yang kita amati antara kedua kelompok data tersebut merupakan hasil dari pengaruh variabel independen atau hanya terjadi secara kebetulan.
Jenis-Jenis Uji Hipotesis Dua Sampel
Ada berbagai jenis uji hipotesis dua sampel, yang pilihannya tergantung pada jenis data yang kita miliki dan tujuan penelitian kita. Beberapa jenis uji hipotesis dua sampel yang umum digunakan adalah:
- Uji t-dua sampel: Digunakan untuk membandingkan rata-rata dua kelompok data yang berdistribusi normal, dan asumsi varians sama.
- Uji z-dua sampel: Digunakan untuk membandingkan rata-rata dua kelompok data yang berdistribusi normal, dan asumsi varians tidak sama.
- Uji Mann-Whitney: Digunakan untuk membandingkan dua kelompok data yang tidak berdistribusi normal, dan asumsi varians tidak sama.
- Uji Wilcoxon: Digunakan untuk membandingkan dua kelompok data yang tidak berdistribusi normal, dan asumsi varians sama.
Asumsi yang Mendasari Uji Hipotesis Dua Sampel
Uji hipotesis dua sampel memiliki beberapa asumsi yang harus dipenuhi untuk memastikan hasil uji yang valid. Asumsi-asumsi ini bergantung pada jenis uji yang digunakan, namun secara umum meliputi:
- Data harus berdistribusi normal atau mendekati normal.
- Varians dari kedua kelompok data harus sama.
- Data harus independen, artinya data dari satu kelompok tidak dipengaruhi oleh data dari kelompok lain.
Jenis-Jenis Uji Hipotesis Dua Sampel
Uji hipotesis dua sampel adalah teknik statistik yang digunakan untuk membandingkan dua kelompok data dan menentukan apakah terdapat perbedaan signifikan antara keduanya. Jenis uji yang digunakan tergantung pada beberapa faktor, termasuk jenis data, ukuran sampel, dan hubungan antara kedua kelompok data.
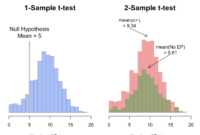
Perbedaan Uji t-test Dua Sampel dan Uji z-test Dua Sampel
Baik uji t-test dua sampel dan uji z-test dua sampel digunakan untuk membandingkan rata-rata dari dua kelompok data. Perbedaan utama antara keduanya terletak pada asumsi tentang populasi. Uji z-test mengasumsikan bahwa deviasi standar populasi diketahui, sedangkan uji t-test mengasumsikan bahwa deviasi standar populasi tidak diketahui.
- Uji z-test dua sampel digunakan ketika deviasi standar populasi diketahui, dan ukuran sampel cukup besar (biasanya lebih dari 30). Contohnya, jika kita ingin membandingkan rata-rata tinggi badan pria dan wanita di suatu negara, dan kita memiliki data dari sensus nasional yang memberikan deviasi standar tinggi badan untuk pria dan wanita, maka kita dapat menggunakan uji z-test.
- Uji t-test dua sampel digunakan ketika deviasi standar populasi tidak diketahui, dan ukuran sampel kecil (biasanya kurang dari 30). Contohnya, jika kita ingin membandingkan efektivitas dua jenis obat baru pada pasien dengan penyakit tertentu, dan kita hanya memiliki data dari sampel kecil pasien, maka kita dapat menggunakan uji t-test.
Perbedaan Uji Hipotesis Dua Sampel Independen dan Uji Hipotesis Dua Sampel Berpasangan
Uji hipotesis dua sampel independen digunakan untuk membandingkan dua kelompok data yang tidak terkait, sedangkan uji hipotesis dua sampel berpasangan digunakan untuk membandingkan dua kelompok data yang terkait.
- Uji hipotesis dua sampel independen digunakan ketika kedua kelompok data tidak saling berhubungan. Contohnya, jika kita ingin membandingkan skor ujian siswa yang belajar dengan metode A dan siswa yang belajar dengan metode B, dan kedua kelompok siswa tidak saling berhubungan, maka kita dapat menggunakan uji hipotesis dua sampel independen.
- Uji hipotesis dua sampel berpasangan digunakan ketika kedua kelompok data saling berhubungan. Contohnya, jika kita ingin membandingkan tekanan darah pasien sebelum dan sesudah mengonsumsi obat tertentu, dan data tekanan darah sebelum dan sesudah mengonsumsi obat merupakan data yang saling berhubungan, maka kita dapat menggunakan uji hipotesis dua sampel berpasangan.
Contoh Kasus untuk Setiap Jenis Uji Hipotesis Dua Sampel
- Uji t-test dua sampel independen: Membandingkan rata-rata tinggi badan siswa laki-laki dan perempuan di suatu sekolah. Asumsi: Deviasi standar tinggi badan siswa laki-laki dan perempuan tidak diketahui, dan kedua kelompok siswa tidak saling berhubungan.
- Uji t-test dua sampel berpasangan: Membandingkan skor ujian siswa sebelum dan sesudah mengikuti program pelatihan tertentu. Asumsi: Deviasi standar skor ujian sebelum dan sesudah pelatihan tidak diketahui, dan kedua kelompok skor ujian saling berhubungan.
- Uji z-test dua sampel independen: Membandingkan rata-rata pendapatan penduduk di kota A dan kota B. Asumsi: Deviasi standar pendapatan penduduk di kota A dan kota B diketahui, dan kedua kelompok penduduk tidak saling berhubungan.
- Uji z-test dua sampel berpasangan: Membandingkan tingkat kepuasan pelanggan sebelum dan sesudah implementasi program layanan pelanggan baru. Asumsi: Deviasi standar tingkat kepuasan pelanggan sebelum dan sesudah implementasi program diketahui, dan kedua kelompok data saling berhubungan.
Cara Memilih Jenis Uji Hipotesis Dua Sampel yang Tepat
Untuk memilih jenis uji hipotesis dua sampel yang tepat, perlu mempertimbangkan beberapa faktor, yaitu:
- Jenis data: Apakah data kontinu atau kategorikal?
- Ukuran sampel: Apakah ukuran sampel besar atau kecil?
- Hubungan antara kedua kelompok data: Apakah kedua kelompok data saling berhubungan atau tidak?
- Asumsi tentang populasi: Apakah deviasi standar populasi diketahui atau tidak?
Setelah mempertimbangkan faktor-faktor tersebut, dapat ditentukan jenis uji hipotesis dua sampel yang paling sesuai untuk kasus yang sedang dihadapi.
Langkah-Langkah Melakukan Uji Hipotesis Dua Sampel
Uji hipotesis dua sampel adalah teknik statistik yang digunakan untuk membandingkan dua kelompok data dan menentukan apakah ada perbedaan yang signifikan antara keduanya. Uji ini sering digunakan dalam berbagai bidang seperti ilmu sosial, kesehatan, dan bisnis untuk menguji hipotesis tentang perbedaan rata-rata, proporsi, atau varians antara dua kelompok.
Langkah-Langkah Melakukan Uji Hipotesis Dua Sampel
Berikut adalah langkah-langkah yang terlibat dalam melakukan uji hipotesis dua sampel:
- Rumuskan Hipotesis Nol dan Hipotesis Alternatif
- Tentukan Tingkat Signifikansi
- Pilih Statistik Uji yang Tepat
- Hitung Statistik Uji
- Tentukan Nilai-p
- Buat Keputusan
Rumuskan Hipotesis Nol dan Hipotesis Alternatif
Langkah pertama dalam melakukan uji hipotesis dua sampel adalah merumuskan hipotesis nol dan hipotesis alternatif. Hipotesis nol (H0) menyatakan bahwa tidak ada perbedaan yang signifikan antara dua kelompok, sedangkan hipotesis alternatif (H1) menyatakan bahwa ada perbedaan yang signifikan.
Contohnya, jika kita ingin menguji apakah ada perbedaan yang signifikan dalam tinggi badan antara pria dan wanita, hipotesis nol akan menyatakan bahwa tidak ada perbedaan yang signifikan dalam tinggi badan antara pria dan wanita, sedangkan hipotesis alternatif akan menyatakan bahwa ada perbedaan yang signifikan dalam tinggi badan antara pria dan wanita.
Tentukan Tingkat Signifikansi
Tingkat signifikansi (α) adalah probabilitas menolak hipotesis nol ketika sebenarnya benar. Tingkat signifikansi biasanya ditetapkan pada 0,05, yang berarti bahwa ada probabilitas 5% menolak hipotesis nol ketika sebenarnya benar.
Tingkat signifikansi menunjukkan seberapa yakin kita ingin menjadi dalam menolak hipotesis nol. Semakin rendah tingkat signifikansi, semakin yakin kita harus menjadi dalam menolak hipotesis nol.
Pilih Statistik Uji yang Tepat
Statistik uji yang digunakan dalam uji hipotesis dua sampel bergantung pada jenis data yang dikumpulkan dan hipotesis yang ingin diuji. Beberapa statistik uji yang umum digunakan termasuk:
- Uji t: Uji t digunakan untuk membandingkan rata-rata dua kelompok ketika data berdistribusi normal dan variansnya sama.
- Uji z: Uji z digunakan untuk membandingkan proporsi dua kelompok ketika ukuran sampel cukup besar.
- Uji F: Uji F digunakan untuk membandingkan varians dua kelompok.
Hitung Statistik Uji
Setelah memilih statistik uji yang tepat, langkah selanjutnya adalah menghitung statistik uji. Statistik uji adalah ukuran seberapa berbeda kedua kelompok. Statistik uji dihitung dengan menggunakan data sampel dan rumus yang sesuai dengan statistik uji yang dipilih.
Tentukan Nilai-p
Nilai-p adalah probabilitas mendapatkan hasil yang sama atau lebih ekstrem dari data sampel, dengan asumsi bahwa hipotesis nol benar. Nilai-p dihitung dengan menggunakan distribusi statistik uji.
Nilai-p menunjukkan seberapa kuat bukti yang mendukung hipotesis alternatif. Semakin rendah nilai-p, semakin kuat bukti yang mendukung hipotesis alternatif.
Buat Keputusan
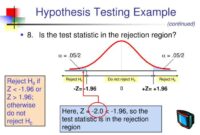
Langkah terakhir dalam melakukan uji hipotesis dua sampel adalah membuat keputusan. Keputusan dibuat dengan membandingkan nilai-p dengan tingkat signifikansi (α).
Jika nilai-p kurang dari tingkat signifikansi (α), maka hipotesis nol ditolak. Ini berarti bahwa ada bukti yang cukup untuk mendukung hipotesis alternatif.
Jika nilai-p lebih besar dari atau sama dengan tingkat signifikansi (α), maka hipotesis nol tidak ditolak. Ini berarti bahwa tidak ada bukti yang cukup untuk mendukung hipotesis alternatif.
Interpretasi Hasil Uji Hipotesis Dua Sampel
Setelah melakukan uji hipotesis dua sampel, langkah selanjutnya adalah menginterpretasikan hasil yang diperoleh. Interpretasi ini penting untuk menarik kesimpulan yang valid dan bermakna dari data yang dianalisis.
Cara Menginterpretasikan Hasil Uji Hipotesis Dua Sampel
Interpretasi hasil uji hipotesis dua sampel melibatkan beberapa aspek, termasuk:
- Nilai p-value: Nilai p-value menunjukkan probabilitas mendapatkan hasil yang diamati atau lebih ekstrem jika hipotesis nol benar. Nilai p-value yang kecil (biasanya kurang dari 0,05) menunjukkan bahwa hasil yang diamati tidak mungkin terjadi jika hipotesis nol benar, sehingga hipotesis nol ditolak.
- Statistik uji: Statistik uji merupakan ukuran perbedaan antara kedua sampel. Nilai statistik uji yang besar menunjukkan perbedaan yang signifikan antara kedua sampel.
- Interval kepercayaan: Interval kepercayaan merupakan rentang nilai yang diperkirakan berisi parameter populasi yang sebenarnya. Interval kepercayaan yang tidak berisi nilai hipotesis nol menunjukkan bahwa hipotesis nol ditolak.
Cara Menentukan Nilai p-value
Nilai p-value dapat ditentukan menggunakan perangkat lunak statistik seperti SPSS atau R. Perangkat lunak ini akan menghitung nilai p-value berdasarkan statistik uji yang diperoleh dan distribusi statistik uji yang sesuai. Nilai p-value dapat juga ditentukan menggunakan tabel distribusi statistik uji yang tersedia di buku teks statistik.
Cara Menentukan Kesimpulan Berdasarkan Nilai p-value
Kesimpulan uji hipotesis dua sampel ditentukan berdasarkan nilai p-value dan tingkat signifikansi (alpha). Tingkat signifikansi umumnya ditetapkan pada 0,05. Jika nilai p-value kurang dari tingkat signifikansi, maka hipotesis nol ditolak. Sebaliknya, jika nilai p-value lebih besar dari tingkat signifikansi, maka hipotesis nol tidak ditolak.
Cara Membuat Tabel Ringkasan Hasil Uji Hipotesis Dua Sampel
Tabel ringkasan hasil uji hipotesis dua sampel dapat membantu dalam menyajikan hasil uji secara terstruktur dan mudah dipahami. Tabel ini biasanya berisi informasi berikut:
| Variabel | Sampel 1 | Sampel 2 | Statistik Uji | Nilai p-value | Kesimpulan |
|---|---|---|---|---|---|
| Rata-rata | Nilai Rata-rata Sampel 1 | Nilai Rata-rata Sampel 2 | Nilai Statistik Uji | Nilai p-value | Kesimpulan |
Contoh: Misalkan kita ingin menguji apakah terdapat perbedaan signifikan dalam skor ujian matematika antara siswa yang mengikuti program bimbingan belajar dan siswa yang tidak mengikuti program bimbingan belajar. Hasil uji hipotesis dua sampel menunjukkan nilai p-value sebesar 0,02. Karena nilai p-value kurang dari tingkat signifikansi (0,05), maka hipotesis nol ditolak. Kesimpulannya, terdapat perbedaan signifikan dalam skor ujian matematika antara siswa yang mengikuti program bimbingan belajar dan siswa yang tidak mengikuti program bimbingan belajar.
Contoh soal uji hipotesis 2 sampel biasanya membahas perbandingan dua kelompok data. Misalnya, membandingkan rata-rata nilai ujian siswa di kelas A dan kelas B. Nah, untuk mempresentasikan hasil analisis ini, kamu bisa menggunakan media presentasi seperti PowerPoint. Latihan membuat presentasi bisa kamu temukan di contoh soal power point yang banyak tersedia online.
Setelah mempelajari materi dan latihan, kamu bisa mencoba membuat presentasi hasil analisis uji hipotesis 2 sampelmu sendiri.
Contoh Soal Uji Hipotesis Dua Sampel
Uji hipotesis dua sampel digunakan untuk membandingkan dua kelompok data yang berbeda. Tujuannya adalah untuk menentukan apakah ada perbedaan signifikan antara kedua kelompok tersebut. Contohnya, Anda mungkin ingin membandingkan rata-rata nilai ujian siswa yang menggunakan metode pembelajaran tradisional dengan rata-rata nilai ujian siswa yang menggunakan metode pembelajaran online.
Contoh Soal Uji Hipotesis Dua Sampel
Misalkan kita ingin mengetahui apakah ada perbedaan signifikan dalam tinggi badan antara siswa laki-laki dan perempuan di sebuah sekolah. Data tinggi badan (dalam cm) dari 10 siswa laki-laki dan 10 siswa perempuan diperoleh seperti berikut:
Data Tinggi Badan Siswa
| Laki-laki | Perempuan |
|---|---|
| 170 | 165 |
| 175 | 160 |
| 180 | 168 |
| 172 | 170 |
| 178 | 162 |
| 168 | 165 |
| 173 | 163 |
| 177 | 172 |
| 182 | 167 |
| 171 | 169 |
Langkah-langkah Penyelesaian Soal
Langkah-langkah untuk menyelesaikan soal uji hipotesis dua sampel adalah sebagai berikut:
- Merumuskan Hipotesis Nol (H0) dan Hipotesis Alternatif (H1)
- H0: Tidak ada perbedaan signifikan dalam tinggi badan antara siswa laki-laki dan perempuan. (μL = μP)
- H1: Ada perbedaan signifikan dalam tinggi badan antara siswa laki-laki dan perempuan. (μL ≠ μP)
- Menentukan Tingkat Signifikansi (α)
- Tingkat signifikansi biasanya ditetapkan sebesar 0,05, yang berarti bahwa kita bersedia menerima risiko 5% untuk menolak hipotesis nol jika hipotesis nol sebenarnya benar.
- Memilih Uji Statistik yang Tepat
- Dalam kasus ini, karena kita membandingkan rata-rata dua kelompok data yang independen, uji statistik yang tepat adalah uji t-dua sampel.
- Menghitung Statistik Uji
- Statistik uji dihitung dengan menggunakan rumus uji t-dua sampel.
- Menentukan Nilai-p
- Nilai-p adalah probabilitas mendapatkan hasil yang sama ekstrem atau lebih ekstrem daripada yang diamati, dengan asumsi hipotesis nol benar.
- Membuat Keputusan
- Jika nilai-p kurang dari tingkat signifikansi (α), maka kita menolak hipotesis nol.
- Jika nilai-p lebih besar dari atau sama dengan tingkat signifikansi (α), maka kita gagal menolak hipotesis nol.
- Menginterpretasikan Hasil
- Interpretasi hasil didasarkan pada keputusan yang dibuat dalam langkah sebelumnya.
Tabel Ringkasan Hasil Uji Hipotesis Dua Sampel
Hasil uji hipotesis dua sampel dapat diringkas dalam tabel seperti berikut:
| Hipotesis | Statistik Uji | Nilai-p | Keputusan | Interpretasi |
|---|---|---|---|---|
| H0: μL = μP | t = … | p = … | … | … |
Interpretasi Hasil Uji Hipotesis Dua Sampel
Interpretasi hasil uji hipotesis dua sampel didasarkan pada keputusan yang dibuat dalam langkah sebelumnya. Jika hipotesis nol ditolak, maka kita dapat menyimpulkan bahwa ada perbedaan signifikan dalam tinggi badan antara siswa laki-laki dan perempuan. Jika hipotesis nol gagal ditolak, maka kita tidak dapat menyimpulkan bahwa ada perbedaan signifikan dalam tinggi badan antara siswa laki-laki dan perempuan.
Aplikasi Uji Hipotesis Dua Sampel
Uji hipotesis dua sampel adalah teknik statistik yang digunakan untuk membandingkan dua kelompok data dan menentukan apakah ada perbedaan yang signifikan antara keduanya. Metode ini sangat berguna dalam berbagai bidang, mulai dari ilmu sosial hingga ilmu kesehatan, dan membantu peneliti dalam membuat kesimpulan yang bermakna tentang populasi yang diteliti.
Contoh Aplikasi Uji Hipotesis Dua Sampel dalam Berbagai Bidang
Uji hipotesis dua sampel memiliki aplikasi luas dalam berbagai bidang. Berikut adalah beberapa contoh:
- Ilmu Kesehatan: Membandingkan efektivitas dua jenis obat untuk mengobati penyakit tertentu. Misalnya, peneliti dapat menggunakan uji hipotesis dua sampel untuk membandingkan efektivitas obat A dan obat B dalam mengurangi tekanan darah pada pasien hipertensi.
- Ilmu Sosial: Membandingkan tingkat kepuasan pelanggan terhadap dua produk atau layanan yang berbeda. Misalnya, sebuah perusahaan dapat menggunakan uji hipotesis dua sampel untuk membandingkan tingkat kepuasan pelanggan terhadap produk A dan produk B, untuk menentukan produk mana yang lebih disukai oleh konsumen.
- Bisnis: Membandingkan kinerja penjualan dua strategi pemasaran yang berbeda. Misalnya, perusahaan dapat menggunakan uji hipotesis dua sampel untuk membandingkan kinerja penjualan kampanye pemasaran digital dan kampanye pemasaran tradisional, untuk menentukan strategi mana yang lebih efektif dalam meningkatkan penjualan.
- Pendidikan: Membandingkan efektivitas dua metode pembelajaran yang berbeda. Misalnya, seorang guru dapat menggunakan uji hipotesis dua sampel untuk membandingkan hasil belajar siswa yang mengikuti metode pembelajaran A dan metode pembelajaran B, untuk menentukan metode mana yang lebih efektif dalam meningkatkan pemahaman siswa.
Contoh Kasus Nyata yang Menggunakan Uji Hipotesis Dua Sampel
Sebagai contoh, sebuah perusahaan farmasi ingin menguji efektivitas obat baru untuk mengobati penyakit jantung. Mereka melakukan uji klinis dengan melibatkan dua kelompok pasien. Kelompok pertama diberi obat baru, sementara kelompok kedua diberi plasebo (obat tiruan). Setelah periode tertentu, peneliti mengukur tingkat penurunan kolesterol pada kedua kelompok. Mereka kemudian menggunakan uji hipotesis dua sampel untuk menentukan apakah ada perbedaan yang signifikan dalam penurunan kolesterol antara kedua kelompok. Jika hasil uji menunjukkan perbedaan yang signifikan, maka peneliti dapat menyimpulkan bahwa obat baru efektif dalam menurunkan kolesterol.
Manfaat dari Penerapan Uji Hipotesis Dua Sampel
Penerapan uji hipotesis dua sampel memiliki beberapa manfaat, antara lain:
- Membuat Kesimpulan yang Objektif: Uji hipotesis dua sampel membantu peneliti dalam membuat kesimpulan yang objektif dan terukur tentang perbedaan antara dua kelompok data.
- Menguji Hipotesis: Uji hipotesis dua sampel memungkinkan peneliti untuk menguji hipotesis yang diajukan tentang populasi yang diteliti.
- Membuat Keputusan yang Lebih Baik: Dengan menggunakan uji hipotesis dua sampel, peneliti dapat membuat keputusan yang lebih baik dan terinformasi berdasarkan data yang tersedia.
Keterbatasan dari Uji Hipotesis Dua Sampel
Meskipun bermanfaat, uji hipotesis dua sampel juga memiliki beberapa keterbatasan:
- Asumsi Data: Uji hipotesis dua sampel mengasumsikan bahwa data yang digunakan berasal dari distribusi normal. Jika data tidak normal, maka hasil uji dapat menjadi tidak akurat.
- Ukuran Sampel: Ukuran sampel yang kecil dapat memengaruhi hasil uji. Ukuran sampel yang terlalu kecil dapat menyebabkan hasil uji yang tidak akurat.
- Variabilitas Data: Variabilitas data yang tinggi dapat memengaruhi hasil uji. Variabilitas data yang tinggi dapat membuat sulit untuk membedakan perbedaan yang signifikan antara dua kelompok data.
Software untuk Melakukan Uji Hipotesis Dua Sampel

Dalam melakukan uji hipotesis dua sampel, penggunaan software statistik dapat mempermudah proses analisis data dan meningkatkan akurasi hasil. Software ini menawarkan berbagai fitur dan kemampuan yang membantu dalam menjalankan uji hipotesis, interpretasi hasil, dan visualisasi data.
Software untuk Uji Hipotesis Dua Sampel
Beberapa software yang umum digunakan untuk melakukan uji hipotesis dua sampel antara lain:
- SPSS (Statistical Package for the Social Sciences): Software statistik yang populer dan komprehensif yang menawarkan berbagai fitur untuk analisis data, termasuk uji hipotesis dua sampel. SPSS menyediakan antarmuka yang mudah digunakan dan berbagai pilihan uji statistik, seperti uji t, uji z, dan uji ANOVA.
- R: Bahasa pemrograman statistik yang open source dan kuat. R menawarkan fleksibilitas tinggi dalam analisis data dan memiliki paket-paket yang luas untuk melakukan uji hipotesis dua sampel. R sangat cocok untuk pengguna yang ingin memiliki kontrol penuh atas analisis mereka.
- Microsoft Excel: Software spreadsheet yang banyak digunakan, Excel juga dapat digunakan untuk melakukan uji hipotesis dua sampel. Meskipun tidak sekomprehensif SPSS atau R, Excel menawarkan fitur-fitur dasar untuk uji t dan uji z.
- JMP (Statistical Discovery): Software statistik interaktif yang menawarkan antarmuka yang ramah pengguna dan visualisasi data yang canggih. JMP memungkinkan pengguna untuk melakukan uji hipotesis dua sampel dengan mudah dan menginterpretasikan hasil dengan visualisasi yang menarik.
- Minitab: Software statistik yang mudah digunakan dan ditujukan untuk berbagai pengguna, termasuk pelajar dan profesional. Minitab menawarkan fitur-fitur untuk uji hipotesis dua sampel, analisis data, dan visualisasi.
Cara Melakukan Uji Hipotesis Dua Sampel
Langkah-langkah melakukan uji hipotesis dua sampel menggunakan software umumnya serupa, meskipun antarmuka dan fitur mungkin berbeda. Berikut adalah langkah-langkah umum yang dapat diterapkan pada berbagai software:
- Masuk ke software: Buka software statistik yang Anda pilih.
- Impor data: Impor data yang ingin Anda analisis ke dalam software. Data harus terstruktur dalam format yang sesuai dengan software.
- Pilih uji statistik: Pilih uji statistik yang sesuai dengan hipotesis Anda. Untuk uji hipotesis dua sampel, Anda mungkin memilih uji t, uji z, atau uji ANOVA.
- Tentukan variabel: Tentukan variabel independen dan variabel dependen yang akan Anda analisis. Variabel independen adalah variabel yang Anda manipulasi, sedangkan variabel dependen adalah variabel yang Anda ukur.
- Atur parameter: Atur parameter uji statistik, seperti tingkat signifikansi (alpha) dan hipotesis nol.
- Jalankan uji: Jalankan uji statistik dengan mengklik tombol “run” atau “execute” pada software.
- Interpretasi hasil: Analisis hasil uji statistik, termasuk nilai p, statistik uji, dan interval kepercayaan. Bandingkan nilai p dengan tingkat signifikansi untuk menentukan apakah Anda menolak atau gagal menolak hipotesis nol.
Perbedaan Antar Software
Perbedaan utama antar software terletak pada fitur, antarmuka, dan kemampuannya. Beberapa software lebih komprehensif dan menawarkan berbagai pilihan uji statistik, sedangkan yang lain lebih sederhana dan ditujukan untuk pengguna tertentu. Berikut adalah beberapa perbedaan utama:
- Antarmuka: SPSS dan JMP memiliki antarmuka yang lebih ramah pengguna, sedangkan R dan Minitab lebih berorientasi pada pemrograman.
- Fitur: SPSS menawarkan berbagai fitur untuk analisis data, termasuk uji hipotesis dua sampel, analisis regresi, dan analisis faktor. R memiliki paket-paket yang luas untuk berbagai analisis statistik, termasuk uji hipotesis dua sampel, analisis data spasial, dan analisis data time series.
- Harga: SPSS dan JMP merupakan software berbayar, sedangkan R dan Minitab memiliki versi gratis dan berbayar. Excel merupakan software yang sudah termasuk dalam paket Microsoft Office.
- Fleksibilitas: R menawarkan fleksibilitas tinggi dalam analisis data, memungkinkan pengguna untuk menyesuaikan kode dan analisis sesuai kebutuhan. SPSS dan JMP lebih berorientasi pada analisis statistik yang standar.
Contoh Screenshot
Berikut adalah contoh screenshot langkah-langkah melakukan uji hipotesis dua sampel menggunakan SPSS:
Contoh screenshot SPSS:
1. Impor data ke dalam SPSS.
2. Pilih menu “Analyze” > “Compare Means” > “Independent-Samples T Test”.
3. Tentukan variabel independen dan variabel dependen.
4. Atur parameter uji statistik, seperti tingkat signifikansi (alpha) dan hipotesis nol.
5. Klik “OK” untuk menjalankan uji.
6. Interpretasikan hasil uji statistik, termasuk nilai p, statistik uji, dan interval kepercayaan.
Screenshot yang menunjukkan langkah-langkah di atas dapat dilampirkan di sini. Namun, karena keterbatasan kemampuan saya untuk menampilkan gambar, saya tidak dapat menyertakannya. Anda dapat menemukan contoh screenshot yang lebih detail di manual SPSS atau tutorial online.
Kesalahan Umum dalam Melakukan Uji Hipotesis Dua Sampel
Uji hipotesis dua sampel merupakan teknik statistik yang digunakan untuk membandingkan dua kelompok data. Teknik ini banyak digunakan dalam berbagai bidang, seperti penelitian medis, bisnis, dan sosial. Meskipun uji hipotesis dua sampel relatif mudah dipahami, beberapa kesalahan umum sering terjadi yang dapat memengaruhi hasil dan interpretasi data.
Memilih Uji yang Salah
Salah satu kesalahan umum dalam uji hipotesis dua sampel adalah memilih uji yang salah. Terdapat berbagai jenis uji hipotesis dua sampel, seperti uji t, uji z, uji Wilcoxon, dan uji Mann-Whitney. Pemilihan uji yang tepat tergantung pada beberapa faktor, seperti jenis data, distribusi data, dan hipotesis yang ingin diuji.
- Jika data berdistribusi normal dan varians kedua kelompok sama, maka uji t dapat digunakan.
- Jika data berdistribusi normal dan varians kedua kelompok berbeda, maka uji t dengan derajat bebas yang disesuaikan dapat digunakan.
- Jika data tidak berdistribusi normal, maka uji non-parametrik seperti uji Wilcoxon atau uji Mann-Whitney dapat digunakan.
Memilih uji yang salah dapat menyebabkan kesimpulan yang salah. Misalnya, jika data tidak berdistribusi normal dan uji t digunakan, maka hasil uji mungkin tidak akurat.
Tidak Memeriksa Asumsi
Setiap uji statistik memiliki asumsi yang harus dipenuhi agar hasil uji valid. Asumsi yang umum untuk uji hipotesis dua sampel meliputi distribusi normal, varians sama, dan independensi data.
- Jika asumsi tidak terpenuhi, maka hasil uji mungkin tidak akurat. Misalnya, jika data tidak berdistribusi normal dan uji t digunakan, maka hasil uji mungkin tidak akurat.
- Memeriksa asumsi dapat dilakukan dengan menggunakan berbagai metode, seperti uji normalitas, uji homogenitas varians, dan uji independensi.
Interpretasi Hasil yang Salah
Interpretasi hasil uji hipotesis dua sampel juga penting. Kesalahan umum adalah menginterpretasikan nilai p sebagai probabilitas hipotesis nol benar. Nilai p adalah probabilitas mendapatkan hasil yang sama atau lebih ekstrem jika hipotesis nol benar.
- Jika nilai p lebih kecil dari tingkat signifikansi, maka hipotesis nol ditolak. Hal ini tidak berarti bahwa hipotesis alternatif benar, tetapi hanya bahwa tidak ada bukti yang cukup untuk mendukung hipotesis nol.
- Interpretasi hasil uji hipotesis dua sampel harus mempertimbangkan konteks penelitian, ukuran efek, dan signifikansi praktis.
Tidak Memperhatikan Ukuran Efek
Ukuran efek adalah ukuran kekuatan hubungan atau perbedaan antara dua kelompok.
- Meskipun hasil uji hipotesis dua sampel signifikan, ukuran efek mungkin kecil, yang menunjukkan bahwa perbedaan antara kedua kelompok tidak signifikan secara praktis.
- Ukuran efek membantu dalam menginterpretasikan hasil uji dan menentukan apakah perbedaan antara kedua kelompok signifikan secara praktis.
Contoh Kasus
Misalnya, sebuah perusahaan ingin menguji apakah ada perbedaan signifikan dalam kepuasan pelanggan antara dua produk yang berbeda. Mereka melakukan survei kepuasan pelanggan dan mengumpulkan data dari 100 pelanggan untuk setiap produk. Setelah melakukan uji hipotesis dua sampel, mereka menemukan bahwa nilai p lebih kecil dari tingkat signifikansi. Hal ini menunjukkan bahwa ada perbedaan signifikan dalam kepuasan pelanggan antara kedua produk. Namun, mereka juga menemukan bahwa ukuran efeknya kecil, yang menunjukkan bahwa perbedaan antara kedua produk tidak signifikan secara praktis.
Dalam kasus ini, meskipun hasil uji hipotesis dua sampel signifikan, perusahaan harus mempertimbangkan ukuran efek dan konteks penelitian sebelum mengambil kesimpulan. Mungkin saja perbedaan dalam kepuasan pelanggan tidak signifikan secara praktis, meskipun hasil uji signifikan secara statistik.
Pengembangan Lebih Lanjut Uji Hipotesis Dua Sampel
Uji hipotesis dua sampel adalah alat statistik yang kuat untuk membandingkan dua kelompok data. Dalam beberapa tahun terakhir, uji hipotesis dua sampel telah berkembang secara signifikan, dengan metode baru dan aplikasi baru yang muncul di berbagai bidang. Artikel ini akan membahas beberapa perkembangan terbaru dalam uji hipotesis dua sampel, metode baru yang digunakan, aplikasi dalam riset terkini, dan tantangan yang dihadapi di masa depan.
Metode Baru dalam Uji Hipotesis Dua Sampel
Metode baru dalam uji hipotesis dua sampel telah dikembangkan untuk mengatasi keterbatasan metode tradisional dan untuk menangani jenis data yang lebih kompleks. Beberapa metode baru ini meliputi:
- Uji Bootstrap: Metode ini menggunakan resampling data untuk membangun distribusi sampling statistik uji, memungkinkan untuk melakukan uji hipotesis tanpa asumsi distribusi data. Ini berguna untuk data yang tidak normal atau memiliki ukuran sampel kecil.
- Uji Permutasi: Metode ini menggunakan permutasi data untuk membangun distribusi sampling statistik uji, memungkinkan untuk melakukan uji hipotesis tanpa asumsi distribusi data. Ini berguna untuk data yang tidak normal atau memiliki ukuran sampel kecil.
- Uji Bayesian: Metode ini menggunakan pendekatan Bayesian untuk melakukan uji hipotesis, yang memungkinkan untuk mempertimbangkan informasi sebelumnya dan memperoleh distribusi posterior untuk statistik uji.
- Uji Non-Parametrik: Metode ini tidak bergantung pada asumsi distribusi data dan dapat digunakan untuk data yang tidak normal atau memiliki ukuran sampel kecil. Contohnya termasuk uji Mann-Whitney U dan uji Wilcoxon Signed-Rank.
Aplikasi Uji Hipotesis Dua Sampel dalam Riset Terkini
Uji hipotesis dua sampel telah diterapkan secara luas dalam berbagai bidang penelitian, termasuk:
- Ilmu Kedokteran: Untuk membandingkan efektivitas dua pengobatan berbeda, untuk mengevaluasi perbedaan dalam hasil pasien antara dua kelompok, atau untuk mengidentifikasi faktor risiko yang terkait dengan penyakit.
- Ilmu Sosial: Untuk membandingkan efektivitas dua program intervensi, untuk mengevaluasi perbedaan dalam perilaku antara dua kelompok, atau untuk mengidentifikasi faktor-faktor yang berkontribusi pada perbedaan dalam hasil sosial.
- Ilmu Ekonomi: Untuk membandingkan efektivitas dua kebijakan ekonomi, untuk mengevaluasi perbedaan dalam kinerja ekonomi antara dua negara, atau untuk mengidentifikasi faktor-faktor yang berkontribusi pada perbedaan dalam pertumbuhan ekonomi.
Tantangan dalam Melakukan Uji Hipotesis Dua Sampel di Masa Depan
Meskipun perkembangan terbaru dalam uji hipotesis dua sampel, ada beberapa tantangan yang dihadapi di masa depan:
- Data yang kompleks: Data yang dikumpulkan dalam penelitian seringkali kompleks dan memiliki struktur yang tidak biasa, seperti data longitudinal, data panel, atau data jaringan. Mengadaptasi uji hipotesis dua sampel untuk data yang kompleks ini merupakan tantangan yang signifikan.
- Ukuran sampel kecil: Dalam beberapa penelitian, ukuran sampel kecil dapat membatasi kekuatan uji hipotesis. Mengembangkan metode yang lebih sensitif untuk data dengan ukuran sampel kecil adalah tantangan penting.
- Interpretasi hasil: Interpretasi hasil uji hipotesis dua sampel dapat menjadi kompleks, terutama ketika ada banyak faktor yang berkontribusi pada perbedaan antara dua kelompok. Mengembangkan alat dan metode untuk interpretasi yang lebih akurat dan mudah dipahami sangat penting.
Contoh Kasus Uji Hipotesis Dua Sampel
Uji hipotesis dua sampel merupakan metode statistik yang digunakan untuk membandingkan dua kelompok data dan menentukan apakah ada perbedaan yang signifikan antara keduanya. Metode ini banyak diterapkan dalam berbagai bidang, seperti kesehatan, bisnis, dan ilmu sosial.
Contoh Kasus Nyata
Misalnya, kita ingin mengetahui apakah ada perbedaan yang signifikan dalam tingkat kepuasan pelanggan antara dua jenis layanan pelanggan yang ditawarkan oleh sebuah perusahaan. Kita dapat menggunakan uji hipotesis dua sampel untuk menguji hipotesis nol yang menyatakan bahwa tidak ada perbedaan dalam tingkat kepuasan pelanggan antara kedua jenis layanan tersebut.
Data dan Penerapan Uji Hipotesis
Berikut adalah tabel data yang digunakan dalam kasus ini:
| Jenis Layanan | Tingkat Kepuasan |
|---|---|
| Layanan A | 85, 80, 90, 75, 88, 92, 83, 78, 86, 89 |
| Layanan B | 78, 82, 86, 75, 80, 84, 77, 81, 83, 79 |
Uji hipotesis dua sampel diterapkan dengan membandingkan rata-rata tingkat kepuasan pelanggan untuk kedua jenis layanan. Kita dapat menggunakan uji t-dua sampel untuk menguji hipotesis nol. Uji ini akan menghasilkan nilai p, yang menunjukkan probabilitas mendapatkan hasil seperti yang kita amati jika tidak ada perbedaan yang signifikan antara kedua jenis layanan.
Interpretasi Hasil, Contoh soal uji hipotesis 2 sampel
Jika nilai p kurang dari tingkat signifikansi (biasanya 0,05), kita akan menolak hipotesis nol dan menyimpulkan bahwa ada perbedaan yang signifikan dalam tingkat kepuasan pelanggan antara kedua jenis layanan. Sebaliknya, jika nilai p lebih besar dari tingkat signifikansi, kita tidak dapat menolak hipotesis nol dan tidak dapat menyimpulkan bahwa ada perbedaan yang signifikan.
Pemungkas
Uji hipotesis dua sampel merupakan alat yang kuat untuk menguji perbedaan antara dua kelompok data. Dengan memahami konsep dan langkah-langkahnya, Anda dapat menganalisis data dengan lebih akurat dan menarik kesimpulan yang valid. Penerapan uji hipotesis dua sampel dalam berbagai bidang memberikan manfaat yang signifikan dalam pengambilan keputusan dan pengembangan pengetahuan.