Contoh soal vektor fisika kelas 10 – Vektor, sebuah konsep penting dalam fisika, memiliki peran krusial dalam memahami berbagai fenomena alam. Di kelas 10, kamu akan mulai mempelajari tentang besaran berarah ini, mulai dari pengertian hingga penerapannya dalam berbagai situasi. Bayangkan, bagaimana kamu bisa menghitung kecepatan dan arah pergerakan sebuah benda, atau bagaimana gaya bekerja pada suatu objek? Di sinilah vektor berperan penting, memberikan informasi lengkap tentang besaran dan arahnya. Yuk, kita selami dunia vektor dengan contoh-contoh soal yang menarik!
Dalam artikel ini, kita akan menjelajahi konsep dasar vektor, mulai dari penjumlahan, pengurangan, hingga perkaliannya. Kamu akan menemukan berbagai contoh soal yang akan membantu memahami aplikasi vektor dalam fisika, seperti pada analisis gerak lurus, gerak parabola, dan gaya. Siapkan dirimu untuk memahami konsep ini dengan lebih mendalam dan siapkan dirimu untuk menghadapi soal-soal yang menantang!
Pengertian Vektor
Dalam dunia fisika, kita seringkali berhadapan dengan besaran yang memiliki nilai dan arah. Besaran semacam ini dikenal sebagai vektor. Vektor berperan penting dalam memahami berbagai fenomena fisika, seperti gaya, kecepatan, percepatan, dan perpindahan. Untuk memahami konsep vektor dengan lebih baik, mari kita bedakan dengan besaran skalar.
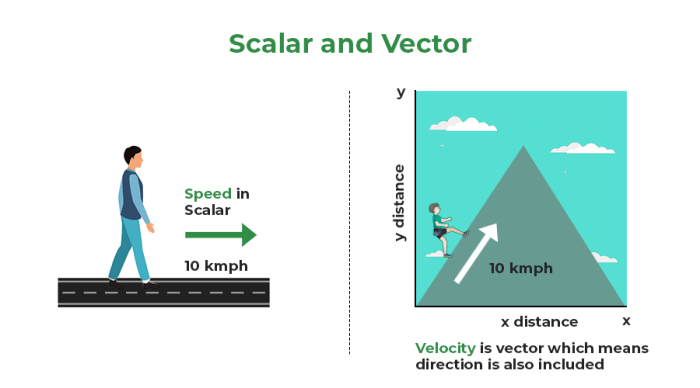
Perbedaan Vektor dan Skalar
Vektor dan skalar adalah dua jenis besaran yang berbeda dalam fisika. Berikut adalah perbedaannya:
- Vektor memiliki nilai dan arah. Contohnya, kecepatan 5 m/s ke timur adalah vektor, karena memiliki nilai 5 m/s dan arah ke timur.
- Skalar hanya memiliki nilai, tanpa arah. Contohnya, suhu 25 derajat Celcius adalah skalar, karena hanya memiliki nilai 25 derajat Celcius, tanpa arah.
Contoh Besaran Vektor dalam Kehidupan Sehari-hari
Besaran vektor banyak ditemukan dalam kehidupan sehari-hari. Berikut beberapa contohnya:
- Kecepatan mobil: Mobil yang bergerak dengan kecepatan 60 km/jam ke arah utara adalah vektor, karena memiliki nilai 60 km/jam dan arah ke utara.
- Gaya dorong: Gaya dorong yang diberikan pada sebuah kotak untuk menggerakkannya ke arah kanan adalah vektor, karena memiliki nilai dan arah tertentu.
- Perpindahan: Perpindahan seseorang dari titik A ke titik B adalah vektor, karena memiliki nilai dan arah tertentu.
Rumus Umum untuk Menghitung Besarnya Vektor
Besarnya vektor dapat dihitung menggunakan rumus Pythagoras. Misalkan vektor v memiliki komponen vx pada sumbu x dan vy pada sumbu y, maka besarnya vektor v dapat dihitung dengan:
|v| = √(vx2 + vy2)
Penjumlahan Vektor
Penjumlahan vektor adalah operasi matematika yang menggabungkan dua atau lebih vektor untuk menghasilkan vektor tunggal yang disebut resultan. Vektor adalah besaran yang memiliki nilai dan arah. Penjumlahan vektor dapat dilakukan secara grafis atau analitis.
Metode Penjumlahan Vektor Secara Grafis
Metode penjumlahan vektor secara grafis dapat dilakukan dengan menggunakan metode segitiga atau jajargenjang. Metode ini membantu memvisualisasikan bagaimana vektor-vektor digabungkan untuk menghasilkan resultan.
- Metode Segitiga
- Metode Jajargenjang
Metode segitiga melibatkan menggambar vektor pertama sebagai sisi pertama segitiga, lalu menggambar vektor kedua dengan titik awal pada ujung vektor pertama. Resultan adalah sisi ketiga segitiga yang menghubungkan titik awal vektor pertama dengan titik ujung vektor kedua.
Metode jajargenjang melibatkan menggambar vektor pertama dan kedua dengan titik awal yang sama. Kemudian, selesaikan jajargenjang dengan menggambar sisi sejajar dari kedua vektor. Resultan adalah diagonal jajargenjang yang dimulai dari titik awal kedua vektor.
Contoh Soal Penjumlahan Vektor Secara Grafis
Misalkan terdapat dua vektor, A dan B, dengan besar dan arah seperti yang ditunjukkan pada gambar berikut.
[Gambar ilustrasi dua vektor A dan B, yang digambar dengan sudut tertentu dan ditunjukkan panjangnya, kemudian resultan ditunjukkan sebagai vektor C, dengan deskripsi: Gambar ilustrasi dua vektor A dan B, dengan besar dan arah seperti yang ditunjukkan pada gambar berikut. Vektor A memiliki besar 5 satuan dan arah 30 derajat terhadap sumbu horizontal, sementara vektor B memiliki besar 3 satuan dan arah 60 derajat terhadap sumbu horizontal. Resultan dari kedua vektor tersebut adalah vektor C.]
Untuk mencari resultan dari kedua vektor tersebut, kita dapat menggunakan metode segitiga atau jajargenjang.
- Metode Segitiga
- Metode Jajargenjang
Gambar vektor A sebagai sisi pertama segitiga. Kemudian, gambar vektor B dengan titik awal pada ujung vektor A. Resultan, vektor C, adalah sisi ketiga segitiga yang menghubungkan titik awal vektor A dengan titik ujung vektor B.
Gambar vektor A dan B dengan titik awal yang sama. Kemudian, selesaikan jajargenjang dengan menggambar sisi sejajar dari kedua vektor. Resultan, vektor C, adalah diagonal jajargenjang yang dimulai dari titik awal kedua vektor.
Besar dan arah resultan vektor C dapat diukur secara langsung dari gambar. Dalam contoh ini, besar vektor C adalah sekitar 7 satuan dan arahnya adalah sekitar 45 derajat terhadap sumbu horizontal.
Metode Penjumlahan Vektor Secara Analitis
Metode penjumlahan vektor secara analitis menggunakan rumus untuk menghitung resultan vektor. Metode ini lebih akurat daripada metode grafis, terutama untuk vektor yang memiliki arah yang kompleks.
Jika vektor A dan B memiliki komponen-komponen x dan y sebagai berikut:
A = (Ax, Ay)
B = (Bx, By)
Maka, resultan vektor C dapat dihitung dengan rumus berikut:
C = (Ax + Bx, Ay + By)
Besar dan arah vektor C dapat dihitung dengan menggunakan teorema Pythagoras dan fungsi trigonometri.
Contoh soal penjumlahan vektor secara analitis:
Misalkan terdapat dua vektor, A dan B, dengan komponen-komponen sebagai berikut:
A = (3, 4)
B = (-2, 1)
Maka, resultan vektor C adalah:
C = (3 + (-2), 4 + 1) = (1, 5)
Besar vektor C adalah:
|C| = √(1² + 5²) = √26 ≈ 5.1 satuan
Arah vektor C adalah:
θ = tan⁻¹(5/1) ≈ 78.69 derajat terhadap sumbu horizontal
Pengurangan Vektor
Pengurangan vektor merupakan operasi yang melibatkan penggabungan dua vektor dengan memperhatikan arah dan besarnya. Dalam konteks ini, kita akan membahas metode pengurangan vektor secara grafis dan analitis. Metode grafis melibatkan representasi vektor dalam bentuk diagram, sedangkan metode analitis menggunakan rumus matematika.
Pengurangan Vektor Secara Grafis
Pengurangan vektor secara grafis dapat dilakukan dengan menggunakan dua metode, yaitu metode segitiga dan metode jajargenjang. Kedua metode ini memanfaatkan konsep penjumlahan vektor, karena pengurangan vektor dapat dianggap sebagai penjumlahan dengan vektor negatif.
- Metode Segitiga
- Metode Jajargenjang
Metode segitiga melibatkan penggambaran dua vektor secara berurutan, dengan ujung vektor pertama berimpit dengan pangkal vektor kedua. Vektor resultan, yang merupakan hasil pengurangan, diwakili oleh garis lurus yang menghubungkan pangkal vektor pertama dengan ujung vektor kedua. Vektor negatif dari vektor yang dikurangi di sini berperan sebagai vektor yang dijumlahkan.
Metode jajargenjang melibatkan penggambaran kedua vektor dengan pangkal yang berimpit. Kemudian, bentuk jajargenjang dibuat dengan menggambar garis sejajar dengan kedua vektor. Vektor resultan, yang merupakan hasil pengurangan, diwakili oleh garis lurus yang menghubungkan pangkal kedua vektor dengan titik pertemuan diagonal jajargenjang. Vektor negatif dari vektor yang dikurangi di sini berperan sebagai vektor yang dijumlahkan.
Contoh Soal Pengurangan Vektor Secara Grafis
Misalkan terdapat dua vektor, yaitu A dan B. Vektor A memiliki panjang 5 cm dan arah 30 derajat terhadap sumbu horizontal, sedangkan vektor B memiliki panjang 3 cm dan arah 60 derajat terhadap sumbu horizontal. Tentukan vektor resultan dari pengurangan vektor A dengan vektor B secara grafis dengan menggunakan metode segitiga dan jajargenjang.
Contoh soal vektor fisika kelas 10 biasanya melibatkan operasi penjumlahan, pengurangan, perkalian, dan pembagian vektor. Mengerjakan soal-soal tersebut mengharuskan pemahaman yang baik tentang konsep-konsep dasar vektor, seperti besar dan arah. Contoh soal pertidaksamaan rasional dan irasional, seperti yang dibahas dalam artikel ini , bisa membantu kamu melatih kemampuan dalam menyelesaikan persamaan dan pertidaksamaan, yang penting untuk memahami berbagai konsep fisika, termasuk vektor.
- Metode Segitiga
- Metode Jajargenjang
Gambarlah vektor A dan vektor B secara berurutan, dengan ujung vektor A berimpit dengan pangkal vektor B. Vektor negatif dari vektor B (yaitu -B) digambar dengan arah berlawanan dengan vektor B. Vektor resultan, yang merupakan hasil pengurangan A dengan B, diwakili oleh garis lurus yang menghubungkan pangkal vektor A dengan ujung vektor -B. Panjang dan arah vektor resultan dapat diukur dengan menggunakan penggaris dan busur derajat.
Gambarlah vektor A dan vektor B dengan pangkal yang berimpit. Kemudian, bentuk jajargenjang dibuat dengan menggambar garis sejajar dengan kedua vektor. Vektor resultan, yang merupakan hasil pengurangan A dengan B, diwakili oleh garis lurus yang menghubungkan pangkal kedua vektor dengan titik pertemuan diagonal jajargenjang. Panjang dan arah vektor resultan dapat diukur dengan menggunakan penggaris dan busur derajat.
Pengurangan Vektor Secara Analitis
Pengurangan vektor secara analitis dilakukan dengan menggunakan rumus resultan vektor. Vektor dapat diuraikan menjadi komponen-komponennya dalam arah sumbu x dan sumbu y. Komponen-komponen vektor tersebut kemudian dikurangkan secara terpisah, dan hasilnya dikombinasikan kembali untuk mendapatkan vektor resultan.
Rumus resultan vektor: R = (Rx, Ry) = (Ax – Bx, Ay – By)
di mana:
- R adalah vektor resultan
- Ax dan Ay adalah komponen vektor A pada sumbu x dan sumbu y
- Bx dan By adalah komponen vektor B pada sumbu x dan sumbu y
Perkalian Vektor dengan Skalar
Perkalian vektor dengan skalar adalah operasi matematika yang melibatkan perkalian vektor dengan sebuah bilangan skalar. Operasi ini menghasilkan vektor baru dengan arah yang sama atau berlawanan dengan vektor awal, dan besar yang dikalikan dengan skalar tersebut.
Konsep Perkalian Vektor dengan Skalar dan Contohnya
Misalnya, jika kita memiliki vektor a dengan besar 5 satuan dan arah ke kanan, dan kita mengalikannya dengan skalar 2, maka vektor baru yang dihasilkan, 2a, akan memiliki besar 10 satuan dan arah yang sama dengan a, yaitu ke kanan.
Jika kita mengalikan a dengan skalar -2, maka vektor baru, -2a, akan memiliki besar 10 satuan dan arah yang berlawanan dengan a, yaitu ke kiri.
Contoh Soal Perkalian Vektor dengan Skalar
Misalkan kita memiliki vektor v = (3, 4) dan skalar k = 2. Tentukan hasil perkalian kv.
Langkah-langkah Penyelesaian
- Kalikan setiap komponen vektor v dengan skalar k.
- Hasilnya adalah vektor baru kv = (2 * 3, 2 * 4) = (6, 8).
Pengaruh Perkalian Skalar Terhadap Arah dan Besar Vektor
| Skalar | Arah | Besar |
|---|---|---|
| Skalar positif | Sama dengan vektor awal | Dikali dengan skalar |
| Skalar negatif | Berlawanan dengan vektor awal | Dikali dengan nilai absolut skalar |
| Skalar nol | Tidak terdefinisi | Nol |
Perkalian Dot (Scalar)
Perkalian dot, juga dikenal sebagai perkalian skalar, adalah operasi pada dua vektor yang menghasilkan skalar. Skalar adalah besaran yang hanya memiliki nilai, tanpa arah. Perkalian dot memberikan informasi tentang bagaimana dua vektor saling terkait, khususnya mengenai proyeksi satu vektor pada yang lain.
Pengertian Perkalian Dot
Perkalian dot antara dua vektor a dan b didefinisikan sebagai hasil kali panjang proyeksi a pada b dengan panjang b. Secara matematis, perkalian dot dapat ditulis sebagai:
a . b = |a| |b| cos θ
di mana:
* a . b adalah perkalian dot antara vektor a dan b.
* |a| dan |b| adalah panjang vektor a dan b, masing-masing.
* θ adalah sudut antara vektor a dan b.
Contoh Soal Perkalian Dot
Soal:
Tentukan perkalian dot antara vektor a = (3, 4) dan b = (5, 12).
Penyelesaian:
1. Tentukan panjang vektor a dan b:
* |a| = √(3² + 4²) = 5
* |b| = √(5² + 12²) = 13
2. Hitung sudut antara vektor a dan b:
* cos θ = (a . b) / (|a| |b|)
* a . b = (3)(5) + (4)(12) = 63
* cos θ = 63 / (5 * 13) = 0.969
* θ = arccos(0.969) ≈ 14.04°
3. Hitung perkalian dot:
* a . b = |a| |b| cos θ
* a . b = 5 * 13 * cos 14.04° ≈ 63
Jadi, perkalian dot antara vektor a dan b adalah 63.
Perbedaan Perkalian Dot dan Perkalian Silang
| Fitur | Perkalian Dot | Perkalian Silang |
|—|—|—|
| Hasil | Skalar | Vektor |
| Definisi | Hasil kali panjang proyeksi satu vektor pada vektor lainnya dengan panjang vektor lainnya | Hasil kali panjang proyeksi satu vektor pada vektor lainnya dengan sinus sudut antara kedua vektor |
| Penerapan | Menentukan sudut antara dua vektor, menghitung kerja, menentukan proyeksi satu vektor pada vektor lainnya | Menentukan luas paralelogram yang dibentuk oleh dua vektor, menentukan arah gaya magnetik pada muatan yang bergerak dalam medan magnet |
| Sifat | Komutatif | Tidak komutatif |
Perkalian Silang (Vektor)
Perkalian silang adalah operasi vektor yang menghasilkan vektor baru yang tegak lurus terhadap kedua vektor awal. Vektor hasil ini memiliki besar yang sama dengan luas paralelogram yang dibentuk oleh kedua vektor awal. Perkalian silang ini sering digunakan dalam fisika untuk menghitung momen torsi, kecepatan sudut, dan gaya magnetik.
Pengertian Perkalian Silang
Perkalian silang antara dua vektor, a dan b, didefinisikan sebagai vektor c yang tegak lurus terhadap kedua vektor awal, dengan arah yang ditentukan oleh aturan tangan kanan. Arah vektor c ditentukan dengan cara:
- Telunjuk menunjukkan arah vektor a.
- Jari tengah menunjukkan arah vektor b.
- Ibu jari menunjukkan arah vektor c.
Besar vektor c dihitung dengan rumus:
|c| = |a| |b| sin θ
di mana θ adalah sudut antara vektor a dan b.
Contoh Soal Perkalian Silang
Misalkan kita memiliki dua vektor:
a = (2, 1, 3) dan b = (1, 4, -2)
Untuk menghitung perkalian silang antara a dan b, kita dapat menggunakan rumus berikut:
a x b = (aybz – azby, azbx – axbz, axby – aybx)
Dengan mensubstitusikan nilai-nilai dari vektor a dan b, kita mendapatkan:
a x b = ((1)(-2) – (3)(4), (3)(1) – (2)(-2), (2)(4) – (1)(1))
a x b = (-14, 7, 7)
Jadi, perkalian silang antara vektor a dan b adalah vektor (-14, 7, 7).
Arah Vektor Hasil Perkalian Silang
Arah vektor hasil perkalian silang dapat ditentukan berdasarkan arah kedua vektor awal. Berikut tabel yang menunjukkan arah vektor hasil perkalian silang berdasarkan arah kedua vektor awal:
| Arah Vektor a | Arah Vektor b | Arah Vektor c (a x b) |
|---|---|---|
| Sumbu x positif | Sumbu y positif | Sumbu z positif |
| Sumbu x positif | Sumbu y negatif | Sumbu z negatif |
| Sumbu x negatif | Sumbu y positif | Sumbu z negatif |
| Sumbu x negatif | Sumbu y negatif | Sumbu z positif |
| Sumbu y positif | Sumbu z positif | Sumbu x positif |
| Sumbu y positif | Sumbu z negatif | Sumbu x negatif |
| Sumbu y negatif | Sumbu z positif | Sumbu x negatif |
| Sumbu y negatif | Sumbu z negatif | Sumbu x positif |
| Sumbu z positif | Sumbu x positif | Sumbu y positif |
| Sumbu z positif | Sumbu x negatif | Sumbu y negatif |
| Sumbu z negatif | Sumbu x positif | Sumbu y negatif |
| Sumbu z negatif | Sumbu x negatif | Sumbu y positif |
Penerapan Vektor dalam Fisika
Vektor adalah besaran fisika yang memiliki nilai dan arah. Konsep vektor sangat penting dalam fisika karena memungkinkan kita untuk menganalisis dan memahami gerakan objek secara lebih detail. Vektor digunakan untuk mewakili berbagai besaran fisika seperti kecepatan, percepatan, gaya, dan perpindahan. Penerapan vektor dalam fisika sangat luas, dan di sini kita akan membahas bagaimana vektor diterapkan dalam analisis gerak lurus dan gerak parabola.
Penerapan Vektor dalam Analisis Gerak Lurus
Dalam analisis gerak lurus, vektor digunakan untuk menggambarkan perpindahan, kecepatan, dan percepatan benda. Perpindahan adalah perubahan posisi benda dari posisi awal ke posisi akhir. Kecepatan adalah laju perubahan perpindahan terhadap waktu, sedangkan percepatan adalah laju perubahan kecepatan terhadap waktu.
- Perpindahan: Perpindahan adalah vektor yang menunjukkan perubahan posisi suatu benda dari titik awal ke titik akhir. Misalnya, jika suatu benda bergerak 5 meter ke timur, perpindahannya adalah 5 meter ke timur.
- Kecepatan: Kecepatan adalah vektor yang menunjukkan laju perubahan posisi suatu benda terhadap waktu. Misalnya, jika suatu benda bergerak dengan kecepatan 10 meter per detik ke timur, kecepatannya adalah 10 meter per detik ke timur.
- Percepatan: Percepatan adalah vektor yang menunjukkan laju perubahan kecepatan suatu benda terhadap waktu. Misalnya, jika suatu benda bergerak dengan percepatan 2 meter per detik kuadrat ke timur, percepatannya adalah 2 meter per detik kuadrat ke timur.
Penerapan Vektor dalam Analisis Gerak Parabola, Contoh soal vektor fisika kelas 10
Gerak parabola adalah gerak benda yang bergerak dalam lintasan berbentuk parabola. Gerak parabola merupakan kombinasi dari gerak lurus beraturan pada arah horizontal dan gerak lurus berubah beraturan pada arah vertikal. Vektor digunakan untuk menganalisis komponen horizontal dan vertikal dari kecepatan dan percepatan benda yang bergerak parabola.
- Kecepatan: Kecepatan benda yang bergerak parabola dapat diuraikan menjadi dua komponen, yaitu kecepatan horizontal dan kecepatan vertikal. Kecepatan horizontal konstan karena tidak ada gaya yang bekerja pada arah horizontal, sedangkan kecepatan vertikal berubah karena pengaruh gaya gravitasi.
- Percepatan: Percepatan benda yang bergerak parabola hanya bekerja pada arah vertikal, yaitu percepatan gravitasi (g). Percepatan gravitasi ini menyebabkan kecepatan vertikal benda berubah secara konstan.
Contoh Soal Penerapan Vektor dalam Analisis Gerak Lurus
Sebuah mobil bergerak ke timur dengan kecepatan 20 meter per detik. Setelah 5 detik, mobil tersebut berbelok ke utara dengan kecepatan 15 meter per detik. Tentukan:
- Perpindahan mobil selama 5 detik pertama.
- Kecepatan rata-rata mobil selama 10 detik.
Penyelesaian:
- Perpindahan mobil selama 5 detik pertama adalah 20 meter per detik x 5 detik = 100 meter ke timur.
- Kecepatan rata-rata mobil selama 10 detik adalah (100 meter ke timur + 15 meter per detik x 5 detik ke utara) / 10 detik = 17,5 meter per detik ke arah timur laut.
Contoh Soal Penerapan Vektor dalam Analisis Gerak Parabola
Sebuah bola dilempar dengan kecepatan awal 20 meter per detik dengan sudut elevasi 30 derajat terhadap horizontal. Tentukan:
- Kecepatan horizontal dan vertikal bola saat dilempar.
- Jarak horizontal yang ditempuh bola sebelum mencapai titik tertinggi.
Penyelesaian:
- Kecepatan horizontal bola adalah 20 meter per detik x cos 30 derajat = 17,32 meter per detik. Kecepatan vertikal bola adalah 20 meter per detik x sin 30 derajat = 10 meter per detik.
- Jarak horizontal yang ditempuh bola sebelum mencapai titik tertinggi dapat dihitung dengan menggunakan persamaan:
Jarak horizontal = (kecepatan horizontal x waktu)
Waktu yang dibutuhkan bola untuk mencapai titik tertinggi dapat dihitung dengan menggunakan persamaan:
Waktu = kecepatan vertikal / percepatan gravitasi
Dengan mengganti nilai yang diketahui, maka jarak horizontal yang ditempuh bola sebelum mencapai titik tertinggi adalah 17,32 meter per detik x 1 detik = 17,32 meter.
Analisis Gaya pada Benda yang Bergerak pada Bidang Miring
Ketika sebuah benda berada pada bidang miring, gaya-gaya yang bekerja pada benda tersebut adalah gaya gravitasi, gaya normal, dan gaya gesekan.
| Gaya | Arah | Keterangan |
|---|---|---|
| Gaya gravitasi (Fg) | Vertikal ke bawah | Gaya yang menarik benda ke arah pusat bumi. |
| Gaya normal (Fn) | Tegak lurus permukaan bidang miring | Gaya yang diberikan oleh permukaan bidang miring pada benda, mencegah benda menembus permukaan. |
| Gaya gesekan (Ff) | Berlawanan arah dengan gerak benda | Gaya yang melawan gerak benda akibat kontak antara benda dan permukaan bidang miring. |
Gaya gravitasi dapat diuraikan menjadi dua komponen: komponen sejajar bidang miring (Fg//) dan komponen tegak lurus bidang miring (Fg⊥). Komponen Fg// menyebabkan benda bergerak ke bawah pada bidang miring, sedangkan komponen Fg⊥ diimbangi oleh gaya normal. Gaya gesekan bekerja berlawanan arah dengan gerak benda.
Vektor digunakan untuk menganalisis gaya-gaya yang bekerja pada benda yang bergerak pada bidang miring. Dengan menggunakan vektor, kita dapat menentukan resultan gaya yang bekerja pada benda, dan kemudian menghitung percepatan benda.
Vektor Posisi dan Perpindahan
Dalam fisika, vektor adalah besaran yang memiliki nilai dan arah. Vektor posisi dan vektor perpindahan adalah dua jenis vektor yang penting untuk memahami gerak suatu benda. Vektor posisi menunjukkan letak suatu benda relatif terhadap titik acuan tertentu, sedangkan vektor perpindahan menunjukkan perubahan posisi benda dari titik awal ke titik akhir. Perbedaan keduanya terletak pada titik acuannya, yaitu posisi awal dan titik akhir.
Pengertian Vektor Posisi dan Vektor Perpindahan
Vektor posisi adalah vektor yang menunjukkan letak suatu benda relatif terhadap titik acuan tertentu. Titik acuan ini dapat berupa titik asal koordinat atau titik referensi lainnya. Vektor posisi dilambangkan dengan simbol r.
Vektor perpindahan adalah vektor yang menunjukkan perubahan posisi suatu benda dari titik awal ke titik akhir. Vektor perpindahan dilambangkan dengan simbol Δr. Perhatikan bahwa vektor perpindahan hanya bergantung pada posisi awal dan akhir, tidak peduli lintasan yang ditempuh benda.
Contoh Soal Vektor Posisi dan Vektor Perpindahan
Misalnya, sebuah mobil bergerak dari titik A ke titik B seperti pada gambar berikut.
Titik A sebagai titik awal, dan titik B sebagai titik akhir.
Vektor posisi mobil di titik A adalah rA dan vektor posisi mobil di titik B adalah rB. Vektor perpindahan mobil dari titik A ke titik B adalah Δr.
Δr = rB – rA
Untuk menghitung vektor perpindahan, kita dapat menggunakan rumus berikut:
Δr = (xB – xA)i + (yB – yA)j
di mana:
- xA dan yA adalah koordinat titik A
- xB dan yB adalah koordinat titik B
- i dan j adalah vektor satuan pada sumbu x dan y
Misalnya, jika koordinat titik A adalah (2, 3) dan koordinat titik B adalah (5, 7), maka vektor perpindahan mobil adalah:
Δr = (5 – 2)i + (7 – 3)j = 3i + 4j
Vektor perpindahan ini menunjukkan bahwa mobil berpindah sejauh 3 satuan ke kanan dan 4 satuan ke atas.
Diagram Vektor Posisi dan Vektor Perpindahan
Diagram berikut menunjukkan vektor posisi dan vektor perpindahan mobil yang bergerak dari titik A ke titik B:
Gambar menunjukkan titik A dan titik B, dengan vektor posisi rA dan rB yang masing-masing menunjuk dari titik asal ke titik A dan titik B. Vektor perpindahan Δr digambar sebagai garis lurus yang menghubungkan titik A ke titik B.
Diagram ini menunjukkan bahwa vektor perpindahan adalah vektor yang menghubungkan titik awal dan titik akhir gerak, tidak peduli lintasan yang ditempuh benda.
Vektor Kecepatan dan Percepatan: Contoh Soal Vektor Fisika Kelas 10
Dalam dunia fisika, gerak benda tidak hanya ditentukan oleh seberapa cepat benda tersebut bergerak, tetapi juga ke arah mana benda tersebut bergerak. Untuk menggambarkan gerak benda yang memiliki arah, kita menggunakan konsep vektor. Vektor kecepatan dan vektor percepatan adalah dua contoh penting dari konsep vektor dalam fisika yang akan kita bahas lebih lanjut.
Pengertian Vektor Kecepatan dan Vektor Percepatan
Vektor kecepatan adalah besaran vektor yang menggambarkan seberapa cepat suatu benda bergerak dan ke arah mana benda tersebut bergerak. Vektor kecepatan memiliki besar (nilai) yang disebut kelajuan dan arah yang menunjukkan arah gerak benda. Contohnya, jika sebuah mobil bergerak ke timur dengan kecepatan 60 km/jam, maka vektor kecepatannya memiliki besar 60 km/jam dan arah ke timur.
Vektor percepatan adalah besaran vektor yang menggambarkan seberapa cepat perubahan kecepatan suatu benda. Vektor percepatan memiliki besar (nilai) yang menunjukkan seberapa cepat kecepatan berubah dan arah yang menunjukkan arah perubahan kecepatan. Contohnya, jika sebuah mobil yang bergerak ke timur dengan kecepatan 60 km/jam memperlambat lajunya hingga 40 km/jam dalam waktu 10 detik, maka vektor percepatannya memiliki besar 2 m/s² dan arah ke barat (berlawanan dengan arah gerak mobil).
Contoh Soal Vektor Kecepatan dan Vektor Percepatan
Sebuah mobil bergerak ke utara dengan kecepatan 20 m/s. Kemudian, mobil tersebut berbelok ke timur dan bergerak dengan kecepatan 30 m/s. Hitunglah besar dan arah vektor kecepatan akhir mobil tersebut!
Untuk menyelesaikan soal ini, kita dapat menggunakan konsep vektor dan teorema Pythagoras. Berikut langkah-langkah penyelesaiannya:
- Gambarlah diagram vektor kecepatan awal (ke utara) dan vektor kecepatan akhir (ke timur). Kedua vektor ini membentuk sudut siku-siku.
- Gunakan teorema Pythagoras untuk menghitung besar vektor kecepatan akhir (hipotenusa segitiga).
√(20² + 30²) = √1300 ≈ 36,06 m/s
- Hitung sudut antara vektor kecepatan akhir dan arah utara menggunakan fungsi trigonometri tangen (tan).
tan θ = (30 m/s) / (20 m/s) = 1,5
Maka, θ = tan⁻¹(1,5) ≈ 56,31°
- Jadi, besar vektor kecepatan akhir mobil adalah sekitar 36,06 m/s dan arahnya adalah 56,31° timur laut (diukur dari arah utara).
Diagram Vektor Kecepatan dan Vektor Percepatan
Berikut adalah diagram yang menunjukkan vektor kecepatan dan vektor percepatan suatu benda yang bergerak dengan kecepatan konstan dan dengan percepatan konstan:
Gerak dengan Kecepatan Konstan:
Dalam gerak dengan kecepatan konstan, vektor kecepatan memiliki besar yang tetap dan arah yang tetap. Vektor percepatannya adalah nol karena tidak ada perubahan kecepatan. Pada diagram, vektor kecepatan diwakili oleh garis panah merah yang memiliki panjang yang sama dan arah yang sama di setiap titik waktu. Vektor percepatan diwakili oleh garis panah biru yang berukuran nol karena tidak ada perubahan kecepatan.
Gerak dengan Percepatan Konstan:
Dalam gerak dengan percepatan konstan, vektor kecepatan memiliki besar yang berubah secara konstan dan arah yang tetap atau berubah secara konstan. Vektor percepatan memiliki besar yang tetap dan arah yang tetap. Pada diagram, vektor kecepatan diwakili oleh garis panah merah yang panjangnya berubah secara konstan dan arahnya tetap atau berubah secara konstan. Vektor percepatan diwakili oleh garis panah biru yang memiliki panjang yang sama dan arah yang sama di setiap titik waktu.
Vektor Gaya dan Momentum
Vektor gaya dan vektor momentum merupakan konsep penting dalam fisika yang berkaitan dengan gerak benda. Vektor gaya menggambarkan besar dan arah gaya yang bekerja pada benda, sementara vektor momentum menggambarkan besar dan arah gerak benda. Kedua vektor ini saling terkait dan berperan penting dalam memahami dinamika benda.
Pengertian Vektor Gaya dan Vektor Momentum
Vektor gaya adalah besaran vektor yang menggambarkan besar dan arah gaya yang bekerja pada suatu benda. Gaya dapat menyebabkan benda bergerak, berhenti, atau mengubah arah geraknya. Vektor gaya dilambangkan dengan F dan memiliki satuan Newton (N).
Vektor momentum adalah besaran vektor yang menggambarkan besar dan arah gerak suatu benda. Momentum suatu benda bergantung pada massa dan kecepatannya. Vektor momentum dilambangkan dengan p dan memiliki satuan kilogram meter per detik (kg m/s).
Contoh Soal Vektor Gaya dan Vektor Momentum
Sebuah mobil bermassa 1000 kg bergerak dengan kecepatan 20 m/s ke arah timur. Mobil tersebut kemudian direm hingga berhenti dalam waktu 5 detik.
a. Tentukan besar dan arah vektor gaya yang bekerja pada mobil selama pengereman.
b. Tentukan besar dan arah vektor momentum mobil sebelum dan sesudah pengereman.
Langkah-langkah penyelesaian:
a. Menentukan besar dan arah vektor gaya:
* Langkah 1: Hitung perubahan kecepatan mobil.
> Perubahan kecepatan = Kecepatan akhir – Kecepatan awal = 0 m/s – 20 m/s = -20 m/s.
* Langkah 2: Hitung percepatan mobil.
> Percepatan = Perubahan kecepatan / Waktu = -20 m/s / 5 s = -4 m/s².
* Langkah 3: Hitung besar gaya yang bekerja pada mobil.
> Gaya = Massa x Percepatan = 1000 kg x -4 m/s² = -4000 N.
* Langkah 4: Tentukan arah gaya.
> Karena percepatan bernilai negatif, maka arah gaya berlawanan dengan arah gerak mobil, yaitu ke arah barat.
b. Menentukan besar dan arah vektor momentum:
* Langkah 1: Hitung besar momentum mobil sebelum pengereman.
> Momentum = Massa x Kecepatan = 1000 kg x 20 m/s = 20000 kg m/s.
* Langkah 2: Tentukan arah momentum mobil sebelum pengereman.
> Arah momentum sama dengan arah kecepatan mobil, yaitu ke arah timur.
* Langkah 3: Hitung besar momentum mobil sesudah pengereman.
> Momentum = Massa x Kecepatan = 1000 kg x 0 m/s = 0 kg m/s.
* Langkah 4: Tentukan arah momentum mobil sesudah pengereman.
> Momentum mobil sesudah pengereman adalah nol, karena mobil telah berhenti.
Diagram Vektor Gaya dan Momentum
Berikut diagram yang menunjukkan vektor gaya yang bekerja pada mobil dan vektor momentum mobil tersebut:
[Gambar diagram vektor gaya dan momentum]
Diagram ini menunjukkan bahwa vektor gaya yang bekerja pada mobil berlawanan arah dengan vektor momentum mobil sebelum pengereman. Hal ini menyebabkan perubahan momentum mobil, yang mengakibatkan mobil berhenti.
Ulasan Penutup
Memahami vektor adalah kunci untuk membuka pintu menuju pemahaman fisika yang lebih dalam. Melalui contoh soal yang disajikan, kamu dapat melihat bagaimana vektor berperan penting dalam menyelesaikan berbagai masalah fisika. Ingat, memahami konsep vektor tidak hanya tentang menghafal rumus, tetapi juga tentang memahami bagaimana vektor bekerja dalam berbagai situasi. Jadi, jangan ragu untuk terus berlatih dan memperdalam pemahamanmu tentang konsep ini!