Mengerti matematika bukan hanya soal menghafal rumus, tetapi juga tentang kemampuan memecahkan masalah. Indikator pemecahan masalah matematika menjadi kunci untuk mengukur kemampuan berpikir kritis dan logis dalam menyelesaikan soal-soal matematika. Indikator ini memberikan gambaran jelas tentang bagaimana seseorang mendekati masalah, menganalisis informasi, dan menemukan solusi yang tepat.
Bayangkan seperti seorang detektif yang berusaha mengungkap kasus rumit. Mereka harus menganalisis bukti, mencari pola, dan menguji hipotesis untuk menemukan jawaban. Begitu pula dalam pemecahan masalah matematika, kita perlu memahami konsep, memilih strategi yang tepat, dan mengevaluasi hasil akhir. Indikator ini membantu kita memahami langkah-langkah yang diperlukan untuk menjadi ‘detektif’ yang handal dalam dunia matematika.
Pengertian Indikator Pemecahan Masalah Matematika
Indikator pemecahan masalah matematika adalah acuan atau patokan yang digunakan untuk mengukur kemampuan siswa dalam menyelesaikan masalah matematika. Indikator ini penting karena membantu guru dalam menilai sejauh mana siswa memahami konsep matematika dan menerapkannya dalam situasi nyata.
Pengertian Indikator Pemecahan Masalah Matematika
Indikator pemecahan masalah matematika adalah tolak ukur yang digunakan untuk menilai kemampuan siswa dalam memahami, menganalisis, dan menyelesaikan masalah matematika. Indikator ini mengacu pada langkah-langkah atau kriteria yang menunjukkan bahwa siswa telah berhasil menyelesaikan masalah matematika dengan tepat dan efektif.
Contoh Indikator Pemecahan Masalah Matematika
Berikut ini contoh indikator pemecahan masalah matematika dalam konteks pembelajaran:
- Siswa dapat mengidentifikasi informasi yang relevan dalam soal cerita matematika.
- Siswa dapat memilih strategi yang tepat untuk menyelesaikan masalah matematika.
- Siswa dapat menjelaskan langkah-langkah penyelesaian masalah matematika dengan jelas dan logis.
- Siswa dapat memeriksa kembali hasil penyelesaian masalah matematika.
Daftar Indikator Pemecahan Masalah Matematika
Berikut ini daftar indikator pemecahan masalah matematika beserta deskripsi singkatnya:
| Indikator | Deskripsi |
|---|---|
| Memahami masalah | Siswa dapat mengidentifikasi informasi yang relevan dalam soal cerita matematika, memahami konteks masalah, dan menentukan tujuan yang ingin dicapai. |
| Merencanakan strategi | Siswa dapat memilih strategi yang tepat untuk menyelesaikan masalah matematika, seperti menggunakan rumus, membuat diagram, atau melakukan percobaan. |
| Melaksanakan strategi | Siswa dapat menerapkan strategi yang dipilih dengan benar dan akurat, melakukan perhitungan yang tepat, dan menggunakan simbol matematika yang sesuai. |
| Memeriksa kembali hasil | Siswa dapat memeriksa kembali hasil penyelesaian masalah matematika, memastikan bahwa jawabannya masuk akal dan sesuai dengan konteks masalah. |
Tahapan Pemecahan Masalah Matematika
Pemecahan masalah matematika merupakan proses yang sistematis dan terstruktur. Dalam memecahkan masalah matematika, kita tidak hanya perlu memahami konsep dan rumus, tetapi juga mampu mengidentifikasi pola, menganalisis informasi, dan mengaplikasikan strategi yang tepat. Proses ini dapat dipecah menjadi beberapa tahapan yang saling terkait dan berurutan.
Tahapan Umum dalam Pemecahan Masalah Matematika
Secara umum, pemecahan masalah matematika melibatkan beberapa tahapan yang saling melengkapi, yang meliputi:
- Memahami Masalah: Tahap ini sangat penting untuk memastikan kita benar-benar mengerti apa yang diminta dalam soal. Hal ini melibatkan membaca soal dengan cermat, mengidentifikasi informasi yang diketahui dan yang ingin dicari, serta menentukan apa yang menjadi tujuan akhir dari soal.
- Merencanakan Strategi: Setelah memahami masalah, kita perlu merencanakan strategi yang akan digunakan untuk menyelesaikannya. Tahap ini melibatkan pemilihan konsep, rumus, atau teknik yang relevan dengan masalah yang dihadapi. Kita juga perlu memikirkan langkah-langkah yang akan dilakukan untuk mencapai solusi.
- Melaksanakan Strategi: Tahap ini merupakan tahap di mana kita menerapkan strategi yang telah direncanakan. Kita melakukan perhitungan, manipulasi aljabar, atau penggambaran diagram sesuai dengan strategi yang dipilih. Penting untuk melakukan setiap langkah dengan teliti dan hati-hati.
- Memeriksa Solusi: Setelah mendapatkan solusi, kita perlu memeriksa apakah solusi tersebut masuk akal dan benar. Kita dapat melakukan hal ini dengan menguji kembali solusi yang diperoleh dengan memasukkannya ke dalam soal awal, atau dengan melihat apakah solusi tersebut sesuai dengan konteks masalah.
Contoh Konkret Pemecahan Masalah Matematika
Untuk memperjelas tahapan-tahapan tersebut, mari kita lihat contoh berikut:
Sebuah toko kue menjual 2 jenis kue: kue coklat dan kue vanila. Pada hari Sabtu, toko tersebut menjual 120 kue coklat dan 80 kue vanila. Jika harga kue coklat Rp 10.000 dan harga kue vanila Rp 8.000, berapa total pendapatan toko kue tersebut pada hari Sabtu?
| Tahapan | Penjelasan | Contoh |
|---|---|---|
| Memahami Masalah | Kita perlu memahami informasi yang diberikan dan apa yang ingin dicari. | Kita tahu jumlah kue coklat dan vanila yang terjual, serta harga masing-masing jenis kue. Kita ingin mencari total pendapatan toko. |
| Merencanakan Strategi | Kita perlu menentukan langkah-langkah yang akan digunakan untuk menghitung total pendapatan. | Kita dapat menghitung pendapatan dari penjualan kue coklat dengan mengalikan jumlah kue coklat dengan harga per kue. Kemudian, kita dapat menghitung pendapatan dari penjualan kue vanila dengan cara yang sama. Terakhir, kita menjumlahkan kedua pendapatan tersebut untuk mendapatkan total pendapatan. |
| Melaksanakan Strategi | Kita menerapkan strategi yang telah direncanakan. | Pendapatan dari penjualan kue coklat: 120 kue x Rp 10.000/kue = Rp 1.200.000. Pendapatan dari penjualan kue vanila: 80 kue x Rp 8.000/kue = Rp 640.000. Total pendapatan: Rp 1.200.000 + Rp 640.000 = Rp 1.840.000. |
| Memeriksa Solusi | Kita perlu memastikan bahwa solusi yang diperoleh masuk akal. | Solusi yang diperoleh adalah Rp 1.840.000. Solusi ini masuk akal karena merupakan penjumlahan dari pendapatan penjualan kue coklat dan vanila. |
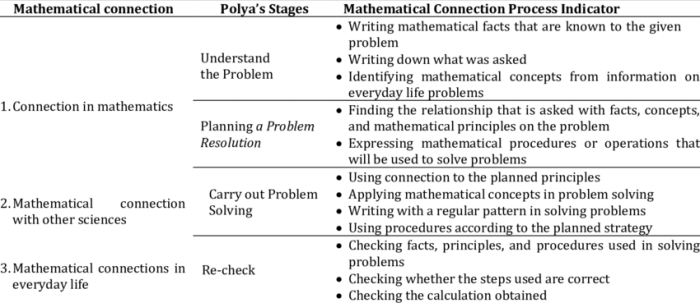
Hubungan Tahapan dengan Indikator Pemecahan Masalah, Indikator pemecahan masalah matematika
Setiap tahapan dalam pemecahan masalah matematika memiliki indikator yang dapat digunakan untuk menilai kemampuan siswa dalam memecahkan masalah. Berikut tabel yang menunjukkan hubungan antara setiap tahapan dengan indikator pemecahan masalah:
| Tahapan | Indikator Pemecahan Masalah |
|---|---|
| Memahami Masalah | – Mampu mengidentifikasi informasi yang diketahui dan yang ingin dicari. – Mampu menyatakan kembali masalah dengan kata-kata sendiri. – Mampu mengidentifikasi tujuan akhir dari soal. |
| Merencanakan Strategi | – Mampu memilih konsep, rumus, atau teknik yang relevan dengan masalah. – Mampu membuat rencana langkah-langkah yang akan dilakukan. – Mampu menjelaskan alasan di balik pilihan strategi. |
| Melaksanakan Strategi | – Mampu menerapkan strategi yang telah direncanakan dengan benar. – Mampu melakukan perhitungan, manipulasi aljabar, atau penggambaran diagram dengan tepat. – Mampu mencatat setiap langkah yang dilakukan. |
| Memeriksa Solusi | – Mampu memeriksa apakah solusi yang diperoleh masuk akal. – Mampu menguji kembali solusi yang diperoleh dengan memasukkannya ke dalam soal awal. – Mampu menjelaskan alasan mengapa solusi tersebut benar. |
Strategi Pemecahan Masalah Matematika: Indikator Pemecahan Masalah Matematika
Dalam dunia matematika, kemampuan memecahkan masalah merupakan keterampilan yang sangat penting. Bukan hanya tentang memahami rumus dan teorema, tetapi juga tentang bagaimana menerapkan pengetahuan tersebut dalam situasi yang beragam. Strategi pemecahan masalah membantu kita untuk mendekati masalah matematika dengan terstruktur dan sistematis, sehingga kita dapat menemukan solusi yang tepat dan efisien.
Memahami Masalah
Langkah pertama dalam memecahkan masalah matematika adalah memahami dengan baik apa yang diminta. Bacalah soal dengan cermat, identifikasi informasi yang diberikan, dan tentukan apa yang ingin kita cari. Kita juga dapat membuat diagram atau gambar untuk memvisualisasikan masalah dan membantu kita memahami hubungan antar variabel.
- Baca soal dengan cermat dan pahami konteksnya.
- Identifikasi informasi yang diberikan dan yang ingin dicari.
- Buat diagram atau gambar untuk memvisualisasikan masalah.
Menentukan Strategi
Setelah memahami masalah, kita perlu memilih strategi yang tepat untuk menyelesaikannya. Ada berbagai strategi yang dapat digunakan, tergantung pada jenis masalah dan tingkat kesulitannya.
1. Strategi Kerja Mundur
Strategi ini melibatkan memulai dari hasil yang diinginkan dan bekerja mundur untuk menemukan langkah-langkah yang diperlukan untuk mencapai hasil tersebut. Ini berguna untuk masalah yang melibatkan urutan langkah atau proses.
- Mulailah dari hasil yang diinginkan.
- Tentukan langkah-langkah yang diperlukan untuk mencapai hasil tersebut.
- Kerja mundur untuk menemukan langkah-langkah awal.
2. Strategi Mencari Pola
Strategi ini melibatkan pengamatan pola dalam data atau informasi yang diberikan. Pola tersebut dapat membantu kita untuk menemukan hubungan dan menentukan aturan yang berlaku. Strategi ini berguna untuk masalah yang melibatkan urutan atau deret angka.
- Amati data atau informasi yang diberikan.
- Cari pola atau hubungan antar data.
- Tentukan aturan yang berlaku berdasarkan pola yang ditemukan.
3. Strategi Simulasi
Strategi ini melibatkan pembuatan model atau representasi masalah yang lebih sederhana. Model ini dapat berupa diagram, tabel, atau persamaan. Strategi ini membantu kita untuk memvisualisasikan masalah dan menguji berbagai solusi.
- Buat model atau representasi masalah yang lebih sederhana.
- Uji berbagai solusi pada model tersebut.
- Analisis hasil simulasi untuk menemukan solusi yang tepat.
4. Strategi Mengubah Masalah
Strategi ini melibatkan mengubah masalah menjadi bentuk yang lebih sederhana atau lebih mudah diselesaikan. Ini dapat dilakukan dengan menggunakan rumus, teorema, atau prinsip matematika yang relevan.
- Ubah masalah menjadi bentuk yang lebih sederhana.
- Gunakan rumus, teorema, atau prinsip matematika yang relevan.
- Selesaikan masalah dalam bentuk yang lebih sederhana.
Menerapkan Strategi
Setelah memilih strategi yang tepat, kita perlu menerapkannya untuk menyelesaikan masalah. Hal ini melibatkan penggunaan rumus, operasi matematika, dan teknik pemecahan masalah yang relevan. Kita juga perlu memastikan bahwa langkah-langkah yang kita ambil logis dan konsisten.
Mengevaluasi Solusi
Setelah menemukan solusi, kita perlu mengevaluasinya untuk memastikan bahwa solusi tersebut benar dan masuk akal. Kita dapat melakukan ini dengan memeriksa kembali langkah-langkah yang kita ambil, membandingkan solusi dengan informasi yang diberikan, dan memeriksa apakah solusi tersebut memenuhi semua persyaratan masalah.
“Strategi pemecahan masalah merupakan kunci untuk membuka pintu menuju pemahaman matematika yang lebih dalam. Dengan memahami berbagai strategi dan menerapkannya dengan tepat, kita dapat mengatasi tantangan matematika dengan lebih mudah dan efektif.” – Prof. Dr. [Nama Pakar]
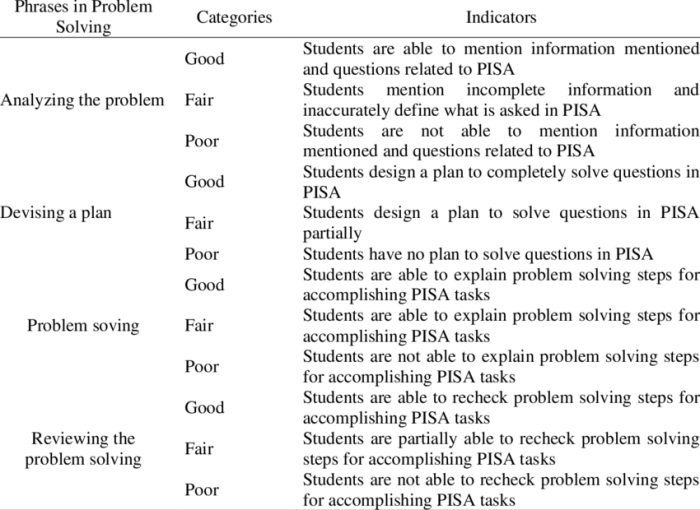
Penilaian Indikator Pemecahan Masalah Matematika

Penilaian terhadap indikator pemecahan masalah matematika penting untuk mengetahui sejauh mana siswa mampu menerapkan kemampuan berpikir kritis dan logis dalam menyelesaikan masalah matematika. Penilaian yang efektif dapat membantu guru dalam mengidentifikasi kekuatan dan kelemahan siswa, serta merancang strategi pembelajaran yang lebih efektif.
Metode Penilaian Indikator Pemecahan Masalah
Beberapa metode penilaian dapat digunakan untuk mengukur indikator pemecahan masalah matematika, antara lain:
- Tes tertulis: Tes tertulis dapat digunakan untuk menilai kemampuan siswa dalam memahami masalah, merumuskan strategi penyelesaian, dan mengeksekusi strategi tersebut. Tes tertulis dapat berbentuk soal cerita, soal pemecahan masalah kontekstual, atau soal yang membutuhkan pemahaman konsep matematika.
- Observasi: Guru dapat mengamati siswa saat mereka menyelesaikan masalah matematika. Observasi dapat dilakukan secara individual atau kelompok. Melalui observasi, guru dapat menilai kemampuan siswa dalam berkomunikasi, berkolaborasi, dan menggunakan alat bantu matematika.
- Portofolio: Portofolio berisi kumpulan karya siswa yang menunjukkan perkembangan kemampuan pemecahan masalah mereka. Portofolio dapat berisi soal-soal yang telah diselesaikan, catatan refleksi, dan hasil proyek.
- Presentasi: Siswa dapat mempresentasikan hasil pemecahan masalah mereka di depan kelas. Presentasi dapat membantu siswa dalam mengomunikasikan proses berpikir mereka dan menerima umpan balik dari teman sekelas dan guru.
Contoh Rubrik Penilaian
Rubrik penilaian dapat digunakan untuk menilai kemampuan pemecahan masalah siswa secara sistematis. Rubrik penilaian berisi kriteria yang digunakan untuk menilai setiap aspek kemampuan pemecahan masalah. Berikut adalah contoh rubrik penilaian untuk kemampuan memahami masalah:
| Kriteria | Sangat Baik (4) | Baik (3) | Cukup (2) | Perlu Perbaikan (1) |
|---|---|---|---|---|
| Kemampuan memahami masalah | Siswa dapat mengidentifikasi semua informasi penting dalam masalah dan merumuskan pertanyaan yang tepat. | Siswa dapat mengidentifikasi sebagian besar informasi penting dalam masalah dan merumuskan pertanyaan yang tepat. | Siswa dapat mengidentifikasi sebagian informasi penting dalam masalah dan merumuskan pertanyaan yang kurang tepat. | Siswa tidak dapat mengidentifikasi informasi penting dalam masalah dan tidak dapat merumuskan pertanyaan yang tepat. |
Rancangan Instrumen Penilaian
Instrumen penilaian yang dirancang untuk mengukur setiap indikator pemecahan masalah matematika harus sesuai dengan tujuan pembelajaran dan tingkat kesulitan siswa. Berikut adalah contoh rancangan instrumen penilaian untuk indikator “merumuskan strategi penyelesaian”:
Soal:
Sebuah toko menjual 2 jenis kue, kue A dan kue B. Kue A dijual dengan harga Rp 10.000 per buah dan kue B dijual dengan harga Rp 15.000 per buah. Ibu membeli 3 kue A dan 2 kue B. Berapakah total uang yang harus dibayar ibu?
Instrumen Penilaian:
Siswa diminta untuk menuliskan langkah-langkah yang akan mereka gunakan untuk menyelesaikan masalah tersebut. Berikut adalah contoh jawaban yang menunjukkan kemampuan merumuskan strategi penyelesaian yang baik:
1. Menghitung total harga kue A: 3 buah x Rp 10.000/buah = Rp 30.000
2. Menghitung total harga kue B: 2 buah x Rp 15.000/buah = Rp 30.000
3. Menjumlahkan total harga kue A dan kue B: Rp 30.000 + Rp 30.000 = Rp 60.000
Penerapan Indikator Pemecahan Masalah Matematika
Indikator pemecahan masalah matematika menjadi pedoman penting dalam mengukur kemampuan siswa dalam menyelesaikan masalah matematika. Penerapan indikator ini tidak hanya sebatas penilaian, namun juga dapat berperan aktif dalam proses pembelajaran matematika itu sendiri.
Penerapan Indikator dalam Berbagai Konteks Pembelajaran
Indikator pemecahan masalah matematika dapat diterapkan dalam berbagai konteks pembelajaran, baik di dalam maupun di luar kelas.
- Dalam Pembelajaran di Kelas: Indikator ini dapat digunakan sebagai acuan dalam menyusun soal-soal latihan, tugas, dan penilaian. Guru dapat merancang soal yang menantang siswa untuk mengidentifikasi masalah, merencanakan strategi, mengeksekusi solusi, dan mengevaluasi hasil. Selain itu, guru dapat memanfaatkan indikator untuk memberikan umpan balik yang spesifik kepada siswa tentang kekuatan dan kelemahan mereka dalam memecahkan masalah.
- Dalam Pembelajaran Berbasis Proyek: Indikator ini dapat menjadi kerangka kerja dalam merancang proyek-proyek matematika yang menuntut siswa untuk menyelesaikan masalah dunia nyata. Misalnya, dalam proyek tentang optimasi ruang kelas, siswa dapat menggunakan indikator untuk mengidentifikasi masalah, mencari informasi, menganalisis data, dan menyusun solusi yang optimal.
- Dalam Pembelajaran Kolaboratif: Indikator ini dapat membantu siswa untuk bekerja sama dalam memecahkan masalah matematika secara efektif. Dengan menggunakan indikator, siswa dapat membagi tugas, saling membantu, dan saling memberikan masukan dalam proses pemecahan masalah.
Ilustrasi Penerapan Indikator Pemecahan Masalah
Berikut adalah ilustrasi bagaimana indikator pemecahan masalah dapat membantu siswa dalam menyelesaikan masalah matematika:
Misalkan, siswa diberikan soal: “Sebuah toko kue menjual 2 jenis kue, kue A dan kue B. Kue A dijual dengan harga Rp. 10.000 per kotak dan kue B dijual dengan harga Rp. 15.000 per kotak. Jika toko kue tersebut berhasil menjual 50 kotak kue A dan 30 kotak kue B, berapa total pendapatan toko kue tersebut?”
Dengan menggunakan indikator pemecahan masalah, siswa dapat menyelesaikan soal tersebut dengan langkah-langkah berikut:
- Memahami Masalah: Siswa memahami bahwa soal meminta mereka untuk menghitung total pendapatan toko kue dari penjualan kue A dan kue B.
- Merencanakan Strategi: Siswa merencanakan strategi untuk menyelesaikan masalah dengan mengalikan jumlah kotak kue A dengan harga per kotak, mengalikan jumlah kotak kue B dengan harga per kotak, dan kemudian menjumlahkan kedua hasil tersebut.
- Mengeksekusi Solusi: Siswa mengeksekusi solusi dengan menghitung: (50 kotak x Rp. 10.000/kotak) + (30 kotak x Rp. 15.000/kotak) = Rp. 500.000 + Rp. 450.000 = Rp. 950.000.
- Mengevaluasi Hasil: Siswa mengevaluasi hasil dengan memastikan bahwa jawabannya masuk akal dan sesuai dengan konteks soal. Dalam hal ini, jawaban Rp. 950.000 masuk akal karena merupakan penjumlahan dari pendapatan penjualan kue A dan kue B.
Contoh Kegiatan Pembelajaran untuk Mengembangkan Kemampuan Pemecahan Masalah
Berikut adalah contoh kegiatan pembelajaran yang dirancang untuk mengembangkan kemampuan pemecahan masalah siswa:
Kegiatan: “Menyusun Strategi Pembelian Bahan Bangunan”
Tujuan: Membantu siswa untuk menerapkan indikator pemecahan masalah dalam konteks kehidupan sehari-hari.
Langkah-langkah:
- Membagi siswa ke dalam kelompok-kelompok kecil. Setiap kelompok diberikan skenario yang berbeda tentang kebutuhan bahan bangunan untuk membangun rumah, seperti:
- Kelompok 1: Membangun rumah sederhana dengan luas 50 meter persegi.
- Kelompok 2: Membangun rumah minimalis dengan luas 75 meter persegi.
- Kelompok 3: Membangun rumah mewah dengan luas 100 meter persegi.
- Siswa diminta untuk mencari informasi tentang harga bahan bangunan, seperti batu bata, semen, pasir, besi, dan kayu.
- Siswa diminta untuk merencanakan strategi pembelian bahan bangunan, dengan mempertimbangkan kebutuhan, anggaran, dan ketersediaan bahan.
- Siswa diminta untuk mempresentasikan rencana pembelian bahan bangunan mereka, dengan menjelaskan alasan di balik strategi yang mereka pilih.
- Guru memberikan umpan balik dan arahan, dengan fokus pada penerapan indikator pemecahan masalah dalam proses perencanaan dan pengambilan keputusan.
Pemungkas
Pemahaman yang mendalam tentang indikator pemecahan masalah matematika membantu kita mengasah kemampuan berpikir kritis, meningkatkan kemampuan memecahkan masalah, dan menemukan solusi kreatif untuk berbagai tantangan. Indikator ini bukan hanya alat ukur, tetapi juga peta jalan yang membantu kita menjelajahi dunia matematika dengan lebih efektif dan menyenangkan.





