Integral Contoh Soal: Memahami Konsep dan Penerapannya

Integral contoh soal – Pernahkah Anda bertanya-tanya bagaimana matematika dapat membantu kita memahami dunia nyata? Integral, salah satu konsep penting dalam kalkulus, memegang kunci untuk menjawab pertanyaan ini. Integral adalah alat yang ampuh untuk menghitung luas, volume, dan berbagai besaran lainnya, yang diterapkan dalam berbagai bidang seperti fisika, ekonomi, dan teknik.

Dalam artikel ini, kita akan menjelajahi dunia integral dengan contoh-contoh soal yang menarik. Mulai dari pengertian dasar hingga teknik integrasi dan penerapannya dalam berbagai disiplin ilmu, kita akan mengupas konsep integral secara mendalam. Siap untuk merasakan kekuatan kalkulus dalam menyelesaikan masalah dunia nyata?

Jenis-jenis Integral

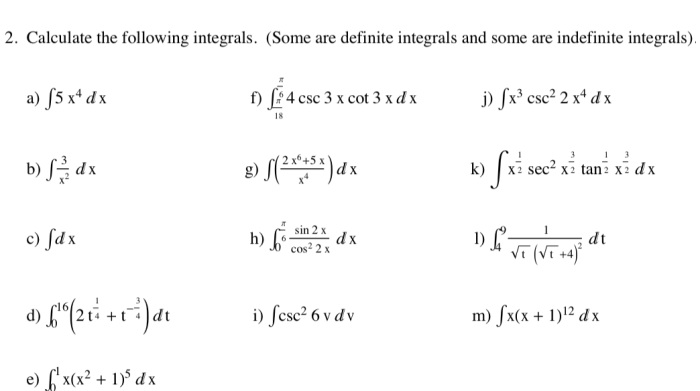
Integral merupakan konsep penting dalam kalkulus yang digunakan untuk menghitung luas area, volume benda putar, dan berbagai aplikasi lainnya. Integral dapat diklasifikasikan menjadi beberapa jenis berdasarkan bentuk dan cara penyelesaiannya. Berikut ini adalah beberapa jenis integral yang umum dipelajari:

Integral Tak Tentu

Integral tak tentu merupakan operasi kebalikan dari turunan. Hasil dari integral tak tentu adalah fungsi yang turunannya adalah integran.

Integral tak tentu ditandai dengan simbol ∫ (tanda integral).

∫ f(x) dx = F(x) + C

di mana f(x) adalah integran, F(x) adalah antiturunan dari f(x), dan C adalah konstanta integrasi.

Contoh soal:
Tentukan integral tak tentu dari f(x) = 2x + 1.

Penyelesaian:
∫ (2x + 1) dx = x^2 + x + C

Integral Tentu

Integral tentu merupakan integral yang memiliki batas atas dan batas bawah integrasi. Hasil dari integral tentu adalah nilai numerik yang mewakili luas area di bawah kurva fungsi integran.

Integral tentu ditandai dengan simbol ∫a^b (tanda integral dengan batas atas b dan batas bawah a).

∫a^b f(x) dx = F(b) – F(a)

di mana f(x) adalah integran, F(x) adalah antiturunan dari f(x), dan a dan b adalah batas bawah dan batas atas integrasi.

Contoh soal:
Tentukan integral tentu dari f(x) = x^2 dari x = 0 hingga x = 2.

Penyelesaian:
∫0^2 x^2 dx = (2^3)/3 – (0^3)/3 = 8/3

Integral Ganda

Integral ganda digunakan untuk menghitung volume benda tiga dimensi. Integral ganda melibatkan integrasi terhadap dua variabel, biasanya x dan y.

∫R ∫S f(x,y) dx dy

di mana R dan S adalah batas integrasi untuk x dan y, dan f(x,y) adalah fungsi integran.

Contoh soal:
Tentukan volume benda yang dibatasi oleh bidang z = x^2 + y^2, bidang x = 0, bidang y = 0, dan bidang x + y = 1.

Penyelesaian:
Volume benda dapat dihitung dengan integral ganda:
∫0^1 ∫0^(1-x) (x^2 + y^2) dy dx

Integral Lipat

Integral lipat merupakan integral yang melibatkan lebih dari dua variabel. Integral lipat digunakan untuk menghitung volume benda berdimensi lebih tinggi, seperti volume benda empat dimensi.

∫R ∫S ∫T f(x,y,z) dx dy dz

di mana R, S, dan T adalah batas integrasi untuk x, y, dan z, dan f(x,y,z) adalah fungsi integran.

Contoh soal:
Tentukan volume benda yang dibatasi oleh bidang z = x^2 + y^2 + z^2, bidang x = 0, bidang y = 0, bidang z = 0, dan bidang x + y + z = 1.

Penyelesaian:
Volume benda dapat dihitung dengan integral lipat:
∫0^1 ∫0^(1-x) ∫0^(1-x-y) (x^2 + y^2 + z^2) dz dy dx

Integral Garis

Integral garis digunakan untuk menghitung panjang kurva, luas permukaan, dan kerja yang dilakukan oleh gaya sepanjang kurva. Integral garis melibatkan integrasi terhadap satu variabel, biasanya t, yang merupakan parameterisasi kurva.

∫C f(x(t),y(t)) ds

di mana C adalah kurva yang diparameterisasi oleh x(t) dan y(t), f(x,y) adalah fungsi integran, dan ds adalah elemen panjang busur.

Contoh soal:
Tentukan panjang kurva y = x^2 dari x = 0 hingga x = 1.

Penyelesaian:
Panjang kurva dapat dihitung dengan integral garis:
∫0^1 ∫ (1 + (2x)^2)^1/2 dx

Integral Permukaan

Integral permukaan digunakan untuk menghitung luas permukaan, fluks, dan berbagai aplikasi lainnya pada permukaan tiga dimensi. Integral permukaan melibatkan integrasi terhadap dua variabel, biasanya u dan v, yang merupakan parameterisasi permukaan.

∫S f(x(u,v),y(u,v),z(u,v)) dS

di mana S adalah permukaan yang diparameterisasi oleh x(u,v), y(u,v), dan z(u,v), f(x,y,z) adalah fungsi integran, dan dS adalah elemen luas permukaan.

Contoh soal:
Tentukan luas permukaan bola x^2 + y^2 + z^2 = 1.

Penyelesaian:
Luas permukaan bola dapat dihitung dengan integral permukaan:
∫S 1 dS

Teknik Integrasi: Integral Contoh Soal

Integrasi dalam kalkulus merupakan proses menemukan antiturunan dari suatu fungsi. Namun, tidak semua fungsi memiliki antiturunan yang dapat ditemukan secara langsung dengan menggunakan aturan dasar integrasi. Oleh karena itu, berbagai teknik integrasi dikembangkan untuk mengatasi permasalahan ini. Teknik-teknik ini memungkinkan kita untuk mengubah bentuk fungsi menjadi bentuk yang lebih sederhana dan mudah diintegrasikan.

Teknik Integrasi Umum

Berikut beberapa teknik integrasi yang umum digunakan dalam kalkulus:

• Substitusi: Teknik ini melibatkan penggantian variabel dalam integral dengan fungsi lain, sehingga menghasilkan bentuk integral yang lebih sederhana. Teknik ini sangat berguna untuk mengintegrasikan fungsi-fungsi yang melibatkan komposisi fungsi.
• Integrasi Parsial: Teknik ini digunakan untuk mengintegrasikan fungsi-fungsi yang merupakan hasil perkalian dari dua fungsi. Teknik ini melibatkan penguraian integral menjadi dua bagian, yang kemudian diintegrasikan secara terpisah.
• Integrasi Trigonometri: Teknik ini digunakan untuk mengintegrasikan fungsi-fungsi trigonometri. Teknik ini melibatkan penggunaan identitas trigonometri untuk mengubah bentuk fungsi menjadi bentuk yang lebih sederhana.
• Integrasi Fraksi Parsial: Teknik ini digunakan untuk mengintegrasikan fungsi-fungsi yang merupakan hasil pembagian dari dua polinomial. Teknik ini melibatkan penguraian fungsi menjadi beberapa fraksi parsial yang lebih sederhana.

Contoh Soal Substitusi

Misalkan kita ingin menghitung integral dari fungsi berikut:

∫(2x + 1)² dx

Kita dapat menggunakan teknik substitusi untuk menyelesaikan integral ini. Langkah-langkahnya sebagai berikut:

1. Substitusi: Misalkan u = 2x + 1. Maka, du = 2 dx.
2. Ubah Integral: Substitusikan u dan du ke dalam integral asli. Kita peroleh:

   ∫(2x + 1)² dx = ∫u² (du/2)

3. Integrasi: Integrasikan u² (du/2). Kita peroleh:

   ∫u² (du/2) = (1/6) u³ + C

4. Kembalikan ke Variabel Asli: Substitusikan kembali u = 2x + 1 ke dalam hasil integrasi. Kita peroleh:

   (1/6) u³ + C = (1/6) (2x + 1)³ + C

   Jadi, integral dari (2x + 1)² dx adalah (1/6) (2x + 1)³ + C.

   Mengerti konsep integral memang butuh latihan, dan contoh soal bisa jadi kunci untuk mengasah kemampuanmu. Nah, untuk memahami cara menghitung integral, kamu bisa coba latihan soal yang melibatkan angka indeks, seperti yang dibahas di contoh soal angka indeks.

   Konsep ini bisa diterapkan dalam berbagai macam soal integral, jadi memahami angka indeks bisa membantumu untuk menyelesaikan soal integral yang lebih kompleks.

Integral dalam Ekonomi

Integral merupakan konsep matematika yang penting dalam ekonomi, khususnya dalam analisis marginal dan produksi. Integral memungkinkan kita untuk menghitung luas di bawah kurva, yang memiliki aplikasi praktis dalam ekonomi.

Analisis Marginal

Analisis marginal mengkaji perubahan kecil dalam variabel ekonomi, seperti perubahan dalam produksi atau konsumsi, dan bagaimana perubahan ini memengaruhi variabel lain, seperti keuntungan atau utilitas. Integral berperan penting dalam analisis marginal karena membantu kita menghitung perubahan total dalam suatu variabel, mengingat perubahan marginalnya.

Misalnya, integral dapat digunakan untuk menghitung total biaya produksi dari perubahan kecil dalam jumlah barang yang diproduksi. Integral juga dapat digunakan untuk menghitung total pendapatan dari perubahan kecil dalam jumlah barang yang dijual.

Produksi, Integral contoh soal

Integral juga berperan penting dalam analisis produksi. Integral dapat digunakan untuk menghitung total output yang dihasilkan dari suatu proses produksi, mengingat fungsi produksi marginal. Fungsi produksi marginal menunjukkan perubahan dalam output yang dihasilkan dari perubahan kecil dalam input.

Integral dapat digunakan untuk menghitung total output yang dihasilkan dari suatu proses produksi, mengingat fungsi produksi marginal. Fungsi produksi marginal menunjukkan perubahan dalam output yang dihasilkan dari perubahan kecil dalam input.

Contoh Soal Fungsi Permintaan

Permintaan adalah hubungan antara harga suatu barang dan jumlah barang yang ingin dibeli konsumen pada harga tersebut. Fungsi permintaan dapat diwakili oleh persamaan matematika, dan integral dapat digunakan untuk menghitung total jumlah barang yang diminta pada rentang harga tertentu.

Misalnya, perhatikan fungsi permintaan berikut:

Q = 100 – 2P

di mana Q adalah jumlah barang yang diminta dan P adalah harga.

Integral dapat digunakan untuk menghitung total jumlah barang yang diminta pada rentang harga dari 10 hingga 20.

∫(100 – 2P) dP dari 10 hingga 20

= (100P – P^2) dari 10 hingga 20

= (100(20) – 20^2) – (100(10) – 10^2)

= 1600 – 900

= 700

Hasilnya menunjukkan bahwa total jumlah barang yang diminta pada rentang harga dari 10 hingga 20 adalah 700 unit.

Contoh Soal Fungsi Penawaran

Penawaran adalah hubungan antara harga suatu barang dan jumlah barang yang ingin dijual produsen pada harga tersebut. Fungsi penawaran juga dapat diwakili oleh persamaan matematika, dan integral dapat digunakan untuk menghitung total jumlah barang yang ditawarkan pada rentang harga tertentu.

Misalnya, perhatikan fungsi penawaran berikut:

Q = 50 + 3P

di mana Q adalah jumlah barang yang ditawarkan dan P adalah harga.

Integral dapat digunakan untuk menghitung total jumlah barang yang ditawarkan pada rentang harga dari 15 hingga 25.

∫(50 + 3P) dP dari 15 hingga 25

= (50P + 1.5P^2) dari 15 hingga 25

= (50(25) + 1.5(25)^2) – (50(15) + 1.5(15)^2)

= 2125 – 1312.5

= 812.5

Hasilnya menunjukkan bahwa total jumlah barang yang ditawarkan pada rentang harga dari 15 hingga 25 adalah 812.5 unit.

Penutup

Dengan memahami konsep integral, kita membuka pintu menuju pemahaman yang lebih dalam tentang dunia di sekitar kita. Integral tidak hanya sekadar rumus matematika, tetapi alat yang ampuh untuk menyelesaikan berbagai masalah kompleks. Dari menghitung luas daerah hingga memprediksi perilaku sistem fisik, integral memainkan peran penting dalam kemajuan ilmu pengetahuan dan teknologi.