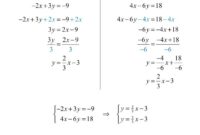Judul skripsi matematika murni – Matematika, ilmu yang penuh misteri dan keindahan, terbagi menjadi dua cabang besar: matematika murni dan matematika terapan. Matematika murni, yang seringkali dianggap sebagai “matematika untuk matematika itu sendiri”, menjelajahi dunia abstrak konsep-konsep matematis tanpa terikat pada aplikasi praktis. Jika Anda ingin menggali lebih dalam dunia abstrak ini dan menuangkannya dalam sebuah skripsi, maka artikel ini akan menjadi panduan yang tepat untuk Anda.
Skripsi matematika murni, seperti namanya, berfokus pada eksplorasi konsep-konsep matematis murni tanpa terikat pada aplikasi praktis. Skripsi ini bisa membahas berbagai topik, mulai dari teori bilangan, aljabar abstrak, topologi, hingga analisis. Pengembangan teori-teori baru, pembuktian teorema, dan penyelesaian masalah matematika yang rumit menjadi fokus utama dalam skripsi matematika murni.
Pengertian Matematika Murni
Matematika murni merupakan cabang ilmu matematika yang fokus pada pengembangan konsep dan teori matematika secara abstrak, tanpa langsung menerapkannya pada masalah dunia nyata. Berbeda dengan matematika terapan yang berfokus pada aplikasi matematika untuk memecahkan masalah di bidang lain, matematika murni bertujuan untuk memahami struktur dan hubungan matematis secara mendalam.
Bidang-bidang dalam Matematika Murni
Matematika murni mencakup berbagai bidang, mulai dari aljabar abstrak hingga teori bilangan, geometri, dan analisis. Berikut beberapa contoh bidang dalam matematika murni dan kaitannya dengan penelitian skripsi:
- Aljabar Abstrak: Berfokus pada struktur aljabar seperti grup, ring, dan lapangan. Penelitian skripsi dalam bidang ini bisa membahas tentang sifat-sifat grup, homomorfisma, atau teori Galois.
- Teori Bilangan: Menjelajahi sifat-sifat bilangan bulat, termasuk teori bilangan prima, persamaan Diophantine, dan teori bilangan analitik. Penelitian skripsi dalam bidang ini bisa membahas tentang pembuktian teorema baru tentang bilangan prima atau aplikasi teori bilangan dalam kriptografi.
- Geometri: Mempelajari bentuk dan ruang, termasuk geometri Euclidean, geometri non-Euclidean, dan topologi. Penelitian skripsi dalam bidang ini bisa membahas tentang sifat-sifat ruang, kurva, atau permukaan.
- Analisis: Berfokus pada konsep limit, kontinuitas, dan diferensial. Penelitian skripsi dalam bidang ini bisa membahas tentang solusi persamaan diferensial, teori fungsi kompleks, atau analisis fungsional.
Sejarah Singkat Perkembangan Matematika Murni
Matematika murni telah berkembang selama berabad-abad, dipengaruhi oleh berbagai peradaban. Beberapa tokoh penting dalam sejarah matematika murni antara lain:
- Yunani Kuno: Pythagoras, Euclid, dan Archimedes mengembangkan konsep geometri, teori bilangan, dan kalkulus awal.
- Zaman Pertengahan: Al-Khwarizmi dari Persia mengembangkan aljabar, sementara matematikawan India mengembangkan sistem angka desimal.
- Zaman Modern: Isaac Newton dan Gottfried Wilhelm Leibniz mengembangkan kalkulus modern, sementara matematikawan abad ke-19 seperti Georg Cantor dan Bernhard Riemann mengembangkan konsep set dan topologi.
Perkembangan matematika murni telah memberikan pengaruh yang besar pada bidang lain, seperti fisika, komputer, dan ekonomi. Misalnya, teori bilangan digunakan dalam kriptografi, sedangkan kalkulus digunakan dalam pemodelan fisik dan ekonomi. Matematika murni juga memberikan landasan teoretis untuk banyak teknologi modern.
Topik Skripsi Matematika Murni

Memilih topik skripsi matematika murni merupakan langkah awal yang penting dalam perjalanan akademik. Bidang ini menawarkan berbagai pilihan menarik yang menantang sekaligus memuaskan rasa ingin tahu. Artikel ini akan mengulas beberapa topik skripsi umum yang dipelajari dalam matematika murni, serta memberikan contoh konkret dalam teori bilangan dan aljabar abstrak.
Topik Skripsi Umum dalam Matematika Murni
Matematika murni merupakan cabang matematika yang berfokus pada konsep-konsep abstrak dan struktur matematis. Topik yang dipelajari dalam matematika murni sangat beragam, meliputi:
- Teori Bilangan: Membahas sifat-sifat bilangan bulat, seperti pembagian, faktorisasi, dan persamaan diophantine. Topik ini juga mencakup bilangan prima, fungsi aritmetika, dan teori modular.
- Aljabar Abstrak: Mempelajari struktur aljabar, seperti grup, gelanggang, dan lapangan. Topik ini meliputi teori homomorfisma, grup simetri, dan aljabar linear.
- Analisis Real dan Kompleks: Membahas konsep-konsep limit, kontinuitas, diferensial, dan integral dalam konteks bilangan real dan kompleks. Topik ini meliputi deret fungsi, teori ukuran, dan analisis Fourier.
- Topologi: Mempelajari konsep-konsep ruang topologi, seperti keterhubungan, kekompakan, dan kontinuitas. Topik ini meliputi topologi aljabar, teori manifold, dan geometri diferensial.
- Geometri: Membahas konsep-konsep ruang geometri, seperti jarak, sudut, dan bentuk. Topik ini meliputi geometri Euclidean, geometri non-Euclidean, dan geometri diferensial.
- Logika Matematika: Mempelajari dasar-dasar logika dan teori himpunan. Topik ini meliputi sistem deduksi, teori model, dan teori rekursi.
Contoh Topik Skripsi Matematika Murni dalam Teori Bilangan
Teori bilangan merupakan bidang yang kaya dengan masalah terbuka dan topik menarik untuk dikaji. Berikut contoh topik skripsi yang berfokus pada teori bilangan:
“Analisis Algoritma Faktorisasi Bilangan Bulat Besar Menggunakan Metode Sieve of Eratosthenes dan Metode Pollard-Rho”
Topik ini membahas analisis algoritma faktorisasi bilangan bulat besar dengan menggunakan dua metode klasik, yaitu Sieve of Eratosthenes dan Pollard-Rho. Penelitian ini dapat mencakup:
- Implementasi algoritma faktorisasi dalam bahasa pemrograman tertentu.
- Perbandingan kinerja kedua algoritma dalam faktorisasi bilangan bulat besar.
- Analisis kompleksitas waktu dan ruang dari kedua algoritma.
Contoh Topik Skripsi Matematika Murni dalam Aljabar Abstrak
Aljabar abstrak menawarkan banyak konsep dan struktur yang dapat dikaji lebih dalam. Berikut contoh topik skripsi yang berfokus pada aljabar abstrak:
“Aplikasi Teori Grup dalam Kode Koreksi Kesalahan”
Topik ini membahas aplikasi teori grup dalam kode koreksi kesalahan, yang digunakan untuk mendeteksi dan memperbaiki kesalahan dalam transmisi data. Penelitian ini dapat mencakup:
- Pengembangan kode koreksi kesalahan berbasis grup tertentu.
- Analisis jarak minimum dan kemampuan koreksi kesalahan dari kode tersebut.
- Implementasi kode koreksi kesalahan dalam simulasi transmisi data.
Metode Penelitian Skripsi

Metode penelitian merupakan jantung dari sebuah skripsi. Dalam skripsi matematika murni, metode penelitian yang digunakan berperan penting dalam mengungkap kebenaran dan menemukan solusi atas permasalahan yang dikaji. Metode yang tepat akan menghasilkan data yang valid dan analisis yang kuat, sehingga kesimpulan yang diperoleh dapat dipertanggungjawabkan.
Metode Penelitian Umum dalam Skripsi Matematika Murni
Beberapa metode penelitian umum yang digunakan dalam skripsi matematika murni antara lain:
- Metode Deduktif: Metode ini diawali dengan teori atau prinsip umum, kemudian dijabarkan dan diterapkan pada kasus khusus. Misalnya, dalam skripsi yang membahas tentang sifat-sifat grup, peneliti dapat memulai dengan definisi dan teorema dasar tentang grup, lalu mengaplikasikannya pada contoh-contoh grup spesifik.
- Metode Induktif: Metode ini berfokus pada pengumpulan data dan observasi dari kasus-kasus khusus, lalu menarik kesimpulan umum berdasarkan data yang diperoleh. Misalnya, peneliti dapat menganalisis beberapa contoh polinomial, lalu menemukan pola umum yang berlaku untuk semua polinomial dengan karakteristik tertentu.
- Metode Historis: Metode ini digunakan untuk menelusuri perkembangan suatu konsep atau teori matematika dari masa ke masa. Misalnya, peneliti dapat meneliti sejarah perkembangan konsep integral, mulai dari penemuannya hingga perkembangannya hingga saat ini.
- Metode Deskriptif: Metode ini bertujuan untuk menggambarkan dan menganalisis suatu fenomena matematika secara sistematis dan objektif. Misalnya, peneliti dapat mendeskripsikan dan menganalisis sifat-sifat geometri non-Euclidean, seperti geometri bola.
Contoh Metode Deduktif dan Induktif
Berikut adalah contoh penerapan metode deduktif dan induktif dalam skripsi matematika murni:
Metode Deduktif
Misalnya, dalam skripsi yang membahas tentang teorema Pythagoras, peneliti dapat memulai dengan teorema Pythagoras sebagai prinsip umum, kemudian menerapkannya pada kasus khusus seperti mencari panjang sisi miring segitiga siku-siku.
Teorema Pythagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat sisi miring sama dengan jumlah kuadrat kedua sisi lainnya.
Peneliti kemudian dapat mengaplikasikan teorema ini untuk menghitung panjang sisi miring segitiga siku-siku dengan panjang sisi alas 3 cm dan tinggi 4 cm.
Metode Induktif
Misalnya, dalam skripsi yang membahas tentang pola bilangan Fibonacci, peneliti dapat mengamati beberapa suku pertama barisan Fibonacci, yaitu 1, 1, 2, 3, 5, 8, 13, dan seterusnya. Dari pengamatan ini, peneliti dapat menemukan pola bahwa setiap suku berikutnya adalah hasil penjumlahan dari dua suku sebelumnya.
Berdasarkan pola yang ditemukan, peneliti kemudian dapat menarik kesimpulan bahwa barisan Fibonacci mengikuti pola tersebut untuk semua suku berikutnya.
Perbandingan Metode Kuantitatif dan Kualitatif
| Aspek | Kuantitatif | Kualitatif |
|---|---|---|
| Tujuan | Mengukur dan menganalisis data numerik | Mendeskripsikan dan menginterpretasikan data non-numerik |
| Metode Pengumpulan Data | Kuesioner, tes, observasi terstruktur | Wawancara, observasi non-terstruktur, studi kasus |
| Analisis Data | Statistik, analisis matematis | Analisis tematik, analisis naratif |
| Contoh dalam Skripsi Matematika Murni | Menganalisis pengaruh metode pembelajaran terhadap hasil belajar matematika | Menganalisis pengaruh budaya terhadap pemahaman konsep matematika |
Struktur Skripsi Matematika Murni: Judul Skripsi Matematika Murni
Skripsi matematika murni merupakan karya tulis ilmiah yang membahas topik tertentu dalam bidang matematika murni. Struktur skripsi ini umumnya terdiri dari beberapa bab yang saling terkait, membentuk alur pembahasan yang sistematis dan logis.
Bab Pendahuluan
Bab pendahuluan merupakan bagian awal skripsi yang berfungsi sebagai pengantar bagi pembaca untuk memahami keseluruhan isi skripsi. Bab ini biasanya terdiri dari beberapa bagian penting, yaitu:
- Latar Belakang: Berisi penjelasan tentang topik yang akan dibahas, mengapa topik tersebut penting untuk diteliti, dan apa relevansinya dengan bidang matematika murni.
- Rumusan Masalah: Merupakan pertanyaan spesifik yang akan dijawab dalam skripsi. Rumusan masalah harus dirumuskan dengan jelas, singkat, dan terarah.
- Tujuan Penelitian: Menyatakan tujuan yang ingin dicapai dalam penelitian ini. Tujuan penelitian harus sesuai dengan rumusan masalah dan dapat dicapai melalui metode penelitian yang digunakan.
- Manfaat Penelitian: Menjelaskan manfaat yang diharapkan dari hasil penelitian ini, baik bagi pengembangan ilmu pengetahuan, dunia pendidikan, maupun bagi masyarakat luas.
Bab Tinjauan Pustaka, Judul skripsi matematika murni
Bab tinjauan pustaka membahas berbagai teori, konsep, dan hasil penelitian terdahulu yang relevan dengan topik yang diteliti. Tinjauan pustaka ini bertujuan untuk memberikan landasan teoritis bagi penelitian dan membantu dalam memahami konteks penelitian.
- Pembahasan teori: Berisi penjelasan tentang teori-teori yang relevan dengan topik penelitian, termasuk definisi, konsep, dan prinsip-prinsip yang mendasari teori tersebut.
- Pembahasan penelitian terdahulu: Berisi ulasan tentang penelitian-penelitian terdahulu yang relevan dengan topik penelitian. Ulasan ini meliputi metode penelitian, hasil penelitian, dan kesimpulan yang diperoleh dari penelitian terdahulu.
- Kerangka pemikiran: Merupakan kerangka konseptual yang menghubungkan teori-teori dan hasil penelitian terdahulu dengan topik penelitian yang akan dibahas. Kerangka pemikiran ini berfungsi sebagai landasan bagi pengembangan metode penelitian dan analisis data.
Bab Metode Penelitian
Bab metode penelitian menjelaskan langkah-langkah yang digunakan dalam penelitian, termasuk metode pengumpulan data, metode analisis data, dan teknik pengolahan data.
- Metode Penelitian: Menjelaskan jenis penelitian yang digunakan, misalnya penelitian kualitatif, kuantitatif, atau campuran.
- Sumber Data: Menjelaskan jenis data yang digunakan dalam penelitian, misalnya data primer, data sekunder, atau kombinasi keduanya.
- Teknik Pengumpulan Data: Menjelaskan teknik yang digunakan untuk mengumpulkan data, misalnya observasi, wawancara, kuesioner, studi dokumentasi, atau analisis literatur.
- Teknik Analisis Data: Menjelaskan teknik yang digunakan untuk menganalisis data, misalnya analisis deskriptif, analisis inferensial, atau analisis kualitatif.
- Teknik Pengolahan Data: Menjelaskan teknik yang digunakan untuk mengolah data, misalnya tabulasi, pengelompokan, atau pengkodean data.
Bab Hasil dan Pembahasan
Bab hasil dan pembahasan merupakan inti dari skripsi. Bab ini menyajikan hasil penelitian yang diperoleh melalui analisis data, dan dilanjutkan dengan pembahasan yang mendalam tentang makna dan implikasi dari hasil penelitian tersebut.
- Hasil Penelitian: Menyajikan hasil penelitian secara sistematis dan objektif, sesuai dengan metode penelitian yang digunakan. Hasil penelitian disajikan dalam bentuk tabel, grafik, atau teks, tergantung pada jenis data yang dianalisis.
- Pembahasan: Menginterpretasikan hasil penelitian, menghubungkannya dengan teori-teori dan penelitian terdahulu, serta membahas implikasi dan keterbatasan dari hasil penelitian. Pembahasan harus dilakukan secara kritis dan analitis, dengan mempertimbangkan berbagai faktor yang relevan.
Bab Penutup
Bab penutup merupakan bagian akhir dari skripsi yang berisi kesimpulan dan saran. Kesimpulan merangkum hasil penelitian dan menjawab rumusan masalah yang diajukan. Saran berisi rekomendasi yang dapat digunakan untuk penelitian selanjutnya atau untuk pengembangan ilmu pengetahuan di bidang yang terkait.
Contoh Format Penulisan Bab Pendahuluan
Berikut adalah contoh format penulisan bab pendahuluan dalam skripsi matematika murni:
BAB I PENDAHULUAN
1.1 Latar Belakang
Isi paragraf latar belakang
1.2 Rumusan Masalah
Isi paragraf rumusan masalah
1.3 Tujuan Penelitian
Isi paragraf tujuan penelitian
1.4 Manfaat Penelitian
Isi paragraf manfaat penelitian
Contoh Format Penulisan Daftar Pustaka dan Lampiran
Berikut adalah tabel yang berisi contoh format penulisan daftar pustaka dan lampiran dalam skripsi matematika murni:
| Bagian | Contoh Format |
|---|---|
| Daftar Pustaka |
|
| Lampiran |
|
Sumber Referensi
Menyusun skripsi matematika murni memerlukan landasan yang kuat, dan sumber referensi yang tepat adalah kunci utamanya. Sumber referensi yang kredibel dan terpercaya menjadi bukti kuat bagi argumen dan pembahasan dalam skripsi.
Contoh Buku dan Jurnal Ilmiah
Berikut beberapa contoh buku dan jurnal ilmiah yang relevan dengan skripsi matematika murni:
- Buku:
- “Algebra Linear” oleh Gilbert Strang – Buku ini membahas konsep dasar aljabar linear, yang merupakan topik penting dalam matematika murni.
- “Calculus” oleh James Stewart – Buku ini membahas kalkulus, salah satu cabang utama matematika yang memiliki aplikasi luas dalam berbagai bidang.
- “Introduction to Topology” oleh James Munkres – Buku ini membahas topologi, cabang matematika yang mempelajari sifat-sifat ruang dan bentuk.
- Jurnal Ilmiah:
- “Journal of the American Mathematical Society” – Jurnal ini memuat penelitian terkini dalam berbagai bidang matematika, termasuk matematika murni.
- “Annals of Mathematics” – Jurnal ini merupakan salah satu jurnal matematika paling bergengsi di dunia, yang menerbitkan penelitian tingkat tinggi dalam berbagai bidang matematika, termasuk matematika murni.
- “Mathematical Proceedings of the Cambridge Philosophical Society” – Jurnal ini memuat penelitian dalam berbagai bidang matematika, termasuk matematika murni, khususnya bidang aljabar, geometri, dan analisis.
Cara Mencari Sumber Referensi
Mencari sumber referensi yang kredibel dan terpercaya untuk skripsi matematika murni dapat dilakukan melalui beberapa cara:
- Perpustakaan Universitas: Perpustakaan universitas biasanya memiliki koleksi buku dan jurnal ilmiah yang lengkap, termasuk dalam bidang matematika murni.
- Basis Data Ilmiah: Basis data ilmiah seperti MathSciNet dan Scopus menyediakan akses ke abstrak dan daftar referensi dari berbagai jurnal ilmiah, termasuk jurnal matematika.
- Website Resmi Lembaga Penelitian: Website resmi lembaga penelitian seperti American Mathematical Society (AMS) dan Institute of Mathematical Statistics (IMS) menyediakan akses ke publikasi dan sumber daya lainnya yang relevan dengan matematika murni.
- Gugus Penelitian Matematika: Berdiskusi dengan dosen pembimbing dan anggota gugus penelitian matematika dapat membantu dalam mencari sumber referensi yang relevan dan terpercaya.
Kutipan dari Buku atau Jurnal Ilmiah
“Algebra linear adalah cabang matematika yang mempelajari ruang vektor, transformasi linear, dan sistem persamaan linear.” – Gilbert Strang, “Algebra Linear”
Kutipan di atas menunjukkan definisi dasar dari aljabar linear, yang merupakan topik penting dalam matematika murni.
Pemungkas
Menulis skripsi matematika murni memang menantang, namun sekaligus sangat memuaskan. Anda akan merasakan sensasi menemukan solusi baru untuk masalah matematika yang rumit, dan Anda akan belajar berpikir secara logis dan sistematis. Semoga panduan ini membantu Anda dalam menulis skripsi matematika murni yang memuaskan.