Pernahkah Anda bertanya-tanya bagaimana ilmuwan menggunakan matematika untuk memecahkan masalah kompleks di berbagai bidang? Jurnal Pemodelan Matematika memberikan jawabannya! Jurnal ini merupakan platform ilmiah yang membahas bagaimana matematika digunakan untuk memahami dan memprediksi fenomena di dunia nyata, mulai dari ekonomi dan biologi hingga teknik dan fisika.
Pemodelan matematika merupakan proses membangun model matematika yang merepresentasikan sistem atau proses yang ingin dipelajari. Model ini kemudian dapat digunakan untuk menganalisis data, membuat prediksi, dan menguji hipotesis. Jurnal Pemodelan Matematika meneliti berbagai aspek pemodelan matematika, mulai dari definisi dan ruang lingkup hingga langkah-langkah pengembangan, aplikasi, evaluasi, dan tren terkini.
Pengertian dan Ruang Lingkup Pemodelan Matematika: Jurnal Pemodelan Matematika
Pemodelan matematika merupakan suatu proses yang melibatkan penerapan konsep matematika untuk menggambarkan dan menganalisis sistem atau fenomena dunia nyata. Dalam konteks jurnal ilmiah, pemodelan matematika berfungsi sebagai alat yang ampuh untuk memahami, memprediksi, dan mengendalikan berbagai aspek kompleks dari dunia nyata.
Contoh Penerapan Pemodelan Matematika
Pemodelan matematika memiliki aplikasi luas di berbagai bidang, contohnya:
- Ekonomi: Model matematika digunakan untuk memahami dinamika pasar, memprediksi pertumbuhan ekonomi, dan mengoptimalkan strategi investasi.
- Biologi: Model matematika digunakan untuk mensimulasikan pertumbuhan populasi, penyebaran penyakit, dan interaksi antar spesies.
- Teknik: Model matematika digunakan untuk merancang struktur, menganalisis aliran fluida, dan mengoptimalkan proses produksi.
Jenis-jenis Model Matematika
Berbagai jenis model matematika digunakan dalam jurnal ilmiah, masing-masing dengan karakteristik dan kegunaan yang berbeda. Berikut adalah beberapa jenis model yang umum digunakan:
| Jenis Model | Deskripsi | Contoh Penerapan |
|---|---|---|
| Model Deterministik | Model yang menggunakan persamaan matematika untuk menggambarkan hubungan yang pasti antara variabel-variabel. | Model pertumbuhan penduduk sederhana, model pergerakan benda jatuh bebas. |
| Model Stokastik | Model yang melibatkan variabel acak dan probabilitas untuk menggambarkan fenomena yang tidak pasti. | Model pergerakan harga saham, model simulasi epidemi. |
| Model Linear | Model yang menggunakan hubungan linear antara variabel-variabel. | Model regresi linear, model perencanaan produksi. |
| Model Non-linear | Model yang menggunakan hubungan non-linear antara variabel-variabel. | Model dinamika populasi, model pergerakan planet. |
| Model Diskrit | Model yang menggambarkan sistem dengan menggunakan variabel diskrit (bernilai bulat). | Model jaringan komputer, model antrian. |
| Model Kontinu | Model yang menggambarkan sistem dengan menggunakan variabel kontinu (bernilai real). | Model aliran fluida, model perpindahan panas. |
Langkah-Langkah Pemodelan Matematika
Pemodelan matematika adalah proses yang sistematis dalam menerjemahkan masalah dunia nyata ke dalam bahasa matematika, lalu memecahkannya dengan teknik matematika, dan akhirnya menginterpretasikan hasilnya kembali ke konteks dunia nyata. Pemodelan matematika digunakan dalam berbagai bidang seperti fisika, ekonomi, biologi, dan ilmu komputer. Proses pemodelan matematika melibatkan serangkaian langkah yang terstruktur dan saling terkait, yang membantu peneliti dalam mencapai tujuan penelitiannya. Berikut adalah langkah-langkah utama dalam membangun model matematika untuk penelitian ilmiah.
1. Definisi Masalah
Langkah pertama dalam pemodelan matematika adalah mendefinisikan masalah yang ingin dipecahkan dengan jelas dan terstruktur. Hal ini melibatkan identifikasi variabel-variabel yang relevan, batasan, dan tujuan penelitian. Penting untuk merumuskan masalah secara spesifik dan terukur agar model yang dibangun dapat memberikan solusi yang tepat dan bermakna.
2. Pengumpulan Data
Setelah masalah didefinisikan, langkah selanjutnya adalah mengumpulkan data yang relevan untuk mendukung model yang akan dibangun. Data dapat diperoleh dari berbagai sumber seperti observasi, eksperimen, survei, dan literatur. Kualitas dan kuantitas data sangat penting dalam membangun model yang akurat dan dapat diandalkan.
3. Pemilihan Metode dan Teknik
Pemilihan metode dan teknik pemodelan sangat penting dalam mencapai tujuan penelitian. Metode dan teknik yang dipilih harus sesuai dengan karakteristik masalah, jenis data yang tersedia, dan tujuan penelitian. Beberapa metode pemodelan matematika yang umum digunakan meliputi:
- Model linear
- Model non-linear
- Model stokastik
- Model deterministik
- Model diferensial
- Model optimasi
Dalam memilih metode dan teknik, pertimbangkan faktor-faktor seperti kompleksitas masalah, ketersediaan data, dan tujuan penelitian. Penting untuk memilih metode yang dapat memberikan solusi yang akurat, efisien, dan relevan dengan konteks masalah.
4. Pengembangan Model
Langkah selanjutnya adalah mengembangkan model matematika berdasarkan metode dan teknik yang telah dipilih. Model matematika dapat direpresentasikan dalam bentuk persamaan, grafik, atau algoritma. Model harus konsisten dengan data yang dikumpulkan dan mampu menangkap hubungan yang relevan antara variabel-variabel yang didefinisikan dalam masalah.
5. Validasi Model
Setelah model dikembangkan, perlu dilakukan validasi untuk memastikan bahwa model tersebut dapat diandalkan dan akurat. Validasi dapat dilakukan dengan membandingkan hasil model dengan data observasi atau data yang dikumpulkan secara independen. Jika model tidak sesuai dengan data, perlu dilakukan penyesuaian atau modifikasi model.
6. Simulasi dan Analisis, Jurnal pemodelan matematika
Setelah model divalidasi, langkah selanjutnya adalah melakukan simulasi dan analisis untuk mendapatkan wawasan dan prediksi yang relevan dengan masalah yang dikaji. Simulasi melibatkan menjalankan model dengan berbagai skenario dan parameter untuk mempelajari perilaku sistem yang dimodelkan. Analisis melibatkan interpretasi hasil simulasi untuk mengidentifikasi pola, tren, dan hubungan yang penting.
7. Interpretasi Hasil
Langkah terakhir adalah menginterpretasikan hasil model dan menyimpulkan makna dari hasil simulasi dan analisis. Hasil harus diinterpretasikan dalam konteks masalah yang didefinisikan dan dikaitkan dengan tujuan penelitian. Penting untuk mengkomunikasikan hasil model dengan jelas dan ringkas, serta menyoroti keterbatasan model dan implikasi dari hasil yang diperoleh.
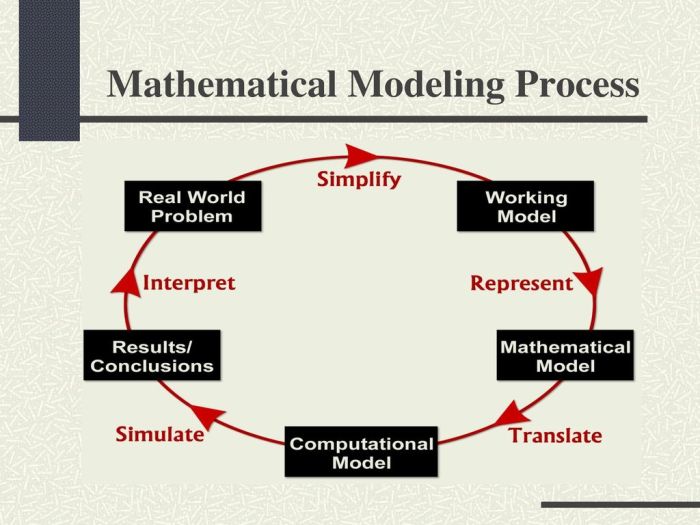
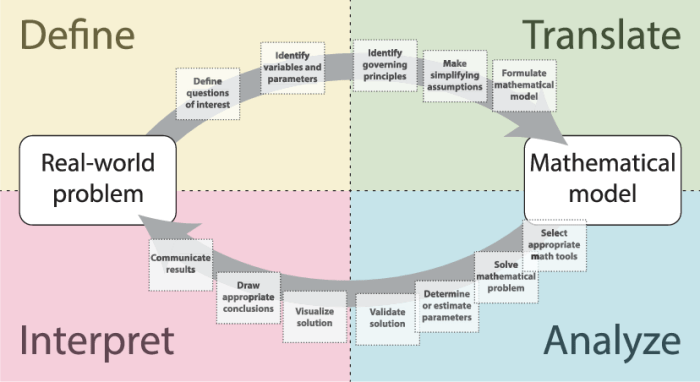
8. Diagram Alur Pemodelan Matematika
Diagram alur di bawah ini menggambarkan proses pemodelan matematika secara keseluruhan, mulai dari definisi masalah hingga interpretasi hasil.

|
Diagram alur ini menunjukkan bahwa proses pemodelan matematika adalah proses yang iteratif dan dinamis, di mana setiap langkah dapat diulang dan dimodifikasi berdasarkan hasil yang diperoleh. Pemodelan matematika merupakan alat yang ampuh untuk memecahkan masalah dunia nyata dan menghasilkan wawasan yang berharga untuk mendukung pengambilan keputusan yang lebih baik.
Aplikasi Pemodelan Matematika dalam Jurnal
Pemodelan matematika merupakan alat yang ampuh dalam memecahkan berbagai masalah ilmiah. Dalam berbagai jurnal, pemodelan matematika digunakan untuk menganalisis data, membangun teori, dan memprediksi hasil. Penggunaan pemodelan matematika dalam jurnal memungkinkan para peneliti untuk memahami fenomena kompleks, menguji hipotesis, dan mengembangkan solusi inovatif.
Contoh Jurnal yang Menggunakan Pemodelan Matematika
Pemodelan matematika digunakan dalam berbagai bidang ilmiah, seperti fisika, kimia, biologi, ekonomi, dan ilmu komputer. Berikut beberapa contoh jurnal yang menggunakan pemodelan matematika untuk memecahkan masalah ilmiah:
- Jurnal Fisika: Model matematika digunakan untuk memprediksi pergerakan planet, perilaku partikel subatomik, dan dinamika fluida. Contohnya, model matematika yang digunakan untuk memprediksi pergerakan planet di tata surya kita membantu para astronom memahami hukum gravitasi dan pergerakan benda langit.
- Jurnal Biologi: Model matematika digunakan untuk memahami dinamika populasi, penyebaran penyakit, dan interaksi antar spesies. Contohnya, model matematika digunakan untuk memprediksi penyebaran virus seperti COVID-19, membantu para ilmuwan memahami pola penyebaran dan merumuskan strategi pengendalian.
- Jurnal Ekonomi: Model matematika digunakan untuk menganalisis pasar keuangan, memprediksi pertumbuhan ekonomi, dan merancang kebijakan ekonomi. Contohnya, model matematika digunakan untuk memprediksi nilai tukar mata uang, membantu para ekonom memahami faktor-faktor yang memengaruhi nilai tukar dan merumuskan strategi investasi.
Jenis Data yang Digunakan dalam Pemodelan Matematika
Data yang digunakan dalam pemodelan matematika dapat berupa data kualitatif maupun kuantitatif. Data kualitatif biasanya digunakan untuk menggambarkan karakteristik atau sifat suatu objek, sementara data kuantitatif digunakan untuk mengukur besaran atau nilai suatu objek.
- Data Kualitatif: Data kualitatif dapat berupa teks, gambar, atau video yang menggambarkan suatu fenomena. Contohnya, dalam penelitian tentang perilaku konsumen, data kualitatif dapat berupa teks dari survei atau wawancara yang menggambarkan preferensi konsumen terhadap produk tertentu.
- Data Kuantitatif: Data kuantitatif dapat berupa angka atau nilai yang dapat diukur. Contohnya, dalam penelitian tentang efektivitas obat, data kuantitatif dapat berupa data tentang dosis obat, waktu pemberian obat, dan respons pasien terhadap obat.
Ilustrasi Penggunaan Model Matematika
Sebagai contoh, mari kita perhatikan model matematika yang digunakan untuk memprediksi penyebaran penyakit. Model ini menggunakan data kuantitatif, seperti jumlah orang yang terinfeksi, tingkat kontak antar individu, dan tingkat penularan penyakit. Model ini kemudian dapat digunakan untuk memprediksi jumlah orang yang akan terinfeksi di masa depan, membantu para ilmuwan memahami pola penyebaran penyakit dan merumuskan strategi pengendalian.
Model matematika untuk memprediksi penyebaran penyakit biasanya menggunakan persamaan diferensial, yang menggambarkan hubungan antara variabel-variabel yang memengaruhi penyebaran penyakit.
Model matematika ini kemudian dapat digunakan untuk menganalisis data dan menarik kesimpulan. Misalnya, model ini dapat menunjukkan bahwa peningkatan tingkat kontak antar individu akan meningkatkan jumlah orang yang terinfeksi. Kesimpulan ini kemudian dapat digunakan untuk merumuskan strategi pengendalian, seperti menerapkan kebijakan pembatasan sosial.
Evaluasi dan Validasi Model Matematika

Setelah model matematika dibangun, langkah selanjutnya adalah mengevaluasi dan memvalidasi keakuratan dan keandalannya. Proses ini sangat penting untuk memastikan bahwa model tersebut dapat diandalkan untuk memprediksi hasil yang akurat dan dapat diterapkan pada situasi nyata. Evaluasi dan validasi melibatkan analisis model dan membandingkannya dengan data empiris untuk menilai kemampuannya dalam merepresentasikan sistem atau fenomena yang dimodelkan.
Metode Evaluasi Akurasi dan Keandalan Model
Ada beberapa metode yang dapat digunakan untuk mengevaluasi akurasi dan keandalan model matematika. Metode-metode ini memungkinkan kita untuk menilai seberapa baik model tersebut memprediksi hasil yang benar dan seberapa sensitifnya terhadap perubahan dalam data input. Beberapa metode yang umum digunakan meliputi:
- Error kuadrat rata-rata (MSE): MSE mengukur rata-rata kuadrat selisih antara nilai prediksi dan nilai aktual. Nilai MSE yang rendah menunjukkan model yang akurat.
- R-squared (R2): R2 mengukur proporsi varians data yang dijelaskan oleh model. Nilai R2 yang tinggi menunjukkan bahwa model dapat menjelaskan sebagian besar varians data.
- Analisis Sensitivitas: Analisis sensitivitas mengkaji bagaimana perubahan dalam parameter input memengaruhi hasil prediksi model. Metode ini membantu dalam memahami seberapa sensitif model terhadap perubahan data input.
- Cross-validation: Cross-validation melibatkan pemisahan data menjadi beberapa subset, dan kemudian melatih dan mengevaluasi model pada subset yang berbeda. Metode ini membantu dalam menghindari overfitting, di mana model terlalu cocok dengan data pelatihan dan tidak dapat digeneralisasikan dengan baik pada data baru.
Validasi Model Berdasarkan Data Empiris
Validasi model matematika melibatkan membandingkan prediksi model dengan data empiris yang diperoleh dari sistem atau fenomena yang dimodelkan. Tujuannya adalah untuk menguji seberapa baik model tersebut dapat memprediksi hasil yang benar dalam situasi nyata. Beberapa metode validasi meliputi:
- Verifikasi Data: Verifikasi data melibatkan pemeriksaan data empiris untuk memastikan keakuratan dan konsistensinya. Hal ini penting untuk memastikan bahwa data yang digunakan untuk validasi model valid dan dapat diandalkan.
- Uji Prediksi: Uji prediksi melibatkan menggunakan model untuk memprediksi hasil pada data empiris yang belum pernah digunakan untuk melatih model. Hal ini membantu dalam menilai kemampuan model untuk memprediksi hasil yang benar pada data baru.
- Uji Sensitivitas: Uji sensitivitas melibatkan mengubah parameter input model dan mengamati bagaimana perubahan ini memengaruhi hasil prediksi. Hal ini membantu dalam memahami seberapa sensitif model terhadap perubahan dalam data input.
Perbandingan Metode Evaluasi dan Validasi
| Metode | Tujuan | Keuntungan | Kerugian |
|---|---|---|---|
| MSE | Mengukur akurasi model | Mudah dihitung dan diinterpretasikan | Sensitif terhadap outlier |
| R2 | Mengukur proporsi varians data yang dijelaskan oleh model | Mudah diinterpretasikan | Tidak memberikan informasi tentang kecocokan model |
| Analisis Sensitivitas | Mengkaji sensitivitas model terhadap perubahan data input | Membantu dalam memahami perilaku model | Membutuhkan analisis yang kompleks |
| Cross-validation | Mencegah overfitting | Meningkatkan generalisasi model | Membutuhkan banyak data |
| Verifikasi Data | Memastikan keakuratan data empiris | Meningkatkan keandalan validasi model | Membutuhkan waktu dan usaha |
| Uji Prediksi | Menilai kemampuan model untuk memprediksi hasil yang benar pada data baru | Membantu dalam menilai generalisasi model | Membutuhkan data empiris yang baru |
| Uji Sensitivitas | Mengkaji sensitivitas model terhadap perubahan data input | Membantu dalam memahami perilaku model | Membutuhkan analisis yang kompleks |
Tren dan Tantangan Pemodelan Matematika
Pemodelan matematika telah menjadi alat yang tak ternilai dalam berbagai bidang ilmiah, dari fisika dan biologi hingga ekonomi dan ilmu komputer. Dalam beberapa tahun terakhir, telah terjadi kemajuan signifikan dalam pengembangan dan aplikasi pemodelan matematika, yang mengarah pada pemahaman yang lebih dalam tentang fenomena kompleks dan kemampuan untuk membuat prediksi yang lebih akurat. Artikel ini akan membahas tren terkini dalam pemodelan matematika, mengidentifikasi tantangan dan keterbatasan yang terkait dengan penerapannya, dan menyoroti strategi untuk mengatasi tantangan tersebut dan meningkatkan kualitas pemodelan matematika.
Tren dalam Pemodelan Matematika
Beberapa tren menonjol dalam pengembangan dan aplikasi pemodelan matematika. Berikut ini adalah beberapa contoh yang paling signifikan:
- Peningkatan kompleksitas model: Model matematika menjadi semakin kompleks untuk menangkap kompleksitas sistem dunia nyata. Model-model ini sering kali melibatkan sejumlah besar variabel, persamaan, dan parameter, yang membutuhkan pendekatan komputasi canggih untuk diselesaikan dan dianalisis.
- Peningkatan penggunaan data: Data besar dan kemampuan komputasi yang meningkat telah memungkinkan pengembangan model data-driven yang memanfaatkan kumpulan data yang besar untuk membuat prediksi dan wawasan. Teknik pembelajaran mesin dan kecerdasan buatan memainkan peran penting dalam pendekatan ini.
- Peningkatan interdisipliner: Pemodelan matematika semakin banyak digunakan dalam bidang interdisipliner, seperti biologi komputasi, ilmu saraf komputasi, dan ilmu data. Kolaborasi antara ahli matematika, ilmuwan komputer, dan peneliti di berbagai disiplin ilmu lain telah menghasilkan model-model inovatif yang memberikan wawasan baru tentang fenomena kompleks.
- Pemodelan stokastik dan probabilistik: Pemodelan stokastik dan probabilistik menjadi semakin penting dalam menangani ketidakpastian dan variabilitas dalam sistem dunia nyata. Model-model ini memungkinkan para peneliti untuk memperkirakan kemungkinan hasil dan membuat keputusan berdasarkan informasi yang tidak lengkap.
Tantangan dalam Pemodelan Matematika
Meskipun kemajuan yang signifikan dalam pemodelan matematika, beberapa tantangan dan keterbatasan tetap ada. Tantangan-tantangan ini dapat membatasi akurasi, reliabilitas, dan interpretasi model:
- Kompleksitas sistem dunia nyata: Sistem dunia nyata sering kali sangat kompleks dan sulit dimodelkan dengan akurasi penuh. Penyederhanaan dan asumsi diperlukan untuk membuat model yang dapat ditangani, tetapi ini dapat menyebabkan hilangnya informasi penting dan kesalahan dalam prediksi.
- Keterbatasan data: Model data-driven bergantung pada data yang memadai dan berkualitas tinggi. Ketersediaan data yang terbatas, kualitas data yang buruk, atau bias dalam data dapat membatasi akurasi dan generalisasi model.
- Validasi dan verifikasi model: Validasi dan verifikasi model adalah langkah penting untuk memastikan bahwa model tersebut akurat, andal, dan sesuai untuk tujuan yang dimaksudkan. Ini dapat menjadi proses yang menantang, terutama untuk model kompleks.
- Interpretasi dan komunikasi: Model matematika dapat menghasilkan hasil yang kompleks dan sulit diinterpretasikan. Mengaitkan hasil model dengan pemahaman dunia nyata dan mengkomunikasikannya secara efektif kepada audiens non-teknis dapat menjadi tantangan.
Strategi untuk Mengatasi Tantangan
Untuk mengatasi tantangan dan meningkatkan kualitas pemodelan matematika, beberapa strategi dapat diterapkan:
- Peningkatan kolaborasi interdisipliner: Kolaborasi antara ahli matematika, ilmuwan komputer, dan peneliti di berbagai disiplin ilmu dapat membantu mengembangkan model yang lebih komprehensif dan realistis.
- Pengembangan teknik pemodelan yang lebih canggih: Pengembangan metode dan algoritma pemodelan baru, seperti pembelajaran mesin, jaringan saraf, dan pemodelan stokastik, dapat membantu mengatasi kompleksitas sistem dunia nyata.
- Peningkatan kualitas dan kuantitas data: Upaya untuk mengumpulkan, membersihkan, dan menganalisis data yang berkualitas tinggi sangat penting untuk meningkatkan akurasi dan generalisasi model data-driven.
- Pengembangan metode validasi dan verifikasi yang lebih kuat: Pengembangan metode validasi dan verifikasi model yang lebih kuat dapat membantu memastikan bahwa model tersebut akurat, andal, dan sesuai untuk tujuan yang dimaksudkan.
- Peningkatan komunikasi dan interpretasi: Upaya untuk mengembangkan metode yang lebih efektif untuk menginterpretasikan hasil model dan mengkomunikasikannya kepada audiens non-teknis dapat meningkatkan penerimaan dan dampak pemodelan matematika.
Ringkasan Penutup
Jurnal Pemodelan Matematika merupakan sumber penting bagi para peneliti, mahasiswa, dan praktisi yang ingin memahami dan mengaplikasikan matematika dalam penelitian ilmiah. Dengan mempelajari jurnal ini, kita dapat memperoleh wawasan yang lebih dalam tentang bagaimana matematika dapat digunakan untuk memecahkan masalah kompleks dan memajukan berbagai bidang ilmu pengetahuan.






