Menjelajahi dunia matematika kelas 11 semester 2 bisa jadi menantang, namun dengan bantuan materi dalam format PDF, proses belajar bisa menjadi lebih mudah dan menyenangkan. Bayangkan, semua materi yang kamu butuhkan, mulai dari konsep dasar hingga contoh soal, tersedia dalam genggamanmu. Dengan format PDF, kamu dapat mengakses materi kapan saja dan di mana saja, tanpa perlu repot membawa buku tebal. Materi matematika kelas 11 semester 2 PDF menawarkan berbagai keunggulan, seperti kemudahan akses, portabilitas, dan fitur-fitur tambahan yang dapat membantu kamu memahami konsep dengan lebih baik.
Materi matematika kelas 11 semester 2 PDF mencakup berbagai topik penting, seperti kalkulus, geometri analitik, dan peluang. Setiap topik disajikan secara detail, lengkap dengan contoh soal dan langkah penyelesaiannya. Selain itu, materi ini juga dilengkapi dengan ilustrasi yang menarik untuk mempermudah pemahaman konsep.
Materi Matematika Kelas 11 Semester 2: Materi Matematika Kelas 11 Semester 2 Pdf

Matematika kelas 11 semester 2 merupakan lanjutan dari materi semester sebelumnya. Di semester ini, kamu akan mempelajari konsep-konsep matematika yang lebih kompleks dan aplikatif, yang akan mempersiapkanmu untuk menghadapi tantangan di perguruan tinggi. Materi yang dipelajari meliputi:
Limit Fungsi
Limit fungsi merupakan konsep dasar dalam kalkulus yang mempelajari perilaku suatu fungsi saat variabelnya mendekati suatu nilai tertentu. Konsep ini penting untuk memahami konsep turunan dan integral, yang merupakan dasar dari banyak aplikasi matematika dalam berbagai bidang.
- Definisi limit fungsi
- Sifat-sifat limit fungsi
- Menghitung limit fungsi aljabar
- Menghitung limit fungsi trigonometri
- Limit fungsi tak hingga
Contoh soal: Tentukan limit fungsi f(x) = (x^2 – 4) / (x – 2) saat x mendekati 2.
Penyelesaian:
Limit fungsi f(x) saat x mendekati 2 dapat dihitung dengan cara mensubstitusikan nilai x = 2 ke dalam fungsi f(x). Namun, hal ini akan menghasilkan bentuk tak tentu 0/0. Untuk mengatasi hal ini, kita dapat memfaktorkan fungsi f(x) terlebih dahulu.
f(x) = (x^2 – 4) / (x – 2) = (x + 2)(x – 2) / (x – 2) = x + 2
Sekarang, kita dapat mensubstitusikan nilai x = 2 ke dalam fungsi f(x) dan mendapatkan hasil limit fungsi tersebut.
lim x->2 f(x) = lim x->2 (x + 2) = 2 + 2 = 4
Jadi, limit fungsi f(x) = (x^2 – 4) / (x – 2) saat x mendekati 2 adalah 4.
Contoh penerapan limit fungsi dalam kehidupan sehari-hari adalah dalam analisis data pertumbuhan ekonomi. Data pertumbuhan ekonomi dapat dimodelkan dengan fungsi matematika, dan limit fungsi dapat digunakan untuk memprediksi pertumbuhan ekonomi di masa depan.
Ilustrasi: Ilustrasi limit fungsi dapat digambarkan dengan grafik fungsi yang mendekati suatu titik tertentu. Grafik tersebut akan menunjukkan bahwa nilai fungsi semakin mendekati suatu nilai tertentu saat variabelnya semakin mendekati titik tertentu.
Turunan Fungsi
Turunan fungsi merupakan konsep penting dalam kalkulus yang mempelajari laju perubahan suatu fungsi terhadap perubahan variabelnya. Turunan fungsi memiliki banyak aplikasi dalam berbagai bidang, seperti fisika, ekonomi, dan teknik.
- Definisi turunan fungsi
- Rumus turunan fungsi dasar
- Aturan turunan fungsi
- Aplikasi turunan fungsi
Contoh soal: Tentukan turunan fungsi f(x) = x^3 + 2x^2 – 5x + 1.
Penyelesaian:
Turunan fungsi f(x) dapat dihitung dengan menggunakan rumus turunan fungsi dasar.
f'(x) = 3x^2 + 4x – 5
Jadi, turunan fungsi f(x) = x^3 + 2x^2 – 5x + 1 adalah f'(x) = 3x^2 + 4x – 5.
Contoh penerapan turunan fungsi dalam kehidupan sehari-hari adalah dalam perhitungan kecepatan dan percepatan benda. Kecepatan benda dapat dihitung dengan menurunkan fungsi posisi benda terhadap waktu, dan percepatan benda dapat dihitung dengan menurunkan fungsi kecepatan benda terhadap waktu.
Ilustrasi: Ilustrasi turunan fungsi dapat digambarkan dengan grafik fungsi yang menunjukkan laju perubahan fungsi terhadap perubahan variabelnya. Grafik tersebut akan menunjukkan kemiringan garis singgung pada kurva fungsi, yang mewakili laju perubahan fungsi pada titik tertentu.
Integral Fungsi
Integral fungsi merupakan konsep penting dalam kalkulus yang mempelajari luas daerah di bawah kurva fungsi. Integral fungsi memiliki banyak aplikasi dalam berbagai bidang, seperti fisika, ekonomi, dan teknik.
- Definisi integral fungsi
- Rumus integral fungsi dasar
- Teknik integrasi
- Aplikasi integral fungsi
Contoh soal: Tentukan integral fungsi f(x) = 2x + 1.
Penyelesaian:
Integral fungsi f(x) dapat dihitung dengan menggunakan rumus integral fungsi dasar.
∫f(x) dx = ∫(2x + 1) dx = x^2 + x + C
Jadi, integral fungsi f(x) = 2x + 1 adalah x^2 + x + C, dengan C adalah konstanta integrasi.
Contoh penerapan integral fungsi dalam kehidupan sehari-hari adalah dalam perhitungan volume benda putar. Volume benda putar dapat dihitung dengan mengintegrasikan luas penampang benda putar terhadap sumbu rotasi.
Ilustrasi: Ilustrasi integral fungsi dapat digambarkan dengan grafik fungsi yang menunjukkan luas daerah di bawah kurva fungsi. Grafik tersebut akan menunjukkan luas daerah yang dibatasi oleh kurva fungsi, sumbu x, dan dua garis vertikal.
Statistika
Statistika merupakan cabang matematika yang mempelajari cara mengumpulkan, menganalisis, menginterpretasikan, dan menyajikan data. Statistika memiliki banyak aplikasi dalam berbagai bidang, seperti bisnis, kesehatan, dan sosial.
- Pengukuran data
- Probabilitas
- Distribusi probabilitas
- Uji hipotesis
- Regresi linier
Contoh soal: Sebuah perusahaan ingin mengetahui rata-rata tinggi badan karyawannya. Mereka mengambil sampel 50 karyawan dan mendapatkan rata-rata tinggi badan 170 cm. Hitunglah rata-rata tinggi badan seluruh karyawan di perusahaan tersebut.
Penyelesaian:
Rata-rata tinggi badan seluruh karyawan di perusahaan tersebut dapat dihitung dengan menggunakan rumus rata-rata sampel.
Rata-rata sampel = Σxi / n
Dimana Σxi adalah jumlah tinggi badan seluruh karyawan dalam sampel, dan n adalah jumlah karyawan dalam sampel.
Rata-rata sampel = 170 cm
Jumlah karyawan dalam sampel = 50
Maka, rata-rata tinggi badan seluruh karyawan di perusahaan tersebut adalah:
Rata-rata populasi = Rata-rata sampel = 170 cm
Contoh penerapan statistika dalam kehidupan sehari-hari adalah dalam analisis data penjualan produk. Data penjualan produk dapat dianalisis dengan menggunakan statistika untuk mengetahui pola penjualan, tren penjualan, dan faktor-faktor yang mempengaruhi penjualan.
Ilustrasi: Ilustrasi statistika dapat digambarkan dengan diagram batang, diagram lingkaran, atau histogram yang menunjukkan distribusi data. Diagram tersebut akan menunjukkan frekuensi data pada setiap kategori atau interval.
Peluang
Peluang merupakan konsep matematika yang mempelajari kemungkinan terjadinya suatu peristiwa. Peluang memiliki banyak aplikasi dalam berbagai bidang, seperti permainan, asuransi, dan keuangan.
- Definisi peluang
- Jenis-jenis peluang
- Rumus peluang
- Teorema peluang
Contoh soal: Sebuah dadu dilempar sekali. Berapakah peluang munculnya mata dadu 5?
Penyelesaian:
Peluang munculnya mata dadu 5 dapat dihitung dengan menggunakan rumus peluang.
Peluang = Jumlah kejadian yang diinginkan / Jumlah kejadian yang mungkin
Jumlah kejadian yang diinginkan = 1 (munculnya mata dadu 5)
Jumlah kejadian yang mungkin = 6 (munculnya mata dadu 1, 2, 3, 4, 5, atau 6)
Maka, peluang munculnya mata dadu 5 adalah:
Peluang = 1 / 6
Contoh penerapan peluang dalam kehidupan sehari-hari adalah dalam permainan judi. Peluang dapat digunakan untuk menghitung kemungkinan menang atau kalah dalam permainan judi.
Ilustrasi: Ilustrasi peluang dapat digambarkan dengan diagram pohon yang menunjukkan semua kemungkinan kejadian. Diagram pohon akan menunjukkan semua kemungkinan hasil dari suatu peristiwa.
Trigonometri
Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sudut dan sisi dalam segitiga siku-siku. Trigonometri memiliki banyak aplikasi dalam berbagai bidang, seperti navigasi, astronomi, dan teknik.
- Sudut dan ukuran sudut
- Fungsi trigonometri
- Identitas trigonometri
- Persamaan trigonometri
Contoh soal: Tentukan nilai sin 30 derajat.
Penyelesaian:
Nilai sin 30 derajat dapat dihitung dengan menggunakan tabel trigonometri atau dengan menggunakan rumus sin 30 derajat = 1/2.
Jadi, nilai sin 30 derajat adalah 1/2.
Contoh penerapan trigonometri dalam kehidupan sehari-hari adalah dalam navigasi. Trigonometri dapat digunakan untuk menentukan posisi kapal atau pesawat terbang.
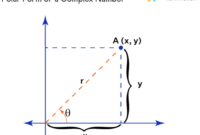
Ilustrasi: Ilustrasi trigonometri dapat digambarkan dengan segitiga siku-siku yang menunjukkan hubungan antara sudut dan sisi. Ilustrasi tersebut akan menunjukkan nilai sinus, cosinus, dan tangen dari sudut tertentu.
Logaritma
Logaritma merupakan fungsi invers dari eksponen. Logaritma memiliki banyak aplikasi dalam berbagai bidang, seperti fisika, kimia, dan ekonomi.
- Definisi logaritma
- Sifat-sifat logaritma
- Persamaan logaritma
- Pertidaksamaan logaritma
Contoh soal: Tentukan nilai log 100 dengan basis 10.
Penyelesaian:
Nilai log 100 dengan basis 10 adalah 2, karena 10^2 = 100.
Jadi, log 100 dengan basis 10 adalah 2.
Contoh penerapan logaritma dalam kehidupan sehari-hari adalah dalam perhitungan skala Richter untuk gempa bumi. Skala Richter menggunakan logaritma untuk mengukur kekuatan gempa bumi.
Ilustrasi: Ilustrasi logaritma dapat digambarkan dengan grafik fungsi logaritma yang menunjukkan hubungan antara nilai logaritma dan nilai eksponen.
Geometri Vektor
Geometri vektor merupakan cabang matematika yang mempelajari vektor, yang merupakan besaran yang memiliki nilai dan arah. Geometri vektor memiliki banyak aplikasi dalam berbagai bidang, seperti fisika, teknik, dan komputer grafis.
- Definisi vektor
- Operasi vektor
- Aplikasi vektor
Contoh soal: Diketahui vektor a = (2, 3) dan vektor b = (1, -1). Tentukan hasil penjumlahan vektor a + b.
Penyelesaian:
Hasil penjumlahan vektor a + b dapat dihitung dengan menjumlahkan komponen-komponen vektor a dan b.
a + b = (2, 3) + (1, -1) = (2 + 1, 3 – 1) = (3, 2)
Jadi, hasil penjumlahan vektor a + b adalah (3, 2).
Contoh penerapan geometri vektor dalam kehidupan sehari-hari adalah dalam navigasi. Vektor dapat digunakan untuk menentukan arah dan jarak perjalanan.
Ilustrasi: Ilustrasi geometri vektor dapat digambarkan dengan diagram vektor yang menunjukkan arah dan besar vektor. Diagram tersebut akan menunjukkan operasi vektor seperti penjumlahan, pengurangan, perkalian skalar, dan perkalian vektor.
Barisan dan Deret
Barisan dan deret merupakan konsep matematika yang mempelajari urutan bilangan yang memiliki pola tertentu. Barisan dan deret memiliki banyak aplikasi dalam berbagai bidang, seperti keuangan, fisika, dan komputer.
- Definisi barisan dan deret
- Jenis-jenis barisan dan deret
- Rumus barisan dan deret
- Aplikasi barisan dan deret
Contoh soal: Tentukan suku ke-5 dari barisan aritmatika 2, 5, 8, 11, … .
Penyelesaian:
Suku ke-5 dari barisan aritmatika dapat dihitung dengan menggunakan rumus suku ke-n barisan aritmatika.
an = a1 + (n – 1)d
Dimana an adalah suku ke-n, a1 adalah suku pertama, dan d adalah beda.
a1 = 2
d = 5 – 2 = 3
n = 5
Maka, suku ke-5 dari barisan aritmatika adalah:
a5 = 2 + (5 – 1)3 = 2 + 12 = 14
Contoh penerapan barisan dan deret dalam kehidupan sehari-hari adalah dalam perhitungan bunga majemuk. Bunga majemuk dapat dihitung dengan menggunakan rumus deret geometri.
Ilustrasi: Ilustrasi barisan dan deret dapat digambarkan dengan diagram yang menunjukkan pola bilangan dalam barisan atau deret. Diagram tersebut akan menunjukkan hubungan antara suku-suku dalam barisan atau deret.
Matriks
Matriks merupakan susunan bilangan yang disusun dalam baris dan kolom. Matriks memiliki banyak aplikasi dalam berbagai bidang, seperti ekonomi, teknik, dan komputer grafis.
- Definisi matriks
- Operasi matriks
- Determinan matriks
- Invers matriks
- Sistem persamaan linear
Contoh soal: Diketahui matriks A = [2 1; 3 4] dan matriks B = [1 2; 3 4]. Tentukan hasil perkalian matriks A x B.
Penyelesaian:
Hasil perkalian matriks A x B dapat dihitung dengan mengalikan setiap baris matriks A dengan setiap kolom matriks B.
A x B = [2 1; 3 4] x [1 2; 3 4] = [(2 x 1) + (1 x 3) (2 x 2) + (1 x 4); (3 x 1) + (4 x 3) (3 x 2) + (4 x 4)] = [5 8; 15 22]
Jadi, hasil perkalian matriks A x B adalah [5 8; 15 22].
Contoh penerapan matriks dalam kehidupan sehari-hari adalah dalam pemodelan ekonomi. Matriks dapat digunakan untuk memodelkan hubungan antara berbagai variabel ekonomi.
Ilustrasi: Ilustrasi matriks dapat digambarkan dengan tabel yang menunjukkan susunan bilangan dalam matriks. Tabel tersebut akan menunjukkan baris dan kolom dalam matriks.
Materi Matematika Kelas 11 Semester 2 PDF
Belajar matematika di kelas 11 semester 2 bisa jadi menantang, tapi jangan khawatir! Materi-materi yang rumit dan abstrak bisa dipelajari dengan lebih mudah dengan memanfaatkan sumber belajar yang tepat, salah satunya adalah materi matematika kelas 11 semester 2 dalam format PDF. Format PDF memiliki banyak kelebihan yang membuatnya ideal untuk mempelajari matematika, mulai dari kemudahan akses hingga kemampuan untuk menyimpan dan berbagi file.
Format PDF sebagai Media Penyampaian Materi Matematika, Materi matematika kelas 11 semester 2 pdf
Format PDF (Portable Document Format) telah menjadi standar de facto untuk berbagi dokumen digital karena beberapa alasan. Format ini memiliki beberapa keunggulan yang membuatnya cocok untuk materi pembelajaran matematika, yaitu:
- Kemudahan Akses: File PDF dapat diakses di berbagai perangkat, termasuk komputer, tablet, dan smartphone, tanpa perlu menginstal aplikasi khusus. Hal ini memungkinkan siswa untuk mengakses materi belajar kapan saja dan di mana saja.
- Kejelasan dan Ketelitian: Format PDF mampu mempertahankan format asli dokumen, termasuk gambar, grafik, dan persamaan matematika, sehingga konten materi tetap jelas dan mudah dipahami.
- Kemudahan Cetak: Materi dalam format PDF dapat dicetak dengan mudah, sehingga siswa dapat memiliki salinan fisik yang bisa mereka tulis dan tandai saat belajar.
- Keamanan: File PDF dapat diproteksi dengan kata sandi, sehingga hanya pengguna yang berwenang yang dapat mengaksesnya. Hal ini membantu menjaga keamanan dan integritas materi belajar.
Platform Online yang Menyediakan Materi Matematika Kelas 11 Semester 2 PDF
Banyak platform online yang menyediakan materi matematika kelas 11 semester 2 dalam format PDF. Berikut ini adalah beberapa contoh platform online yang populer, beserta kelebihan dan kekurangannya:
| Platform | Kelebihan | Kekurangan |
|---|---|---|
| [Nama Platform 1] | [Kelebihan 1], [Kelebihan 2], [Kelebihan 3] | [Kekurangan 1], [Kekurangan 2], [Kekurangan 3] |
| [Nama Platform 2] | [Kelebihan 1], [Kelebihan 2], [Kelebihan 3] | [Kekurangan 1], [Kekurangan 2], [Kekurangan 3] |
| [Nama Platform 3] | [Kelebihan 1], [Kelebihan 2], [Kelebihan 3] | [Kekurangan 1], [Kekurangan 2], [Kekurangan 3] |
Tips dan Trik Mengunduh dan Mengakses Materi Matematika PDF
Berikut ini beberapa tips dan trik yang dapat membantu kamu dalam mengunduh dan mengakses materi matematika kelas 11 semester 2 PDF:
- Pilih Platform yang Terpercaya: Pastikan platform yang kamu gunakan untuk mengunduh materi PDF terpercaya dan memiliki reputasi baik. Hindari platform yang tidak jelas atau mencurigakan.
- Perhatikan Judul dan Deskripsi File: Sebelum mengunduh, perhatikan judul dan deskripsi file PDF. Pastikan file tersebut sesuai dengan materi yang kamu butuhkan.
- Unduh dari Situs Resmi: Jika memungkinkan, unduh materi PDF dari situs resmi sekolah, lembaga pendidikan, atau penerbit buku pelajaran. Situs resmi biasanya memiliki materi yang akurat dan terpercaya.
- Gunakan Perangkat Lunak Antivirus: Pastikan kamu menggunakan perangkat lunak antivirus yang terupdate untuk melindungi perangkatmu dari malware atau virus yang mungkin tersembunyi dalam file PDF yang diunduh.
- Simpan File PDF di Tempat yang Aman: Simpan file PDF yang diunduh di folder yang mudah diakses, sehingga kamu dapat menemukannya dengan mudah saat dibutuhkan.
Memanfaatkan Materi Matematika PDF untuk Belajar Efektif
Materi matematika kelas 11 semester 2 dalam format PDF dapat menjadi alat belajar yang efektif jika kamu memanfaatkannya dengan benar. Berikut beberapa tips untuk belajar secara efektif dengan materi PDF:
- Baca dengan Cermat: Baca materi PDF dengan cermat dan pahami konsep-konsep yang dijelaskan. Jangan ragu untuk membaca ulang bagian yang sulit dipahami.
- Tandai Poin Penting: Tandai poin-poin penting, rumus, dan contoh soal dalam materi PDF. Hal ini akan membantu kamu mengingat informasi penting saat belajar.
- Buat Catatan: Buat catatan singkat saat membaca materi PDF. Catatan akan membantu kamu memahami dan mengingat materi dengan lebih baik.
- Kerjakan Soal Latihan: Kerjakan soal latihan yang tersedia dalam materi PDF. Soal latihan akan membantu kamu menguji pemahaman dan mengasah kemampuan menyelesaikan masalah.
- Manfaatkan Fitur Pencarian: Manfaatkan fitur pencarian dalam perangkat lunak PDF reader untuk menemukan informasi spesifik dalam materi PDF.
Keunggulan Materi Matematika Kelas 11 Semester 2 PDF

Materi matematika kelas 11 semester 2 dalam format PDF memiliki sejumlah keunggulan yang membuatnya menjadi pilihan yang ideal untuk belajar. Format PDF memungkinkan akses mudah, portabilitas, dan fitur tambahan yang dapat membantu siswa memahami konsep matematika dengan lebih baik.
Kemudahan Akses
Materi matematika kelas 11 semester 2 PDF dapat diakses dengan mudah melalui berbagai perangkat, seperti komputer, laptop, tablet, dan smartphone. Siswa dapat mengunduh dan menyimpan materi ini di perangkat mereka sehingga dapat diakses kapan saja dan di mana saja.
Portabilitas
Format PDF memungkinkan siswa membawa materi matematika kelas 11 semester 2 ke mana pun mereka pergi. Hal ini sangat berguna bagi siswa yang ingin belajar di luar kelas, seperti di perpustakaan, di rumah, atau saat bepergian.
Fitur Tambahan
Materi matematika kelas 11 semester 2 PDF seringkali dilengkapi dengan fitur tambahan yang dapat membantu siswa dalam memahami konsep. Fitur-fitur ini dapat berupa:
- Tautan ke sumber daya tambahan, seperti video penjelasan, simulasi, atau latihan interaktif.
- Fungsi pencarian untuk menemukan informasi yang spesifik dengan cepat.
- Kemampuan untuk menandai bagian penting dari materi.
- Kemampuan untuk menambahkan catatan dan komentar pada materi.
Membantu Pemahaman Konsep
Materi matematika kelas 11 semester 2 PDF dapat membantu siswa dalam memahami konsep dengan lebih baik melalui:
- Penyajian materi yang terstruktur dan mudah dipahami.
- Ilustrasi dan diagram yang membantu memvisualisasikan konsep.
- Contoh soal dan penyelesaian yang memberikan panduan untuk memahami konsep.
Meningkatkan Hasil Belajar
Materi matematika kelas 11 semester 2 PDF dapat meningkatkan hasil belajar siswa dengan:
- Membantu siswa untuk belajar secara mandiri dan fleksibel.
- Memberikan akses ke materi yang lebih lengkap dan terperinci.
- Memfasilitasi latihan dan evaluasi diri secara teratur.
Ilustrasi Penggunaan
Materi matematika kelas 11 semester 2 PDF dapat digunakan dalam berbagai situasi, seperti:
- Siswa dapat mengunduh materi PDF untuk mempelajari materi di rumah sebelum kelas.
- Guru dapat menggunakan materi PDF untuk memberikan tugas tambahan kepada siswa.
- Siswa dapat menggunakan materi PDF untuk mempersiapkan diri untuk ujian.
- Siswa dapat menggunakan materi PDF untuk mereview materi yang telah dipelajari.
Tips Belajar dengan Materi Matematika Kelas 11 Semester 2 PDF

Belajar matematika bisa menjadi tantangan, tetapi dengan memanfaatkan materi PDF kelas 11 semester 2 secara efektif, kamu dapat meningkatkan pemahaman dan meraih hasil yang lebih baik. Materi PDF, dengan berbagai fitur interaktifnya, bisa menjadi alat belajar yang hebat jika kamu tahu cara memanfaatkannya dengan benar. Artikel ini akan membahas beberapa tips dan trik yang bisa kamu gunakan untuk belajar matematika dengan materi PDF kelas 11 semester 2.
Teknik Membaca dan Mencatat yang Efektif
Membaca materi PDF dengan cara yang tepat akan membantu kamu menyerap informasi dengan lebih baik. Hindari membaca sekilas dan langsung mengerjakan soal. Berikut adalah beberapa teknik yang bisa kamu terapkan:
- Baca dengan seksama: Bacalah setiap paragraf dengan cermat, pahami konsep dan rumus yang dijelaskan.
- Tandai bagian penting: Gunakan fitur penanda atau highlight untuk menandai bagian-bagian penting, rumus, dan definisi. Ini akan membantu kamu mengingat informasi penting dengan cepat saat kamu meninjau kembali.
- Buat catatan ringkas: Saat membaca, tuliskan catatan ringkas di margin atau di halaman terpisah. Catatan ini akan membantu kamu mengingat konsep dan rumus dengan lebih mudah.
- Gunakan diagram dan ilustrasi: Jika materi PDF berisi diagram atau ilustrasi, perhatikan dengan seksama. Ilustrasi visual dapat membantu kamu memahami konsep yang sulit dipahami dengan kata-kata.
Latihan Soal yang Terstruktur
Latihan soal merupakan bagian penting dalam belajar matematika. Materi PDF kelas 11 semester 2 biasanya dilengkapi dengan berbagai contoh soal dan latihan. Manfaatkan sumber ini dengan sebaik-baiknya. Berikut adalah beberapa tips untuk latihan soal yang efektif:
- Kerjakan contoh soal: Sebelum mengerjakan latihan soal, kerjakan terlebih dahulu contoh soal yang diberikan. Pahami langkah-langkah penyelesaiannya.
- Mulailah dari soal yang mudah: Jangan langsung mengerjakan soal yang sulit. Mulailah dari soal yang lebih mudah untuk membangun rasa percaya diri.
- Perhatikan kesalahan: Jika kamu membuat kesalahan, jangan langsung menyerah. Periksa kembali langkah-langkah penyelesaian dan pahami di mana letak kesalahannya.
- Mintalah bantuan jika perlu: Jika kamu kesulitan memahami suatu konsep atau menyelesaikan soal, jangan ragu untuk meminta bantuan guru atau teman.
Fitur Tambahan dalam PDF
Materi PDF memiliki beberapa fitur tambahan yang dapat membantu kamu belajar lebih efektif. Fitur-fitur ini dapat meningkatkan pemahaman dan retensi informasi. Berikut adalah beberapa fitur yang bisa kamu manfaatkan:
- Penanda dan Highlight: Gunakan fitur ini untuk menandai bagian-bagian penting, rumus, dan definisi. Ini akan membantu kamu mengingat informasi penting dengan cepat saat kamu meninjau kembali.
- Catatan: Gunakan fitur catatan untuk menambahkan catatan pribadi, pertanyaan, atau pemikiran kamu di margin atau di halaman terpisah. Ini akan membantu kamu mengingat informasi penting dan memahami konsep dengan lebih baik.
- Pencarian: Gunakan fitur pencarian untuk mencari kata kunci atau konsep tertentu dengan cepat.
- Zoom: Gunakan fitur zoom untuk memperbesar bagian tertentu dari materi PDF yang ingin kamu pelajari lebih detail.
Strategi Belajar dengan Materi PDF
Berikut adalah beberapa strategi belajar yang dapat kamu terapkan saat menggunakan materi PDF kelas 11 semester 2:
- Buat jadwal belajar yang terstruktur: Sediakan waktu khusus untuk belajar matematika setiap hari. Jadwal yang terstruktur akan membantu kamu fokus dan belajar secara konsisten.
- Buat kelompok belajar: Belajar bersama teman sekelas dapat membantu kamu memahami konsep yang sulit dan saling memotivasi.
- Manfaatkan sumber daya online: Ada banyak sumber daya online yang dapat membantu kamu belajar matematika, seperti video tutorial, latihan soal, dan forum diskusi.
- Berlatih secara rutin: Semakin sering kamu berlatih, semakin baik pemahaman kamu tentang konsep matematika.
Aplikasi dan Software Pendukung
Ada beberapa aplikasi dan software yang dapat membantu kamu belajar dengan materi PDF kelas 11 semester 2. Aplikasi ini dapat meningkatkan efektivitas belajar dan memudahkan akses ke materi.
- Adobe Acrobat Reader: Aplikasi ini adalah aplikasi pembaca PDF yang paling populer. Aplikasi ini memiliki berbagai fitur yang dapat membantu kamu belajar dengan materi PDF, seperti penanda, highlight, catatan, dan zoom.
- Xodo PDF Reader: Aplikasi ini memiliki fitur-fitur yang mirip dengan Adobe Acrobat Reader, tetapi aplikasi ini lebih ringan dan mudah digunakan.
- GoodNotes 5: Aplikasi ini dirancang khusus untuk mencatat dan membuat catatan digital. Aplikasi ini memungkinkan kamu untuk menulis, menggambar, dan menandai di atas PDF.
- Notability: Aplikasi ini mirip dengan GoodNotes 5, tetapi aplikasi ini memiliki lebih banyak fitur, seperti perekaman audio dan sinkronisasi catatan dengan perangkat lain.
Pemungkas
Dengan memanfaatkan materi matematika kelas 11 semester 2 PDF secara efektif, kamu dapat meningkatkan pemahaman dan hasil belajar. Materi ini menjadi teman belajar yang ideal, selalu siap membantu kamu dalam menghadapi tantangan matematika. Ingatlah, belajar matematika tidak harus selalu sulit. Dengan strategi belajar yang tepat dan sumber belajar yang memadai, seperti materi PDF ini, kamu dapat menaklukkan dunia matematika dengan percaya diri.