Perjalanan menapaki dunia perkuliahan, khususnya di bidang sains dan teknologi, pasti akan diiringi oleh matematika. Materi Matematika Kuliah Semester 1 merupakan fondasi yang kuat untuk membangun pemahaman lebih lanjut dalam berbagai bidang ilmu. Mulai dari aljabar yang mengasah kemampuan berpikir logis, hingga kalkulus yang membuka pintu menuju analisis dan pengukuran perubahan, semester ini akan menjadi petualangan intelektual yang menantang dan mengasyikkan.
Materi ini akan membahas berbagai topik penting seperti aljabar, kalkulus, dan geometri. Anda akan belajar bagaimana menyelesaikan persamaan, mengkaji fungsi, dan memahami konsep ruang dan bentuk. Tak hanya itu, Anda juga akan diajak untuk melihat bagaimana matematika diterapkan dalam berbagai bidang seperti ilmu komputer, ekonomi, dan fisika.
Materi Pokok Semester 1
Matematika merupakan dasar dari berbagai bidang ilmu pengetahuan dan teknologi. Di semester pertama perkuliahan, kamu akan diperkenalkan dengan konsep-konsep dasar matematika yang akan menjadi fondasi untuk mempelajari materi-materi lebih lanjut di semester berikutnya. Materi pokok matematika semester 1 umumnya mencakup aljabar, kalkulus, dan geometri.
Aljabar
Aljabar merupakan cabang matematika yang mempelajari operasi dan hubungan antara variabel, konstanta, dan fungsi. Topik-topik yang dipelajari dalam aljabar meliputi:
- Persamaan dan pertidaksamaan linear
- Sistem persamaan linear
- Fungsi linear dan kuadrat
- Matriks dan determinan
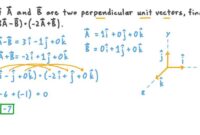
- Vektor dan ruang vektor
Aljabar memiliki aplikasi yang luas dalam berbagai bidang, seperti:
- Ilmu komputer: Aljabar digunakan dalam pengembangan algoritma dan pemrograman.
- Fisika: Aljabar digunakan untuk menyelesaikan persamaan gerak dan memahami konsep-konsep fisika.
- Ekonomi: Aljabar digunakan untuk memodelkan hubungan ekonomi dan memprediksi perilaku pasar.
Berikut contoh soal dan penyelesaian aljabar:
Selesaikan sistem persamaan linear berikut:
2x + 3y = 7
x – 2y = 1
Penyelesaian:
Untuk menyelesaikan sistem persamaan linear ini, kita dapat menggunakan metode eliminasi. Pertama, kita kalikan persamaan kedua dengan 2, sehingga kita mendapatkan:
2x + 3y = 7
2x – 4y = 2
Kemudian, kita kurangi kedua persamaan tersebut, sehingga kita mendapatkan:
7y = 5
Dengan demikian, y = 5/7. Selanjutnya, kita substitusikan nilai y ke dalam salah satu persamaan awal, misalnya persamaan kedua, sehingga kita mendapatkan:
x – 2(5/7) = 1
Dengan demikian, x = 19/7.
Jadi, solusi dari sistem persamaan linear tersebut adalah x = 19/7 dan y = 5/7.
Kalkulus, Materi matematika kuliah semester 1
Kalkulus merupakan cabang matematika yang mempelajari perubahan dan akumulasi. Topik-topik yang dipelajari dalam kalkulus meliputi:
- Limit dan kontinuitas
- Turunan dan aplikasi turunan
- Integral dan aplikasi integral
- Deret dan barisan
Kalkulus memiliki aplikasi yang luas dalam berbagai bidang, seperti:
- Fisika: Kalkulus digunakan untuk memahami konsep-konsep seperti kecepatan, percepatan, dan gaya.
- Teknik: Kalkulus digunakan dalam perancangan struktur, mesin, dan sistem.
- Ekonomi: Kalkulus digunakan untuk memodelkan pertumbuhan ekonomi dan perilaku pasar.
Berikut contoh soal dan penyelesaian kalkulus:
Tentukan turunan dari fungsi f(x) = x^2 + 2x + 1.
Penyelesaian:
Untuk menentukan turunan dari fungsi f(x), kita dapat menggunakan aturan turunan dasar. Aturan turunan dasar menyatakan bahwa turunan dari x^n adalah nx^(n-1). Dengan demikian, turunan dari f(x) adalah:
f'(x) = 2x + 2
Geometri
Geometri merupakan cabang matematika yang mempelajari bentuk, ukuran, dan posisi objek dalam ruang. Topik-topik yang dipelajari dalam geometri meliputi:
- Geometri bidang
- Geometri ruang
- Geometri analitik
- Geometri diferensial
Geometri memiliki aplikasi yang luas dalam berbagai bidang, seperti:
- Arsitektur: Geometri digunakan dalam perancangan bangunan dan struktur.
- Teknik: Geometri digunakan dalam perancangan mesin, alat, dan sistem.
- Seni: Geometri digunakan dalam seni rupa dan desain.
Berikut contoh soal dan penyelesaian geometri:
Tentukan luas segitiga dengan alas 10 cm dan tinggi 5 cm.
Penyelesaian:
Luas segitiga dapat dihitung dengan rumus:
Luas = (1/2) * alas * tinggi
Dengan demikian, luas segitiga tersebut adalah:
Luas = (1/2) * 10 cm * 5 cm = 25 cm^2
Jadi, luas segitiga tersebut adalah 25 cm^2.
Kaitan Materi dengan Program Studi
Matematika merupakan dasar ilmu pengetahuan yang memiliki peran penting dalam berbagai bidang studi. Materi matematika kuliah semester 1, yang meliputi kalkulus, aljabar linear, dan statistika, memiliki keterkaitan erat dengan berbagai program studi. Dalam pembahasan ini, kita akan mengkaji bagaimana materi tersebut diterapkan dalam program studi tertentu dan manfaatnya bagi pengembangan karir di masa depan.
Identifikasi Materi Matematika yang Relevan
Materi matematika kuliah semester 1 yang paling relevan dengan program studi ditentukan oleh bidang fokus studi tersebut. Sebagai contoh, program studi teknik akan lebih banyak menggunakan kalkulus dan aljabar linear, sedangkan program studi ekonomi akan lebih banyak menggunakan statistika dan aljabar linear.
Penerapan Materi Matematika dalam Bidang Studi
Penerapan materi matematika kuliah semester 1 dalam berbagai bidang studi dapat diilustrasikan dengan contoh kasus konkret. Sebagai contoh, dalam program studi teknik, kalkulus digunakan untuk menganalisis perilaku struktur bangunan, aljabar linear digunakan untuk menyelesaikan sistem persamaan dalam analisis jaringan listrik, dan statistika digunakan untuk mengolah data hasil pengujian material.
Simulasi Aplikasi Materi Matematika
Simulasi sederhana dapat menunjukkan aplikasi materi matematika kuliah semester 1 dalam program studi. Sebagai contoh, simulasi sederhana dapat dirancang untuk menghitung tegangan pada kabel listrik dengan menggunakan aljabar linear. Simulasi ini dapat menunjukkan bagaimana aljabar linear dapat digunakan untuk menyelesaikan masalah praktis dalam bidang teknik elektro.
Perbandingan Aplikasi Materi Matematika dalam Berbagai Program Studi
| Program Studi | Kalkulus | Aljabar Linear | Statistika |
|---|---|---|---|
| Teknik | Analisis struktur, dinamika fluida | Analisis jaringan, optimasi | Pengolahan data hasil pengujian |
| Ekonomi | Analisis pertumbuhan ekonomi, optimasi model ekonomi | Analisis pasar, portofolio investasi | Analisis data ekonomi, peramalan |
| Komputer | Algoritma, pemodelan sistem | Grafik komputer, machine learning | Analisis data, pengujian perangkat lunak |
Manfaat Penguasaan Materi Matematika untuk Karir
Penguasaan materi matematika kuliah semester 1 dapat membantu Anda dalam mencapai tujuan karir di masa depan. Dengan memahami konsep-konsep matematika, Anda akan memiliki kemampuan yang lebih baik dalam memecahkan masalah, menganalisis data, dan membuat keputusan yang tepat. Hal ini sangat penting dalam berbagai bidang pekerjaan, seperti teknik, ekonomi, komputer, dan penelitian.
Strategi Belajar Efektif: Materi Matematika Kuliah Semester 1
Matematika kuliah semester 1 seringkali menjadi tantangan bagi banyak mahasiswa. Materi yang abstrak dan kompleks, serta metode penyelesaian yang baru, memerlukan strategi belajar yang efektif. Artikel ini akan membahas beberapa strategi belajar yang dapat membantu Anda memahami materi matematika kuliah semester 1 dengan lebih mudah.
Langkah-langkah Belajar Bertahap
Mempelajari matematika secara bertahap akan membantu Anda memahami konsep dengan lebih baik. Berikut adalah langkah-langkah yang dapat Anda ikuti:
- Pahami konsep dasar: Pastikan Anda memahami konsep dasar sebelum mempelajari materi yang lebih kompleks. Jika ada konsep yang belum dipahami, jangan ragu untuk bertanya kepada dosen atau teman sekelas.
- Latih soal-soal: Setelah memahami konsep, latih soal-soal untuk menguji pemahaman Anda. Mulailah dengan soal-soal yang mudah, kemudian tingkatkan kesulitannya secara bertahap.
- Buat catatan: Catat poin-poin penting dan rumus-rumus yang Anda pelajari. Gunakan metode catatan yang paling efektif bagi Anda, seperti mind mapping, diagram, atau catatan konvensional.
- Berdiskusi dengan teman: Berdiskusi dengan teman sekelas tentang materi yang sulit dipahami. Bertukar ide dan cara pandang dapat membantu Anda memahami konsep dengan lebih baik.
- Tinjau kembali materi: Tinjau kembali materi yang sudah dipelajari secara berkala. Hal ini akan membantu Anda mengingat konsep dan rumus dengan lebih baik.
Sumber Belajar Tambahan
Selain buku teks, Anda dapat memanfaatkan sumber belajar tambahan untuk memperkaya pemahaman Anda. Beberapa sumber belajar tambahan yang dapat Anda manfaatkan:
- Buku referensi: Cari buku referensi lain yang membahas materi yang sama dengan buku teks Anda.
- Website: Banyak website yang menyediakan materi matematika kuliah semester 1, seperti Khan Academy, Coursera, dan EdX.
- Video tutorial: Youtube dan platform video online lainnya menyediakan banyak video tutorial tentang materi matematika kuliah semester 1.
Rencana Belajar Terstruktur
Membuat rencana belajar yang terstruktur akan membantu Anda belajar dengan lebih efektif. Berikut adalah contoh rencana belajar yang dapat Anda gunakan:
- Tentukan target belajar: Tentukan target yang ingin dicapai dalam jangka waktu tertentu, misalnya memahami konsep dasar aljabar dalam satu minggu.
- Buat jadwal belajar: Buat jadwal belajar yang realistis dan dapat Anda ikuti. Pastikan jadwal belajar Anda mencakup waktu untuk membaca materi, latihan soal, dan berdiskusi dengan teman.
- Evaluasi hasil belajar: Evaluasi hasil belajar Anda secara berkala. Gunakan tes atau kuis untuk mengukur pemahaman Anda terhadap materi yang sudah dipelajari.
Tips Mengatasi Kesulitan
Tidak semua orang mudah memahami matematika. Berikut adalah beberapa tips untuk mengatasi kesulitan dalam memahami materi matematika kuliah semester 1:
- Jangan takut bertanya: Jika ada materi yang tidak dipahami, jangan ragu untuk bertanya kepada dosen, asisten dosen, atau teman sekelas.
- Cari tutor: Jika Anda merasa kesulitan memahami materi, cari tutor yang dapat membantu Anda.
- Latih soal-soal: Semakin banyak soal yang Anda latih, semakin baik pemahaman Anda terhadap konsep matematika.
- Gunakan metode belajar yang efektif: Temukan metode belajar yang paling efektif bagi Anda. Ada banyak metode belajar yang dapat Anda coba, seperti metode Feynman, metode PQ4R, atau metode Cornell Notes.
- Bersikap positif: Sikap positif sangat penting dalam belajar matematika. Jangan mudah menyerah dan tetaplah bersemangat dalam mempelajari materi.
Pentingnya Pemahaman Konsep
Matematika kuliah semester 1 merupakan fondasi bagi pemahaman konsep matematika tingkat lanjut. Memahami konsep dengan baik akan membuka jalan bagi Anda untuk menguasai materi yang lebih kompleks di semester-semester berikutnya. Tidak hanya itu, pemahaman konsep yang kuat akan membantu Anda dalam memecahkan masalah yang lebih menantang dan mengembangkan kemampuan berpikir kritis Anda.
Mengapa Pemahaman Konsep Sangat Penting?
Matematika kuliah semester 1 umumnya membahas konsep dasar seperti aljabar, kalkulus, dan trigonometri. Konsep-konsep ini saling terkait dan merupakan dasar untuk mempelajari topik-topik matematika yang lebih kompleks di masa depan. Jika Anda hanya menghafal rumus tanpa memahami konsep di baliknya, Anda akan kesulitan dalam menyelesaikan soal-soal yang lebih menantang. Pemahaman konsep memungkinkan Anda untuk menerapkan rumus dengan tepat dalam berbagai situasi dan memecahkan masalah dengan lebih mudah.
Contoh Penerapan Pemahaman Konsep
Misalnya, dalam kalkulus, konsep turunan digunakan untuk menentukan laju perubahan suatu fungsi. Jika Anda hanya menghafal rumus turunan, Anda mungkin kesulitan memahami bagaimana turunan diterapkan dalam berbagai situasi, seperti menentukan kecepatan dan percepatan suatu benda. Namun, jika Anda memahami konsep turunan, Anda dapat dengan mudah menerapkannya dalam berbagai situasi dan memecahkan masalah yang lebih kompleks.
Manfaat Pemahaman Konsep vs Hafalan
| Aspek | Pemahaman Konsep | Hafalan |
|---|---|---|
| Kemampuan Pemecahan Masalah | Meningkatkan kemampuan memecahkan masalah yang kompleks dan tidak terstruktur. | Membatasi kemampuan pemecahan masalah hanya pada soal-soal yang mirip dengan contoh yang dihafal. |
| Penerapan Konsep | Memungkinkan penerapan konsep dalam berbagai situasi dan konteks. | Membuat penerapan konsep menjadi terbatas pada situasi yang sama dengan contoh yang dihafal. |
| Kemampuan Berpikir Kritis | Meningkatkan kemampuan berpikir kritis dan analitis. | Membatasi kemampuan berpikir kritis dan analitis. |
| Motivasi Belajar | Meningkatkan motivasi belajar karena memahami konsep membuat belajar matematika lebih menarik dan bermanfaat. | Membuat belajar matematika menjadi membosankan dan kurang bermanfaat karena hanya fokus pada menghafal rumus. |
Kegiatan untuk Memperdalam Pemahaman Konsep
- Belajar aktif: Jangan hanya membaca buku teks, tetapi aktiflah dalam memahami konsep dengan membuat catatan, mengerjakan latihan soal, dan mendiskusikan konsep dengan teman.
- Mencari contoh: Carilah contoh penerapan konsep dalam kehidupan nyata atau dalam bidang lain yang Anda minati. Hal ini akan membantu Anda memahami konsep dengan lebih baik dan melihat manfaatnya dalam kehidupan sehari-hari.
- Berlatih dengan soal-soal yang menantang: Jangan takut untuk mengerjakan soal-soal yang lebih menantang. Soal-soal yang sulit akan memaksa Anda untuk berpikir lebih dalam dan memahami konsep dengan lebih baik.
- Berdiskusi dengan dosen atau tutor: Jangan ragu untuk bertanya kepada dosen atau tutor jika Anda mengalami kesulitan memahami konsep. Mereka dapat memberikan penjelasan yang lebih mudah dipahami dan membantu Anda dalam mengatasi kesulitan yang Anda alami.
Dampak Positif Pemahaman Konsep
Pemahaman konsep dalam matematika kuliah semester 1 memiliki dampak positif terhadap perkembangan intelektual dan kemampuan memecahkan masalah. Dengan memahami konsep, Anda akan dapat berpikir lebih kritis, analitis, dan logis. Hal ini akan membantu Anda dalam menghadapi berbagai tantangan di kehidupan, baik dalam bidang akademis maupun profesional.
Penutup
Dengan memahami konsep dasar matematika di semester 1, Anda akan memiliki bekal yang kuat untuk menghadapi tantangan di semester-semester berikutnya. Mempelajari matematika tidak hanya tentang menghafal rumus, tetapi juga tentang memahami konsep dan bagaimana konsep tersebut diterapkan dalam berbagai situasi. Jadi, bersiaplah untuk menjelajahi dunia matematika yang penuh keajaiban dan membuka potensi diri Anda untuk berpikir lebih kritis dan kreatif.