Pangkat matematika dalam bahasa Inggris, atau “mathematical powers,” adalah konsep fundamental dalam matematika yang memungkinkan kita untuk mengekspresikan perkalian berulang dengan cara yang lebih ringkas. Bayangkan Anda ingin menuliskan perkalian 5 x 5 x 5 x 5 x 5. Alih-alih menuliskannya secara berulang, Anda dapat menggunakan pangkat dan menuliskannya sebagai 5 pangkat 5 atau 5⁵.
Konsep pangkat matematika memiliki banyak aplikasi dalam berbagai bidang, mulai dari ilmu pengetahuan dan teknologi hingga keuangan dan ekonomi. Dalam artikel ini, kita akan menjelajahi dunia pangkat matematika, mulai dari pengertian dasar hingga aplikasi praktisnya dalam kehidupan sehari-hari.
Solving Problems with Mathematical Powers: Pangkat Matematika Dalam Bahasa Inggris
![]()
Solving problems involving mathematical powers requires a deep understanding of the concepts and the ability to apply them effectively. There are several techniques that can be employed to tackle these problems, and each technique offers a unique approach to finding the solution.
Understanding the Concepts
Before diving into the techniques, it’s crucial to have a firm grasp of the fundamental concepts of mathematical powers. Powers, or exponents, represent repeated multiplication of a base number by itself a certain number of times. For instance, 23 indicates multiplying 2 by itself three times (2 × 2 × 2 = 8). Understanding the properties of powers, such as the product rule, quotient rule, and power of a power rule, is essential for simplifying expressions and solving equations involving powers.
Common Techniques for Solving Problems, Pangkat matematika dalam bahasa inggris
Various techniques can be applied to solve problems involving mathematical powers. These techniques can be categorized based on the type of problem and the approach employed. Here’s a breakdown of some common techniques:
- Simplification: This technique involves rewriting expressions involving powers in a simpler form. This can be achieved by using the properties of powers to combine terms, expand expressions, or reduce fractions. For example, simplifying the expression 23 × 22 using the product rule (xm × xn = xm+n) results in 25, which can be further simplified to 32.
- Substitution: This technique involves replacing a variable or expression with another equivalent value to simplify the problem. For instance, if we have the equation 2x = 8, we can substitute 8 with 23, making the equation 2x = 23. From this, we can easily deduce that x = 3.
- Factoring: Factoring involves expressing a polynomial as a product of simpler expressions. This technique can be used to solve equations involving powers by isolating the variable and finding its value. For example, the equation x2 – 4 = 0 can be factored into (x + 2)(x – 2) = 0, leading to the solutions x = -2 and x = 2.
- Using Logarithms: Logarithms are the inverse operation of exponentiation. They can be used to solve equations where the variable is in the exponent. For instance, to solve the equation 2x = 5, we can take the logarithm of both sides to obtain x log(2) = log(5), and then solve for x: x = log(5) / log(2).
- Graphical Methods: Visualizing the behavior of functions involving powers can help in solving problems. By plotting the graphs of the functions, we can identify the points of intersection, which represent the solutions to the equations. For example, plotting the graphs of y = x2 and y = 2x + 1 can reveal the points where the two functions intersect, representing the solutions to the equation x2 = 2x + 1.
Example Problem
Let’s consider the problem of finding the value of x in the equation 3x = 27. We can solve this problem using the substitution technique. Since 27 is equal to 33, we can rewrite the equation as 3x = 33. By comparing the exponents, we can conclude that x = 3.
Table of Techniques
| Technique | Description | Example |
|---|---|---|
| Simplification | Rewriting expressions involving powers in a simpler form. | 23 × 22 = 25 = 32 |
| Substitution | Replacing a variable or expression with another equivalent value. | 2x = 8 → 2x = 23 → x = 3 |
| Factoring | Expressing a polynomial as a product of simpler expressions. | x2 – 4 = 0 → (x + 2)(x – 2) = 0 → x = -2 or x = 2 |
| Logarithms | Using the inverse operation of exponentiation to solve equations. | 2x = 5 → x log(2) = log(5) → x = log(5) / log(2) |
| Graphical Methods | Visualizing functions involving powers to identify solutions. | Plotting y = x2 and y = 2x + 1 to find the points of intersection. |
Terakhir
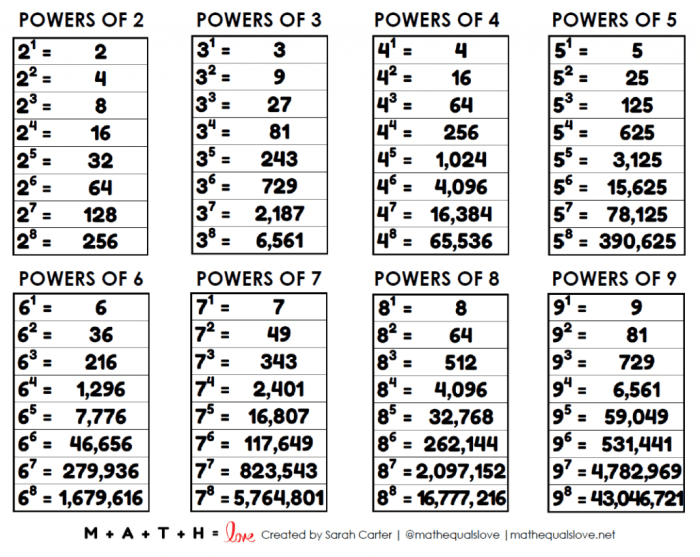
Memahami pangkat matematika dalam bahasa Inggris, atau “mathematical powers,” adalah kunci untuk menguasai konsep matematika yang lebih kompleks. Dengan pemahaman yang kuat tentang konsep ini, Anda akan mampu menyelesaikan berbagai masalah matematika dengan lebih mudah dan efisien. Selain itu, pengetahuan tentang pangkat matematika akan membantu Anda dalam memahami berbagai fenomena di sekitar kita, mulai dari pertumbuhan populasi hingga perhitungan bunga di bank.