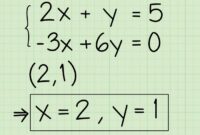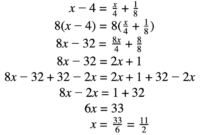Pengertian matematika – Matematika, bahasa universal yang menaklukkan dunia, adalah ilmu yang mempelajari pola, struktur, dan hubungan. Dari menghitung apel di pasar hingga merancang roket antariksa, matematika hadir dalam setiap aspek kehidupan kita.
Matematika bukanlah sekadar deretan angka dan rumus yang rumit. Ia adalah alat berpikir yang ampuh, membantu kita memahami dunia di sekitar kita dengan lebih baik. Dengan matematika, kita dapat mengukur, menganalisis, dan memprediksi berbagai fenomena, baik yang sederhana maupun yang kompleks.
Pengertian Matematika
Matematika adalah ilmu yang mempelajari tentang pola, struktur, dan hubungan. Ilmu ini menggunakan logika dan penalaran deduktif untuk mempelajari konsep-konsep seperti jumlah, bentuk, dan ruang. Matematika adalah bahasa universal yang digunakan untuk memahami dan menjelaskan dunia di sekitar kita.
Peran Matematika dalam Kehidupan Sehari-hari
Matematika berperan penting dalam kehidupan sehari-hari kita. Tanpa matematika, kita tidak akan dapat melakukan banyak hal yang kita lakukan setiap hari, seperti:
- Membeli barang di toko dan menghitung uang kembalian
- Memasak makanan dengan mengikuti resep
- Mengukur bahan bangunan untuk membangun rumah
- Menghitung waktu untuk pergi ke suatu tempat
- Memahami grafik dan statistik untuk membuat keputusan yang tepat
Penerapan Matematika dalam Berbagai Bidang
Matematika diterapkan dalam berbagai bidang, seperti:
Sains
Matematika merupakan alat penting dalam sains. Para ilmuwan menggunakan matematika untuk:
- Membuat model dan simulasi untuk memahami fenomena alam
- Menganalisis data eksperimen dan penelitian
- Mengembangkan teori dan hukum ilmiah
Teknologi
Matematika berperan penting dalam pengembangan teknologi. Matematika digunakan untuk:
- Membangun komputer dan perangkat lunak
- Mengembangkan algoritma untuk mengolah data
- Merancang dan membangun infrastruktur seperti jembatan dan gedung
Ekonomi
Matematika digunakan dalam ekonomi untuk:
- Menganalisis data ekonomi dan membuat prediksi
- Mengembangkan model ekonomi untuk memahami perilaku pasar
- Mengatur keuangan dan investasi
Seni
Matematika juga diterapkan dalam seni. Contohnya:
- Proporsi dan simetri dalam lukisan dan arsitektur
- Pola dan urutan dalam musik
- Geometri dalam desain grafis
Cabang Matematika dan Penerapannya, Pengertian matematika
Matematika memiliki banyak cabang, masing-masing dengan fokus dan aplikasi yang berbeda. Berikut adalah beberapa contoh cabang matematika dan penerapannya dalam kehidupan sehari-hari:
| Cabang Matematika | Penerapan dalam Kehidupan Sehari-hari |
|---|---|
| Aritmetika | Menghitung uang, menghitung waktu, membuat resep |
| Aljabar | Memecahkan persamaan, menganalisis data, membuat model ekonomi |
| Geometri | Membangun rumah, mendesain furnitur, membuat peta |
| Statistika | Menganalisis data, membuat prediksi, mengukur risiko |
| Kalkulus | Menganalisis perubahan dan gerakan, membuat model ilmiah |
Sejarah Matematika
Matematika, sebagai bahasa universal yang mendasari berbagai aspek kehidupan, memiliki sejarah panjang dan kaya yang menjangkau berbagai peradaban dan budaya. Perkembangannya tidak terjadi secara tiba-tiba, melainkan melalui proses evolusi yang berkelanjutan, dibentuk oleh pemikiran para ilmuwan, penemu, dan ahli matematika dari berbagai zaman.
Zaman Kuno
Peradaban awal seperti Mesir Kuno dan Babilonia telah menunjukkan pemahaman matematika yang signifikan. Mereka mengembangkan sistem bilangan, geometri dasar, dan aljabar sederhana untuk keperluan praktis seperti pertanian, arsitektur, dan astronomi.
- Mesir Kuno: Sistem bilangan desimal, geometri, dan penggunaan persamaan linear dalam bidang arsitektur dan pembangunan piramida.
- Babilonia: Sistem bilangan berbasis 60, aljabar, dan penggunaan persamaan kuadrat dalam astronomi dan kalender.
Zaman Yunani Kuno
Zaman Yunani Kuno menandai era penting dalam perkembangan matematika. Filsuf dan matematikawan Yunani seperti Pythagoras, Euclid, dan Archimedes memberikan kontribusi besar dalam berbagai bidang matematika, termasuk geometri, teori bilangan, dan kalkulus.
- Pythagoras: Teorema Pythagoras, yang menghubungkan sisi-sisi segitiga siku-siku.
- Euclid: Geometri Euclid, yang mendirikan dasar-dasar geometri klasik.
- Archimedes: Kalkulus integral, metode untuk menghitung luas dan volume benda-benda geometri.
Zaman Pertengahan
Selama Zaman Pertengahan, matematika berkembang pesat di dunia Islam. Ilmuwan dan matematikawan Muslim seperti Al-Khwarizmi, Al-Battani, dan Ibn Sina memberikan kontribusi penting dalam bidang aljabar, trigonometri, dan astronomi.
- Al-Khwarizmi: Penemu aljabar, yang mengembangkan metode sistematis untuk menyelesaikan persamaan.
- Al-Battani: Penemu trigonometri, yang mengembangkan tabel trigonometri dan menggunakannya dalam astronomi.
- Ibn Sina: Ilmuwan dan filsuf yang menulis tentang logika, filsafat, dan matematika.
Zaman Modern
Zaman Modern menandai periode kemajuan besar dalam matematika. Tokoh-tokoh seperti Newton, Leibniz, Euler, dan Gauss memberikan kontribusi yang mendalam dalam bidang kalkulus, teori bilangan, dan geometri analitik.
- Newton: Kalkulus diferensial dan integral, hukum gravitasi universal.
- Leibniz: Kalkulus diferensial dan integral, notasi matematika modern.
- Euler: Teori bilangan, kalkulus, dan topologi.
- Gauss: Teori bilangan, geometri, dan statistik.
Pengaruh Budaya dan Peradaban
Perkembangan matematika dipengaruhi oleh budaya dan peradaban di berbagai belahan dunia. Misalnya, matematika Cina kuno mengembangkan sistem bilangan, aljabar, dan geometri, sementara matematika India kuno mengembangkan konsep nol dan sistem desimal.
| Peradaban | Kontribusi |
|---|---|
| Mesir Kuno | Sistem bilangan desimal, geometri, dan penggunaan persamaan linear dalam bidang arsitektur dan pembangunan piramida. |
| Babilonia | Sistem bilangan berbasis 60, aljabar, dan penggunaan persamaan kuadrat dalam astronomi dan kalender. |
| Yunani Kuno | Geometri Euclid, teori bilangan, dan kalkulus. |
| Peradaban Islam | Aljabar, trigonometri, dan astronomi. |
| Cina Kuno | Sistem bilangan, aljabar, dan geometri. |
| India Kuno | Konsep nol dan sistem desimal. |
Garis Waktu Perkembangan Matematika
Berikut adalah garis waktu yang menunjukkan perkembangan penting dalam sejarah matematika:
- 3000 SM: Peradaban Mesir Kuno dan Babilonia mengembangkan sistem bilangan, geometri, dan aljabar dasar.
- 600 SM: Pythagoras mengemukakan teorema Pythagoras.
- 300 SM: Euclid menulis “Elements”, yang menjadi dasar geometri klasik.
- 250 SM: Archimedes mengembangkan kalkulus integral.
- 820 M: Al-Khwarizmi mengemukakan konsep aljabar.
- 850 M: Al-Battani mengembangkan tabel trigonometri.
- 1000 M: Ibn Sina menulis tentang logika, filsafat, dan matematika.
- 1665-1666: Isaac Newton mengembangkan kalkulus diferensial dan integral.
- 1675: Gottfried Wilhelm Leibniz mengembangkan kalkulus diferensial dan integral.
- 1700-an: Leonhard Euler membuat kontribusi besar dalam teori bilangan, kalkulus, dan topologi.
- 1800-an: Carl Friedrich Gauss membuat kontribusi besar dalam teori bilangan, geometri, dan statistik.
Prinsip-Prinsip Dasar Matematika

Matematika merupakan ilmu yang mempelajari tentang pola, struktur, dan hubungan. Ilmu ini dibangun atas dasar prinsip-prinsip dasar yang membentuk fondasi bagi berbagai konsep dan teori matematika yang lebih kompleks. Prinsip-prinsip dasar ini merupakan batu bata yang membentuk bangunan matematika yang kita kenal sekarang.
Bilangan
Bilangan merupakan konsep dasar dalam matematika yang mewakili kuantitas atau jumlah. Bilangan dapat berupa bilangan bulat, pecahan, desimal, dan bilangan real.
- Bilangan bulat adalah bilangan yang tidak memiliki bagian pecahan, seperti 1, 2, 3, -1, -2, -3, dan seterusnya.
- Pecahan adalah bilangan yang mewakili bagian dari keseluruhan, seperti 1/2, 2/3, 3/4, dan seterusnya.
- Bilangan desimal adalah bilangan yang menggunakan tanda koma untuk memisahkan bagian bulat dan bagian pecahan, seperti 1.5, 2.75, 3.14, dan seterusnya.
- Bilangan real adalah gabungan dari bilangan bulat, pecahan, dan desimal, termasuk bilangan irasional seperti π (pi) dan √2.
Operasi Matematika
Operasi matematika adalah aturan yang digunakan untuk menggabungkan atau memanipulasi bilangan. Operasi dasar dalam matematika meliputi penjumlahan, pengurangan, perkalian, dan pembagian.
- Penjumlahan adalah operasi yang menggabungkan dua bilangan untuk mendapatkan jumlahnya. Contoh: 2 + 3 = 5.
- Pengurangan adalah operasi yang mengurangi satu bilangan dari bilangan lainnya untuk mendapatkan selisihnya. Contoh: 5 – 2 = 3.
- Perkalian adalah operasi yang mengulang penjumlahan bilangan yang sama sebanyak tertentu. Contoh: 2 x 3 = 2 + 2 + 2 = 6.
- Pembagian adalah operasi yang membagi satu bilangan dengan bilangan lainnya untuk mendapatkan hasil bagi. Contoh: 6 / 2 = 3.
Aljabar
Aljabar adalah cabang matematika yang mempelajari tentang variabel, persamaan, dan fungsi. Dalam aljabar, variabel digunakan untuk mewakili bilangan yang tidak diketahui, dan persamaan digunakan untuk menyatakan hubungan antara variabel.
- Variabel adalah simbol yang mewakili bilangan yang tidak diketahui. Contoh: x, y, z.
- Persamaan adalah pernyataan yang menyatakan bahwa dua ekspresi aljabar sama. Contoh: x + 2 = 5.
- Fungsi adalah aturan yang menghubungkan setiap nilai input dengan satu nilai output. Contoh: f(x) = x + 2.
Geometri
Geometri adalah cabang matematika yang mempelajari tentang bentuk, ukuran, dan posisi objek dalam ruang. Geometri mempelajari berbagai konsep seperti titik, garis, bidang, sudut, bangun datar, dan bangun ruang.
- Titik adalah lokasi tunggal dalam ruang. Titik tidak memiliki dimensi.
- Garis adalah kumpulan titik yang terhubung secara terus menerus dalam satu arah. Garis memiliki satu dimensi, yaitu panjang.
- Bidang adalah permukaan datar yang tidak terbatas. Bidang memiliki dua dimensi, yaitu panjang dan lebar.
- Sudut adalah ruang antara dua garis yang bertemu pada titik yang sama. Sudut diukur dalam derajat.
- Bangun datar adalah objek dua dimensi yang memiliki batas berupa garis lurus atau lengkung. Contoh: segitiga, persegi, lingkaran.
- Bangun ruang adalah objek tiga dimensi yang memiliki batas berupa permukaan. Contoh: kubus, bola, kerucut.
Kalkulus
Kalkulus adalah cabang matematika yang mempelajari tentang perubahan. Kalkulus mempelajari konsep-konsep seperti turunan, integral, dan limit. Kalkulus digunakan untuk memecahkan masalah yang melibatkan perubahan kontinu, seperti kecepatan, percepatan, dan volume.
- Turunan adalah laju perubahan suatu fungsi terhadap perubahan variabel input. Turunan digunakan untuk menentukan kemiringan garis singgung pada kurva.
- Integral adalah operasi kebalikan dari turunan. Integral digunakan untuk menghitung luas daerah di bawah kurva.
- Limit adalah nilai yang didekati oleh suatu fungsi saat variabel input mendekati nilai tertentu. Limit digunakan untuk mendefinisikan konsep kontinuitas dan turunan.
Hubungan Antar Konsep Dasar Matematika
Konsep-konsep dasar matematika saling berhubungan dan membentuk sistem matematika yang koheren. Misalnya, bilangan digunakan dalam aljabar untuk mewakili variabel dan menyelesaikan persamaan. Geometri menggunakan konsep bilangan untuk menentukan ukuran dan bentuk objek. Kalkulus menggunakan konsep bilangan, aljabar, dan geometri untuk mempelajari perubahan dan menentukan luas dan volume.
Diagram di atas menunjukkan hubungan antar konsep dasar matematika. Setiap konsep merupakan bagian integral dari sistem matematika yang saling terkait.
Peran Matematika dalam Berbagai Bidang
/common-mathematic-symbols-2312232_final_CORRECTED-d1b3858039ce4668b3ae0b028da7a258.png?w=700)
Matematika bukan hanya sekumpulan rumus dan angka, tetapi juga alat yang kuat untuk memahami dunia di sekitar kita. Matematika berperan penting dalam berbagai bidang, dari sains dan teknologi hingga ekonomi dan seni.
Matematika dalam Sains
Matematika merupakan bahasa universal dalam sains. Dalam bidang fisika, matematika digunakan untuk merumuskan hukum-hukum alam, seperti hukum gravitasi dan hukum gerak Newton. Dalam kimia, matematika digunakan untuk memahami reaksi kimia, menentukan komposisi zat, dan menghitung energi yang terlibat dalam reaksi. Dalam biologi, matematika digunakan untuk memodelkan populasi, menganalisis data genetika, dan memahami proses evolusi. Dalam astronomi, matematika digunakan untuk menghitung jarak bintang dan galaksi, memprediksi pergerakan planet, dan memahami struktur alam semesta.
Matematika dalam Teknologi
Perkembangan teknologi modern tidak lepas dari peran matematika. Dalam bidang komputer, matematika digunakan untuk mengembangkan algoritma, membangun sistem operasi, dan menciptakan perangkat lunak. Dalam robotika, matematika digunakan untuk mengontrol gerakan robot, menavigasi lingkungan, dan mengoptimalkan kinerja robot. Dalam telekomunikasi, matematika digunakan untuk mengembangkan sistem komunikasi, mengoptimalkan jaringan, dan mengamankan data.
Matematika dalam Ekonomi
Matematika memainkan peran penting dalam memahami dan mengelola ekonomi. Dalam bidang keuangan, matematika digunakan untuk menghitung bunga, mengelola investasi, dan menganalisis risiko. Dalam manajemen, matematika digunakan untuk mengoptimalkan proses produksi, merencanakan strategi bisnis, dan membuat keputusan berdasarkan data. Dalam pemasaran, matematika digunakan untuk menganalisis data konsumen, mengoptimalkan kampanye pemasaran, dan mengukur efektivitas strategi pemasaran.
Matematika dalam Seni
Matematika mungkin tampak tidak berhubungan dengan seni, tetapi sebenarnya ada hubungan yang erat antara keduanya. Dalam musik, matematika digunakan untuk menentukan nada, ritme, dan harmoni. Dalam arsitektur, matematika digunakan untuk mendesain bangunan yang kokoh dan estetis. Dalam desain, matematika digunakan untuk menciptakan pola, bentuk, dan komposisi yang menarik.
Manfaat Mempelajari Matematika

Matematika adalah ilmu yang mempelajari tentang pola, struktur, dan hubungan. Matematika tidak hanya sekedar tentang angka dan rumus, tetapi juga tentang cara berpikir logis dan sistematis. Mempelajari matematika memiliki banyak manfaat, baik untuk kehidupan sehari-hari maupun untuk masa depan.
Meningkatkan Kemampuan Berpikir Logis dan Analitis
Matematika mengajarkan kita untuk berpikir logis dan analitis. Kita dilatih untuk memecahkan masalah dengan langkah-langkah yang sistematis, mengidentifikasi pola, dan menarik kesimpulan berdasarkan data yang ada. Kemampuan ini sangat berguna dalam berbagai aspek kehidupan, seperti dalam pengambilan keputusan, menyelesaikan masalah, dan memahami informasi yang kompleks.
Meningkatkan Kemampuan Memecahkan Masalah
Matematika membantu kita mengembangkan kemampuan memecahkan masalah. Melalui berbagai latihan soal dan pembahasan, kita belajar untuk mengidentifikasi masalah, merumuskan strategi, dan menemukan solusi yang tepat. Kemampuan ini sangat penting dalam menghadapi berbagai tantangan yang kita hadapi dalam kehidupan sehari-hari, baik di bidang pekerjaan, pendidikan, maupun dalam kehidupan pribadi.
Meningkatkan Kemampuan Berkomunikasi dan Berkolaborasi
Matematika juga mengajarkan kita untuk berkomunikasi dan berkolaborasi secara efektif. Dalam proses belajar matematika, kita seringkali berdiskusi dengan teman, guru, atau mentor untuk memahami konsep dan menyelesaikan masalah. Hal ini membantu kita untuk mengembangkan kemampuan menyampaikan ide, mendengarkan pendapat orang lain, dan bekerja sama untuk mencapai tujuan bersama.
Membuka Peluang Karir di Berbagai Bidang
Mempelajari matematika membuka peluang karir di berbagai bidang, seperti:
- Ilmu Komputer: Matematika merupakan dasar dari ilmu komputer, khususnya dalam bidang pemrograman, algoritma, dan analisis data.
- Teknik: Matematika digunakan secara luas dalam bidang teknik, seperti teknik sipil, teknik mesin, dan teknik elektro, untuk merancang dan membangun berbagai infrastruktur dan peralatan.
- Ekonomi dan Keuangan: Matematika sangat penting dalam bidang ekonomi dan keuangan, seperti dalam analisis pasar, pengelolaan portofolio, dan pemodelan keuangan.
- Statistika dan Analisis Data: Matematika digunakan untuk mengumpulkan, menganalisis, dan menginterpretasikan data, yang sangat berguna dalam berbagai bidang, seperti penelitian, bisnis, dan kesehatan.
- Pendidikan: Guru matematika berperan penting dalam mendidik generasi muda untuk memiliki kemampuan berpikir logis dan analitis.
Akhir Kata
Mempelajari matematika bukan hanya tentang menghafal rumus, tetapi juga tentang mengembangkan kemampuan berpikir logis, analitis, dan kritis. Matematika adalah kunci untuk membuka pintu menuju berbagai peluang dan tantangan di masa depan, mempersiapkan kita untuk menghadapi dunia yang semakin kompleks dan penuh dengan misteri.