Pengertian sistem bilangan dalam ilmu komputer – Pernahkah Anda bertanya-tanya bagaimana komputer memahami bahasa kita? Bagaimana komputer memproses informasi yang kita masukkan dan menampilkan hasil yang kita inginkan? Jawabannya terletak pada sistem bilangan, konsep fundamental dalam ilmu komputer yang menjadi dasar bagi segala aktivitas komputer. Sistem bilangan adalah bahasa yang digunakan komputer untuk berkomunikasi dan memproses data, layaknya alfabet yang kita gunakan untuk menulis dan berbicara.
Sistem bilangan dalam ilmu komputer, khususnya sistem bilangan biner, merupakan fondasi yang memungkinkan komputer untuk menjalankan tugasnya. Sistem bilangan biner, yang hanya menggunakan angka 0 dan 1, memungkinkan komputer untuk memproses informasi dengan cepat dan efisien. Dalam artikel ini, kita akan menjelajahi dunia sistem bilangan, mempelajari berbagai jenisnya, cara kerjanya, dan bagaimana sistem bilangan ini membentuk cara komputer berpikir dan berinteraksi dengan dunia.
Pengertian Sistem Bilangan
Sistem bilangan adalah cara untuk merepresentasikan angka menggunakan simbol-simbol tertentu. Dalam kehidupan sehari-hari, kita menggunakan sistem bilangan desimal (basis 10) yang menggunakan sepuluh digit (0-9). Namun, dalam ilmu komputer, kita menggunakan sistem bilangan biner (basis 2), oktal (basis 8), dan heksadesimal (basis 16) untuk mewakili data dan instruksi komputer.
Tujuan Penggunaan Sistem Bilangan dalam Ilmu Komputer
Sistem bilangan memegang peranan penting dalam ilmu komputer karena memungkinkan komputer untuk memahami dan memproses data dengan efisien. Berikut adalah beberapa tujuan utama penggunaan sistem bilangan dalam ilmu komputer:
- Representasi Data: Sistem bilangan digunakan untuk merepresentasikan berbagai jenis data, seperti angka, karakter, dan instruksi, dalam bentuk yang dapat dipahami oleh komputer.
- Pemrosesan Data: Komputer menggunakan sistem bilangan untuk melakukan operasi aritmatika dan logika pada data, seperti penjumlahan, pengurangan, perkalian, dan pembagian.
- Penyimpanan Data: Data disimpan dalam bentuk digital menggunakan sistem bilangan biner, di mana setiap bit (0 atau 1) mewakili satu unit data.
- Komunikasi Data: Sistem bilangan digunakan untuk mentransmisikan data antara komputer dan perangkat lain, seperti printer, monitor, dan jaringan.
Contoh Penggunaan Sistem Bilangan dalam Kehidupan Sehari-hari, Pengertian sistem bilangan dalam ilmu komputer
Meskipun kita mungkin tidak menyadarinya, sistem bilangan digunakan dalam berbagai aspek kehidupan sehari-hari. Berikut beberapa contohnya:
- Jam Digital: Jam digital menggunakan sistem bilangan desimal untuk menampilkan waktu. Misalnya, 10:30 berarti 10 jam dan 30 menit.
- Kode Bar: Kode bar pada produk menggunakan kombinasi garis tebal dan tipis untuk mewakili angka dan karakter, yang diinterpretasikan oleh pemindai menggunakan sistem bilangan.
- Kartu Kredit: Nomor kartu kredit terdiri dari serangkaian angka yang mewakili informasi tentang pemilik kartu dan bank penerbit. Sistem bilangan digunakan untuk mengenkripsi dan mengamankan data ini.
Konversi Antar Sistem Bilangan
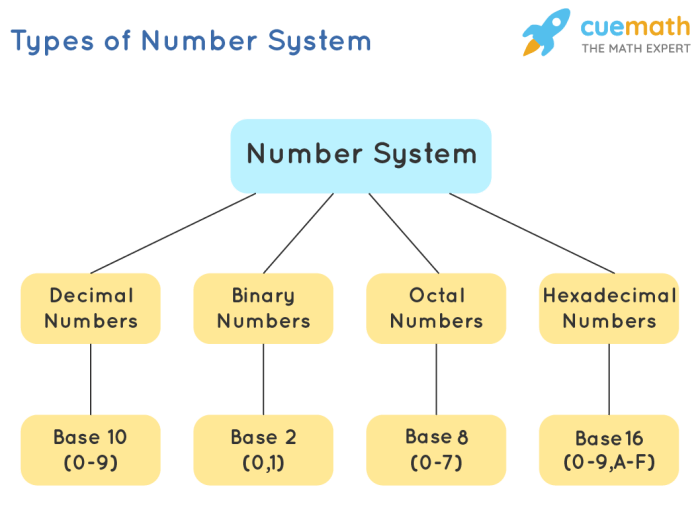
Konversi antar sistem bilangan merupakan proses mengubah representasi suatu nilai numerik dari satu sistem bilangan ke sistem bilangan lainnya. Proses ini penting dalam ilmu komputer karena komputer bekerja dengan sistem bilangan biner (basis 2), sedangkan manusia umumnya menggunakan sistem bilangan desimal (basis 10). Konversi antar sistem bilangan memungkinkan kita untuk memahami dan mengolah data yang diproses oleh komputer.
Konversi dari Desimal ke Biner
Untuk mengubah bilangan desimal ke biner, kita dapat menggunakan metode pembagian berulang dengan basis 2. Berikut langkah-langkahnya:
- Bagi bilangan desimal dengan 2. Catat hasil bagi dan sisanya.
- Bagi hasil bagi sebelumnya dengan 2 lagi. Catat hasil bagi dan sisanya.
- Ulangi langkah 2 hingga hasil bagi bernilai 0.
- Bilangan biner diperoleh dengan menuliskan sisa pembagian dari bawah ke atas.
Sebagai contoh, untuk mengubah bilangan desimal 13 ke biner:
| Pembagian | Hasil Bagi | Sisa |
|---|---|---|
| 13 / 2 | 6 | 1 |
| 6 / 2 | 3 | 0 |
| 3 / 2 | 1 | 1 |
| 1 / 2 | 0 | 1 |
Jadi, bilangan biner dari 13 adalah 1101.
Konversi dari Desimal ke Oktal
Konversi dari desimal ke oktal mirip dengan konversi ke biner, hanya saja kita menggunakan basis 8. Berikut langkah-langkahnya:
- Bagi bilangan desimal dengan 8. Catat hasil bagi dan sisanya.
- Bagi hasil bagi sebelumnya dengan 8 lagi. Catat hasil bagi dan sisanya.
- Ulangi langkah 2 hingga hasil bagi bernilai 0.
- Bilangan oktal diperoleh dengan menuliskan sisa pembagian dari bawah ke atas.
Contohnya, untuk mengubah bilangan desimal 25 ke oktal:
| Pembagian | Hasil Bagi | Sisa |
|---|---|---|
| 25 / 8 | 3 | 1 |
| 3 / 8 | 0 | 3 |
Jadi, bilangan oktal dari 25 adalah 31.
Konversi dari Desimal ke Heksadesimal
Konversi dari desimal ke heksadesimal juga menggunakan metode pembagian berulang, namun kali ini dengan basis 16. Karena heksadesimal menggunakan 16 digit (0-9 dan A-F), maka sisa pembagian yang lebih besar dari 9 diwakili oleh huruf A-F.
- Bagi bilangan desimal dengan 16. Catat hasil bagi dan sisanya.
- Bagi hasil bagi sebelumnya dengan 16 lagi. Catat hasil bagi dan sisanya.
- Ulangi langkah 2 hingga hasil bagi bernilai 0.
- Bilangan heksadesimal diperoleh dengan menuliskan sisa pembagian dari bawah ke atas, dengan mengganti sisa yang lebih besar dari 9 dengan huruf A-F.
Contohnya, untuk mengubah bilangan desimal 42 ke heksadesimal:
| Pembagian | Hasil Bagi | Sisa |
|---|---|---|
| 42 / 16 | 2 | 10 (A) |
| 2 / 16 | 0 | 2 |
Jadi, bilangan heksadesimal dari 42 adalah 2A.
Metode Konversi Antar Sistem Bilangan
Selain metode pembagian berulang, ada beberapa metode lain yang dapat digunakan untuk konversi antar sistem bilangan, seperti:
- Metode tabel konversi: Metode ini menggunakan tabel yang menunjukkan nilai ekivalen antara digit dalam berbagai sistem bilangan. Misalnya, tabel konversi desimal-biner menunjukkan nilai biner dari setiap digit desimal dari 0 hingga 9.
- Metode kalkulator: Kalkulator ilmiah atau kalkulator online dapat digunakan untuk melakukan konversi antar sistem bilangan dengan mudah.
- Metode program komputer: Program komputer khusus dapat digunakan untuk melakukan konversi antar sistem bilangan dengan cepat dan akurat.
Penerapan Sistem Bilangan dalam Komputer: Pengertian Sistem Bilangan Dalam Ilmu Komputer

Sistem bilangan merupakan fondasi utama dalam ilmu komputer, menjadi dasar dari semua operasi dan pengolahan data. Sistem bilangan ini berperan penting dalam berbagai komponen komputer, seperti CPU, memori, dan perangkat input/output. Pemahaman mengenai sistem bilangan sangat penting untuk memahami bagaimana komputer bekerja dan memproses informasi.
Peran Sistem Bilangan dalam Komponen Komputer
Sistem bilangan berperan penting dalam berbagai komponen komputer, terutama dalam hal representasi dan manipulasi data.
- CPU (Central Processing Unit): CPU menggunakan sistem bilangan biner (basis 2) untuk memproses instruksi dan data. Setiap instruksi dan data direpresentasikan sebagai serangkaian bit (0 dan 1), yang kemudian diproses oleh CPU untuk menghasilkan output.
- Memori: Memori komputer juga menggunakan sistem bilangan biner untuk menyimpan data. Setiap lokasi memori memiliki alamat unik yang direpresentasikan dalam bentuk bilangan biner. Data yang disimpan dalam memori juga direpresentasikan dalam bentuk biner.
- Perangkat Input/Output: Perangkat input/output seperti keyboard, mouse, dan monitor juga menggunakan sistem bilangan untuk berkomunikasi dengan komputer. Misalnya, keyboard mengubah karakter yang ditekan menjadi kode ASCII (American Standard Code for Information Interchange), yang merupakan sistem bilangan biner yang mewakili karakter tersebut.
Peran Sistem Bilangan dalam Pengolahan Data dan Eksekusi
Sistem bilangan memainkan peran penting dalam proses pengolahan data dan eksekusi instruksi di komputer. CPU memproses data dan instruksi yang direpresentasikan dalam bentuk bilangan biner. Data yang diproses dapat berupa angka, teks, gambar, atau suara. CPU menggunakan operasi aritmatika dan logika untuk memanipulasi data biner, menghasilkan output yang diinginkan.
Contoh Penerapan Sistem Bilangan dalam Pemrosesan Data Digital dan Komunikasi Data
Sistem bilangan biner digunakan secara luas dalam pemrosesan data digital dan komunikasi data. Berikut adalah beberapa contoh:
- Representasi Gambar: Gambar digital disimpan dalam bentuk piksel, dan setiap piksel direpresentasikan dengan nilai biner yang menentukan warna dan kecerahannya.
- Komunikasi Data: Data yang ditransmisikan melalui internet atau jaringan komputer direpresentasikan dalam bentuk biner. Sistem bilangan biner memungkinkan data untuk dipecah menjadi bit-bit yang dapat dikirimkan melalui kabel atau gelombang radio.
- Pemrosesan Audio: Suara digital juga disimpan dalam bentuk biner. Suara direkam dan diubah menjadi sinyal digital, yang kemudian dipecah menjadi bit-bit dan disimpan dalam bentuk biner.
Ringkasan Akhir

Sistem bilangan adalah kunci yang membuka pintu ke dunia komputasi. Memahami sistem bilangan berarti memahami bagaimana komputer berpikir dan berinteraksi dengan data. Dengan pemahaman yang mendalam tentang sistem bilangan, kita dapat lebih memahami cara kerja komputer dan bagaimana teknologi ini terus berkembang. Dari sistem bilangan biner yang sederhana hingga sistem bilangan heksadesimal yang lebih kompleks, setiap sistem memiliki peran penting dalam membangun dunia digital yang kita kenal saat ini.