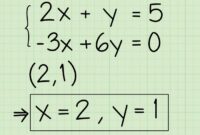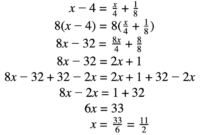Semester pertama kelas 10 adalah momen penting dalam perjalanan belajar matematika. Di sini, kamu akan bertemu dengan konsep-konsep baru yang lebih kompleks dan menantang. Rangkuman Materi Matematika Kelas 10 Semester 1 ini hadir untuk membantumu memahami materi dengan lebih mudah dan mendalam.
Dari aljabar hingga geometri, kamu akan menemukan berbagai topik yang saling terkait dan membentuk dasar pemahaman matematika tingkat lanjut. Setiap materi disajikan dengan penjelasan detail, contoh soal, dan strategi belajar yang efektif. Dengan memahami konsep dan rumus dengan baik, kamu siap untuk menghadapi tantangan matematika di masa depan.
Materi Matematika Kelas 10 Semester 1
Matematika kelas 10 semester 1 merupakan pondasi penting untuk memahami konsep-konsep matematika yang lebih kompleks di tingkat selanjutnya. Materi yang dipelajari meliputi aljabar, geometri, dan pengantar trigonometri. Materi ini membantu mengembangkan kemampuan berpikir logis, analitis, dan memecahkan masalah, yang bermanfaat dalam berbagai bidang kehidupan.
Aljabar
Aljabar merupakan cabang matematika yang mempelajari tentang simbol-simbol dan aturan-aturan yang digunakan untuk merepresentasikan dan menyelesaikan persamaan matematika. Materi aljabar di kelas 10 semester 1 meliputi:
- Operasi aljabar: Penjumlahan, pengurangan, perkalian, dan pembagian pada bentuk aljabar.
- Persamaan linear: Memahami konsep persamaan linear, cara menyelesaikan persamaan linear satu variabel dan dua variabel.
- Pertidaksamaan linear: Memahami konsep pertidaksamaan linear, cara menyelesaikan pertidaksamaan linear satu variabel dan dua variabel.
- Sistem persamaan linear: Memahami konsep sistem persamaan linear, cara menyelesaikan sistem persamaan linear dua variabel dengan metode substitusi, eliminasi, dan grafik.
Berikut contoh soal aljabar dan pembahasannya:
Tentukan penyelesaian dari persamaan linear 2x + 3 = 7.
Pembahasan:
- Kurangi kedua ruas persamaan dengan 3: 2x + 3 – 3 = 7 – 3
- Sederhanakan: 2x = 4
- Bagi kedua ruas persamaan dengan 2: 2x / 2 = 4 / 2
- Sederhanakan: x = 2
- Jadi, penyelesaian dari persamaan linear 2x + 3 = 7 adalah x = 2.
Geometri
Geometri merupakan cabang matematika yang mempelajari tentang bentuk, ukuran, dan posisi objek dalam ruang. Materi geometri di kelas 10 semester 1 meliputi:
- Bangun datar: Memahami jenis-jenis bangun datar, seperti segitiga, persegi panjang, lingkaran, dan lain-lain.
- Keliling dan luas bangun datar: Menghitung keliling dan luas bangun datar.
- Bangun ruang: Memahami jenis-jenis bangun ruang, seperti kubus, balok, prisma, limas, dan lain-lain.
- Volume dan luas permukaan bangun ruang: Menghitung volume dan luas permukaan bangun ruang.
Berikut contoh soal geometri dan pembahasannya:
Sebuah persegi panjang memiliki panjang 10 cm dan lebar 5 cm. Hitunglah keliling dan luas persegi panjang tersebut.
Pembahasan:
- Keliling persegi panjang = 2 x (panjang + lebar) = 2 x (10 cm + 5 cm) = 30 cm
- Luas persegi panjang = panjang x lebar = 10 cm x 5 cm = 50 cm2
- Jadi, keliling persegi panjang tersebut adalah 30 cm dan luasnya adalah 50 cm2.
Trigonometri
Trigonometri merupakan cabang matematika yang mempelajari tentang hubungan antara sudut dan sisi dalam segitiga siku-siku. Materi trigonometri di kelas 10 semester 1 meliputi:
- Perbandingan trigonometri: Memahami konsep sinus, cosinus, dan tangen dalam segitiga siku-siku.
- Rumus dasar trigonometri: Memahami dan menggunakan rumus dasar trigonometri, seperti rumus Pythagoras, rumus sudut berelasi, dan rumus sudut ganda.
- Penerapan trigonometri: Menerapkan konsep trigonometri untuk menyelesaikan masalah-masalah yang berkaitan dengan jarak, ketinggian, dan sudut.
Berikut contoh soal trigonometri dan pembahasannya:
Sebuah tangga dengan panjang 5 meter bersandar pada tembok. Jika sudut antara tangga dan tanah adalah 60 derajat, tentukan tinggi tembok yang dicapai tangga.
Pembahasan:
- Dalam segitiga siku-siku yang dibentuk oleh tangga, tembok, dan tanah, tinggi tembok merupakan sisi depan sudut 60 derajat, dan panjang tangga merupakan sisi miring.
- Maka, sin 60 derajat = tinggi tembok / panjang tangga
- Sin 60 derajat = √3 / 2
- Jadi, tinggi tembok = sin 60 derajat x panjang tangga = (√3 / 2) x 5 meter = 5√3 / 2 meter.
Diagram Alur Materi Matematika Kelas 10 Semester 1
Diagram alur berikut menunjukkan hubungan antar materi dalam matematika kelas 10 semester 1:
[Gambar Diagram Alur]
Diagram alur ini menunjukkan bahwa materi aljabar dan geometri merupakan dasar untuk mempelajari trigonometri. Ketiga materi ini saling terkait dan saling mendukung dalam pemahaman konsep-konsep matematika.
Rumus dan Konsep Penting
Matematika kelas 10 semester 1 merupakan fondasi penting untuk memahami konsep matematika yang lebih kompleks di masa depan. Materi ini mencakup berbagai topik yang saling terkait, sehingga penting untuk memahami rumus dan konsep kunci dalam setiap topik. Berikut adalah ringkasan rumus dan konsep penting yang perlu dipahami, diurutkan berdasarkan tingkat kesulitan dan urutan pembelajaran.
Fungsi
Fungsi merupakan salah satu konsep dasar dalam matematika. Fungsi menghubungkan setiap elemen dari suatu himpunan (domain) dengan tepat satu elemen dari himpunan lain (kodomain).
- Pengertian Fungsi: Relasi khusus yang memasangkan setiap anggota domain dengan tepat satu anggota kodomain.
- Jenis-jenis Fungsi: Fungsi linear, fungsi kuadrat, fungsi eksponen, fungsi logaritma, dan fungsi trigonometri.
- Menentukan Domain dan Range: Domain adalah himpunan semua nilai input yang mungkin, sedangkan range adalah himpunan semua nilai output yang mungkin.
- Grafik Fungsi: Representasi visual dari fungsi, menunjukkan hubungan antara nilai input dan output.
Contohnya, fungsi f(x) = 2x + 1 menghubungkan setiap nilai x dengan nilai 2x + 1. Jika x = 2, maka f(2) = 2(2) + 1 = 5. Grafik fungsi ini akan berupa garis lurus dengan kemiringan 2 dan memotong sumbu y di titik (0, 1).
Sistem Persamaan Linear Dua Variabel
Sistem persamaan linear dua variabel merupakan kumpulan dari dua persamaan linear yang memiliki dua variabel yang sama.
- Metode Penyelesaian: Metode substitusi, metode eliminasi, dan metode grafik.
- Solusi Sistem Persamaan: Pasangan nilai variabel yang memenuhi semua persamaan dalam sistem.
- Sistem Persamaan Linear Homogen: Sistem persamaan linear yang memiliki konstanta nol.
Contohnya, sistem persamaan linear: 2x + y = 5 dan x – y = 1. Solusi dari sistem persamaan ini adalah x = 2 dan y = 1, karena nilai ini memenuhi kedua persamaan.
Matriks
Matriks adalah susunan bilangan yang disusun dalam baris dan kolom. Matriks memiliki banyak aplikasi dalam matematika, seperti dalam menyelesaikan sistem persamaan linear, transformasi geometri, dan kalkulus linear.
- Pengertian Matriks: Susunan bilangan yang disusun dalam baris dan kolom.
- Operasi Matriks: Penjumlahan, pengurangan, perkalian, dan transpos.
- Determinan Matriks: Skalar yang berhubungan dengan matriks persegi.
- Invers Matriks: Matriks yang dikalikan dengan matriks awal menghasilkan matriks identitas.
Contohnya, matriks A = [1 2; 3 4] memiliki determinan 2. Invers dari matriks A adalah A-1 = [2 -1; -3 1].
Determinan dan Invers Matriks
Determinan dan invers matriks merupakan konsep penting dalam aljabar linear. Determinan digunakan untuk menentukan apakah matriks memiliki invers, sedangkan invers matriks digunakan untuk menyelesaikan sistem persamaan linear dan transformasi geometri.
- Determinan Matriks: Skalar yang berhubungan dengan matriks persegi.
- Invers Matriks: Matriks yang dikalikan dengan matriks awal menghasilkan matriks identitas.
- Sifat Determinan: Determinan matriks segitiga atas dan bawah, determinan matriks identitas, dan determinan matriks singular.
- Mencari Invers Matriks: Metode adjoin dan metode Gauss-Jordan.
Contohnya, determinan matriks A = [1 2; 3 4] adalah 2. Invers dari matriks A adalah A-1 = [2 -1; -3 1].
Transformasi Geometri
Transformasi geometri merupakan perubahan posisi atau bentuk suatu objek geometri.
- Jenis-jenis Transformasi: Translasi, rotasi, refleksi, dan dilatasi.
- Matriks Transformasi: Matriks yang digunakan untuk merepresentasikan transformasi geometri.
- Komposisi Transformasi: Gabungan dari beberapa transformasi.
Contohnya, translasi 2 satuan ke kanan dan 3 satuan ke atas dapat direpresentasikan dengan matriks transformasi [1 0; 0 1] + [2; 3].
Statistika, Rangkuman materi matematika kelas 10 semester 1
Statistika merupakan ilmu yang mempelajari tentang pengumpulan, pengolahan, analisis, interpretasi, dan penyajian data.
- Ukuran Pemusatan Data: Mean, median, dan modus.
- Ukuran Penyebaran Data: Ragam, simpangan baku, dan jangkauan.
- Presentasi Data: Diagram batang, diagram lingkaran, dan histogram.
Contohnya, data tinggi badan siswa kelas 10 adalah 160 cm, 165 cm, 170 cm, 175 cm, dan 180 cm. Mean dari data ini adalah 170 cm, mediannya adalah 170 cm, dan modusnya adalah 170 cm.
Strategi Mempelajari Matematika

Matematika di kelas 10 semester 1 memang menantang, tetapi dengan strategi belajar yang tepat, kamu bisa menaklukkannya dengan mudah! Berikut beberapa tips dan strategi yang bisa kamu terapkan untuk memahami konsep dan rumus matematika dengan cepat dan efektif.
Memahami Konsep
Memahami konsep dasar adalah kunci untuk mempelajari matematika. Jangan hanya menghafal rumus, tapi pahami bagaimana rumus tersebut diturunkan dan apa makna di baliknya. Kamu bisa melakukan hal berikut:
- Baca buku teks dengan cermat dan fokus pada contoh-contoh yang diberikan.
- Buat catatan ringkas dengan bahasa kamu sendiri. Ini membantu kamu memahami konsep dengan lebih baik dan mudah diingat.
- Jangan ragu untuk bertanya kepada guru atau teman jika ada konsep yang belum dipahami.
- Cobalah untuk menjelaskan konsep kepada orang lain. Ini akan menguji pemahaman kamu dan membantu kamu mengingat dengan lebih baik.
Latihan Soal dan Pembahasan
Untuk menguji pemahaman dan kemampuan Anda dalam materi matematika kelas 10 semester 1, berikut ini disajikan beberapa latihan soal dengan pembahasan yang lengkap. Soal-soal ini dirancang untuk mencakup berbagai tingkat kesulitan, mulai dari yang mudah hingga yang menantang. Melalui latihan ini, Anda dapat mengasah kemampuan berpikir kritis dan pemecahan masalah dalam matematika.
Persamaan dan Pertidaksamaan Linear
Persamaan dan pertidaksamaan linear merupakan konsep dasar dalam matematika yang penting untuk dipahami. Berikut ini beberapa soal latihan yang dapat Anda kerjakan:
| No. | Soal | Pembahasan |
|---|---|---|
| 1 | Tentukan himpunan penyelesaian dari persamaan 2x + 3 = 7. |
Langkah pertama adalah mengisolasi variabel x. Untuk melakukannya, kita kurangi kedua ruas dengan 3:
Maka diperoleh:
Kemudian, bagi kedua ruas dengan 2:
Sehingga diperoleh:
Jadi, himpunan penyelesaian dari persamaan 2x + 3 = 7 adalah 2. |
| 2 | Tentukan himpunan penyelesaian dari pertidaksamaan 3x – 5 < 10. |
Langkah pertama adalah mengisolasi variabel x. Untuk melakukannya, kita tambahkan 5 ke kedua ruas:
Maka diperoleh:
Kemudian, bagi kedua ruas dengan 3:
Sehingga diperoleh:
Jadi, himpunan penyelesaian dari pertidaksamaan 3x – 5 < 10 adalah x | x < 5. |
Sistem Persamaan Linear Dua Variabel
Sistem persamaan linear dua variabel merupakan sistem persamaan yang melibatkan dua variabel dan dua persamaan. Berikut ini beberapa soal latihan yang dapat Anda kerjakan:
| No. | Soal | Pembahasan |
|---|---|---|
| 1 | Tentukan himpunan penyelesaian dari sistem persamaan berikut: 2x + y = 5 x – y = 1 |
Ada beberapa metode untuk menyelesaikan sistem persamaan linear dua variabel, salah satunya adalah metode eliminasi. Metode eliminasi dilakukan dengan menghilangkan salah satu variabel dengan cara menjumlahkan atau mengurangkan kedua persamaan. Dalam kasus ini, kita dapat langsung menjumlahkan kedua persamaan:
Maka diperoleh:
Kemudian, bagi kedua ruas dengan 3:
Sehingga diperoleh:
Selanjutnya, kita substitusikan nilai x = 2 ke salah satu persamaan, misalnya persamaan 2x + y = 5:
Maka diperoleh:
Kemudian, kurangi kedua ruas dengan 4:
Sehingga diperoleh:
Jadi, himpunan penyelesaian dari sistem persamaan 2x + y = 5 dan x – y = 1 adalah (2, 1). |
Fungsi Linear
Fungsi linear merupakan fungsi yang grafiknya berupa garis lurus. Berikut ini beberapa soal latihan yang dapat Anda kerjakan:
| No. | Soal | Pembahasan |
|---|---|---|
| 1 | Tentukan persamaan garis lurus yang melalui titik (2, 3) dan (4, 5). |
Persamaan garis lurus dapat ditulis dalam bentuk y = mx + c, dimana m adalah gradien dan c adalah konstanta. Untuk menentukan persamaan garis lurus yang melalui dua titik, kita perlu mencari gradiennya terlebih dahulu. Gradien dapat dihitung dengan rumus:
Dalam kasus ini, x1 = 2, y1 = 3, x2 = 4, dan y2 = 5. Maka, gradiennya adalah:
Selanjutnya, kita substitusikan nilai m = 1 dan salah satu titik, misalnya (2, 3), ke persamaan y = mx + c:
Maka diperoleh:
Kemudian, kurangi kedua ruas dengan 2:
Sehingga diperoleh:
Jadi, persamaan garis lurus yang melalui titik (2, 3) dan (4, 5) adalah y = x + 1. |
Sistem Pertidaksamaan Linear Dua Variabel
Sistem pertidaksamaan linear dua variabel merupakan sistem pertidaksamaan yang melibatkan dua variabel dan dua atau lebih pertidaksamaan. Berikut ini beberapa soal latihan yang dapat Anda kerjakan:
| No. | Soal | Pembahasan |
|---|---|---|
| 1 | Tentukan daerah penyelesaian dari sistem pertidaksamaan berikut: x + y <= 6 2x – y >= 2 x >= 0 y >= 0 |
Untuk menentukan daerah penyelesaian dari sistem pertidaksamaan linear dua variabel, kita perlu menggambar grafik dari setiap pertidaksamaan dan menentukan daerah yang memenuhi semua pertidaksamaan. Langkah pertama adalah menggambar grafik dari pertidaksamaan x + y <= 6. Untuk menggambar grafiknya, kita perlu menentukan titik potong dengan sumbu x dan sumbu y. Titik potong dengan sumbu x diperoleh dengan mensubstitusikan y = 0 ke pertidaksamaan, sehingga diperoleh x = 6. Titik potong dengan sumbu y diperoleh dengan mensubstitusikan x = 0 ke pertidaksamaan, sehingga diperoleh y = 6. Kemudian, kita hubungkan kedua titik tersebut dengan garis lurus. Karena pertidaksamaan adalah <=, maka daerah yang memenuhi pertidaksamaan adalah daerah di bawah garis lurus. Selanjutnya, kita menggambar grafik dari pertidaksamaan 2x – y >= 2. Titik potong dengan sumbu x diperoleh dengan mensubstitusikan y = 0 ke pertidaksamaan, sehingga diperoleh x = 1. Titik potong dengan sumbu y diperoleh dengan mensubstitusikan x = 0 ke pertidaksamaan, sehingga diperoleh y = -2. Kemudian, kita hubungkan kedua titik tersebut dengan garis lurus. Karena pertidaksamaan adalah >=, maka daerah yang memenuhi pertidaksamaan adalah daerah di atas garis lurus. Kemudian, kita menggambar grafik dari pertidaksamaan x >= 0. Grafik dari pertidaksamaan ini adalah garis vertikal yang melalui titik (0, 0) dan semua titik di sebelah kanan garis tersebut. Karena pertidaksamaan adalah >=, maka daerah yang memenuhi pertidaksamaan adalah daerah di sebelah kanan garis lurus. Terakhir, kita menggambar grafik dari pertidaksamaan y >= 0. Grafik dari pertidaksamaan ini adalah garis horizontal yang melalui titik (0, 0) dan semua titik di atas garis tersebut. Karena pertidaksamaan adalah >=, maka daerah yang memenuhi pertidaksamaan adalah daerah di atas garis lurus. Daerah penyelesaian dari sistem pertidaksamaan adalah daerah yang memenuhi semua pertidaksamaan, yaitu daerah yang diarsir pada gambar. |
Matriks
Matriks merupakan susunan bilangan yang disusun dalam baris dan kolom. Berikut ini beberapa soal latihan yang dapat Anda kerjakan:
| No. | Soal | Pembahasan |
|---|---|---|
| 1 | Tentukan hasil penjumlahan dari matriks A dan B berikut: A = [ 1 2 ] [ 3 4 ] B = [ 5 6 ] [ 7 8 ] |
Penjumlahan matriks dilakukan dengan menjumlahkan elemen-elemen yang seletak. Maka, hasil penjumlahan dari matriks A dan B adalah:
|
Determinan Matriks
Determinan matriks merupakan nilai skalar yang dihitung dari matriks persegi. Berikut ini beberapa soal latihan yang dapat Anda kerjakan:
| No. | Soal | Pembahasan |
|---|---|---|
| 1 | Tentukan determinan dari matriks A berikut: A = [ 2 3 ] [ 4 5 ] |
Determinan dari matriks 2×2 dapat dihitung dengan rumus:
Dalam kasus ini, a = 2, b = 3, c = 4, dan d = 5. Maka, determinan dari matriks A adalah:
|
Invers Matriks
Invers matriks merupakan matriks yang jika dikalikan dengan matriks aslinya akan menghasilkan matriks identitas. Berikut ini beberapa soal latihan yang dapat Anda kerjakan:
| No. | Soal | Pembahasan |
|---|---|---|
| 1 | Tentukan invers dari matriks A berikut: A = [ 2 1 ] [ 4 3 ] |
Invers dari matriks 2×2 dapat dihitung dengan rumus:
Dalam kasus ini, a = 2, b = 1, c = 4, dan d = 3. Maka, determinan dari matriks A adalah:
Sehingga, invers dari matriks A adalah:
|
Transformasi Geometri
Transformasi geometri merupakan perubahan posisi atau bentuk suatu objek geometri. Berikut ini beberapa soal latihan yang dapat Anda kerjakan:
| No. | Soal | Pembahasan |
|---|---|---|
| 1 | Tentukan bayangan titik A(2, 3) setelah ditranslasikan oleh vektor T = (1, -2). |
Translasi adalah pergeseran suatu objek geometri dengan vektor tertentu. Bayangan titik A setelah ditranslasikan oleh vektor T dapat dihitung dengan rumus:
Dalam kasus ini, A = (2, 3) dan T = (1, -2). Maka, bayangan titik A adalah:
Jadi, bayangan titik A(2, 3) setelah ditranslasikan oleh vektor T = (1, -2) adalah A'(3, 1). |
Penerapan Matematika dalam Kehidupan Sehari-hari
Matematika, seringkali dianggap sebagai mata pelajaran yang rumit dan hanya bermanfaat untuk bidang-bidang tertentu, nyatanya memiliki peran penting dalam kehidupan sehari-hari. Materi matematika yang dipelajari di kelas 10 semester 1, seperti persamaan linear, fungsi, dan geometri, memiliki aplikasi yang luas dan tak terduga dalam berbagai aspek kehidupan.
Contoh Penerapan Matematika dalam Kehidupan Sehari-hari
Matematika membantu kita dalam berbagai aspek kehidupan sehari-hari, dari perencanaan keuangan hingga memahami pola alam. Contohnya, saat berbelanja, kita menggunakan perhitungan untuk membandingkan harga dan memilih produk terbaik. Saat memasak, kita menggunakan konsep perbandingan untuk menentukan takaran bahan. Dalam olahraga, kita menggunakan matematika untuk menghitung kecepatan, jarak, dan waktu.
Manfaat Mempelajari Matematika untuk Berbagai Bidang
Mempelajari matematika tidak hanya bermanfaat untuk kehidupan sehari-hari, tetapi juga membuka peluang di berbagai bidang, seperti sains, teknologi, ekonomi, dan sosial.
- Sains: Matematika merupakan bahasa sains. Konsep matematika seperti kalkulus dan statistik digunakan untuk memahami dan menjelaskan fenomena alam. Contohnya, dalam fisika, matematika digunakan untuk memahami hukum gravitasi dan pergerakan benda.
- Teknologi: Matematika berperan penting dalam pengembangan teknologi. Konsep seperti aljabar dan geometri digunakan dalam desain perangkat lunak, arsitektur, dan robotika. Contohnya, algoritma yang digunakan dalam perangkat lunak komputer didasarkan pada konsep matematika.
- Ekonomi: Matematika digunakan untuk menganalisis data ekonomi, memprediksi tren pasar, dan mengelola keuangan. Contohnya, teori permainan dalam matematika digunakan untuk memahami perilaku konsumen dan strategi bisnis.
- Sosial: Matematika dapat digunakan untuk memahami pola sosial dan menyelesaikan masalah sosial. Contohnya, analisis data demografi menggunakan konsep statistik untuk memahami distribusi penduduk dan mengidentifikasi tren sosial.
Tabel Contoh Penerapan Matematika dalam Kehidupan Sehari-hari
| Contoh Penerapan | Bidang | Manfaat |
|---|---|---|
| Membuat anggaran bulanan | Keuangan | Membantu dalam mengatur pengeluaran dan mencapai tujuan keuangan |
| Menghitung kecepatan dan jarak saat berkendara | Transportasi | Membantu dalam merencanakan perjalanan dan menghindari keterlambatan |
| Mendesain bangunan | Arsitektur | Membantu dalam menciptakan struktur yang kokoh dan estetis |
| Menganalisis data penelitian | Sains | Membantu dalam memahami hasil penelitian dan menarik kesimpulan yang valid |
Matematika untuk Memecahkan Masalah dan Membuat Keputusan yang Lebih Baik
Matematika memberikan kerangka kerja yang sistematis untuk memecahkan masalah dan membuat keputusan yang lebih baik. Dengan menggunakan logika dan penalaran matematis, kita dapat menganalisis situasi, mengidentifikasi pola, dan menemukan solusi yang optimal. Contohnya, dalam bisnis, analisis data penjualan menggunakan konsep statistik dapat membantu dalam menentukan strategi pemasaran yang efektif.
Ringkasan Terakhir: Rangkuman Materi Matematika Kelas 10 Semester 1

Mempelajari matematika tidak hanya tentang menghafal rumus, tetapi juga tentang memahami konsep dan menerapkannya dalam berbagai situasi. Rangkuman Materi Matematika Kelas 10 Semester 1 ini akan menjadi panduan yang tepat untuk membangun fondasi yang kuat dalam matematika. Dengan tekun belajar dan berlatih, kamu akan mampu menguasai materi dengan baik dan membuka pintu menuju peluang baru di masa depan.