Trigonometri contoh soal – Trigonometri, cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga, sering kali terasa rumit. Namun, dengan memahami konsep dasarnya dan latihan yang cukup, trigonometri bisa menjadi topik yang menarik dan mudah dipahami. Dalam artikel ini, kita akan menjelajahi dunia trigonometri dengan contoh soal yang akan membantu Anda menguasai konsep dan memecahkan berbagai masalah.
Dari definisi trigonometri hingga penerapannya dalam kehidupan sehari-hari, kita akan membahas berbagai aspek penting yang perlu Anda ketahui. Dengan contoh soal yang terstruktur, Anda akan dapat melihat bagaimana teori trigonometri diterapkan dalam praktik, sehingga pemahaman Anda semakin kuat.
Pengertian Trigonometri
Trigonometri merupakan cabang matematika yang mempelajari hubungan antara sudut dan sisi-sisi dalam segitiga, terutama segitiga siku-siku. Trigonometri memiliki peran penting dalam berbagai bidang, seperti fisika, teknik, astronomi, dan navigasi.
Trigonometri, cabang matematika yang mempelajari hubungan antara sudut dan sisi segitiga, seringkali dijumpai dalam bentuk contoh soal. Misalnya, “Hitunglah panjang sisi miring segitiga siku-siku dengan sudut 30 derajat dan sisi alas 5 cm”. Untuk mengasah kemampuan persuasi dalam menulis, kamu juga bisa berlatih dengan contoh soal teks persuasi.
Contohnya, “Bujuklah temanmu untuk belajar trigonometri dengan menunjukkan manfaatnya dalam kehidupan sehari-hari”. Dengan berlatih, kamu akan semakin mahir dalam memahami konsep trigonometri dan mengaplikasikannya dalam berbagai situasi.
Hubungan Trigonometri dengan Segitiga Siku-siku
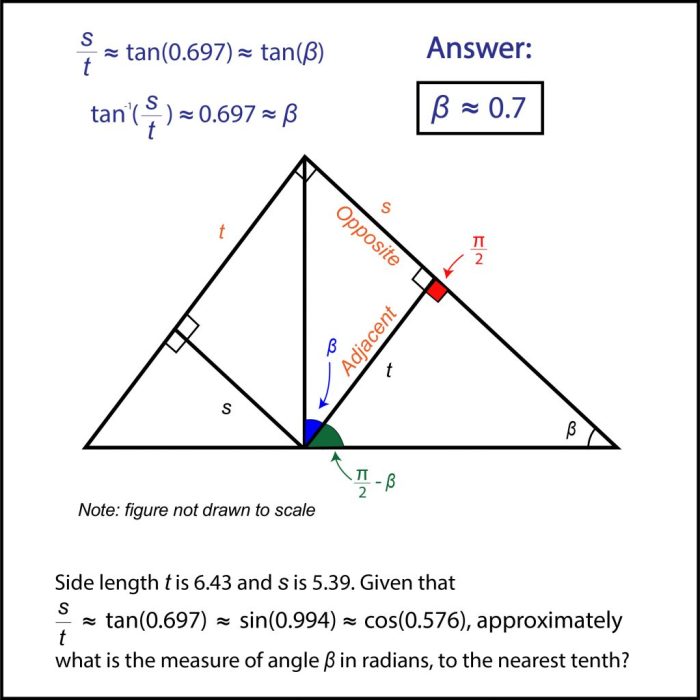
Trigonometri secara khusus berkaitan dengan segitiga siku-siku. Segitiga siku-siku adalah segitiga yang memiliki satu sudut siku-siku (90 derajat). Dalam segitiga siku-siku, terdapat tiga sisi utama: sisi miring (hipotenusa), sisi depan (opposite), dan sisi samping (adjacent) terhadap sudut yang sedang dikaji.
Konsep Dasar Trigonometri
Konsep dasar trigonometri melibatkan sudut, sisi, dan rasio trigonometri. Berikut adalah penjelasannya:
- Sudut: Sudut dalam trigonometri diukur dalam derajat atau radian. Sudut biasanya dilambangkan dengan huruf Yunani, seperti θ (theta).
- Sisi: Seperti yang telah dijelaskan, sisi dalam segitiga siku-siku dibagi menjadi sisi miring (hipotenusa), sisi depan (opposite), dan sisi samping (adjacent) terhadap sudut yang sedang dikaji.
- Rasio Trigonometri: Rasio trigonometri adalah hubungan antara sisi-sisi dalam segitiga siku-siku. Terdapat enam rasio trigonometri utama:
- Sinus (sin): Sin θ = Sisi depan / Sisi miring
- Cosinus (cos): Cos θ = Sisi samping / Sisi miring
- Tangen (tan): Tan θ = Sisi depan / Sisi samping
- Cosecan (csc): Csc θ = Sisi miring / Sisi depan
- Secan (sec): Sec θ = Sisi miring / Sisi samping
- Cotangen (cot): Cot θ = Sisi samping / Sisi depan
Contoh Sederhana Trigonometri
Misalnya, perhatikan segitiga siku-siku dengan sudut θ, sisi depan 3 cm, sisi samping 4 cm, dan sisi miring 5 cm. Maka, kita dapat menghitung rasio trigonometri untuk sudut θ:
- Sin θ = Sisi depan / Sisi miring = 3/5
- Cos θ = Sisi samping / Sisi miring = 4/5
- Tan θ = Sisi depan / Sisi samping = 3/4
Dengan memahami konsep dasar trigonometri, kita dapat menyelesaikan berbagai masalah yang melibatkan sudut, sisi, dan hubungan antar keduanya. Dalam aplikasi praktis, trigonometri membantu dalam menghitung jarak, tinggi, dan sudut dalam berbagai bidang seperti arsitektur, navigasi, dan astronomi.
Rasio Trigonometri: Trigonometri Contoh Soal
Dalam trigonometri, rasio trigonometri merupakan hubungan antara sisi-sisi suatu segitiga siku-siku dengan sudut-sudutnya. Rasio-rasio ini sangat penting dalam memahami dan menyelesaikan masalah yang melibatkan sudut dan sisi segitiga siku-siku.
Keenam Rasio Trigonometri, Trigonometri contoh soal
Ada enam rasio trigonometri utama yang perlu dipahami, yaitu:
- Sinus (sin)
- Cosinus (cos)
- Tangen (tan)
- Cosecan (csc)
- Secan (sec)
- Cotangen (cot)
Rumus Rasio Trigonometri
Setiap rasio trigonometri didefinisikan sebagai perbandingan antara dua sisi segitiga siku-siku. Berikut adalah rumus untuk menghitung setiap rasio trigonometri:
| Rasio | Rumus |
|---|---|
| Sinus (sin) | sin θ = Sisi Depan / Sisi Miring |
| Cosinus (cos) | cos θ = Sisi Samping / Sisi Miring |
| Tangen (tan) | tan θ = Sisi Depan / Sisi Samping |
| Cosecan (csc) | csc θ = Sisi Miring / Sisi Depan |
| Secan (sec) | sec θ = Sisi Miring / Sisi Samping |
| Cotangen (cot) | cot θ = Sisi Samping / Sisi Depan |
Contoh Soal
Misalkan kita memiliki segitiga siku-siku dengan sudut θ. Sisi depan dari sudut θ adalah 3 cm, sisi samping adalah 4 cm, dan sisi miring adalah 5 cm. Kita dapat menghitung nilai rasio trigonometri untuk sudut θ sebagai berikut:
- sin θ = Sisi Depan / Sisi Miring = 3 cm / 5 cm = 0.6
- cos θ = Sisi Samping / Sisi Miring = 4 cm / 5 cm = 0.8
- tan θ = Sisi Depan / Sisi Samping = 3 cm / 4 cm = 0.75
- csc θ = Sisi Miring / Sisi Depan = 5 cm / 3 cm = 1.67
- sec θ = Sisi Miring / Sisi Samping = 5 cm / 4 cm = 1.25
- cot θ = Sisi Samping / Sisi Depan = 4 cm / 3 cm = 1.33
Sudut Istimewa
Dalam trigonometri, sudut istimewa adalah sudut-sudut yang memiliki nilai sinus, cosinus, dan tangen yang mudah diingat dan sering digunakan dalam berbagai aplikasi. Sudut-sudut istimewa ini penting karena nilai-nilai trigonometrinya dapat dihitung dengan tepat tanpa menggunakan kalkulator. Sudut istimewa dalam trigonometri adalah 0°, 30°, 45°, 60°, dan 90°.
Nilai Rasio Trigonometri untuk Sudut Istimewa
Berikut adalah nilai rasio trigonometri untuk setiap sudut istimewa:
| Sudut | Sinus | Cosinus | Tangen |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | 1/2 | √3/2 | 1/√3 |
| 45° | √2/2 | √2/2 | 1 |
| 60° | √3/2 | 1/2 | √3 |
| 90° | 1 | 0 | ∞ |
Akhir Kata
Dengan memahami konsep trigonometri, Anda membuka pintu menuju berbagai bidang ilmu dan aplikasi. Dari arsitektur hingga navigasi, trigonometri memainkan peran penting dalam menyelesaikan masalah-masalah kompleks. Melalui contoh soal yang telah dibahas, diharapkan Anda dapat lebih percaya diri dalam menghadapi soal-soal trigonometri dan merasakan manfaatnya dalam kehidupan sehari-hari.





