Vektor Matematika Kelas 11, sebuah topik yang mungkin terdengar menakutkan, tetapi sebenarnya merupakan alat yang ampuh untuk memahami dunia di sekitar kita. Bayangkan Anda sedang mengarahkan pesawat terbang, atau mendesain bangunan tinggi. Vektor adalah kunci untuk menentukan arah, kecepatan, dan posisi objek-objek tersebut dengan presisi.
Di kelas 11, kita akan mempelajari dasar-dasar vektor, mulai dari pengertian dan cara menuliskannya, hingga operasi-operasi yang dapat dilakukan dengan vektor, seperti penjumlahan, pengurangan, dan perkalian. Kita juga akan mempelajari konsep-konsep penting seperti panjang vektor, vektor posisi, dan perkalian dot dan cross vektor. Semua konsep ini akan membantu kita memahami berbagai aplikasi vektor dalam geometri, fisika, dan bidang lainnya.
Pengertian Vektor
Dalam matematika kelas 11, vektor adalah besaran yang memiliki nilai dan arah. Bayangkan sebuah panah yang memiliki panjang tertentu dan menunjuk ke arah tertentu. Panah ini merepresentasikan vektor. Panjang panah mewakili besarnya vektor, dan arah panah menunjukkan arah vektor. Vektor berperan penting dalam berbagai bidang, seperti fisika, teknik, dan ilmu komputer.
Perbedaan Vektor dan Skalar
Vektor dan skalar adalah dua jenis besaran yang berbeda. Skalar hanya memiliki nilai, sedangkan vektor memiliki nilai dan arah. Misalnya, suhu adalah skalar, karena hanya memiliki nilai (misalnya 25 derajat Celcius). Namun, kecepatan adalah vektor, karena memiliki nilai (misalnya 10 meter per detik) dan arah (misalnya ke timur).
Cara Menuliskan Vektor
Vektor dapat dituliskan dalam beberapa bentuk, antara lain:
- Bentuk Koordinat: Vektor dituliskan sebagai pasangan terurut, yang menunjukkan koordinat titik ujung vektor. Misalnya, vektor v = (2, 3) menunjukkan bahwa titik ujung vektor berada di koordinat (2, 3).
- Bentuk Kolom: Vektor dituliskan sebagai matriks kolom, yang berisi komponen-komponen vektor. Misalnya, vektor v = (2, 3) dapat dituliskan dalam bentuk kolom sebagai:
[2]
[3]
Operasi Vektor
Vektor merupakan besaran yang memiliki nilai dan arah. Operasi vektor adalah manipulasi vektor untuk mendapatkan vektor baru atau informasi baru tentang vektor yang ada. Ada beberapa operasi vektor yang umum digunakan dalam matematika, yaitu penjumlahan, pengurangan, dan perkalian dengan skalar. Operasi-operasi ini memiliki aplikasi luas dalam berbagai bidang, seperti fisika, teknik, dan ilmu komputer.
Penjumlahan Vektor, Vektor matematika kelas 11
Penjumlahan vektor adalah operasi yang menggabungkan dua vektor untuk menghasilkan vektor baru yang disebut vektor resultan. Vektor resultan memiliki besar dan arah yang ditentukan oleh penjumlahan vektor-vektor yang dijumlahkan. Secara geometris, penjumlahan vektor dapat digambarkan dengan metode jajar genjang atau metode segitiga.
- Metode Jajar Genjang: Jika dua vektor, a dan b, diwakili oleh sisi-sisi jajar genjang, maka vektor resultan a + b diwakili oleh diagonal jajar genjang yang berlawanan dengan titik awal a dan b. Ilustrasi: [Gambar jajar genjang dengan sisi a dan b, diagonalnya adalah a + b].
- Metode Segitiga: Jika dua vektor, a dan b, diwakili oleh dua sisi segitiga yang berurutan, maka vektor resultan a + b diwakili oleh sisi ketiga segitiga tersebut. Ilustrasi: [Gambar segitiga dengan sisi a dan b, sisi ketiga adalah a + b].
Pengurangan Vektor
Pengurangan vektor adalah operasi yang menentukan selisih antara dua vektor. Secara geometris, pengurangan vektor dapat diinterpretasikan sebagai penjumlahan vektor pertama dengan vektor negatif dari vektor kedua. Vektor negatif dari suatu vektor memiliki besar yang sama tetapi arah yang berlawanan.
- Metode Segitiga: Jika dua vektor, a dan b, diwakili oleh dua sisi segitiga yang berurutan, maka vektor resultan a – b diwakili oleh sisi ketiga segitiga tersebut, dengan arah dari b ke a. Ilustrasi: [Gambar segitiga dengan sisi a dan -b, sisi ketiga adalah a – b].
Perkalian Vektor dengan Skalar
Perkalian vektor dengan skalar adalah operasi yang mengalikan vektor dengan suatu bilangan real (skalar). Hasilnya adalah vektor baru dengan besar yang dikalikan dengan skalar tersebut, dan arahnya sama dengan vektor awal jika skalar positif, dan berlawanan arah jika skalar negatif.
- Ilustrasi: Jika a adalah vektor dan k adalah skalar, maka ka adalah vektor baru dengan besar k|a| dan arah yang sama dengan a jika k positif, atau berlawanan arah dengan a jika k negatif. Ilustrasi: [Gambar vektor a dan ka, dengan k positif dan negatif].
Rumus dan Contoh Operasi Vektor
| Operasi | Rumus | Contoh |
|---|---|---|
| Penjumlahan | a + b = (a1 + b1, a2 + b2) | Jika a = (2, 3) dan b = (1, -1), maka a + b = (2 + 1, 3 – 1) = (3, 2). |
| Pengurangan | a – b = (a1 – b1, a2 – b2) | Jika a = (2, 3) dan b = (1, -1), maka a – b = (2 – 1, 3 + 1) = (1, 4). |
| Perkalian dengan Skalar | ka = (ka1, ka2) | Jika a = (2, 3) dan k = 2, maka ka = (2 * 2, 2 * 3) = (4, 6). |
Panjang Vektor
Panjang vektor merupakan besaran skalar yang menunjukkan jarak dari titik pangkal vektor ke titik ujungnya. Panjang vektor dapat dihitung menggunakan rumus Pythagoras, dengan mempertimbangkan vektor sebagai sisi miring dari segitiga siku-siku.
Menentukan Panjang Vektor
Panjang vektor $\overrightarrowa = (a_1, a_2, a_3)$ dapat ditentukan dengan menggunakan rumus berikut:
$|\overrightarrowa| = \sqrta_1^2 + a_2^2 + a_3^2$
Contohnya, jika $\overrightarrowa = (3, 4, 0)$, maka panjang vektor $\overrightarrowa$ adalah:
$|\overrightarrowa| = \sqrt3^2 + 4^2 + 0^2 = \sqrt25 = 5$
Jadi, panjang vektor $\overrightarrowa$ adalah 5 satuan.
Vektor Satuan
Vektor satuan adalah vektor yang memiliki panjang satu satuan. Vektor satuan dapat ditentukan dengan membagi vektor dengan panjangnya. Vektor satuan dari vektor $\overrightarrowa$ dinotasikan sebagai $\hata$ dan dirumuskan sebagai berikut:
$\hata = \frac\overrightarrowa|\overrightarrowa|$
Contohnya, jika $\overrightarrowa = (3, 4, 0)$, maka vektor satuan $\hata$ adalah:
$\hata = \frac(3, 4, 0)\sqrt3^2 + 4^2 + 0^2 = \frac(3, 4, 0)5 = (\frac35, \frac45, 0)$
Jadi, vektor satuan dari $\overrightarrowa$ adalah $(\frac35, \frac45, 0)$.
Menentukan Vektor Searah
Dua vektor dikatakan searah jika keduanya memiliki arah yang sama. Vektor yang searah dengan vektor $\overrightarrowa$ dapat ditentukan dengan mengalikan $\overrightarrowa$ dengan suatu skalar. Skalar positif menunjukkan bahwa vektor searah dengan $\overrightarrowa$, sedangkan skalar negatif menunjukkan bahwa vektor berlawanan arah dengan $\overrightarrowa$.
Contohnya, jika $\overrightarrowa = (3, 4, 0)$, maka vektor yang searah dengan $\overrightarrowa$ adalah:
- $2\overrightarrowa = 2(3, 4, 0) = (6, 8, 0)$
- $-3\overrightarrowa = -3(3, 4, 0) = (-9, -12, 0)$
Vektor $(6, 8, 0)$ searah dengan $\overrightarrowa$, sedangkan vektor $(-9, -12, 0)$ berlawanan arah dengan $\overrightarrowa$.
Vektor Posisi

Vektor posisi adalah vektor yang menunjukkan lokasi suatu titik dalam ruang relatif terhadap titik acuan atau titik asal. Bayangkan kamu berada di sebuah lapangan, dan kamu ingin menunjukkan posisi temanmu yang sedang berdiri di lapangan tersebut. Kamu bisa menggunakan vektor posisi untuk menggambarkan lokasi temanmu dengan tepat.
Menentukan Vektor Posisi
Untuk menentukan vektor posisi suatu titik, kita perlu mengetahui titik asal dan koordinat titik tersebut. Misalnya, titik asal (0,0) dan titik A(3,4) dalam bidang dua dimensi. Vektor posisi titik A, yang kita tulis sebagai OA, dapat digambarkan sebagai garis berarah yang menghubungkan titik asal O ke titik A. Vektor ini memiliki komponen (3,4) karena pergeseran titik A dari titik asal adalah 3 satuan ke arah sumbu x dan 4 satuan ke arah sumbu y.
Menentukan Vektor Posisi dari Dua Titik
Vektor posisi dapat juga ditentukan dari dua titik yang diketahui. Misalnya, kita ingin menentukan vektor posisi AB dari titik A(2,1) ke titik B(5,3). Vektor AB dapat diperoleh dengan mengurangkan vektor posisi titik A dari vektor posisi titik B:
AB = OB – OA
Dengan demikian, vektor posisi AB adalah (5-2, 3-1) = (3,2).
Menentukan Jarak Antara Dua Titik Menggunakan Vektor Posisi
Jarak antara dua titik dapat ditentukan dengan menghitung panjang vektor posisi yang menghubungkan kedua titik tersebut. Panjang vektor posisi dapat dihitung dengan menggunakan teorema Pythagoras.
Misalnya, kita ingin menghitung jarak antara titik A(2,1) dan titik B(5,3). Vektor posisi AB adalah (3,2). Panjang vektor AB, yang merupakan jarak antara titik A dan B, dapat dihitung dengan rumus:
|AB| = √(3² + 2²) = √13
Jadi, jarak antara titik A dan B adalah √13 satuan.
Perkalian Dot Vektor: Vektor Matematika Kelas 11
Perkalian dot vektor, juga dikenal sebagai produk skalar, merupakan operasi yang menghasilkan skalar dari dua vektor. Hasil dari perkalian dot vektor ini sangat berguna dalam berbagai aplikasi, seperti menghitung proyeksi vektor, menghitung kerja yang dilakukan oleh gaya, dan mencari sudut antara dua vektor.
Pengertian Perkalian Dot Vektor
Perkalian dot vektor antara dua vektor, a dan b, didefinisikan sebagai perkalian panjang proyeksi a pada b dengan panjang b. Secara matematis, perkalian dot vektor ditulis sebagai a ⋅ b.
a ⋅ b = |a| |b| cos θ
di mana θ adalah sudut antara vektor a dan b.
Sebagai ilustrasi, bayangkan vektor a dan b pada bidang dua dimensi. Proyeksi a pada b adalah bayangan a yang dijatuhkan secara tegak lurus ke garis yang mengandung b. Perkalian dot vektor a ⋅ b adalah perkalian panjang proyeksi a pada b dengan panjang b.
Misalnya, jika a = (3, 4) dan b = (1, 2), maka panjang proyeksi a pada b adalah 3, dan panjang b adalah √5. Jadi, a ⋅ b = 3√5.
Sifat-sifat Perkalian Dot Vektor
Perkalian dot vektor memiliki beberapa sifat penting yang membuatnya mudah untuk dikerjakan. Berikut beberapa sifat tersebut:
- Komutatif: a ⋅ b = b ⋅ a. Urutan perkalian tidak berpengaruh pada hasil.
- Distributif: a ⋅ (b + c) = a ⋅ b + a ⋅ c. Perkalian dot dapat didistribusikan terhadap penjumlahan vektor.
- Skalar: (ka) ⋅ b = k(a ⋅ b). Perkalian skalar dapat dikeluarkan dari perkalian dot.
- Ortogonalitas: Jika a dan b ortogonal (tegak lurus), maka a ⋅ b = 0.
- Panjang Vektor: a ⋅ a = |a|2. Perkalian dot vektor dengan dirinya sendiri sama dengan kuadrat panjang vektor.
Menghitung Sudut Antara Dua Vektor
Salah satu aplikasi penting dari perkalian dot vektor adalah menghitung sudut antara dua vektor. Dengan menggunakan rumus perkalian dot vektor, kita dapat memperoleh sudut θ antara vektor a dan b sebagai berikut:
cos θ = (a ⋅ b) / (|a| |b|)
Dengan mengetahui perkalian dot vektor a ⋅ b dan panjang vektor a dan b, kita dapat menghitung cos θ. Kemudian, kita dapat menggunakan fungsi arccosine (cos-1) untuk mencari sudut θ.
Misalnya, jika a = (3, 4) dan b = (1, 2), maka a ⋅ b = 3√5, |a| = 5, dan |b| = √5. Jadi, cos θ = (3√5) / (5√5) = 3/5. Oleh karena itu, θ = cos-1(3/5) ≈ 53.13°.
Perkalian Cross Vektor

Perkalian cross vektor merupakan operasi aljabar vektor yang menghasilkan vektor baru yang tegak lurus terhadap kedua vektor awal. Hasil perkalian cross vektor ini sering disebut sebagai “vektor perkalian silang” atau “vektor normal”. Perkalian cross vektor memiliki banyak aplikasi dalam fisika dan matematika, terutama dalam menghitung momen torsi, gaya magnetik, dan dalam menentukan luas bidang paralelogram.
Pengertian Perkalian Cross Vektor
Perkalian cross vektor didefinisikan sebagai operasi yang menghasilkan vektor baru yang tegak lurus terhadap kedua vektor awal. Arah vektor baru ini ditentukan oleh aturan tangan kanan, yaitu jika jari-jari telunjuk dan jari tengah tangan kanan menunjuk ke arah vektor pertama dan kedua, maka ibu jari akan menunjuk ke arah vektor hasil perkalian cross. Besarnya vektor baru ini sama dengan luas paralelogram yang dibentuk oleh kedua vektor awal.
Contoh ilustrasi:
Misalnya, jika kita memiliki dua vektor, a dan b, maka perkalian cross vektornya didefinisikan sebagai:
a × b = |a| |b| sin θ n
Dimana:
– |a| dan |b| adalah besarnya vektor a dan b.
– θ adalah sudut antara vektor a dan b.
– n adalah vektor satuan yang tegak lurus terhadap bidang yang dibentuk oleh a dan b, arahnya ditentukan oleh aturan tangan kanan.
Ilustrasi ini menunjukkan bahwa hasil perkalian cross vektor adalah vektor baru yang tegak lurus terhadap bidang yang dibentuk oleh kedua vektor awal. Besarnya vektor baru ini sebanding dengan luas paralelogram yang dibentuk oleh kedua vektor awal.
Sifat-sifat Perkalian Cross Vektor
Perkalian cross vektor memiliki beberapa sifat penting, antara lain:
- Tidak komutatif: a × b ≠ b × a. Perkalian cross vektor tidak komutatif, artinya urutan vektor dalam perkalian cross mempengaruhi hasil.
- Distributif terhadap penjumlahan: a × (b + c) = a × b + a × c. Perkalian cross vektor distributif terhadap penjumlahan vektor.
- Skoalar perkalian: (ka) × b = a × (kb) = k(a × b). Perkalian cross vektor bersifat komutatif terhadap perkalian skalar.
- Hasilnya adalah vektor nol: a × a = 0. Perkalian cross vektor dari suatu vektor dengan dirinya sendiri menghasilkan vektor nol.
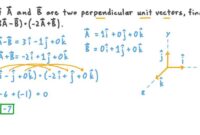
Menentukan Vektor Tegak Lurus dengan Perkalian Cross Vektor
Perkalian cross vektor dapat digunakan untuk menentukan vektor yang tegak lurus terhadap dua vektor lain. Vektor hasil perkalian cross vektor selalu tegak lurus terhadap kedua vektor awal. Untuk menentukan vektor tegak lurus terhadap dua vektor lain, kita dapat melakukan perkalian cross vektor antara kedua vektor tersebut.
Contoh:
Misalnya, kita ingin menentukan vektor yang tegak lurus terhadap vektor a = (1, 2, 3) dan b = (4, 5, 6). Kita dapat melakukan perkalian cross vektor antara kedua vektor tersebut:
a × b = (2 × 6 – 3 × 5, 3 × 4 – 1 × 6, 1 × 5 – 2 × 4) = (-3, 6, -3)
Vektor (-3, 6, -3) adalah vektor yang tegak lurus terhadap vektor a dan b.
Dalam contoh ini, kita telah menemukan vektor yang tegak lurus terhadap kedua vektor awal dengan menggunakan perkalian cross vektor. Vektor hasil perkalian cross vektor selalu tegak lurus terhadap kedua vektor awal, sehingga dapat digunakan untuk menentukan vektor normal terhadap bidang yang dibentuk oleh kedua vektor tersebut.
Penerapan Vektor dalam Geometri

Vektor memiliki peran penting dalam geometri, terutama dalam menentukan posisi, arah, dan jarak. Vektor memungkinkan kita untuk memahami dan menyelesaikan masalah geometri dengan cara yang lebih mudah dan sistematis. Dalam geometri, vektor digunakan untuk menentukan persamaan garis lurus, persamaan bidang, serta menghitung jarak titik ke garis dan jarak titik ke bidang.
Persamaan Garis Lurus dalam Bentuk Vektor
Persamaan garis lurus dalam bentuk vektor dapat ditentukan dengan menggunakan dua informasi utama: titik yang dilalui oleh garis dan vektor arah garis. Berikut langkah-langkahnya:
- Misalkan titik yang dilalui oleh garis adalah titik A dengan vektor posisi a.
- Misalkan vektor arah garis adalah v.
- Maka, persamaan garis lurus dalam bentuk vektor dapat ditulis sebagai: r = a + tv, di mana t adalah parameter skalar.
Persamaan ini menunjukkan bahwa setiap titik r pada garis dapat diperoleh dengan menambahkan ketiganya vektor posisi a dengan kelipatan skalar t dari vektor arah v.
Persamaan Bidang dalam Bentuk Vektor
Persamaan bidang dalam bentuk vektor dapat ditentukan dengan menggunakan titik yang terletak pada bidang dan vektor normal bidang. Berikut langkah-langkahnya:
- Misalkan titik yang terletak pada bidang adalah titik A dengan vektor posisi a.
- Misalkan vektor normal bidang adalah n.
- Maka, persamaan bidang dalam bentuk vektor dapat ditulis sebagai: n · (r – a) = 0, di mana r adalah vektor posisi titik sembarang pada bidang.
Persamaan ini menunjukkan bahwa vektor normal n tegak lurus terhadap setiap vektor yang menghubungkan titik A dengan titik sembarang r pada bidang.
Jarak Titik ke Garis
Untuk menentukan jarak titik ke garis, kita dapat menggunakan konsep proyeksi vektor. Berikut langkah-langkahnya:
- Misalkan titik yang ingin dicari jaraknya adalah titik P dengan vektor posisi p.
- Misalkan garis lurus yang ingin dicari jaraknya ditentukan oleh titik A dengan vektor posisi a dan vektor arah v.
- Hitung proyeksi vektor p – a pada vektor v: projv(p – a) = ((p – a) · v) / ||v||² * v.
- Jarak titik P ke garis adalah panjang vektor p – a – projv(p – a).
Jarak Titik ke Bidang
Untuk menentukan jarak titik ke bidang, kita dapat menggunakan konsep proyeksi vektor. Berikut langkah-langkahnya:
- Misalkan titik yang ingin dicari jaraknya adalah titik P dengan vektor posisi p.
- Misalkan bidang yang ingin dicari jaraknya ditentukan oleh titik A dengan vektor posisi a dan vektor normal n.
- Hitung proyeksi vektor p – a pada vektor n: projn(p – a) = ((p – a) · n) / ||n||² * n.
- Jarak titik P ke bidang adalah panjang vektor projn(p – a).
Penutup
Vektor Matematika Kelas 11 membuka pintu menuju pemahaman yang lebih dalam tentang konsep-konsep matematis yang kompleks. Dengan mempelajari vektor, kita dapat mengaplikasikannya dalam berbagai bidang, mulai dari desain grafis hingga simulasi komputer. Jadi, bersiaplah untuk menjelajahi dunia vektor yang menarik dan penuh tantangan!